指数函数背景创设,复合函数情境应用

顾 艳

江苏省宜兴中学

与指数函数有关的复合函数是指结合指数函数的概念、基本知识与简单函数(一次函数、二次函数等)复合而成的新函数.解决与指数函数有关的复合函数情境应用问题,通常借助函数的解析式、相关概念、基本性质、函数图象等,结合相关的思维技巧,合理转化,巧妙变换,将复杂的复合函数问题简单化,从而实现问题的分析与解决,提升学生的思维能力.

1 性质问题

1.1 函数的单调性

分析：根据题意,对指数进行整体化处理,合理构建函数,通过对应二次函数的配方处理,先确定二次函数的单调性,进而确定单调区间,再结合指数函数的单调性与复合函数单调性的规律解决问题.

解析：令t=x2-2x-1,则函数t=(x-1)2-2在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.

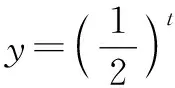
故填答案:(-∞,1).

点评：复合函数的单调性可以利用复合函数的内、外层函数的不同单调性情况,概括为“同增异减”这一基本规律.特别要注意的是,在解决复合函数的单调性问题时,一定要注意“定义域优先”的基本原则,同时熟练掌握基本初等函数的单调性,在相应的定义域内加以分析与讨论.

1.2 函数的值域

A.(0,16] B.[16,+∞)

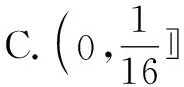
分析：根据题意,对指数进行整体化处理,引入参数构建二次函数,并通过配方处理确定二次函数的值域;结合指数函数的定义域、函数的图象与性质,利用复合函数的基本性质来分析与处理.

解析：设u=x2-6x+5,且u=x2-6x+5=(x-3)2-4≥-4.

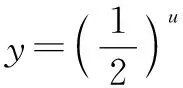
故选:A.

点评：通过分解复合函数,利用内、外层函数之间的关系,结合内层函数的解析式确定其值域,再通过“由内到外”来求解相应的值域即可.在解决指数函数背景下的复合函数的值域或最值问题时,可以按照“由内到外”的顺序研究复合函数的内函数值域A与外函数定义域B之间的关系,保证内函数值域A是外函数定义域B的子集,再结合条件中相关函数的单调性等性质加以分析与求解.

2 常数问题

例3已知函数f(x)=aex2-1-1,a为常数,若函数y=f(x)的最小值为0,则实数a的值为______.

分析：根据题意,对指数进行整体化处理,引入参数构建二次函数,进而确定二次函数的单调性与单调区间;结合指数函数的单调性,利用复合函数的基本性质,分别讨论a=0,a<0和a>0时对应函数的单调性与单调区间;结合题设条件进行分析,进而构建函数最小值的关系式,得以确定对应的实数a的值.

解析：设u=x2-1,则函数u=x2-1在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增.

又指数函数y=eu是R上的增函数,所以分类讨论如下.

当a=0时,可得f(x)=-1恒成立,不符合题意,舍去.

当a<0时,结合复合函数的单调性,可知函数f(x)=aex2-1-1在区间(-∞,0)上单调递增,在区间(0,+∞)上单调递减,此时函数f(x)在x=0处有最大值,无最小值,不符合题意,舍去.

综上所述,函数y=f(x)最小值为0时,a=e.

故填答案:e.

点评：抓住常数的不同取值情况以及常数与复合函数的关系进行分类讨论,利用常数的正负取值情况对复合函数在不同区间上的单调性的影响,结合相关的概念与基本知识加以综合与应用.熟练掌握复合函数的单调性以及基本初等函数的基本性质,是破解此类综合应用问题的关键.

3 应用性问题

表1

(1)求y关于x的函数关系式y=f(x);

(2)求函数f(x)的最大值.

分析：根据情境内容,通过分类讨论,在自变量不同的取值情况下,结合对应的函数类型利用待定系数法求解,得以确定对应的函数关系式,并利用不同变量取值情况下,二次函数的最值以及指数型函数背景下复合函数的最值情况,得以确定函数的最大值.

解析：(1)当0≤x<6时,由题意,设f(x)=ax2+bx+c(a≠0),由题中表格数据可得

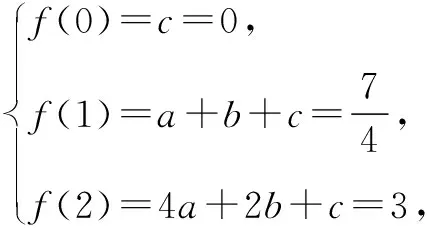
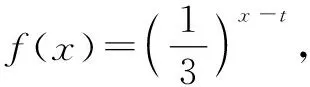
综上,y关于x的函数关系式为

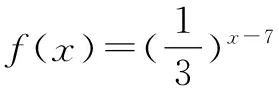
而4>3,所以函数f(x)的最大值为4.

点评：在解决涉及复合函数中的应用性问题时,关键是借助对相关文字内容的理解,合理构建数学中的相关模型,为问题的进一步综合与应用提供条件.研究分段函数背景下的最值问题,要分别讨论自变量在不同取值范围下对应函数的最值或取值范围情况,然后加以综合.

复合函数情境应用与创新应用问题是高中数学中的一个知识交汇点与融合点,也是一个重点与难点,是每年新高考数学试卷中必考的重点基本内容之一.借助指数函数背景来创设相应的复合函数情境,结合指数函数自身的特点与性质,并综合复合函数的相关知识,渗透相关的数学思想方法,构建数学知识网络体系,优化数学解题思维,提升数学解题能力,全面培养数学核心素养.