弹载SINS/GPS组合自对准方法

屈新芬,李世玲,祝 刚,王启明

(中国工程物理研究院电子工程研究所,四川 绵阳 621900)

0 引言

中低精度SINS/GPS组合系统在无参考角度、无转位机构或速度信息辅助的地面静态或动态发射场景下,方位角自对准误差将达到数度至数十度甚至更大,大失准角下后续必须采用非线性滤波算法在载体飞行动态下对姿态角误差进行估计与修正[1-2],而非线性滤波计算量大,不能满足实时性要求较高的场景,过大的失准角还将导致非线性滤波算法发散。空中飞行载体在SINS/GPS组合系统发生故障、发射段高过载冲击等都需SINS/GPS组合在空中动态下加电启动并完成飞行中的满足一定精度要求的初始自对准,以满足后续SINS/GPS组合线性滤波甚至较长时间丢星下纯惯性工作精度的要求。

针对上述问题,国内外学者开展了多种动态对准方法。文献[3-5]为基于载体小侧滑角和小攻角方法。文献[6-7]分别利用单矢量迭代求解方法于双矢量实现粗对准,单/双矢量迭代算法对准精度受载体动态和冲击影响大。文献[8] 通过构建积分多矢量并采用Request 算法,在积分多矢量构建中反复使用测量数据。近年来基于惯性系惯导自对准方法在舰载、车载、机载等动态场景或晃动场景得到了一定的工程应用[9-17],但其在弹载等大动态场景的应用尚少。本文将基于惯性系动态初始对准方法引入弹载SINS/GPS初始对准中,剖析大动态场景下影响姿态角对准精度的主要因素,提出用大动态特征值实现对准开始时间与结束时间的自动辅助判断策略。

1 惯性系初始对准算法理论基础

1.1 惯性系初始对准原理

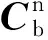
(1)

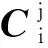
(2)

(3)

式中,

其中,ωie为地球自转角速度,上标T表示转置。

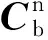
1.2 Wahba问题与求解方法

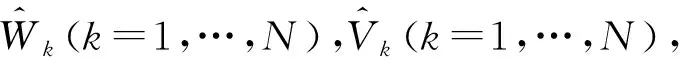
(4)

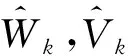
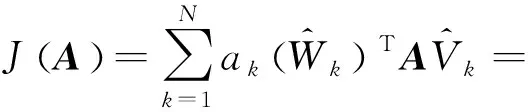
(5)

式(5)中,ak为最小二乘系数,工程上常取为1;tr( )表示对矩阵求迹。

Wahba问题常用经典求解方法是SVD(singular value decomposition)算法与QUEST(quaternion estimator)算法。两种算法理论上等价,都充分利用尽可能多的信息,计算量相当,在本文给定动态下仿真效果相同,算法可参考文献[14-17]。

2 SINS/GPS组合自对准算法

2.1 SINS/GPS组合动态自对准算法

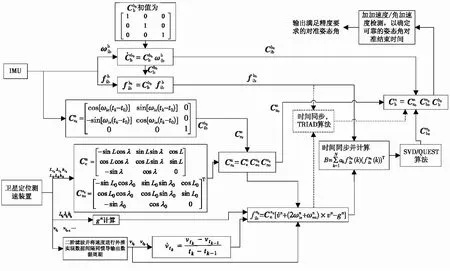
图1 INS/GPS初始对准算法结构图Fig.1 INS/GPS self-alignment algorithm configuration

(6)

(7)

2.2 误差分析与对准启动与结束时间点的自动判断

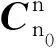
(8)

(9)

(10)

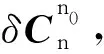
(11)

综上,载体速度、加速度大小及测量精度、角速度大小及测量精度、载体测量速度的时间微分误差及速度测量精度是影响初始对准精度的主要因素。较之于低动态,大动态环境下SINS内各传感器标度因数误差和安装误差引起的角速度和加速度测量误差大很多。因此设置加速度和角速度门限和持续时间,当加速度和角速度绝对值及变化率小于设置门限且持续时间大于设定时间时,即式(12)条件同时满足才启动初始对准并记录启动时间点tq;同理在初始对准时长大于设定最短对准时间长度且加速度和角速度及变化率绝对值小于设置门限值即式(13)条件同时满足才结束初始对准。

(12)

式(12)中,fset1,ωset1,Δfset1,Δωset1分别为初始对准启动加速度与角速度及变化率(由相邻采样值之差除以采样间隔时间得到)门限;t0,tk,tset1分别为载体起飞时间点、当前时间点和预设的初始对准启动点距起飞点时间长度;Δfset1,Δωset1,tset1根据具体的设计轨迹动态进行粗略设计。

(13)

式(13)中,fset2,ωset2,Δfset2,Δωset2分别为初始对准结束加速度与角速度及变化率门限,tset2为最小初始对准时长设定值,nset2为初始对准结束前加速度和角速度及变化率小于设定值的持续时间最小采样次数设定值,这些门限值可以根据具体的设计轨迹动态进行粗略设计。n为初始对准启动后连续满足式(13)前5个方程的角速度加速度连续采样次数。

3 试验与测试验证

为验证本文算法对大动态环境的有效性与适应性,设计搭载试验进行考核。该飞行前段即起飞点至飞行30 s之内,最大加速度与加加速度达到196 m/s2,980 m/s2以上,最大角速度与角加速度达到220 (°)/s和1 000 (°)/s2以上,试验飞行80 s附近设计约8 s时长幅值大于40 (°)/s的滚转角速度运动,试验飞行110～130 s时间段内滚转角速度最大值达60 (°)/s以上。

飞行试验配置光纤陀螺惯组和GPS接收机,陀螺和加速度计零偏稳定性、重复性为1 (°)/h,0.001g水平,标度因数误差都为0.01%水平,SINS,GPS输出数据频率分别为200 Hz和10 Hz。试验搭载DSP+FPGA嵌入式计算机内采用大动态特征值决策辅助的SVD算法,即当加速度和角速度绝对值小于设置门限且持续时间大于设定值时(fset1,Δfset1,ωset1,Δωset1,tset1分别取12 m/s2,100 m/s3,5 (°)/s,100 (°)/ s2,40 s),才启动初始对准;在启动初始对准后,加速度和角速度绝对值小于设置门限且持续时间大于设定值时(fset2,Δfset2,ωset2,Δωset2,tset2分别取12 m/s2,100 m/s3,5 (°)/s,100 (°)/ s2,200 s)时输出姿态角,本文为方便查看,将不同时间下初始对准精度将tset2设置为0。姿态角对准精度的评判基准为飞行全程工作的惯性/GPS组合系统,用对准输出姿态角减去基于地面方位角装订的全程工作惯性/GPS组合系统的姿态角所得结果如图2(a)。对飞行试验回收SINS数据和GPS数据分别采用TRIAD积分算法和SVD算法进行解算,TRIAD积分算法的初始对准开始时间依次从载体起飞时间点开始每间隔1 s往后移动,且每组对准时长都设为100 s,姿态角对准误差见图2(b);SVD算法初始对准启动开始时间为载体起飞点,启动后姿态角对准误差时间关系见图2(c)和图2(d)。

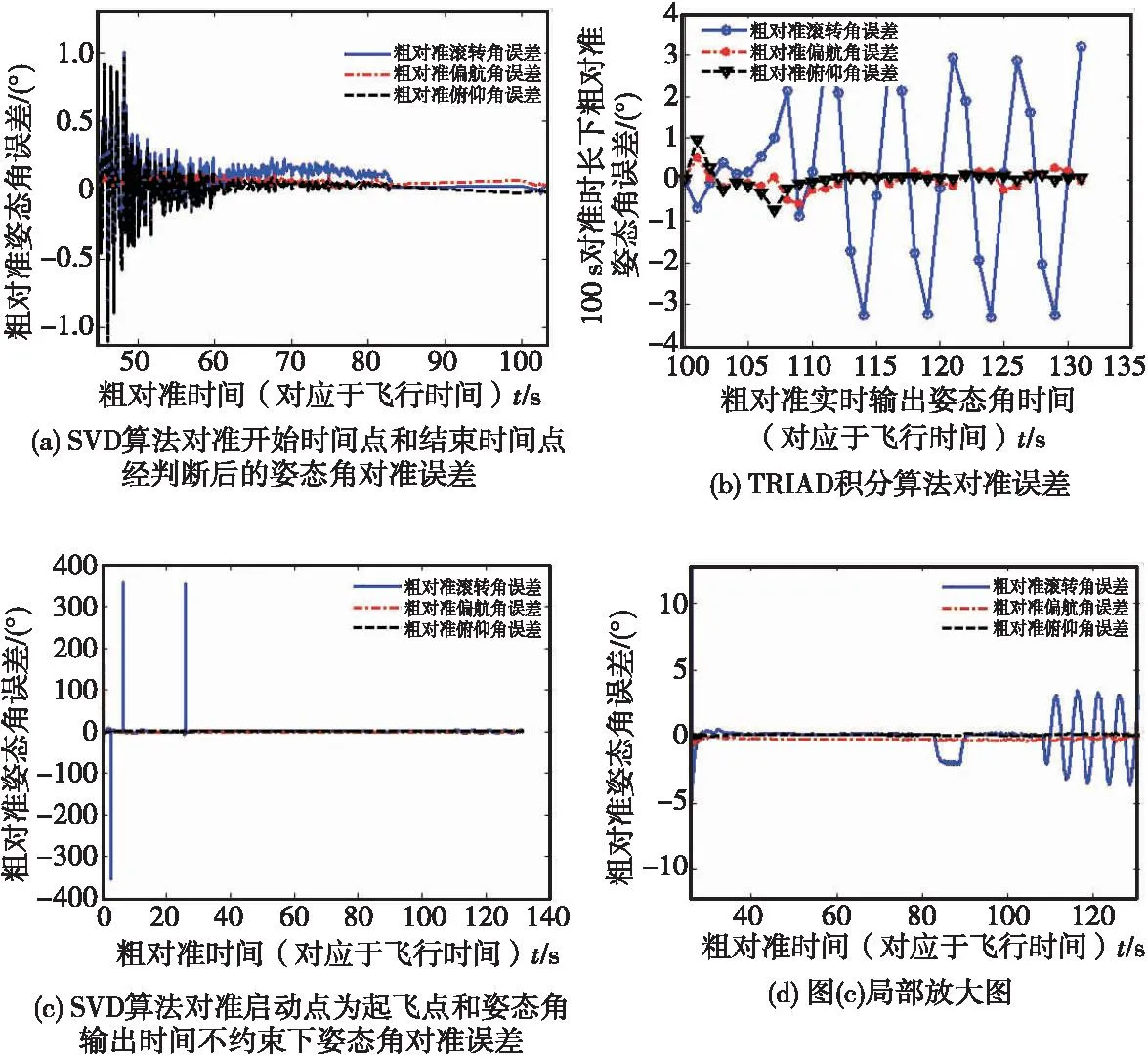
图2 飞行全程下对准姿态角误差Fig.2 Alignment attitude error in flight

在不采用大动态特征值决策辅助的图2(c)、图2(d)中,在起飞至飞行30 s、试验飞行80 s附近和试验飞行110～130 s时间段,因存在大角速度、大加速度、大角加速度或大加加速度及其耦合影响,在大动态时间段内SVD算法实时对准姿态角误差很大甚至达到上百度,且在这些大动态之外的平稳飞行段的三个姿态角实时对准误差最大值也达到-2.3°甚至更大误差值;而采用大动态特征值决策辅助的图2(a)结果中,SVD算法输出的姿态角对准误差较小,在飞行55 s后姿态角对准误差最大值小于0.2°,满足SINS/GPS组合线性滤波与较短时间工作的纯惯性初始对准精度的要求。采用TRIAD积分算法的图2(b)结果中,姿态角对准误差较大,除受对准时长的影响外,还与对准起始点的选择有关,不方便弹载飞行环境的工程应用。

为考察不同精度惯组下SVD算法的对准精度,对飞行试验所设计的标称六自由度数据采用大动态特征值决策辅助SVD算法进行仿真,并在此基础上分别叠加惯性测量误差(第1组设置陀螺与加速度计零偏稳定性(1σ)和重复性(1σ)分别为0.01 (°)/h,0.000 01 m/s2,非线性都为0.001%;第2组为1 (°)/h,0.001 m/s2,0.01%;第3组为10 (°)/h,0.005 m/s2,0.03%)进行50条蒙特卡洛仿真,对准时长取100 s,仿真统计结果见表1。表1中δφ,δγ,δθ分别表示对准滚转角误差、方位角误差和俯仰角误差。

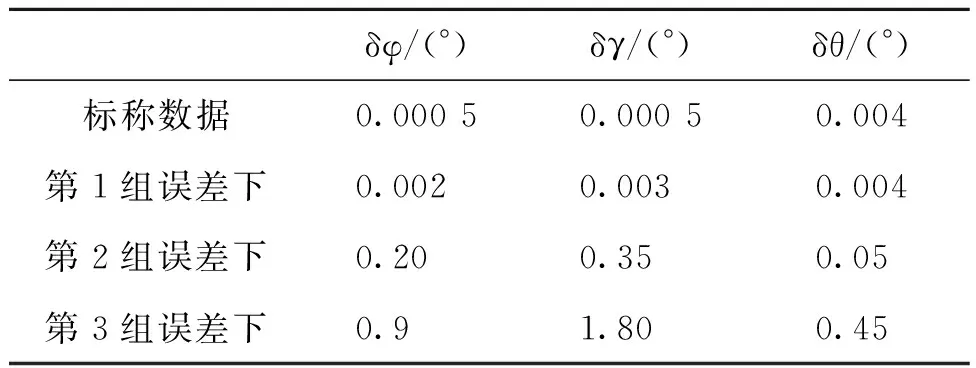
表1 标称数据与三种精度惯导下动态对准误差Tab.1 Standard data and alignment errors with the three different precision IMU

由表1知,试验动态下,当SINS的陀螺与加速度计零偏稳定性、重复性、标度因数误差分别为1 (°)/h,0.01 m/s2,0.01%或更高精度时,姿态角动态对准精度优于0.35°(1σ),与图2(a)解算结果精度相吻合;陀螺与加速度计相应误差分别为10 (°)/h,0.05 m/s2,0.03%下,姿态角动态对准精度优于1.8°(1σ)。

4 结论

本文将惯性系的最优初始对准SVD和TRIAD算法引入大动态场景,在分析姿态角动态对准误差影响因素基础上,通过飞行试验、回收数据离线测试和标称理想数据仿真,得到以下结论:

1) 本文提出的大动态特征值决策辅助SVD姿态角对准算法根据载体动态对对准启动点和对准结束点进行在线调整,提高了过程机动下姿态角对准精度;

2) 大动态场景,基于TRIAD算法的姿态角对准误差除受对准时长的影响外,还与对准起始点的选择有关,过程机动下姿态角对准精度难保证;

3) 惯组精度直接影响动态姿态角对准精度,惯组精度越高,姿态角对准精度越高。