基于改进自适应扩展卡尔曼滤波的高精度姿态解算

吴叶丽,行鸿彦,侯天浩,王海峰,李 瑾

(南京信息工程大学电子与信息工程学院,江苏 南京 210044)

0 引言

高精度姿态角度解算对移动目标自主定位导航有着重要的应用价值[1-3]。姿态角度可以通过陀螺仪传感器[4]的积分得到,但是所测数据在长时间积分环境下容易产生累积误差,单个的传感器采集到的数据信息较为单一,不具有可靠性,并且进行姿态解算的过程中,传感器采集的数据中会存在不确定性的系统噪声和测量噪声,导致得到的位姿结果产生较大的偏差。而采用陀螺仪传感器、加速度传感器和地磁计对姿态变换情况共同进行跟踪可有效解决上述问题,确保采集的数据具有充分性和可靠性,通过将三个传感器的数据进行信息融合,实现较为准确的姿态估算。

国内外学者对多个应用背景下的姿态解算进行了大量研究[5-7]。文献[8]提出一种结合共轭梯度法和互补滤波的混合滤波算法,实现惯性传感器的姿态解算,但没有充分考虑传感器数据的影响、算法迭代复杂且计算量较大。文献[9]通过对多个惯性传感器进行空间阵列布局,并设计了基于BP神经网络的误差补偿模型,减少姿态的误差,一定程度上提高了姿态解算的准确性,但该方法姿态解算过程中增加了较多计算参数,解算实现步骤较为复杂。文献[10]提出了一种基于优化自适应无迹卡尔曼滤波的姿态解算方法,通过对陀螺仪数据和加速度数据进行误差预处理,再通过所提算法实现姿态角度解算,但在滤波过程中没有考虑误差的迭代更新过程。文献[11]提出了一种基于Q学习的方法,可以自动调整过程和测量噪声协方差矩阵的值,解决了迭代过程中的误差影响,降低了姿态解算误差,但同时更新过程和测量噪声协方差矩阵和容易造成姿态发散且计算量增加。文献[12]将互补滤波器与EKF算法相结合,提出了一种改进的EKF滤波算法实现对无人机的姿态解算,一定程度上提高了精度和实时性,但是该方法需要进行两步滤波过程,计算量大且容易导致结果发散,仍需要对解算精度进行提高。

为解决已有方法的姿态解算精度较低和计算复杂等问题,本文通过设置权重值对测量噪声协方差矩阵R的估计公式进行改进,提出一种改进加权自适应的扩展卡尔曼滤波算法应用于姿态解算。

1 优化自适应的扩展卡尔曼滤波算法

传统的EKF模型要求过程噪声和测量噪声的均值为零且统计特性已知的白噪声。但在动态实践中无法满足上述要求,也无法准确地对噪声的统计特性进行描述。Sage-Husa自适应滤波方法可有效顾及实际过程中的测量信息和动态信息,可以不以动力学模型噪声先验协方差矩阵为基础,就能估计出状态向量和测量向量的协方差矩阵,可有效进行滤波。

1.1 Sage-Husa自适应滤波算法

Sage-Husa滤波利用开窗法估计出此刻的测量噪声协方差矩阵或过程噪声协方差矩阵,使过程噪声协方差矩阵和测量噪声协方差矩阵自适应于此时的状态信息和测量信息,结合EKF滤波进行解算,进而获得最优的状态估计值。

EKF的非线性系统表达式为

(1)

对于非线性的EKF系统线性化后其系统方程为

(2)

式(2)中,X(k)为状态向量;Z(k)为观测向量;A为状态转移矩阵,是状态向量非线性函数泰勒级数展开式的一阶项;H为观测矩阵;w(k)为过程噪声;v(k)为测量噪声。

由上,基于Sage-Husa的时变噪声统计估计器[13]为

q(k)=(1-d(k))q(k-1)+
d(k)(X(k|k)-AX(k-1|k-1)),

(3)

Q(k)=(1-d(k))Q(k-1)+d(k)(K(k)ε(k)·
ε(k)TK(k)T+P(k|k)-AP(k-1|k-1)AT),

(4)

r(k)=(1-d(k))r(k-1)+d(k)(Z(k)-
HX(k|k-1)),

(5)

R(k)=(1-d(k))R(k-1)+d(k)(ε(k)ε(k)T-
HP(k|k-1)HT),

(6)

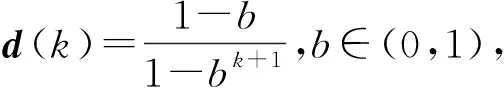
但传统的Sage-Husa自适应滤波方法存在一些缺点:

1) 由文献[14]可知,在实践过程中不能同时估计出系统中的Q和R,只能在一方已知的条件下,估计出另一个;

2) 由式(3)-式(6)可知,d(k)和b的数值选取,直接影响了系统的自适应程度,传统的Sage-Husa自适应方法,使用单一的d(k)数值对不同传感器测得的数据进行噪声估计,不能满足实际的要求,容易产生较大的误差;

3) 由式(4)、式(6)可知,系统的噪声方差矩阵Q或R可能失去半正定性和正定性发生滤波发散,导致系统不具有稳定性和收敛性。因此,本文需要针对上述问题对传统的Sage-Husa自适应滤波方法进行改进。

1.2 优化加权自适应的扩展卡尔曼滤波算法

针对在实践过程中不能同时估计出系统中的Q和R的问题,本文实现姿态解算的系统的过程噪声较小并且变化较为稳定,而噪声通常受到复杂的环境影响,使得实际过程中的测量噪声会发生较大的变化。因此,本文仅对系统的测量噪声协方差R进行估计,对过程噪声协方差矩阵Q设置为已知定值,并且对测量噪声协方差矩阵进行改进,提高系统的稳定性和准确性。由此,本文提出一种改进的加权Sage-Husa自适应扩展卡尔曼滤波算法。算法流程如下:

状态预测方程:

X(k|k-1)=f(X(k-1|k-1))。

(7)

预测协方差方程:

P(k|k-1)=AP(k-1|k-1)AT+Q。

(8)

更新增益方程:

K(k)=P(k|k-1)HT[HP(k|k-1)HT+R]-1。

(9)

计算残差:

e(k)=Z(k)-g(X(k|k-1))。

(10)

更新状态估计方程:

X(k|k)=X(k|k-1)+K(k)e(k)。

(11)

更新协方差矩阵方程:

P(k|k)=(I-K(k)H)P(k|k-1)。

(12)

对不同的传感器的噪声统计特性的置信程度进行判断,对不同传感器测量所得的数据赋不同的权重值,可以有效解决单一的d(k)数值对不同传感器测得的数据进行噪声估计而导致产生误差的问题。

滤波出现收敛趋势时,误差协方差矩阵P逐渐减小至0,可忽略不计,对传统的测量噪声协方差矩阵R的估计公式进行改进,保留残差e(k),同时使其满足传统R的变化趋势,保证了矩阵R的正定性,防止发生滤波发散的情况,使R随着噪声和系统真实情况的变换进行估计。

改进的加权测量噪声协方差矩阵更新方程:

R(k)=(I-w(k)D(k))R(k-1)+w(k)D(k)·
|((I-HK(k-1))e(k)e(k)T(I-HK(k-1))T)|,

(13)

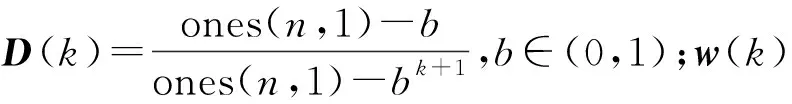
综上所述,改进算法结构简单、计算效率高、稳定性好、灵活性高,更适用于系统求解姿态角度信息。

2 基于优化加权自适应扩展卡尔曼滤波的姿态解算

姿态角一般由陀螺仪、加速度计传感器的测量数据解算得到[15],陀螺仪可由所测角速度经积分得到三个姿态角:俯仰角、航向角和横滚角,其不易受到外界环境的干扰,且短时内的测量值较为准确但单一的陀螺仪测得数据在长时间积分环境下容易产生累积误差,而加速度计和磁力计长时间测量的数据比较稳定、准确。因此,本文利用提出的WAEKF方法将陀螺仪、加速度计和地磁计的测量数据进行了融合,实现对陀螺仪实践过程中产生的随机偏移误差的修正,在EKF算法的基础上,加入自适应过程,控制系统的残差矩阵对系统的影响,进而得到姿态角的最优估计。其实现原理如图1所示。

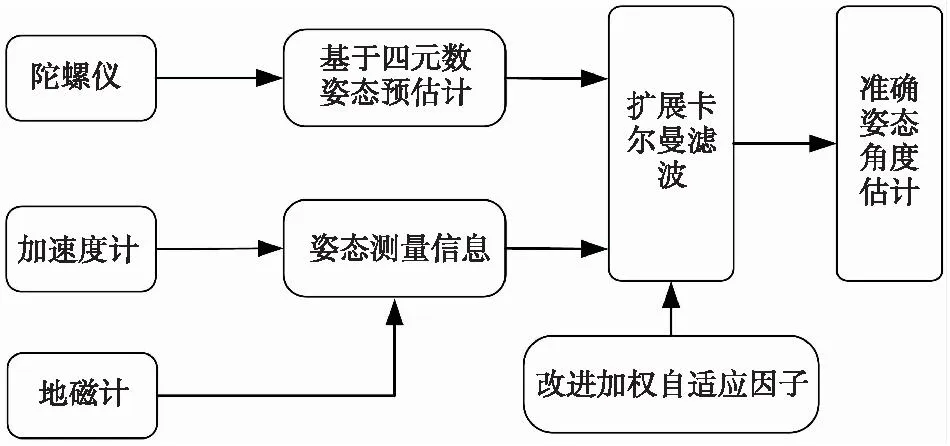
图1 基于改进方法的姿态角度估计原理图Fig.1 Schematic diagram of attitude angle estimation based on the improved method

2.1 基于惯性导航的姿态解算原理

姿态解算的方法主要有欧拉法、方向余弦法和四元数法等。欧拉法的计算速度较慢,并且计算过程中矩阵会产生“奇点”,造成万向节死锁的现象[16],实时计算困难,难以用于实践。方向余弦法可有效避免欧拉法出现的“奇点”现象,但计算量较大、较为复杂。因此本文在姿态融合过程中使用四元数法,可克服欧拉法的缺点并且方法简单、计算量较小。最终将四元数转换为欧拉角,得到姿态角信息。

若载体坐标系为B系,地理坐标系为N系,两者可通过旋转矩阵进行转换,由四元数表示的从地理坐标系旋转到载体坐标系的旋转矩阵[17]为

(14)

则由旋转矩阵解算出目标载体的欧拉角,即俯仰角γ、横滚角θ和航向角φ为

(15)

2.2 基于惯导和改进方法的姿态解算

基于惯导系统和四元数法构建状态方程和测量方程,将四元数和陀螺仪角速度偏移量作为状态方程的变量,将加速度计和地磁计测得的数据作为测量信息,加入自适应因子考虑系统的测量噪声对系统精度的影响,提高系统姿态角最优估计的准确性。

2.2.1建立状态方程

使用一阶龙格-库塔法对陀螺仪的角速度值进行更新处理,实现四元数值的更新,则由龙格-库塔法得到的离散模型[18]为

(16)

式(16)中,q(k),q(k-1)分别为k,k-1时刻的四元数;T为系统采样时间间隔;ΩB为载体坐标系相对于地理坐标系的角速度在载体坐标系上的分量。

陀螺仪的偏移量模型可表示为

(18)

则,以四元数和陀螺仪数据偏移量作为状态变量,进而建立的状态方程为

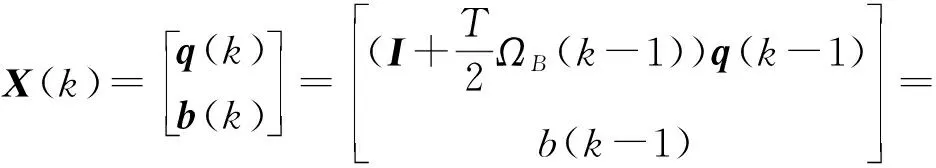
(19)

2.2.2建立测量方程

本文将加速度计和地磁计得到的数据作为测量方程,对状态向量实现补偿估计,设加速度计数据为aB,地磁计所测数据为mB,与地理坐标系中的加速度和磁场mN关系[19]可表示为

(20)

通过地磁和加速度计解算所得的姿态角经过求解得到初始四元数的数值,进而实现四元数的更新优化,由式(20)求解可得由地磁计和加速度计数值表示的姿态角的表达方式为

(21)

选取加速度计和地磁计的数据向量作为测量信息,因此本系统的测量方程表达式为

(22)

2.2.3姿态估计的实现步骤

本文改进WAEKF方法可以更新时变噪声矩阵参数R,因此,通过本文方法实现姿态角度解算,可有效解决姿态解算过程中的误差累积问题,提高姿态解算精度。将地磁计的测量数据、加速度传感器的测量数据和陀螺仪传感器的测量数据经本文方法解算处理后,得到最优姿态。

算法具体的实现步骤如下:

1) 建立系统的状态方程(19)和测量方程(22),并对系统进行初始化设置;

2) 根据式(7)、式(8)实现时间更新,得到预测状态变量X(k|k-1)和预测协方差矩阵P(k|k-1);

3) 根据式(9)更新滤波增益,利用增益K(k)更新k时刻的最优状态估计X(k|k)和协方差矩阵P(k|k);

4) 重复上述步骤2)至3),实现四元数的最优估计,得到最优姿态角度信息。

本文算法通过使用改进的噪声统计估计器,能够有效避免滤波发散,并且能够实时地估计和修正系统的量测噪声,实现系统的最优估计。

3 实验与结果分析

基于MPU9250搭建移动小车实验平台,将惯性传感器在二维水平面内进行移动,利用算法实现移动小车的姿态融合解算,获取更加准确的姿态信息。基于本文的WAEKF方法实现陀螺仪数据、加速度数据和地磁计数据的姿态解算,并将实验的解算结果与传统AEKF、EM-AEKF和互补滤波方法进行对比分析,验证本文方法求解姿态角具有优越性。

为直观体现改进方法的姿态解算实验效果,本文选取均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)对姿态角度误差情况进行衡量评估[20]。RMSE和MAE表达式如下:

(23)

(24)

式(23)、式(24)中,N表示所测数据个数,x(t)表示系统的解算估计值,y(t)表示系统的真实数据。RMSE可以反映出数据值与真实值之间的拟合程度,RMSE的值越小,表明处理后的实验数据具有更高的精确性。MAE可凸显实验值与真实值之间的数值差距,通过将所有的误差绝对值相加,可以有效避免因数据值比真实值局部过高或过低而抵销误差,因此较适合用于评估数据的整体误差。

3.1 与传统AEKF算法的误差对比

将惯性传感器在二维水平面内进行直线运动。使用AEKF滤波器和本文的WAEKF方法对惯性测量单元数据进行处理,并将实验的解算误差结果进行比较分析,采样周期为0.02 s。

3.1.1传统自适应扩展卡尔曼滤波的角度解算误差实验分析

采用基于传统的Sage-Husa自适应扩展卡尔曼滤波算法对传感器的数据进行融合,分别得到俯仰角、航向角和横滚角的姿态角度信息,并将其与真实值之间的误差情况进行表现,显示出传统算法的融合效果,效果如图2所示。

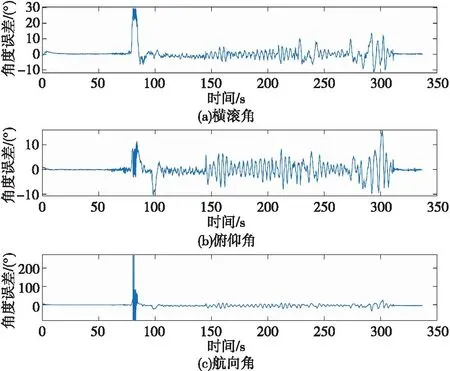
图2 基于AEKF姿态解算角度误差曲线Fig.2 Angle error curve calculated based on AEKF attitude

由图2可看出,基于AEKF的姿态解算结果存在较大误差值。解算的横滚角误差极值差约为40°,在数列值为85 s附近出现误差极大值,高出真实值33°,误差变化较为明显。基于AEKF姿态解算的俯仰角误差波动幅度值约为28°,误差极大值高出实际值18°,误差变化分布的较为明显。基于AEKF解算的航向角的误差值在75～85 s区间外整体变化较为平稳,但在75～85 s区间内出现了异常尖峰误差,误差极值大于200°,对解算结果造成了较大影响。因此,传统的AEKF对惯性传感器数据进行滤波解算后,姿态角度的误差变化情况都较为明显,误差值变化区间较大并且都出现了一段异常尖峰值,因此仍需要对传统的AEKF滤波算法进行改进。

3.1.2优化加权自适应扩展卡尔曼滤波的角度解算误差实验分析

在吸收Sage-Husa滤波和基于传感器置信程度进行加权的基础上,本文提出一种新的WAEKF方法,用于改善传统的AEKF滤波算法的不足,增加滤波融合的灵活性和有效性。

由图3可知,基于WAEKF方法解算的姿态角误差明显小于AEKF的姿态解算结果,能够更加准确、有效地实现姿态解算。WAEKF方法解算的横滚角的误差整体变化较为平缓,无异常尖峰值段,相较于AEKF算法的误差变化范围减小约33°,横滚角误差变化程度有所控制。本文方法解算的俯仰角误差波动幅度值约为13°,误差极大值高出实际值8°,相较于AEKF算法误差极大值减小约10°。基于本文方法得到的航向角误差波动幅度值约为13°,远小于基于AEKF算法的航向角误差数值范围,并且整体误差值偏小。

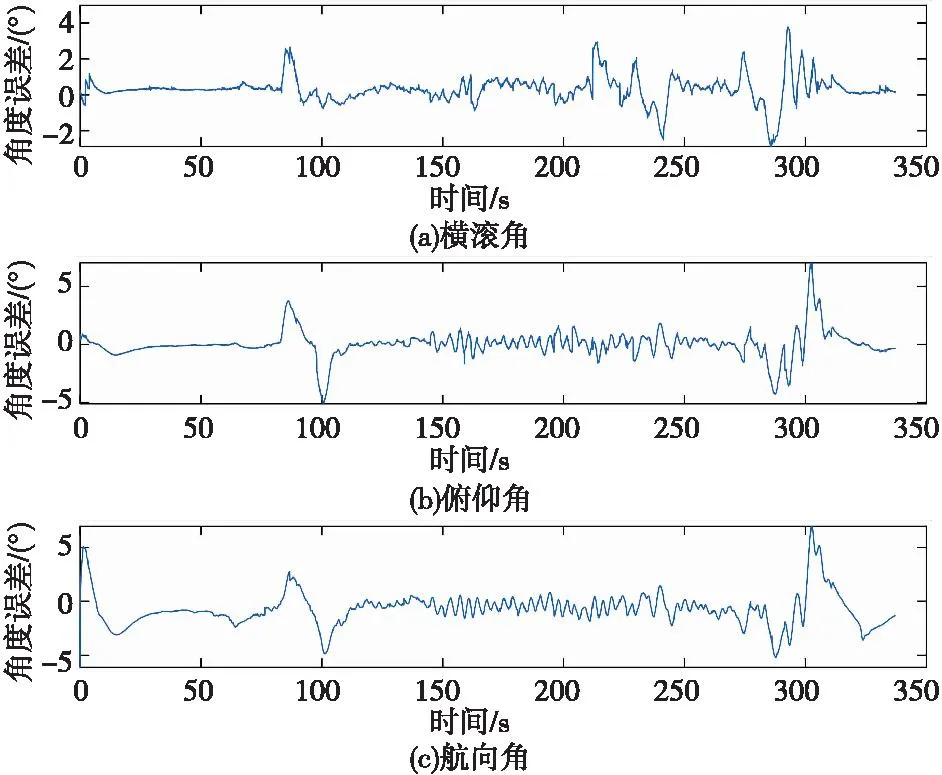
图3 基于WAEKF姿态解算角度误差曲线Fig.3 Angle error curve calculated based on WAEKF attitude

因此,基于WAEKF方法解算的姿态角度信息相较于传统的AEKF算法的解算结果得到了有效地改善,尤其是航向角角度值变化更加准确,说明基于WAEKF方法的姿态解能够依靠改进的测量噪声协方差矩阵自适应滤除噪声,减小误差,提高姿态解算精度。

3.2 姿态角度对比分析

为证明本文方法对姿态角度解算具有高效性,将惯性传感器在二维水平面内进行直线运动。利用互补滤波、基于EM-AEKF和本文的WAEKF方法分别对传感器数据进行处理,直观对比不同方法融合得到的角度变化情况,结果如图4-图6所示。w(k)取(0.5,0.95,0.95,0.95,0.99,0.99)。

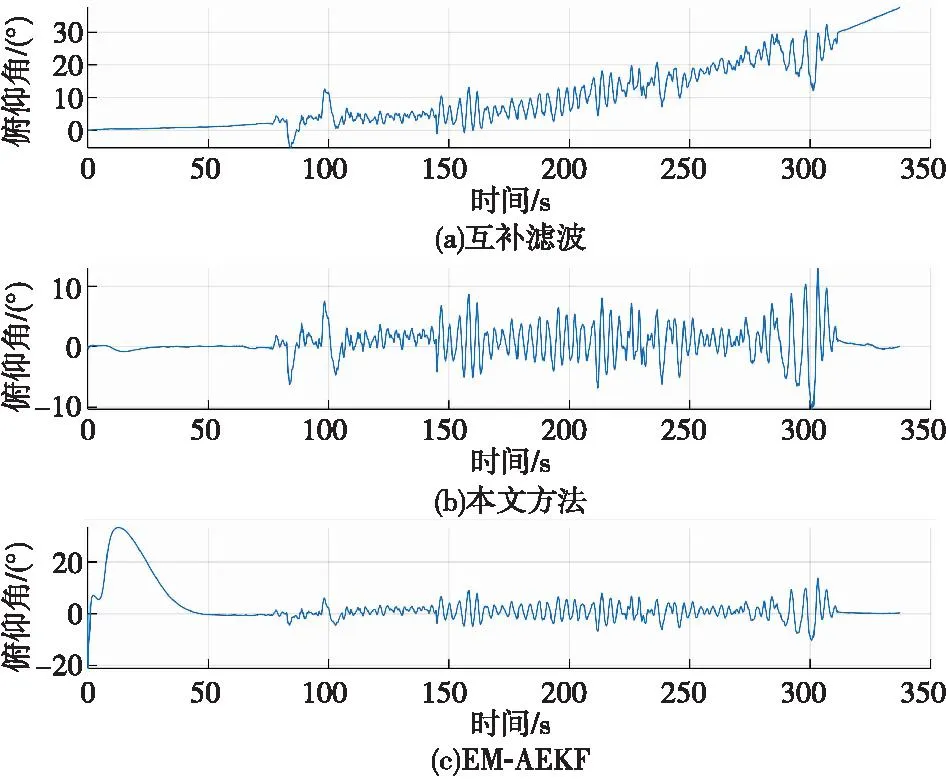
图4 不同方法解算的俯仰角角度变化图Fig.4 Elevation angle variation figure calculated by different methods

由图4可知,互补滤波方法解算后在时间序列200 s后得到的俯仰角随着时间的推移,信号发生严重漂移,误差逐渐增大,因此互补滤波方法较不适合俯仰角的融合解算。基于EM-AEKF方法解算的俯仰角在时间序列为0～50 s内误差较大,误差波动幅度值约为30°,因此该方法解算的俯仰角误差依然较大。基于WAEKF方法融合解算后的俯仰角整体波动最为平缓,误差值相较于互补滤波和基于EM-AEKF方法最小。

由图5可知,基于互补滤波方法解算的横滚角在时间为100 s后逐渐下降低至-55°,互补滤波方法解算的横滚角误差较大。基于EM-AEKF方法解算的横滚角在时间为0～50 s内误差较大,误差极值约为-50°左右,且随着时间的增加,横滚角波动较为明显,因此该方法解算的横滚角存在明显失真。基于WAEKF方法解算的横滚角整体波动稳定,误差波动幅度值约为20°,解算的横滚角误差远小于互补滤波和EM-AEKF方法。

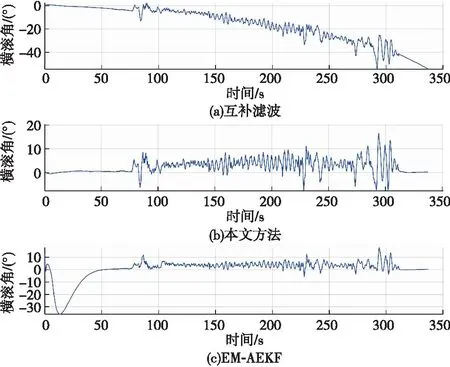
图5 不同方法解算的横滚角角度变化图Fig.5 Changes of roll angle calculated by different methods

由图6可知,基于互补滤波方法在整个时间序列内解算得到航向角的波形呈上升趋势,随着数据的叠加,误差逐渐增大,最大值偏离40°,因此互补滤波方法较为不适合本文数据下的航向角融合。基于EM-AEKF方法解算的航向角整体变化较为稳定,但0～8 s之间存在较大异常值,因此该方法仍待改进。基于WAEKF方法解算得到的航向角角度值在-109°～-94°之间,解算的航向角误差相对最小,角度变化具有稳定性和准确性,因此可以用于实际应用中求解航向角。

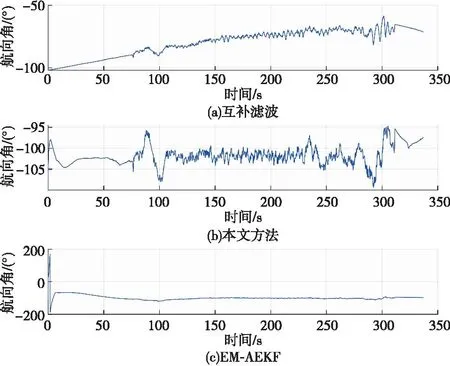
图6 不同方法解算的航向角角度变化图Fig.6 Variation of course angle calculated by different methods

综上所述,基于互补滤波方法解算的俯仰角、横滚角和航向角都存在明显的漂移现象;基于EM-AEKF方法解算的俯仰角、横滚角和航向角都存在较大的异常值。本文的WAEKF方法可有效解决互补滤波方法姿态解算存在漂移和EM-AEKF方法姿态解算存在异常值导致误差较大的问题,WAEKF方法解算的俯仰角、横滚角和航向角波形变化都较为平稳且误差较小,能够提高姿态解算精度,较适用于实践应用。因此,WAEKF方法具有优势性和准确性。

本文为对比四种方法下姿态角的解算效果,使用MAE对其误差进行衡量,并通过记录计算时间衡量四种方法的实现效率,结果如表1所示。

表1 不同方法航向角解算误差对比表Tab.1 Comparison table of heading angle calculation errors of different methods

从表1可知,本文的WAEKF方法解算得到的横滚角的RMSE和MAE值明显小于其他三种方法,EM-AEKF和互补滤波方法解算的横滚角误差较大。WAEKF方法解算的俯仰角的RMSE和MAE明显小于EM-AEKF和互补滤波方法,略小于AEKF方法。基于WAEKF方法解算得到的航向角的RMSE和MAE值明显小于其他三种方法,且相较于AEKF方法,解算得到的航向角的RMSE和MAE分别降低了84.23%,78.28%。

因此,本文的WAEKF方法相较于互补滤波、AEKF和EM-AEKF方法的姿态解算效果最好,误差最小,能够自适应滤除噪声影响,姿态解算精度最高。

为验证本文方法的姿态解算具有适用性,在上述相同实验条件下,将惯性传感器在水平二维平面内进行多角度变化运动,由于本文主要考虑载体在二维水平面内的移动,此时只有航向角发生显著变化,不同方法下的航向角解算结果如图7所示。

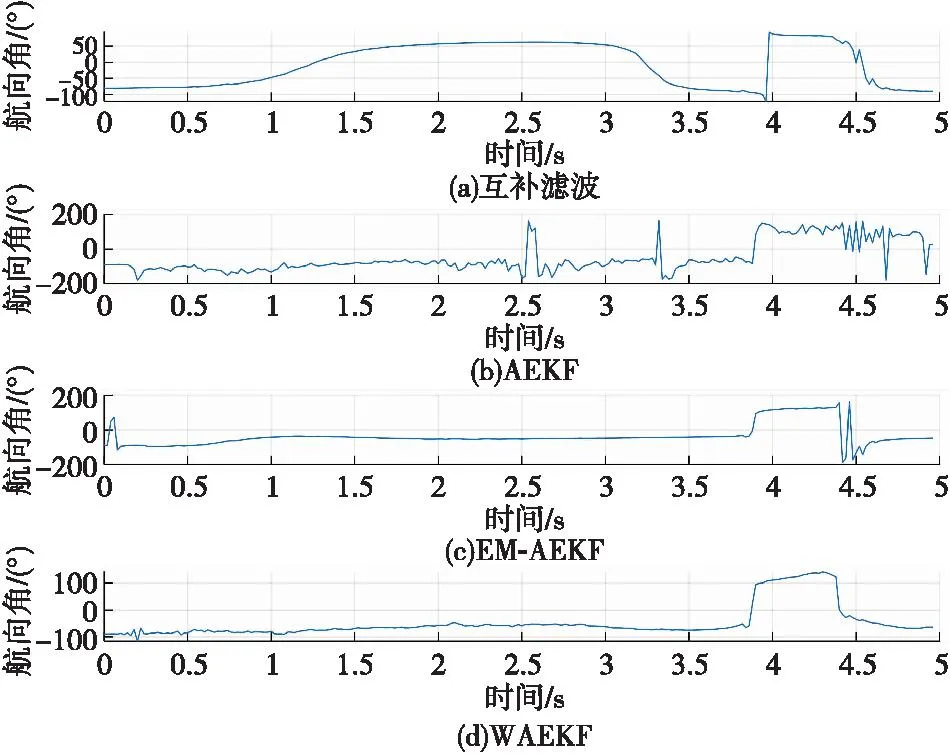
图7 多角度变化运动下航向角对比图Fig.7 Comparison of heading angles under multi angle changing motion

由图7可知,基于互补滤波方法解算的航向角误差最大,发生明显漂移。AEKF解算的航向角存在尖峰值,并且在4.4 s后解算的航向角存在明显漂移误差。基于EM-AEKF方法和本文的WAEKF方法解算的航向角值较为接近真实值,但在0.5～3.85 s之间,基于EM-AEKF方法解算的航向角略小于真实值,且波形存在异常尖峰值。基于WAEKF方法解算在多角度变化运动背景下解算航向角的效果最佳,解算的航向角波形变化平稳且不存在异常尖峰值,同样克服了互补滤波、AEKF及EM-AEKF方法解算的航向角存在异常尖峰和漂移等问题,在多角度变化运动背景下同样适用。

综上所述,可知基于WAEKF方法姿态解算精度整体优于其他三种方法,姿态解算时能够自适应滤除噪声影响,解算角度精度较高,具有优越性和可行性。

4 结论

本文对测量噪声协方差矩阵的估计公式进行了改进,设置权重值对测量噪声协方差矩阵进行调节,提出一种基于优化加权自适应的扩展卡尔曼滤波方法实现姿态解算,解决了滤波发散的问题,提高姿态角度解算的精度。利用本文方法实现惯性传感器测量数据的姿态解算,验证本文方法的有效性,对陀螺仪数据采用基于四元数的龙格-库塔法求得姿态运动模型,建立状态方程,将地磁计和加速度计的数据作为测量信息,利用优化加权的自适应因子调节测量噪声协方差矩阵,控制测量残差的影响,经过不断递归更新能够自适应滤除测量噪声,估算出最优的姿态角。实验表明,相较于传统的自适应扩展卡尔曼滤波算法,本文方法解算姿态的误差得到了较大的改善。