基于多尺度色散熵与支持向量机的调频引信扫频干扰信号识别方法
周 文,郝新红,杨 瑾,蔡 鑫,钱鹏飞
(北京理工大学机电动态控制重点实验室,北京 100081)
0 引言
在现代战场日趋复杂的电磁环境中,各种有源电子干扰设备的出现,对调频引信等无线电引信构成了巨大威胁[1-2]。作为对抗电子干扰手段的第一步,对干扰信号的有效检测识别是进一步采取干扰抑制手段的前提[3]。根据国内外文献资料,现有干扰信号检测识别方法主要分为三个方向:自适应阈值检测,变换域处理检测及信号统计特征检测。
在自适应阈值检测方向,文献[4-5]通过计算当前信号样本的平均功率,设置自适应干扰功率检测门限,当信号功率高于检测门限,则判定信号中包含干扰信号,但此类门限检测方法对低功率干扰检测效果较差且门限设置依赖经验。在变换域处理检测方向。文献[6-7]通过将时域信号转换到时频域中,检测时频域中是否存在异常时频轨迹,从而判定是否包含干扰信号,但其计算较为复杂且所需存储资源量大。在信号统计特征检测方向,文献[8]提出一种基于信号香农熵结合奇异值分解,并利用支持向量机进行干扰信号识别;文献[9]提出一种基于频域香农熵及峰值比并结合贝叶斯分类器的干扰信号检测方法。但香农熵对于噪声较为敏感,在低信噪比环境中特征提取效果不佳。
针对香农熵的局限性,近年来一些新型熵值计算方法,如多尺度样本熵(MSE)[10],多尺度模糊熵(MFE)[11],多尺度排列熵(MPE)[12],多尺度色散熵(MDE)[13]等受到了广泛关注。其中MDE通过非线性映射方法,计算序列在不同时间尺度下的类别丰富程度,提高了对噪声及异常值的鲁棒性,计算效率高,特征表达稳定,在描述时间序列无序性和复杂程度方面表现出巨大潜力。
基于上述分析,本文提出一种基于MDE的调频引信干扰信号检测识别方法,直接在时域进行处理,提取调频引信差频信号的MDE作为信号特征,无需进行变换域操作,并进一步结合SVM分类器,实现了对不同强度下干扰信号的有效检测识别,为进一步采取合适的抗干扰手段提供可靠依据。
1 调频引信差频信号分析
1.1 目标信号特征分析
以锯齿波调频引信为例,根据调频引信工作原理,发射信号xt(t)可表示为
(1)
式(1)中,f0为初始频率,Tm为调制周期,B为调制带宽,β为调频斜率,n为当前时刻对应的周期数,rect[·]为矩形窗函数,则回波信号xr(t)可表示为
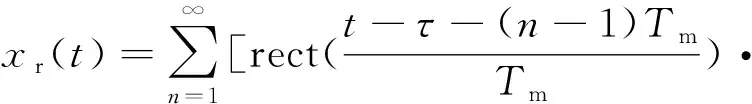
(2)
式(2)中,τ为目标回波经过的路径时延。忽略非规则区影响,经过低通滤波器后,差频信号xΔf(t)可表示为
(3)
目标信号差频频率Δf可近似表示为
Δf=βτ。
(4)
根据式(4)可知,仅目标作用下的差频输出信号在较短的时间窗内可近似为一个单点频信号,如图1所示,其时域波形较为规则,序列复杂度低。
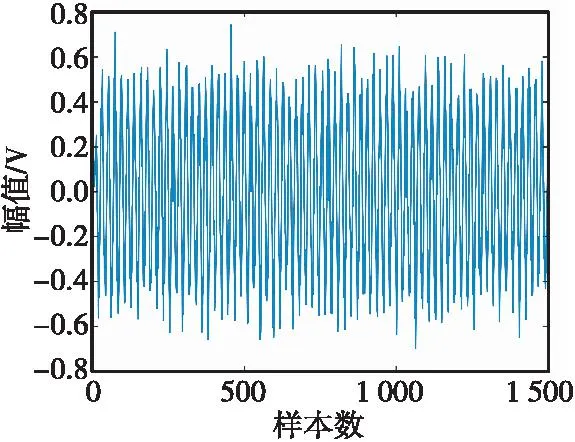
图1 目标作用下的差频信号时域波形Fig.1 Time domain waveform of target beat frequency signal
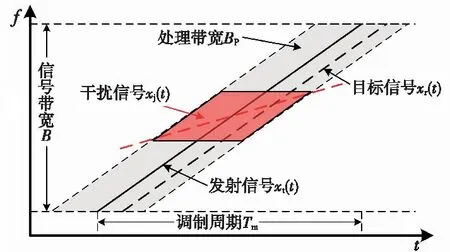
图2 干扰原理示意图Fig.2 Schematic diagram of jamming principle
1.2 干扰信号特征分析
干扰机对引信进行扫频干扰时,扫频带宽会覆盖引信工作带宽,扫频信号的载频会在扫频带宽内按设定规则进行跳变。以单音扫频干扰为例,扫频干扰信号xj(t)可表示为
(5)
式(5)中,fj为当前时刻扫频干扰信号xj(t)主要频率,βj为扫频干扰信号的调频斜率。当扫频信号进入调频引信发射信号的有效频率范围,即可在混频器中产生相应输出。
扫频干扰信号xj(t)与调频引信本地参考信号混频后,所得输出信号xΔfj(t)可表示为
xΔfj(t)=ej(2π(f0-fj)t+π(β-βj)(t-(n-1)Tm)2)。
(6)
进一步可以得到干扰信号差频频率Δfj
Δfj=f0-fj+(β-βj)(t-(n-1)Tm)。
(7)
考虑到引信信号处理带宽BP,差频信号的有效频率范围Δfj还应满足
-BP≤Δfj≤BP。
(8)
由式(7)、式(8)可知,扫频干扰作用下,调频引信差频输出信号xΔfj(t)可近似表示为一个带宽受限的调频信号,其有效调制带宽大小由调频引信信号处理带宽BP决定。由图3可以看出,由于扫频干扰下差频输出信号的频率成分更为丰富,对应的时域波形的复杂度得到了显著提升。
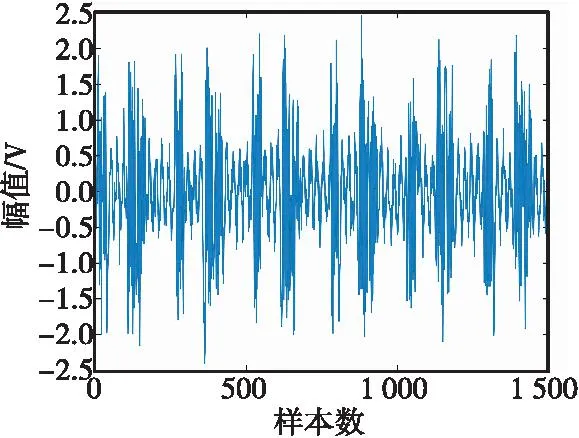
图3 干扰下差频信号时域波形Fig.3 Time domain waveform of jamming beat frequency signal
2 MDE特征提取方法
2.1 色散熵
时间序列的色散熵(DE)计算步骤如下:
1) 首先对于长度为N的原始时间序列X={xi,i=1,2,…,N},通过映射函数转换为新的时间序列Y={yi,i=1,2,…,N}。映射函数可以分为线性映射和非线性映射,考虑到干扰引入的异常峰值的影响,此处选用非线性映射函数中的正态分布函数:
(9)
式(9)中,μ为X的期望,σ为X的标准差,通过式(9),yi可能的取值范围为(0,1)。
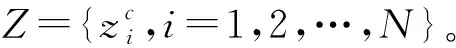
(10)
式(10)中,round(·)为取整函数。
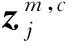
(11)

4) 计算不同散布模式χv0v1…vm-1的出现概率P(χv0v1…vm-1):
(12)


(13)
原始时间序列X的DE值越大,则表明序列中所包含的散布模式越丰富,对应序列的无序性和复杂程度越高。
2.2 多尺度处理
多尺度处理的计算步骤如下:
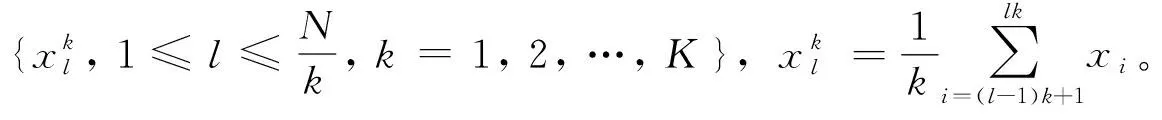
2) 对于每个序列分别计算DE值,进一步得到MDE值:
MDE(X,k,c,m,d)=DE(Xk,c,m,d)。
(14)
多尺度处理过程如图4所示。通过上述多尺度处理,可以得到原始时间序列X的MDE值,进一步表征了其在不同时间尺度上的特征[14-15]。

图4 多尺度处理过程Fig.4 The process of the multiscale method
3 仿真实验及分析
3.1 仿真实验数据获取及分析
为了进一步验证MDE特征对不同干扰水平下差频信号检测识别的有效性,通过仿真手段获取不同干扰水平下的差频输出信号样本,相关仿真参数设置如表1所示。
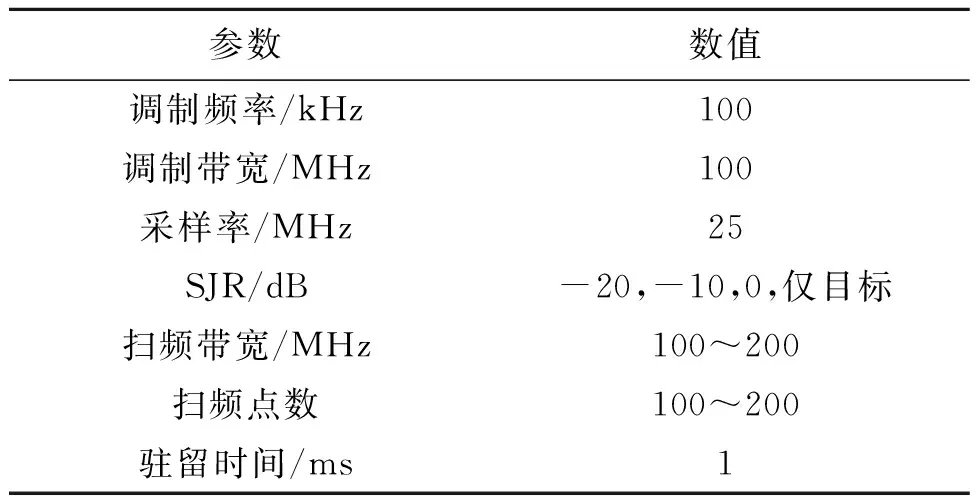
表1 仿真参数设置Tab.1 Simulation parameter settings
通过蒙特卡洛实验,分别获取100组不同条件下差频信号时域波形样本,样本长度设为1 500点,如图5所示。
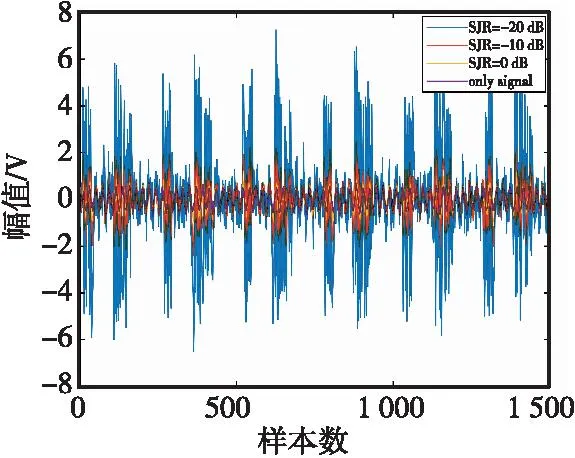
图5 不同SJR下差频信号时域波形Fig.5 Time domain waveform of beat frequency signal under different SJR
由图5可以看出,无干扰条件下仅包含目标的差频信号较为规则,时域波形复杂度低;不同干扰水平下的差频信号随干扰水平的增加,其时域波形复杂度有明显提升。
3.2 不同熵值算法特征提取效果分析
MDE算法的特征提取效果受嵌入维数m与类别c的选取影响较大,合理取值对最终检测效果有较大影响。对于嵌入维数m,若取值过小,将无法检测信号的波动特征,反之若取值过大,将丢失信号细节特征。对于类别c,若取值过小,类别数将不足以分离不同变化特征,反之若取值过大,将对抗噪性能造成一定损失。根据文献[16]的参数设置建议,嵌入维数m取值2~4,类别c一般设为3~8,延迟时间d取值为1,序列长度N一般大于1 000[17]。
为进一步对比MDE和其他熵值算法的特征提取性能,本文另外选取了MSE,MPE,MFE三种方法作为对照,相关参数设置如表2所示。

表2 不同熵值方法的参数设置Tab.2 Parameter settings for different entropy methods
依次计算样本数据的MSE,MPE,MFE,MDE的均值与标准差,如图6所示。
由图6可以看出,当尺度因子较小时,样本数据受噪声影响大,MPE,MSE,MFE及MDE四种算法所得熵值均较高,无法反映样本数据的真实特征;随着尺度因子的增大,对样本数据的平滑程度增大,平滑后的样本数据复杂度降低,不同算法所得熵值的均值明显减少;当尺度因子进一步增大时,对样本数据的过度平滑使得样本间的特征差异变小。因此,选择合适的尺度因子,对准确区分不同条件下的差频信号具有重要影响。
对于MPE算法,由于其只考虑样本数据绝对幅值的排列顺序,没有考虑相对幅值的大小,即熵值会对数据幅值的微小改变而产生较大变化,受噪声影响大。由图6(a)可以看出,MPE算法所提取的特征无法有效区分不同条件下的差频信号。
对于MSE算法,其首先计算样本标准差设置硬阈值门限,并统计数据样本间最大差值过门限的个数,进一步计算其熵值,但基于硬阈值门限的统计方法,无法反映过门限样本间的幅值差异。由图6(b)可以看出,MPE算法所提取的特征能够有效区分仅目标作用下的差频信号与干扰作用下的差频信号,但对不同干扰水平下的差频信号检测效果较差。
对于MFE算法,其在MSE算法的基础上,通过非线性函数的映射,将硬阈值门限替换为软阈值门限,能够细致反映样本间幅值差异分布特征。由图6(c)可以看出,MFE算法所得不同条件下的差频信号熵值的均值差异明显,但标准差偏大,对应的特征鲁棒性有待提升。
对于MDE算法,其结合了MPE和MFE的特点,不仅通过非线性映射细化幅值差异分布特征,而且考虑了映射后新样本序列的排序特征,能够更稳定的提取样本序列的复杂特征。由图6(d)可以看出,MDE算法所提取的特征能够有效区分不同条件下的差频信号,所得熵值的均值差异明显,且熵值具有较小的标准差,特征表达稳定。
3.3 基于SVM的检测识别
SVM作为一种简单高效的广义线性分类器,其基本思想是在结构风险最小化原则的基础上,由核函数将原始数据映射到高维特征空间,通过寻找最优超平面实现对原始数据的分类。结合上一节分析,本文选用尺度因子k取值为3,4,5,6对应的MDE值组成特征向量,结合SVM分类器对不同条件下的差频信号进行检测识别,并通过十折交叉验证获得该方法的检测准确率pr,检测识别结果如表3所示。本文中的检测准确率pr定义如下:

表3 基于仿真数据的差频信号检测结果Tab.3 Results of beat frequency signal detection based on simulation data
(16)
根据表3可知,基于MDE与SVM分类器检测识别方法对仿真所得不同条件下的差频信号均达到了较高的检测准确率,具有较强的检测识别能力。
4 结论
本文提出一种基于MDE与SVM分类器的调频引信干扰信号检测识别方法,通过提取调频引信差频信号在不同时间尺度下的MDE值组成特征向量,结合SVM分类器实现了对不同干扰水平下差频输出信号的有效识别。
1) 分析了扫频干扰对调频引信的干扰原理,指出了当干扰发生时,差频信号复杂度明显提升的特点,提出利用MDE特征来定量描述其特征;
2) 分析了不同熵值算法的特征提取效果,进一步验证了MDE特征的有效性;
3) 通过仿真实验验证了本文方法对不同干扰水平下差频信号检测识别的有效性。
本文方法可用于对当前受干扰程度的定量衡量,无需进行复杂的变换域处理,为进一步决定如何采取合适的干扰抑制手段,如载频捷变、调制参数捷变等提供了可靠依据,有助于确定合适的引信工作频段,实现对干扰频段的规避,保证引信发挥正常的工作效能。

