近远场统一的广义RCS定义及其对雷达方程的拓展推导

马 捷,周世钢,施坤林,黄 峥,米海涛,陈 曦,马岸英,李建瀛,李 铁,李楚宝,李 岗

(1.西安机电信息技术研究所,陕西 西安 710065;2.西北工业大学,陕西 西安 710072;3.北京理工大学,北京 100081)

0 引言

雷达散射截面(radar cross section,RCS)是衡量目标在特定状态下对入射电磁波的散射能力的物理量,在雷达原理中有着至关重要的作用,是用于雷达链路预算、体制参数确定以及探测性能评估等工作的核心参数之一。传统雷达散射截面的定义为[1]

(1)

式(1)中,E0为照射到目标上的入射波的电场强度,Es是雷达所在处的散射波的电场强度。

式(1)要求雷达和目标间的距离是无限大的量,这种限制实际上要求RCS的适用场景具备三个条件:1) 散射目标离发射天线足够远,使得入射电磁波可以看作平面波,即相对于发射天线口径,距离足够大;2) 散射场点位置距离散射目标足够远,散射计算满足远场条件,即相对于目标大小,距离足够大;3) 接收天线距离目标足够远,使得接收天线口径处电场等幅同相,即相对于接收天线口径,距离足够大。

实际在雷达工作时,距离散射目标也不可能都是无限远。对于传统RCS适用的距离,借用天线远区场的概念,文献[2]给出了满足远场条件的距离近似计算公式,雷达的工作频率越高,满足远区场条件的距离越远。近年来在军用、民用雷达领域,尤其是各类近程雷达探测领域(如汽车雷达、室内定位系统、导引头、引信等),探测频率越来越高,毫米波、太赫兹频段应用越来越广泛,对目标RCS达到平方米量级的物体探测的远场条件往往需要达到几公里甚至十几公里,传统RCS定义需求的远场条件不再满足,因此需要对RCS的计算做进一步修正,完善传统RCS基本定义即公式(1),将R趋于无限大的条件消除掉,形成能够统一近远场的广义RCS定义。

从20世纪80年代起,国内外学者便对近场RCS展开研究。早期,部分学者将几何尺寸较大的散射目标的近场散射问题划分为由许多小尺寸单元组成的目标散射问题[3],对于每一个单元而言,均能满足雷达探测的远场条件,因此目标的总RCS则定义为各个单元RCS的叠加。然而,这种方法没有考虑各个单元间的内在耦合,导致计算结果不准确。文献[4]基于远场RCS引入了天线远场辐射方向图和增益来定义近场RCS,很多研究人员基于此定义进行了近场RCS的计算以及系统分析[5-9]。文献[10-11]分析了天线远场辐射方向图对于近场RCS特性的影响。可以看出,上述文献定义的RCS和外加天线远场辐射方向图特性有关。而RCS是反映目标对于电磁波散射能力的物理量,只能与目标本身有关,不应该与发射(或接收)天线的特性相关。

文献[12]直接采用式(1)的形式对目标的RCS进行定义,R选取为实际天线到目标几何中心的距离,天线采用全向辐射天线。该定义不再考虑天线对于散射目标RCS影响,但是该定义难以反映目标局部照射时的情况,在具体进行雷达系统分析计算中应用该定义会产生较大误差。文献[13]采用在散射目标表面加单位包围面,引入电偶极子和磁偶极子,对近场RCS进行了重新定义,然而基于此定义计算雷达收发信号关系时需要输入目标物理尺寸信息,不能实现系统评估过程的数据化计算,分析雷达收/发信号时仍然采用天线远场辐射方向图,没有摆脱天线的远场条件限制。

参考传统RCS定义在雷达领域应用的普适性和简便性,近场散射RCS的定义需要具备以下三个特征:

1) 近场散射RCS仅与目标形状、材质以及与收发天线的相对位置有关,与收发天线的辐射参数无关;

2) 广义RCS定义能够统一近远场电磁散射特性,当探测距离由近及远逐步趋于远场条件时,其定义应自然简化为传统RCS定义;

3) 涉及雷达系统计算时,RCS数据可以代替目标本身,完全实现目标数据化,有利于进行数据化计算。

本文基于电磁场等效原理,在目标周围构建封闭包围面,给出了新的广义RCS定义。在新的广义RCS定义的基础上进而对Friss公式进行了近场拓展。通过利用天线近场口径特征辐射数据代替传统远场辐射方向图数据,结合散射目标广义RCS数据和相对位置关系数据,给出了计算雷达接收功率的方法,计算结果和利用FEKO软件的全波仿真相比,近场和远场的计算结果均吻合良好,表明本文广义RCS定义以及Friss公式拓展方法的正确性和有效性。值得强调的是,基于本文提出的广义RCS定义,可以为涉及近场探测的各类军用、民用近程雷达(包括汽车雷达、室内定位系统、引信、导引头等)的系统设计、参数选择、近场目标探测识别与抗干扰特性估计,以及近场条件下的标准RCS测试方法构建,雷达目标强散射点分析,目标微波成像算法设计等提供理论基础与计算依据,为近程雷达理论体系的构建提供理论支撑。

1 广义RCS定义

1.1 等效原理算法

等效原理(惠更斯原理)是指一个封闭曲面内或者面外的电磁场可以用包围这个面上的等效切向电磁流来描述出来。电场和磁场可以用以下公式表示[14]:

(2)

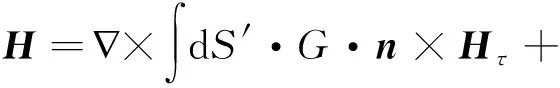
(3)

式中,Eτ和Hτ是指包围面上的电场和磁场,n为包围面的法向单位矢量,G为格林函数,n×Eτ和n×Hτ相当于包围面上的等效电流和等效磁流。从上述公式可以看出,已知封闭面上的电场(磁流)和磁场(电流)信息就可以计算封闭面内或者封闭面外任意一点的辐射电场和磁场。等效原理算法为包围面上数据代替散射目标本身提供了基础的理论支撑,也是本文广义RCS定义的理论基础。

1.2 广义RCS定义及推导

基于等效原理算法,我们在目标(散射体)周围构建包围面,如图1所示。由等效原理可知,包围面到目标的距离可以任意给定,对包围面进行离散化,用包围面上各个部分的电场和磁场数据代替目标,实现目标数据化的目的。

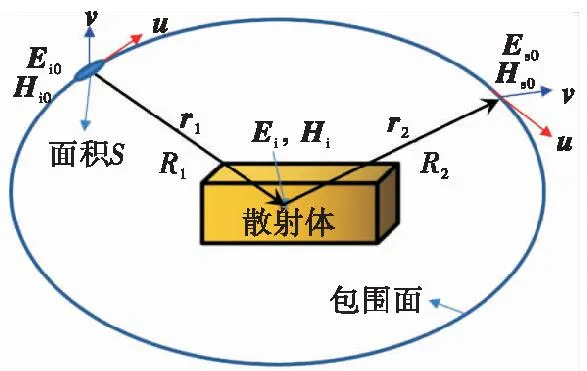
图1 散射体和包围面结构示意图Fig.1 Configuration of scatter and enveloping surface

具体定义如下:

Ei0,Hi0为包围面上入射切向电场和磁场;

Es0,Hs0为包围面上散射切向电场和磁场;

Ei,Hi为散射体几何中心处电场和磁场;

u,v为包围面切向正交矢量;

R1,R2为包围面到散射体几何中心距离;

S为包围面上离散小面元面积;

r1,r2为入射点和散射点到几何中心矢量。

借鉴传统RCS定义(即式(1))方式,广义RCS定义如下:

(4)

式(4)中,Es0为包围面上某点的散射电场,Ei为包围面上某点入射电场Ei0在散射体中心点处产生的电场。由式(2)可知:

(5)

将式(5)代入式(4)可将RCS定义中包围面上的散射场和目标处电场的关系转化为包围面上散射场和入射场的关系,进一步化简可得:

(6)

式(6)中,u,v为包围面上入射电场的单位方向矢量。进一步将式(6)写成更一般的公式,可得广义RCS定义的一般表达式:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

由于包围面的离散化,式(8)-式(23)给出的广义RCS定义可以写成矩阵形式,矩阵维度的大小和包围面的离散数相关。包围面上入射场和散射场之间的关系可以通过测试和仿真的方法获得。由等效原理可知,包围面上的数据具有完备性,任一包围面上的数据可以推导其他任何位置的场数据。通过本文计算公式(7)也可计算任意距离和方向的RCS值,当距离足够大时,可实现远近场RCS计算结果的统一。

1.3 基于广义RCS定义的计算与仿真

为了验证式(7)的有效性,对典型目标(平板、圆柱和圆球)进行了计算和仿真,仿真采用FEKO矩量法,方形平板边长为0.5 m,圆柱直径和长度均为1 m,球的直径为0.6 m,工作频率设为1 GHz,入射场和散射场都处于目标的正上方,仿真和计算的RCS结果随距离R1(雷达和目标中心点距离)变化情况如图2所示。

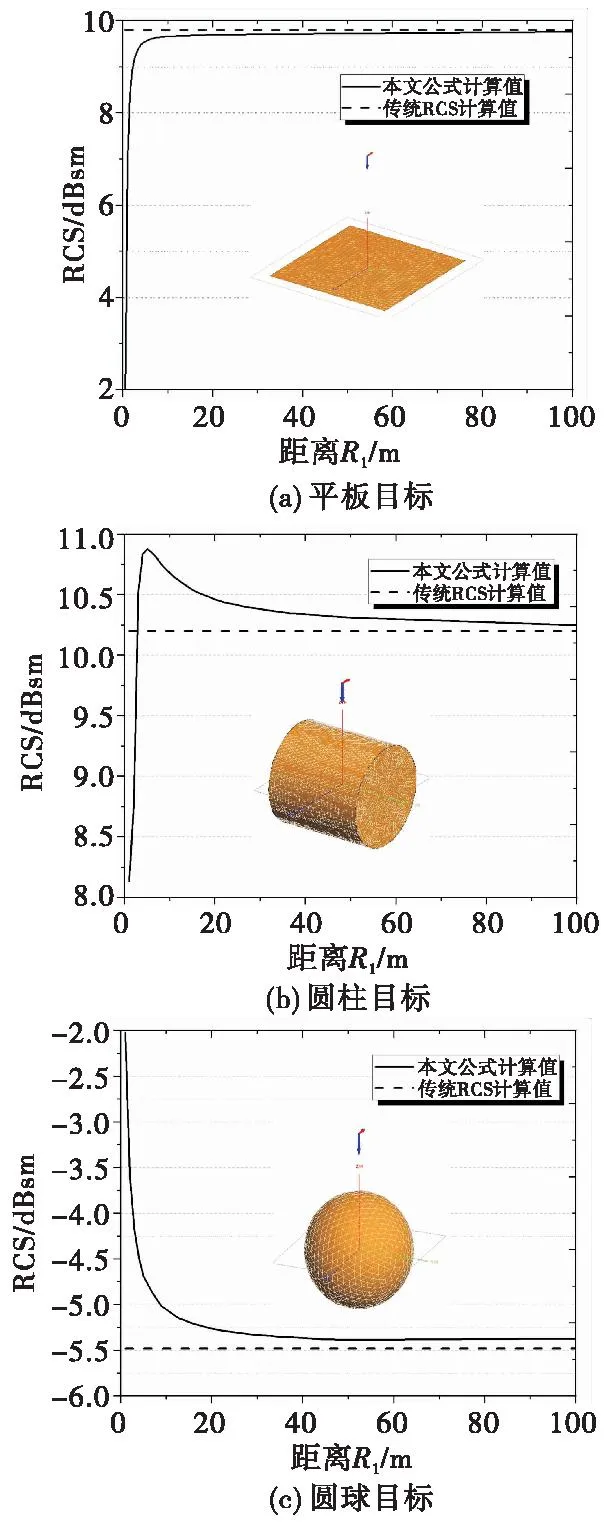
图2 典型目标RCS仿真和计算结果Fig.2 Simulated and calculated RCS results of typical object

从图2结果可以看出:当距离足够大时,本文定义计算结果和传统RCS计算结果吻合良好;距离较近时,对于平板,不能看做平面波所以场不能进行同向叠加,所以RCS值会变小;球体目标上各点在远场由于存在波程差散射场存在部分抵消,所以在近区RCS反而更大;圆柱目标随着距离由远及近RCS值先增大后减小。上述计算结果与实际物理情况也是符合的。

2 基于广义RCS定义的雷达方程拓展

雷达系统设计的源点是雷达基本方程,而RCS是雷达方程中的核心参数之一。Friss公式是雷达基本方程的核心组成部分,用来计算雷达接收功率,公式如下:

(24)

从式(24)可以看出雷达接收功率和发射功率、收发天线的特性(远场辐射方向图增益)、目标特性(RCS值)、工作频率以及收发天线与目标的相对位置关系(R1,R2)有关。因此近场条件下的雷达收发功率也应该与上述类似因素相关。

式(24)中的天线远场辐射方向图和目标RCS都是需要雷达和目标之间的距离足够远,近场条件下都需要用新的参数进行替代,目标RCS可以用本文公式(7)中的广义RCS定义进行替代。由等效原理可知,天线包围面上的辐射电场(磁流)和磁场(电流)数据可以对天线进行替代,包围面离天线足够远,辐射数据即为远场辐射方向图数据。由于天线辐射有一定的方向性(对于高增益天线尤其如此),因此我们将包围面上包含辐射场的口径上的数据对天线进行替代。包含辐射场的口径看作天线的近场辐射口径,天线的近场口径特征辐射数据定义为天线在单位电压激励下的特定近场口径上的电场和磁场辐射数据。天线近场口径特征辐射数据只与天线的辐射特性有关,与馈电的多少无关,因此定义为特征辐射数据,在近场条件下可对式(24)中的远场辐射方向图进行替代。如图3所示,天线的近场口径特征辐射数据根据天线的辐射特性选取口径,离散化的选取口径面上的电场和磁场特征辐射数据,这些数据可以通过天线仿真或测试获得。

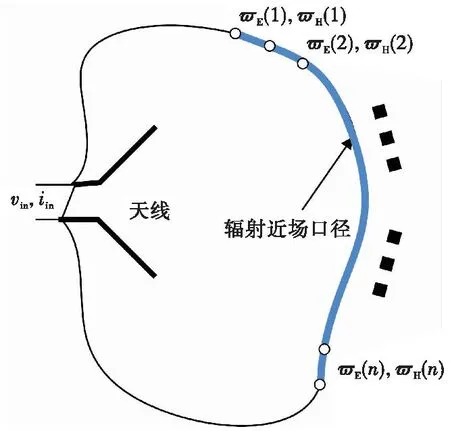
图3 天线近场口径特征辐射数据Fig.3 Near-field aperture characterized radiation data of an antenna

2.1 一些新的定义和运算规则

为了运算和表示简单,首先可以将式(2)和式(3)写成矩阵的形式,为此我们先定义新的运算符号和规则为

C=A⊗B,

(25)

式中,B和C为矢量列向量,A为矢量矩阵,如下:

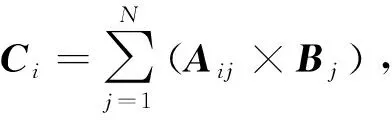
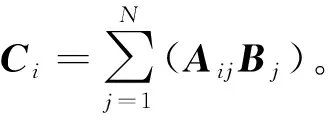
上述三种运算连乘时,从右到左进行运算,例如:D⊗C=D⊗(A⊗B)=D⊗A⊗B,其中D为矢量矩阵。

2.2 近场条件下接收功率计算方法

图4给出了收发天线和目标的相对位置及各参数的示意图,类似于式(24),已知发射功率、收发天线的近场口径特征辐射数据、目标广义RCS矩阵以及收发天线和目标的相对位置关系,就可以求得接收功率。

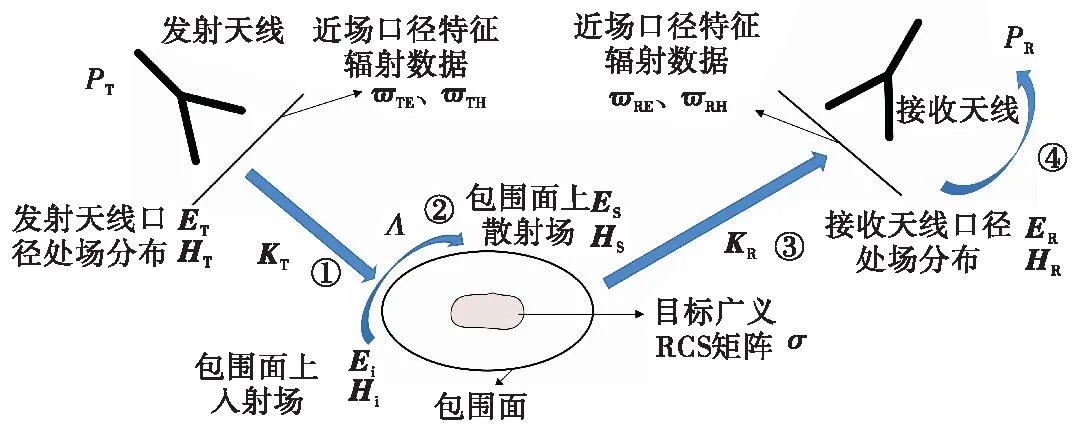
图4 收发天线和目标相对位置及参数示意图Fig.4 Configuration and parameters of transmit and receive antennas and object

因此已知的参数包括:

1) 发射天线近场口径特征辐射数据,包括:近场口径场采样数nT;采样点周围面积ST(nT),面元单位法矢量nT(nT);发射天线近场口径特征辐射数据ϖTE(nT),ϖTH(nT)。

2) 接收天线近场口径特征辐射数据,包括:近场口径场采样数nT;采样点周围面积SR(nR),面元单位法矢量nR(nR);接收天线近场口径特征辐射数据ϖRE(nR),ϖRH(nR)。

3) 散射体目标的广义RCS矩阵数据,包括:等效面采样点与中心点距离r1,r2;等效面上的采样数nσ;等效面每个采样点对应面积Sσ(nσ);16个广义RCS矩阵σeueu,σeuev,…,σhvhv。

4) 相对位置参数数据,包括:发射天线与散射体的相对位置(uT,vT,nT),接收天线与散射体的相对位置(uR,vR,nR)(u,v,n为三维坐标值)。

求接收功率的过程可以分为四个步骤:

1) 求目标包围面上任意一点的入射场Fi。

在已知发射天线近场口径特征辐射数据和发射功率条件下,如图4所示,可以计算发射天线口径处的实际辐射电场和磁场ET和HT。利用式(2)和式(3)可以求得散射体包围面上任意一点的入射电场和磁场数据。借助式(25)的运算规则,公式如下:

(26)

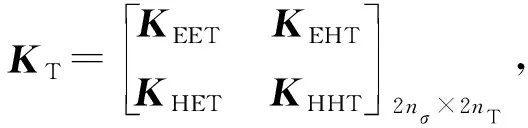
KEET(i,j)=ST(j)∇×G(i,j)nT(j),

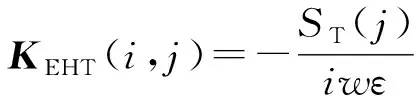
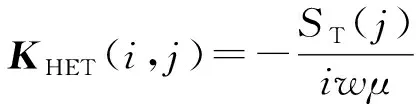
KHHT(i,j)=ST(j)∇×G(i,j)nT(j)。

上式中G(i,j)为发射口径场点到包围面入射场点的格林函数,通过KT矩阵运算可以由发射天线近场口径处辐射场数据获得包围面上入射场数据。

2) 计算目标包围面上的散射场强度Fs。

由于式(8)-式(23)中的广义RCS定义反映了包围面上散射场和入射场之间的关系,因此可直接用广义RCS矩阵进行包围面上散射场的计算。借助于2.1节中定义的运算规则,可得包围面上的散射场数据,如下:

Fs=ΛFi,

(27)

即

其中:

(28)

(29)

(30)

(31)

(32)

(33)

式(28)中Λ有16种元素,分别对应式(8)-式(23)中的16种RCS,为了书写方便,用式(29)-式(32)表示,其中p,q分别可取u或v。由于散射场和入射场之间关系还需要相位信息,因此式(29)-式(32)中φepeq(i,j),φephq(i,j),φhpeq(i,j),φhphq(i,j)为散射场相位和入射场相位的差。通过Λ矩阵运算可以由包围面上入射场数据获得包围面上散射场数据。

3) 计算接收天线口径处散射场。

由包围面上散射场计算接收天线近场口径处散射场,计算过程和第一步类似,公式如下:

(34)

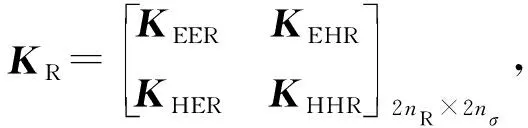
KEER(i,j)=Sσ(j)∇×G(i,j)nσ(j),

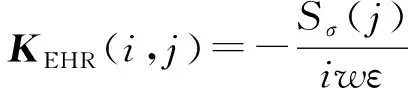
KHHR(i,j)=Sσ(j)∇×G(i,j)nσ(j)。

上式中G(i,j)为包围面散射场点到接收天线口径处场点的格林函数,通过KR矩阵运算可以由包围面上散射场数据获得接收天线近场口径处散射场数据。

4) 计算接收天线的接收功率。

如图5所示,接收天线处于一个场环境中(近场口径上电场和磁场分布为ER和HR),当天线单位馈电(即vin=1 V)时,可以获得接收天线近场口径特征辐射数据(ϖRE和ϖRH)。

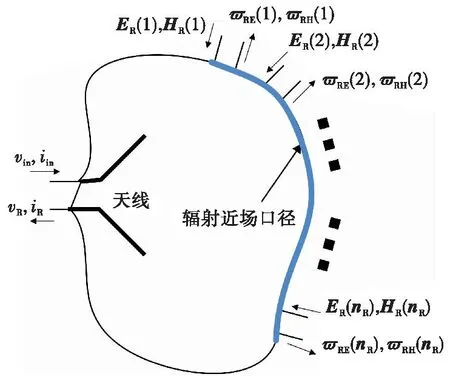
图5 接收天线端口和辐射口径场关系图Fig.5 Relationship between the ports and radiation field of receive antenna

将辐射近场口径离散化,根据互易定理和文献[15]中端口电压和场关系公式可得:

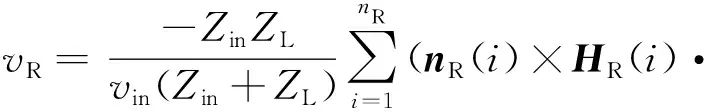
(35)

式(35)中,Zin为天线的输入阻抗,ZL为天线接收时的负载阻抗(一般为50 Ω),当天线完全匹配时,Zin=ZL,可以获得接收功率为

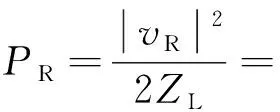
(36)

利用2.1节中定义的运算规则,上式可以写为

(37)

进一步简写为

(38)

因此综合式(26),(27),(34)和(37),我们在近场条件下可以将传统Friss公式(24)扩展到以下形式:

(39)

2.3 算例验证

为了验证上述计算过程,即式(39)的有效性,对典型目标(圆盘、圆柱和圆球)和收发天线(采用矩形波导口天线)进行仿真和计算,仿真采用FEKO矩量法,圆盘半径为1 m,圆柱直径为1 m、长度为2 m,球的直径为1 m,工作频率设为1 GHz,收发天线都处于目标的正上方。在不同距离R1(收发天线到目标中心点距离)处,分别比较了实际全波仿真收发功率比值、利用Friss公式(24)计算比值和本文方法计算比值,仿真和计算结果如图6所示。

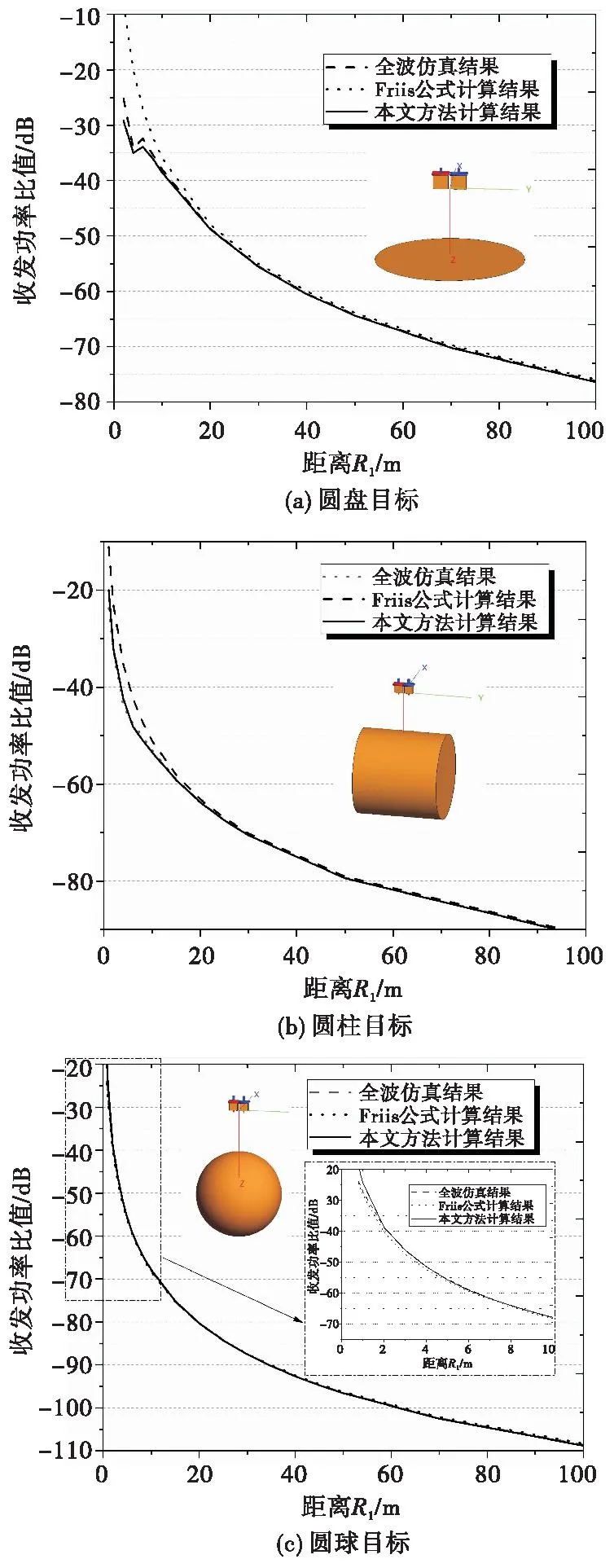
图6 针对典型目标照射的收发功率比值仿真和计算结果Fig.6 Simulated and calculated results of transmit-receive power ratio for illuminating typical objects

从图6结果可以看出当:距离R1足够大时,本文计算结果和Friss公式计算结果都与全波仿真计算结果吻合良好;距离较近时,本文方法明显更接近实际的全波仿真结果;当距离更近时,由于散射体对于收发天线本身的特征辐射场存在影响,因此计算结果和实际全波仿真存在一定的误差,这个问题可以通过目标散射场数据对天线的近场口径辐射数据进行修正,多次迭代降低计算误差。

2.4 可能的应用场景

由于本文广义RCS定义中的数据信息相对于传统RCS定义更为完备,因此在雷达系统中可以具有更加广泛的应用。如图7所示,本文定义的广义RCS可以作为根部技术,支撑雷达领域多个应用场景,可能应用的场景包括但不限于:

图7 广义RCS定义可能应用场景Fig.7 Potential application scenarios for general RCS definition

1) 雷达系统动态数据仿真:本文RCS定义可以在近场条件下实现收发天线和目标的数据化,并实现了解耦,因此在动态弹目交汇等场景的系统仿真可以实现数据化仿真。

2) 近场RCS测试技术:可以根据本文方法测试包围面上的收发场数据,由于数据的完备性,可以推导任意空间任意入射和散射场的比值关系,实现了任意不同位置间RCS值,此方法可以统一远场条件。

3) 目标强散射点分析:由包围面上的数据向目标表面进行场变换,可以对目标进行细颗粒度散射特性分析,寻找目标强散射点(区域)。

4) 目标雷达成像算法:由于可以分析目标本身细颗粒度散射特性,根据高分辨率散射特性和收发天线数据可以构建新的雷达成像算法。

5) 雷达抗干扰算法:由于可以获得更多、更高分辨率目标信息,因此可以分辨出雷达干扰机和目标本身,基于更完备的数据可以开发近场条件下的雷达抗干扰算法。

3 结论

本文基于电磁场等效原理,在目标周围构建封闭包围面,推导出一种广义RCS定义的新方法,这种定义可以对目标远近场的RCS进行统一,可以实现收发天线和目标特性的解耦,并且实现RCS数据对于目标本身的替代。基于本定义,对近场条件下的雷达基本方程进行了拓展,给出了近场条件下雷达接收功率的计算方法,对典型目标进行了仿真计算,结果表明了此方法的有效性。此定义方法可以为远近场条件下的雷达数据仿真、目标特性分析以及成像算法等研究提供理论支撑和工具。