移动荷载作用下悬浮隧道管体TMD减振分析及优化布置

杨 赢, 金利成, 项贻强, 何余良

(1. 绍兴文理学院 土木工程学院, 浙江 绍兴 312000; 2. 浙江大学 建筑工程学院, 杭州 310058)

悬浮隧道(submerged floating tunnel,SFT),是一种跨越宽阔水域的新型交通结构物,其依靠浮力、自质量及锚固系统的作用实现平衡,故又称“阿基米德桥”。根据锚固方式的不同,通常可分为浮筒式、固定支承式和锚索式。悬浮隧道为复杂环境水域的跨越提供了新的可能性[1-2]。目前,锚索式悬浮隧道的研究最为广泛,是最有可能实现的形式。

悬浮隧道在运营期间,除长期受到波流等外部环境荷载外,管体内部移动车辆荷载的作用也不容忽视。基于此,国内外学者对移动荷载作用下悬浮隧道的动力响应问题展开了相关研究,Tariverdilo等[3]将移动荷载简化为常荷载,并考虑了流体附加质量的惯性效应,研究表明增加锚索刚度可以控制移动荷载作用下悬浮隧道的动力响应。董满生等[4]将移动车辆荷载简化为一系列等间距的移动集中荷载,分析了悬浮隧道的位移时程响应。项贻强等[5]基于弹性地基梁模型,将移动车辆荷载等效为移动常荷载,分析了流体作用效应下悬浮隧道的动力响应。Lin等[6]提出一种悬浮隧道在车-隧-流相互作用下动力响应的理论分析模型,讨论了水流流速、浮重比、锚索倾角等多个关键参数的影响。Jin等[7]求解了SFT-锚索-列车耦合动力方程,研究了波浪和地震激励下它们的动力和水弹性相互作用。Xiang等[8]研究了移动车辆荷载作用下悬浮隧道的动力特性,通过模型试验讨论了不同车辆参数和锚索参数对SFT的影响。

近年来,移动车辆荷载作用下结构的动力响应问题逐渐被人们重视。当既有线路上一些桥梁的自振频率与车辆荷载的激振频率接近时,会引发共振现象,导致车辆通过桥梁时的动力响应急剧增大,造成极大的安全隐患,这一现象在悬浮隧道上也不例外。然而,当前对于移动荷载作用下悬浮隧道的振动控制却鲜有报道。

为减小移动荷载作用下悬浮隧道管体的动力响应,本文采用TMD作为减振措施并分析了其减振效果。将悬浮隧道管体简化为弹性地基梁,采用移动简谐力模型,考虑流体的附加惯性效应和阻尼效应,建立了移动荷载作用下悬浮隧道管体和TMD系统振动控制方程组。采用Newmark-β法进行数值求解,分析了TMD对悬浮隧道管体位移的减振效果,讨论了移动速度和TMD阻尼比对减振效果的影响,从而得出TMD的最优参数及适用条件,为悬浮隧道的振动控制提供参考。

1 理论分析模型

图1为典型锚索式悬浮隧道结构示意图。在以管段为研究对象时,可将悬浮隧道锚索视为弹性支撑[9]。Sato等[10]认为在锚索和管体的刚度满足式(1)时,等间距的弹性支撑可进一步简化为连续的弹性地基。

(1)

式中：K为一对锚索的锚固刚度;H为锚索的间距;EI为管体抗弯刚度。

图1 悬浮隧道模型示意图

因此,本文将悬浮隧道管体视为弹性地基梁。TMD安装在管体跨中位置。TMD的构造参考了桥梁减振中广泛应用的经典TMD[11-12],其布置方式如图2所示。

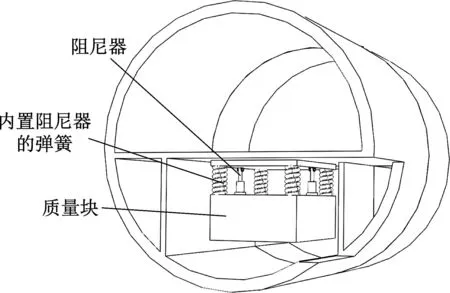
图2 悬浮隧道TMD布置简图

根据汽车荷载作用特点,采用移动的简谐集中力进行模拟[13]。悬浮隧道-TMD系统简化模型如图3所示。

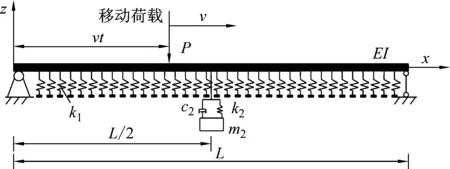
图3 悬浮隧道-TMD系统简化模型示意图

TMD简化为质量块,阻尼器以及弹簧三部分进行模拟[14-15]。基于Hamilton原理,推导建立移动荷载作用下悬浮隧道-TMD系统的竖向振动控制方程,如式(2)和(3)所示

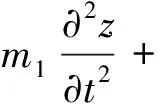
(2)

(3)

根据Morison方程,管体竖向振动引起的流体作用力fD可表示为

(4)

式中：ρ为流体密度;D为隧道管体直径;CD为阻力系数,取CD=0.7;Cm为附加质量系数,取Cm=1.0[17]。

将式(3)和式(4)导入式(2),可得式(5)

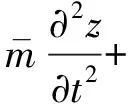
(5)

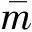
采用振型叠加法对控制方程进行求解,令：

(6)

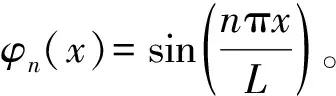
将式(6)代入式(5),并利用振型正交性在等式两边同乘φi(x),在(0,L)上积分可得第i阶广义振型坐标的方程,见式(7)

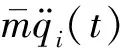
(7)

其中,Di为非线性流体相关项,可表示为

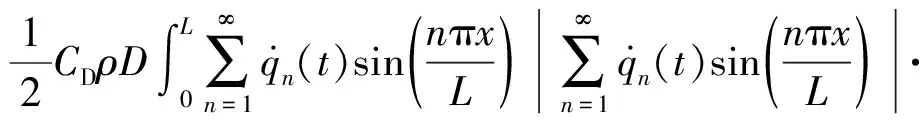
(8)

进一步整理得

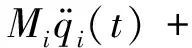
(9)

式中,ωi,Mi,Pi(t),ξi分别为第i阶频率、振型质量、振型广义荷载、振型阻尼比,其表达式为

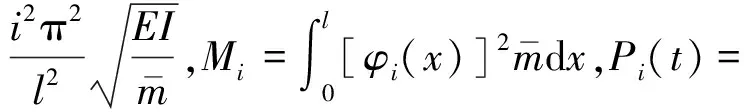
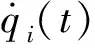
2 数值算例

由于目前世界上仍无悬浮隧道建成实例,本文算例的基本参数参考了已有的研究[19],如表1所示。

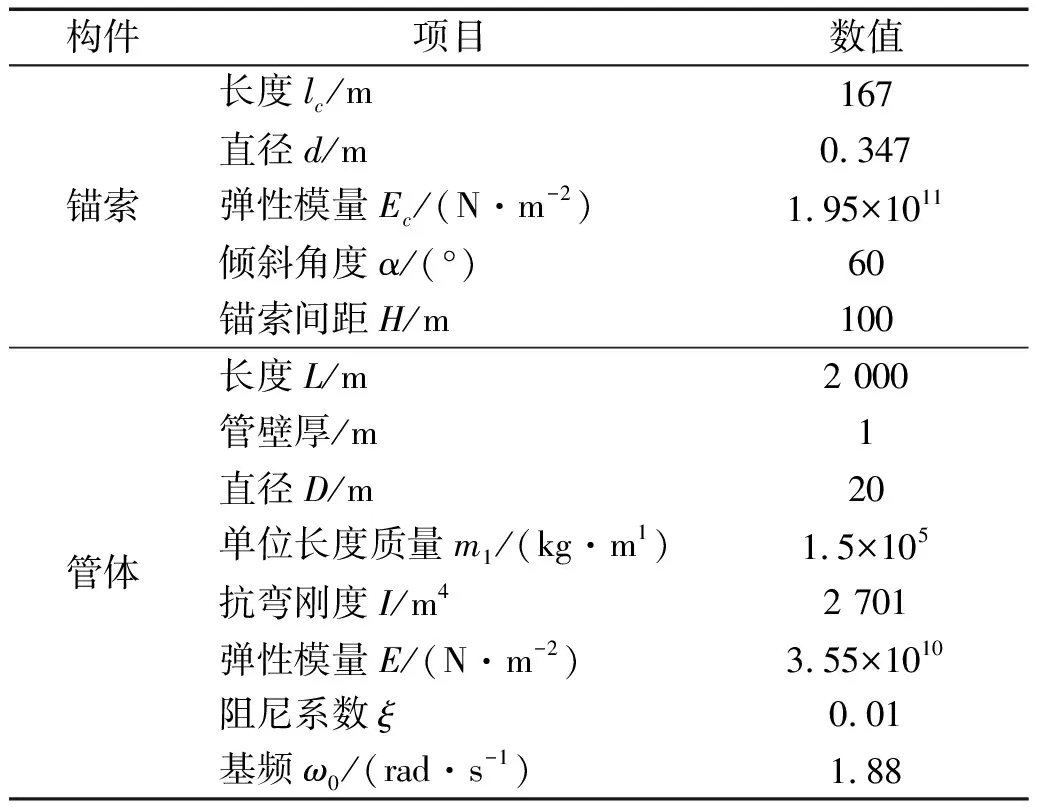
表1 悬浮隧道基本参数

移动荷载值P0和移动速度v的取值参考我国JTG D60—2015《公路桥涵设计通用规范》[20],考虑到双车道,移动简谐荷载值P0取1 100 kN,荷载移动速度v分别为60 km/h,80 km/h,100 km/h,120 km/h。为考虑最不利工况,移动简谐荷载的频率ωp与悬浮隧道基频ω0一致,取1.88。

TMD的主要参数包括质量块质量、阻尼和刚度。通常TMD质量的经济范围可取一阶模态质量的1%～2%[21]。

当忽略主结构阻尼时,TMD最优频率比fopt和最优阻尼比ξopt,可采用式(10)计算[22]

(10)

根据最优频率比和最优阻尼比,TMD的阻尼系数c2和弹簧刚度k2可采用式(11)计算

c2=2ξoptfoptω0m2

(11)

式中：μ为TMD质量和管体模态质量之比;ω0为管体基频;m2为TMD等效质量。

考虑到TMD水下振动受到的流体作用影响,m2可按下式计算

m2=mT+CmρVT

(12)

式中：mT为TMD实际质量;VT为TMD的体积。

结合悬浮隧道参数,本文TMD的参数取值如表2所示。

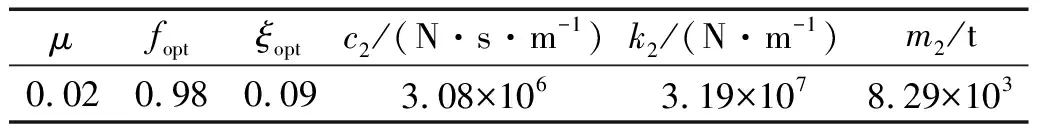
表2 TMD关键参数取值

3 结果分析

3.1 减振效果

图4为简谐荷载移动速度v=80 km/h时,安装TMD前后管体不同位置的竖向位移时程曲线。

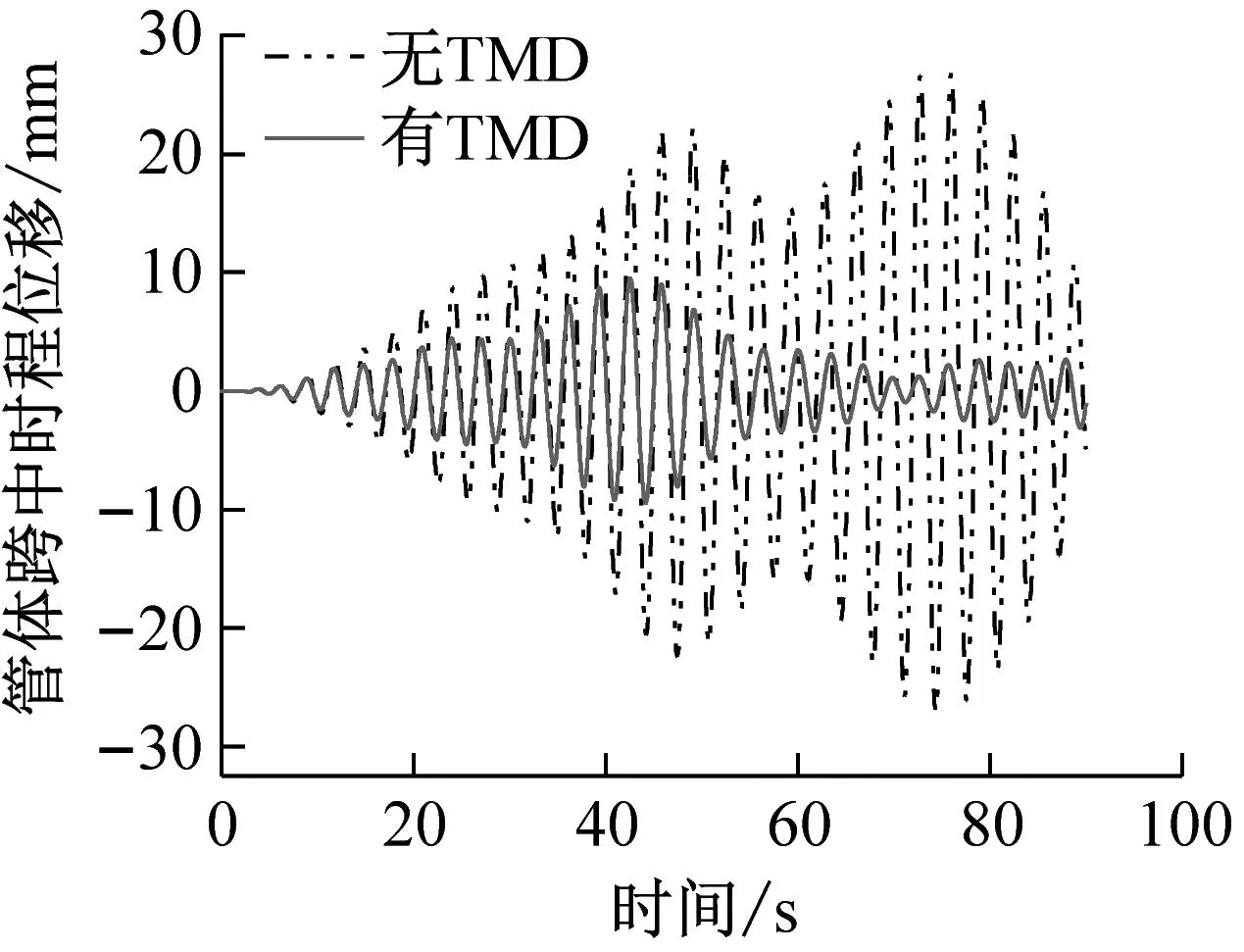
(a) 跨中减振前后位移时程曲线

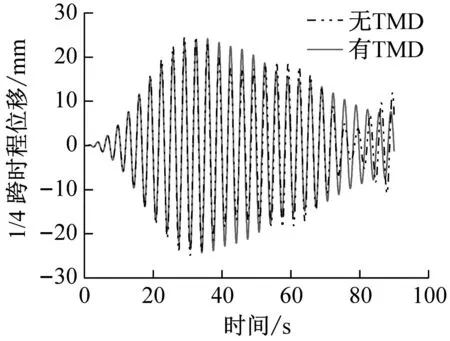
(b) 1/4跨减振前后位移时程曲线

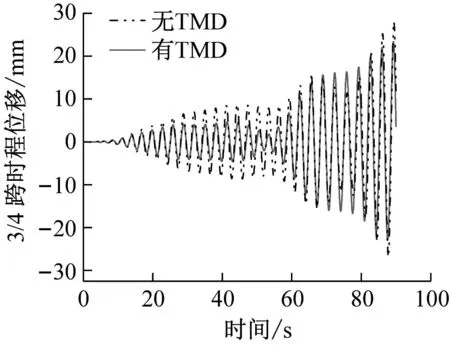
(c) 3/4跨减振前后位移时程曲线

由于简谐荷载频率与管体1阶固有频率一致,管体跨中位移响应逐渐放大,最大位移为26.81 mm;安装TMD后,管体跨中最大位移出现在荷载经过的时刻(t=42.5 s)为9.54 mm,减幅为64.42%,且在移动荷载经过后,管体跨中能保持较小的振幅振动,减振效果显著。而对于L/4处,在荷载未到达跨中位置前,由于TMD振动较弱,对管体没有起到较为显著的减振作用,在荷载经过TMD时反而增大了该处的振动。安装TMD前后3L/4处管体的最大位移分别为25.33 mm和18.07 mm,减振率为28.66%。因此,对于管体的不同位置,TMD的减振效果差异明显。这是由于在移动荷载作用下,悬浮隧道管体的高阶模态被激发参与振动,单一TMD无法同时对各阶模态起到减振作用所致。

表3进一步给出了不同位置达到位移峰值时,前5阶振型的位移贡献量。由表3可知,安装在跨中位置的TMD,对奇数阶的模态具有减振效果,而对偶数阶的振型没有影响。管体跨中振动响应仅由奇数阶模态叠加,因此减振效果最为明显。而对于其他位置,TMD装置并不能保证同时对各阶参振模态起到减振作用,甚至还可能增大某阶模态的振动效果,导致叠加后减振效果降低。

表3 最大位移时刻管体前五阶模态贡献量

为确定单个TMD的有效减振范围,图5给出了悬浮隧道管体沿长度方向的位移减振效果。

由图5可知,TMD只对其安装位置附近一定范围内的管体位移具有明显的减振效果。在此范围之外,其减振作用很小,个别位置甚至出现位移略微增大的情况。对于移动荷载作用下,减振范围向荷载下行方向偏移,这是由于当荷载通过TMD安装位置时,才会激起质量块的大幅共振,增强了其后管体的减振效果。因此,对于有多阶模态参与振动的悬浮隧道管体来说,可考虑设置多个TMD以适应不同模态的减振需求。

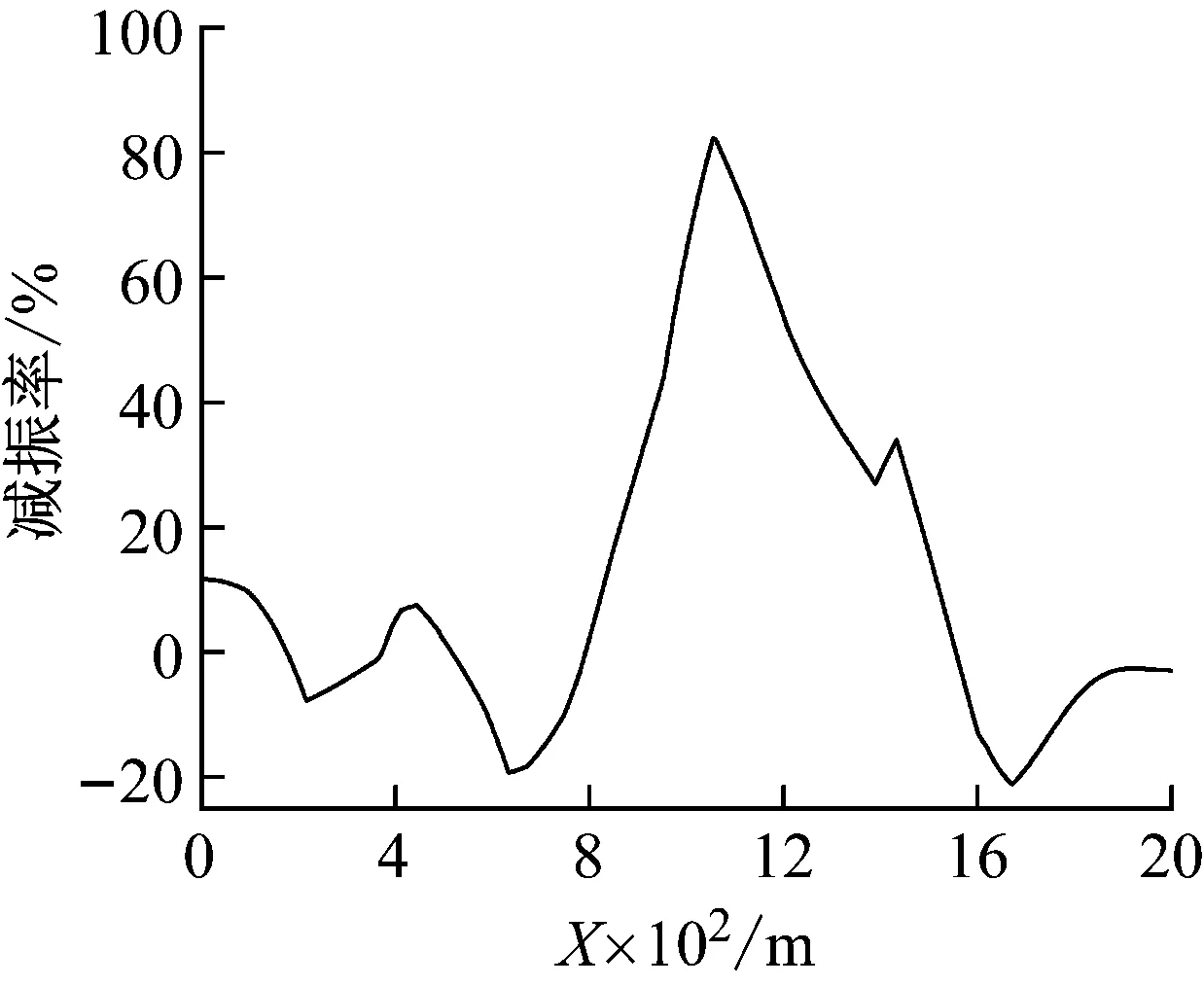
图5 悬浮隧道沿长度方向减振率

3.2 TMD的优化布置

由于跨中单个TMD的减振范围有限,不能达到预期的减振效果,且单个TMD的质量和体积较大,不利于安装,故保持总质量比2%不变的情况下,提出分布式TMD的布置方案,分别位于管体的1/4跨,1/2跨和3/4跨处,如图6所示。

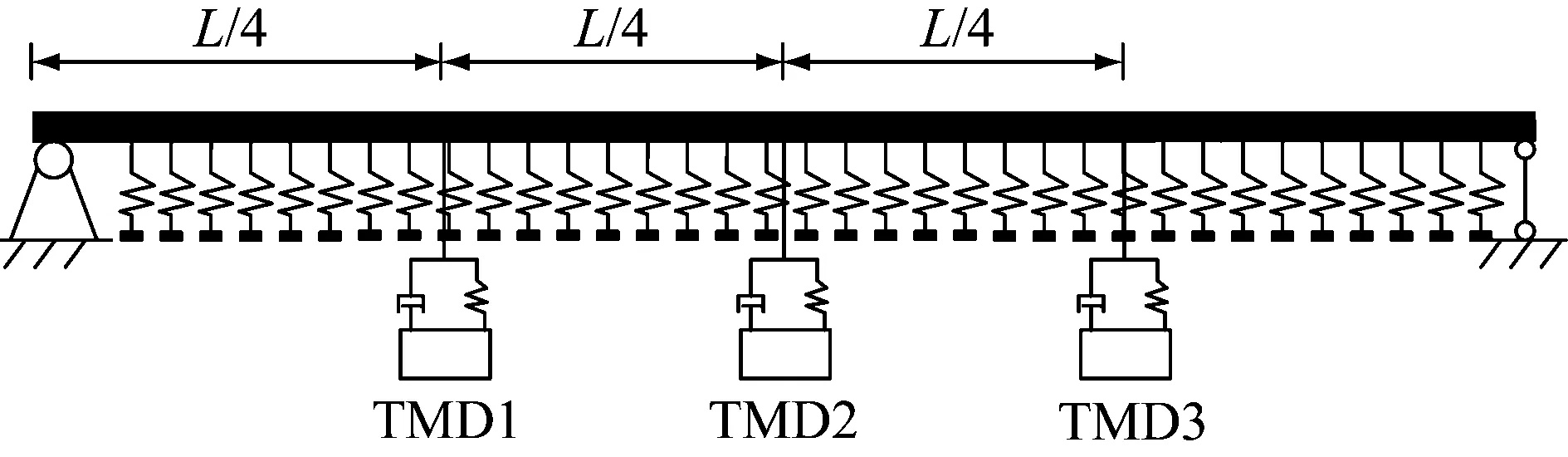
图6 TMD安装示意图

表4给出了四种不同工况下分布式TMD的参数取值。分别对四种工况下的悬浮隧道管体位移响应进行分析。

表4 不同工况下TMD的参数取值

以80 km/h的行车速度为例,图7描述了四种工况下,SFT管体的竖向最大位移包络线。从图7可得,安装分布式TMD之后,除0～300 m范围内的个别位置外,其余位置的管体竖向位移均显著减小,减振范围较单个TMD时得到了较大的提高,几乎涵盖整个SFT管体。这是由于在移动荷载作用初期,TMD的振幅很小,单位时间内转化的动能很少,并没有真正开始工作。

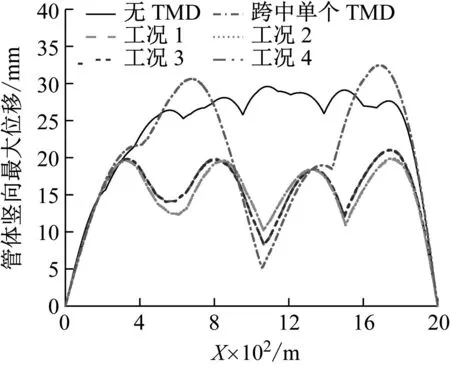
图7 不同工况下管体最大竖向位移包络图

为了更直观地说明不同工况下TMD的减振效果。图8给出了管体不同位置处TMD的减振率。由图8可得,分布式TMD相较于跨中单个TMD,L/2处的减振率降低了约10%～15%,但L/4, 3L/4处的减振率大幅提高。对比工况1、2或工况3、4可发现,TMD频率取安装位置对应的管体自振频率时,其减振率比都取管体一阶频率的减振率更高。对比工况1、3或工况2、4可发现,所在位置TMD的质量比越大,对应位置减振率越高。考虑设计方便等因素,可采用工况1将总质量平均分给3个TMD,以得到较高的综合减振效果。

3.3 移动速度的影响

为研究荷载移动速度对TMD减振效果的影响,图9给出了安装TMD前后悬浮隧道管体跨中最大位移随荷载移动速度的变化情况(以v=80 km/h,工况1跨中TMD为例)。

由图9可知,在未安装TMD时悬浮隧道的跨中最大挠度随移动荷载速度的提高而减小。原因是：随着荷载移动速度的提高,其在SFT管体内停留的时间缩短,共振还未充分发展之前荷载已经离开了SFT。安装TMD后,管体在不同速度移动荷载作用下最大位移相差不大,约为14 mm。与未安装TMD时相比,跨中位移均明显减小,随着荷载移动速度的增加,TMD减振效果会逐渐降低。车速为80 km/h时,减振率为50.21%,而车速为100 km/h时,减振率下降为37.77%。这是由于在单一移动荷载作用下,由于低速荷载在悬浮隧道管体中停留时间更长,TMD的作用时间越长,减振耗能过程越充分。

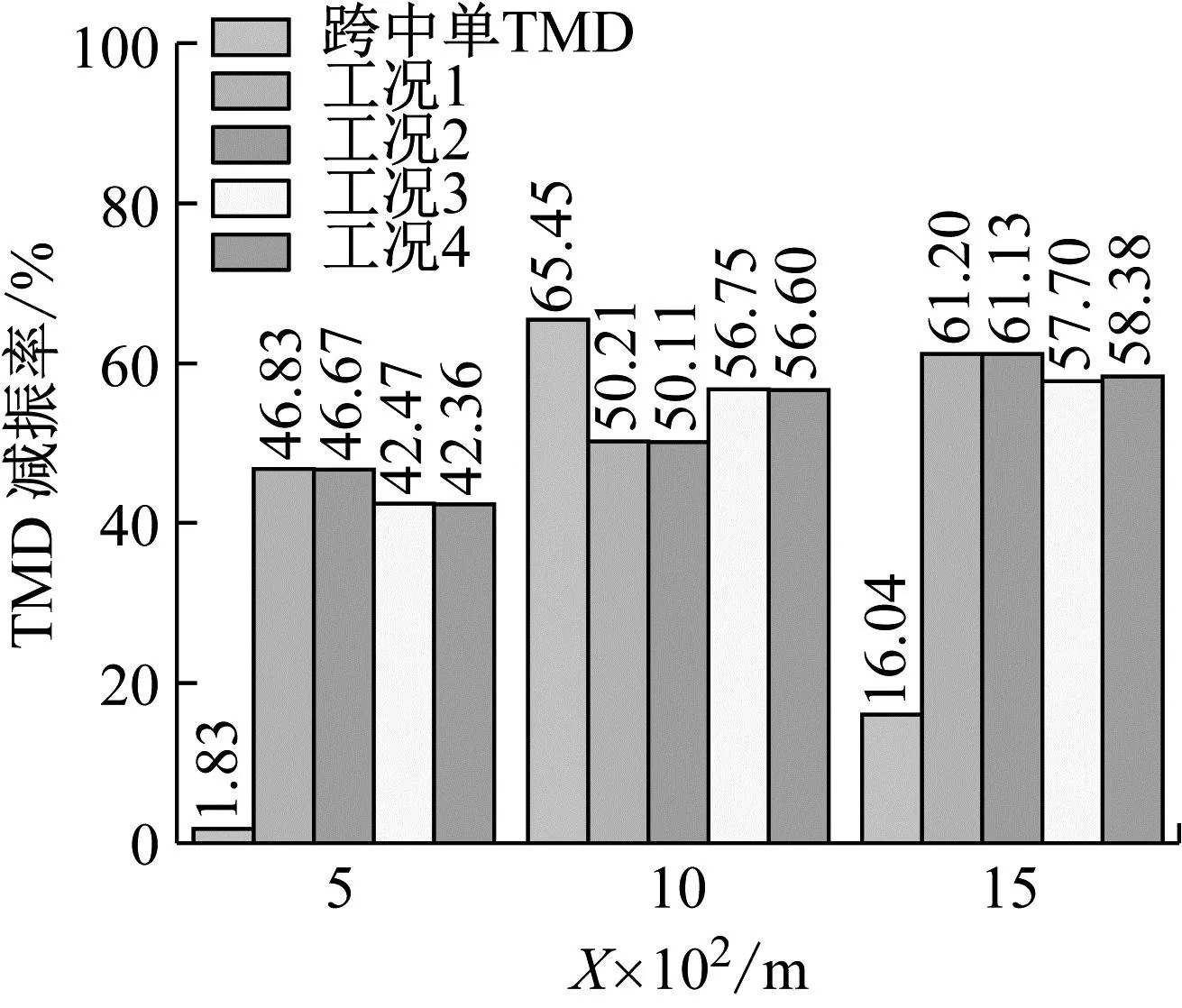
图8 管体不同位置处TMD的减振率

图9 不同移动速度下管体跨中最大位移

3.4 TMD阻尼比的影响

在研究TMD阻尼比对于减振效果的影响时,保持TMD的频率比为1.0,总质量比0.02不变。图10给出了TMD阻尼比对减振效果的影响(以v=80 km/h,工况1跨中TMD为例)。

由图10可知,TMD减振效果随着阻尼比的增加呈现减小的趋势。表5进一步给出了不同阻尼比工况下管体-TMD系统的响应情况。随着TMD阻尼比的增加,TMD质量块的峰值速度和最大行程减小,在一个振动周期内,TMD质量块吸收和转化的动能减小,管体的动能相对较大,导致减振效果减弱。但小阻尼比会使TMD的振动行程增大,对TMD系统长期工作稳定性不利,同时也需要更大的工作空间。因此,在确定TMD阻尼比时,需综合考虑减振效果以及系统的工作空间。

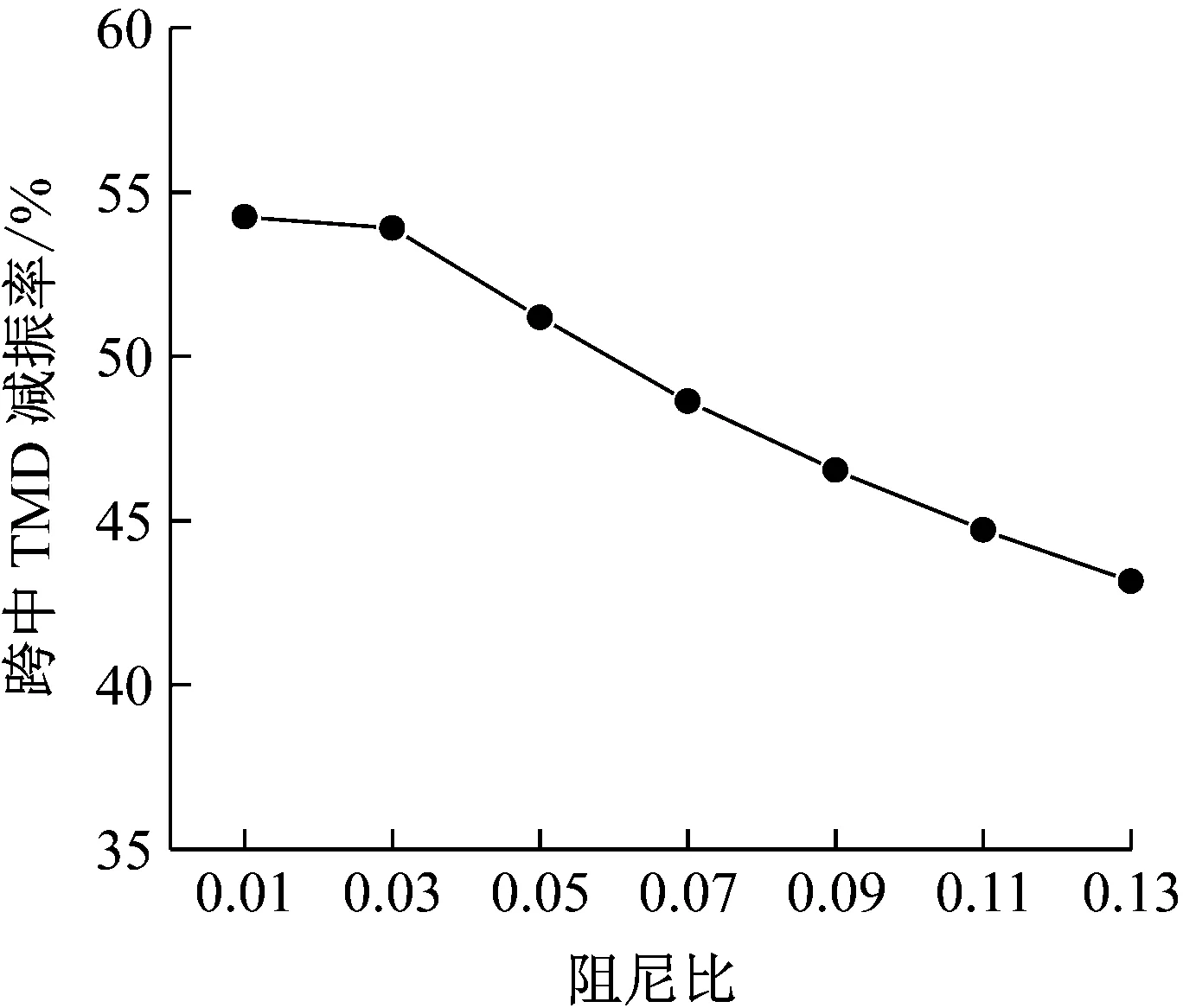
图10 阻尼比对TMD减振效果的影响

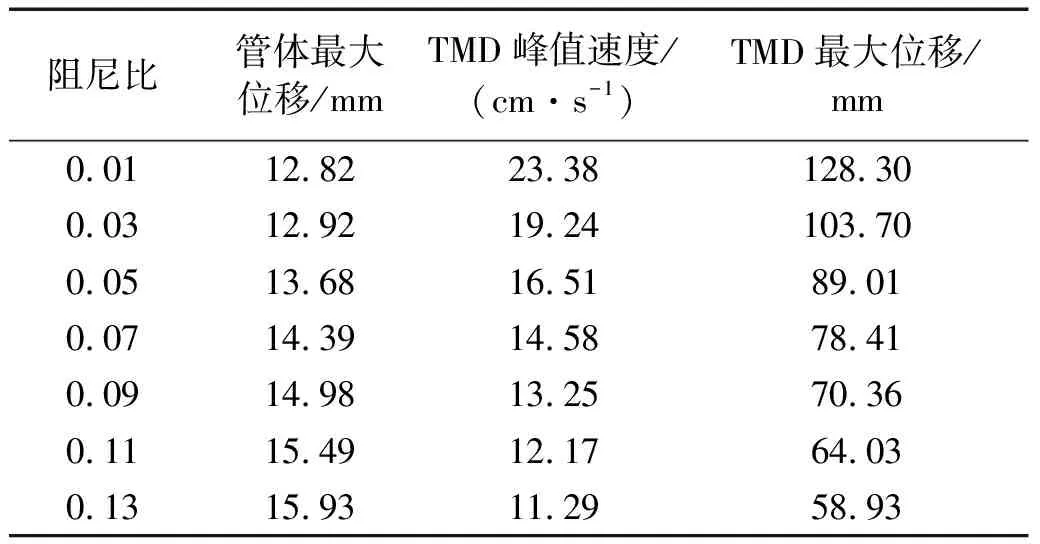
表5 不同阻尼比下SFT-TMD系统的响应

4 结 论

为实现移动荷载作用下悬浮隧道的TMD振动控制,本文建立了管体-TMD系统简化计算模型,基于Morison方程,考虑流体的附加惯性效应和阻尼效应,推导建立了在移动简谐荷载作用下管体-TMD系统的振动控制微分方程组,采用了Newmark-β法进行了数值求解,分析不同布置方式下TMD的减振效果和关键参数的影响,得出以下结论：

(1) 在移动简谐荷载作用下,悬浮隧道高阶模态参与振动。跨中安装单个TMD对其附近一定区域内有较好的减振效果,但减振范围有限。

(2) 在保持质量不变的情况下,采用分布式TMD的安装方式,更能适应悬浮隧道多阶模态参振的特点,能有效扩大减振范围,得到较好的整体减振效果。安装分布式TMD时,各TMD装置的质量可以均匀分配,其频率应与安装位置对应的管体自振频率一致。

(3) 随移动荷载速度降低,TMD的减振效果提高。在低速荷载作用下,TMD的反应及工作时间更为充足,在确定悬浮隧道合理车速时可予以考虑。

(4) TMD阻尼比的增加会降低减振效果,在确定阻尼比时应综合考虑减振效果和工作空间的要求。