考虑挠度的宽温域陶瓷轴承转子系统动态特性分析

白晓天, 杨武哲, 王子男, 郑 浩

(沈阳建筑大学 机械工程学院,沈阳 110168)

滚动轴承是许多机械装置的基本组成部件,其动态特性对于整个机械系统而言至关重要。在航空航天、核电、超高速机床等高精尖领域极端工况下,传统钢质轴承服役性能不能满足要求。全陶瓷球轴承具有密度小、抗震抗热性好等优点,在各类极端工况下得到了广泛的应用[1-2]。在实际工作中全陶瓷轴承放于钢制轴承座中,由于两者热变形系数相差较大,温度升高导致外圈与轴承座间配合间隙增大,影响轴承运转精度。转子质量对轴尤其是大长细比轴产生挠度影响。宽温域情况下配合间隙增大,挠度变化对外圈的影响变得更加明显,外圈与底座间的冲击更加剧烈,对全陶瓷轴承寿命造成严重影响。因此,对全陶瓷轴承进行建模分析有助于获取不同挠度对宽温域全陶瓷轴承动态特性的影响机制,对提升轴承转子系统服役性能具有重要意义。

目前在航空航天、高速机床领域内应用的全陶瓷球轴承的振动主要源于运转过程中内部构件间的摩擦、撞击作用,与结构尺寸、工况参量等密切相关[3-6]。Shi等[7]考虑了宽温域内陶瓷轴承与钢制轴承座热变形的不同,建立了宽温域内的轴承动力学模型,计算得到了外环的运行轨道和旋转速度。靳岚等[8]对角接触球轴承的生热机理进行了分析,得到了接触参数,摩擦生热量,温升之间的相互影响关系。Bizarre等[9]建立了五自由度系统球轴承动力学模型,得到了非线性弹性流体作用下可变接触刚度与阻尼对轴承动态特性影响规律。Han等[10]基于赫兹接触理论对角接触球轴承进行分析,对不同径向作用力下滚动体打滑效应进行了分析,得出了影响打滑效应的载荷因素。Bai等[11]考虑陶瓷材料特性,研究了滚动体球径差对全陶瓷球轴承承载特性的影响情况,得出滚动体球径差对声辐射有显著影响,并随着转速增加影响更加剧烈。国内外关于挠度对滚动轴承的研究往往是基于轴承箱歪斜、轴承座不同心转子质量密切相关[12-15]。Gao等[16]考虑轴承箱挠度对圆柱滚子轴承-转子系统振动性能的影响,得到轴承箱偏转角对轴承动态特性影响规律。然而,现阶段大多数学者在轴承建模过程中,将轴承座作为刚性元件,轴承外圈坐标系作为参考坐标系[17-18],未考虑温度改变时轴承外圈与轴承座之间配合间隙的变化,或者考虑配合间隙的变化而未考虑配合间隙变化情况下转轴挠度变化对全陶瓷轴承动态特性的影响。针对这一问题,本文在建模过程中考虑配合间隙变化以及宽温域情况下挠度变化带来的影响,获得全陶瓷轴承振动幅度随温度以及挠度变化规律,并结合试验手段,对考虑挠度的全陶瓷轴承-转子系统的动态特性展开研究。

1 考虑挠度的宽温域全陶瓷轴承动力学模型建立

1.1 宽温域全陶瓷轴承动力学模型建立

对于轴承转子系统,轴承安装于轴承座中,内圈与轴固结在一起随轴旋转。外圈与轴承座之间存在配合间隙用于调整轴承轴向位置。然而,在宽温域范围内,陶瓷材料与钢材料热变形系数的不同会导致外圈与轴承座配合间隙的变化,内圈和轴之间的配合间隙呈现减小趋势,内圈和外圈配合得更紧,没有发生相对运动,不影响轴承整体动态特性,因此在文中未进行特殊计算。假设外圈与轴承座的热变形在所有方向上都是均匀的,忽略陶瓷材料的变形各向异性和边缘处发生的边界效应。轴承外圈与轴承座热变形前后的结构如图1所示。

图1 发生热变形部件

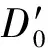
(1)

(2)

L′=L·(1+αp·ΔT)

(3)

(4)

式中：αo为陶瓷轴承外圈热变形系数;αp为钢制轴承座的热变形系数;ΔT=T-T0为温度变化范围,其中T为工作温度,T0为初始配合温度。则热变形后的配合间隙可以表示为

(5)

由于轴承外圈与轴承座发生热变形,发生热变形后,考虑配合间隙的全陶瓷轴承接触模型如图2所示。

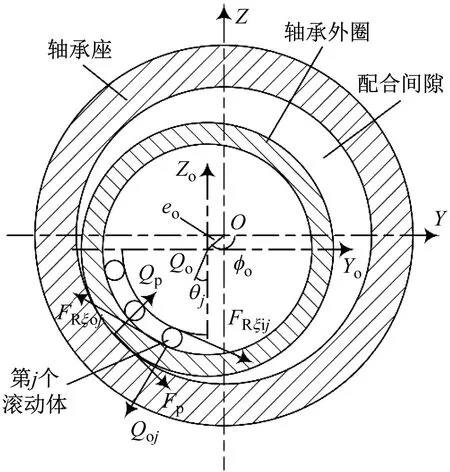
图2 考虑配合间隙的全陶瓷轴承接触模型

在图2中：{O;Y;Z}为参考坐标系;{Oo;Yo;Zo}为外圈坐标系;OY与OZ分别为轴承径向的水平与竖直方向;Oo为外圈的中心;Qoj为第j个滚动体与外圈的接触力;FRξoj为第j个滚动体与外圈的摩擦力,滚动体由内圈驱动;FRξij为内圈与滚动体之间摩擦力;θj为第j个滚动体的方位角;Qp和Fp分别为轴承外圈与轴承座的接触力和摩擦力。为了表示更为清晰,图2中未显示出内圈与保持架。轴承动力学模型中忽略了轴承座与外圈的制造误差,只考虑轴承外圈的径向运动。轴承外圈与轴承座存在配合间隙时,外圈中心Oo与轴承座中心O不一致。Oo与O之间的距离为eo,eo可以表示为

(6)

式中,yo和zo分别表示外圈中心Oo在参考系{O;Y;Z}中的位置。外圈中心Oo的方位角φo可以表示为

(7)

陶瓷材料具有比钢更高的弹性模量,陶瓷轴承相较于钢更不容易发生变形,因此认为接触变形只发生在轴承座上,对于外圈径向尺寸没有影响。这意味着只有当

(8)

外圈与轴承座发生接触,不满足条件时外圈与轴承座未发生接触。假设接触力在小变形范围内满足赫兹接触理论,则接触力可以表示为

(9)

(10)

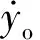
1.2 考虑挠度的轴承动力学模型

在考虑挠度的轴承动力学模型中转子两端由2个相同的全陶瓷球轴承支撑,左侧支撑端轴承动力学模型如图3所示。

图3中：mp为转子在圆盘处的等效集中质量;FL为左端轴承的支承反力;LL为左侧轴承到圆盘距离;W为转轴的挠度;θ为转轴转角。假设圆盘距左右两端轴承距离相等,通过对转轴进行材料力学性能分析,可以得到转子质量与挠度和转角的关系

(11)

(12)

式中：E为轴的弹性模量;I为轴的截面惯矩。根据平面力系静力平衡条件,可以得轴承支承反力与转子质量关系

2FLcosθ=mP·g

(13)

式中,g为重力加速度。由于转子质量对转轴产生挠度影响,从而导致转轴产生转角,此时轴承与转轴接触处产生角位移,对滚动体与内外圈的接触力产生影响。轴承内圈动力学方程可表示为

(14)

(15)

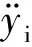
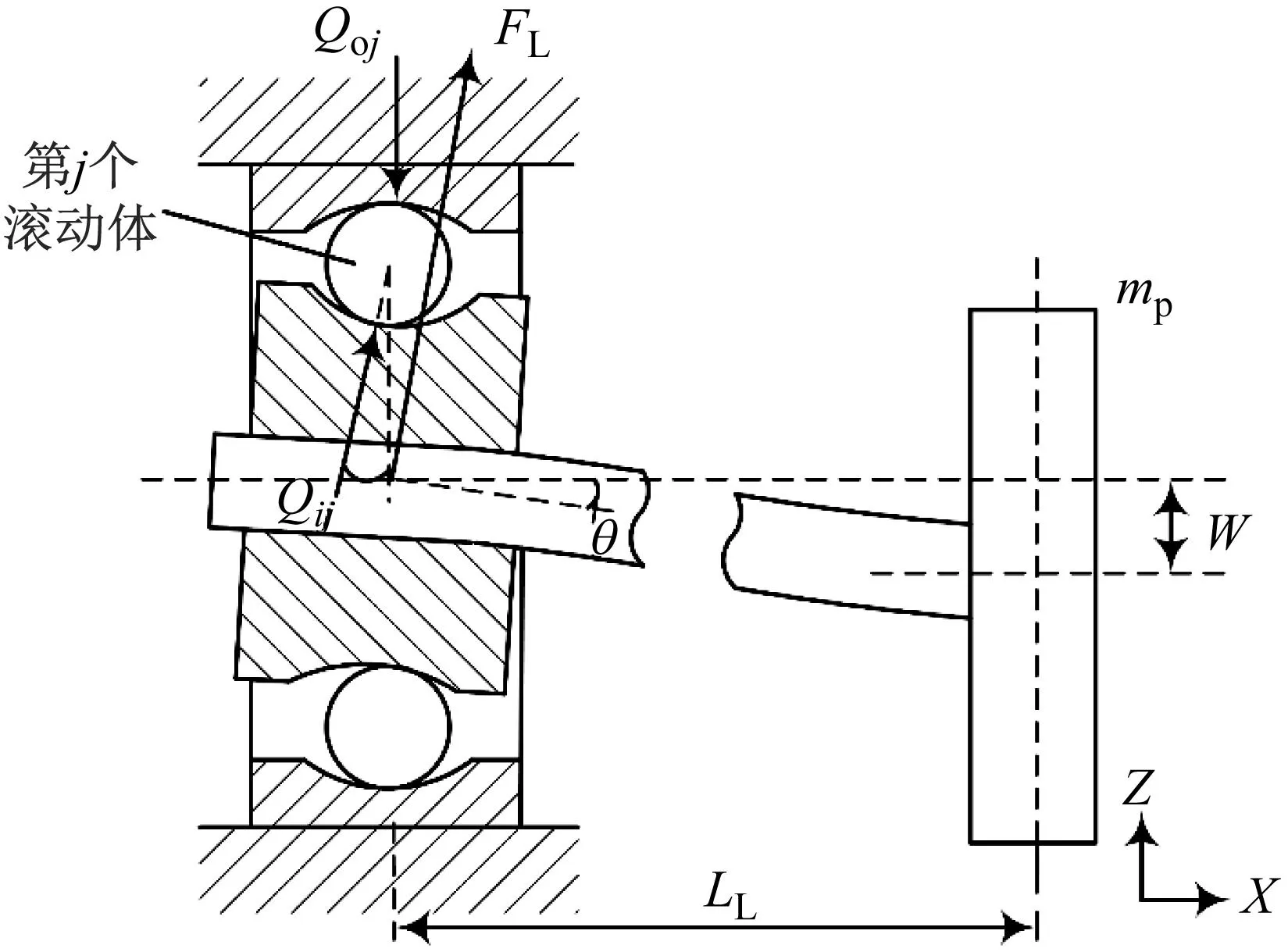
图3 考虑挠度左侧轴承转子系统模型

模型对滚动体以及保持架进行了计算,具体研究过程参考文献[19]中所使用方法。假设轴承外圈与轴承座的热变形不影响轴承轴向振动,则根据牛顿第二定律,轴承外圈动力学方程可以表示为

(16)

(17)

(18)

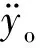
忽略轴承外圈与轴承座在不同温度下的各向异性,则在热变形过程中轴承座接触刚度保持不变,当工作温度以及转子质量发生变化时,轴承外圈的振动情况发生改变,从而对轴承的动态特性造成影响,具体所造成影响需通过仿真计算得出。

2 仿真结果与分析

全陶瓷轴承外圈与底座的热变形用式(1)～(4)表示,外圈与轴承座之间的间隙用式(5)表示。假设在初始时间t=0时,第j个滚动体的方位角φj=0,外圈中心方位角φo=0,转速ωs=1 440 r/min。

假设初始温度T0=100 K,T0温度下初始配合间隙为0.003 mm。模拟过程中全陶瓷球轴承为7009C型,轴承与轴承座主要结构参数如表1所示。轴承与转轴部件性能如表2所示。

表1 T0温度下全陶瓷轴承和轴承座几何尺寸

表2 轴承与转轴部件参数特性

2.1 宽温域内挠度对轴承动态特性影响

轴承部件之间的摩擦因数为0.1,外圈与轴承座之间的摩擦因数为0.2,转子质量10 kg。假设轴承工作时润滑良好,忽略速度波动的影响,由于陶瓷材料热变形小,温度对于波纹度的影响可以忽略不计,忽略滚动体球径差异。仿真过程采用四步龙格库塔算法求解动力学方程。在工作温度T=100 K,T=400 K时,分别对考虑转轴挠度与不考虑转轴挠度的情况对外圈振动位移进行计算,根据式(9)计算碰撞力,并结合其时域结果进行分析,结果如图4所示。

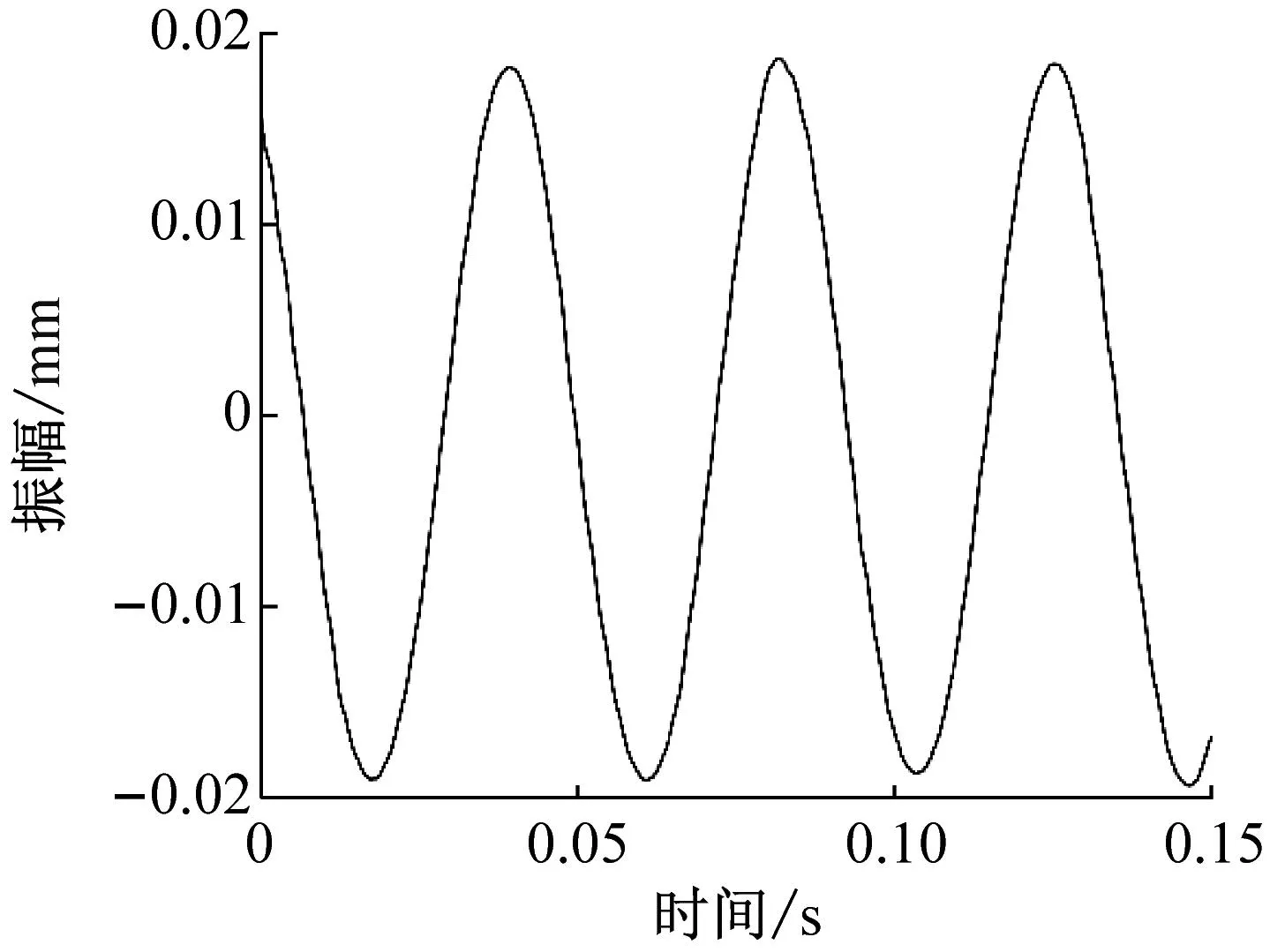
(a) T=100 K不考虑挠度

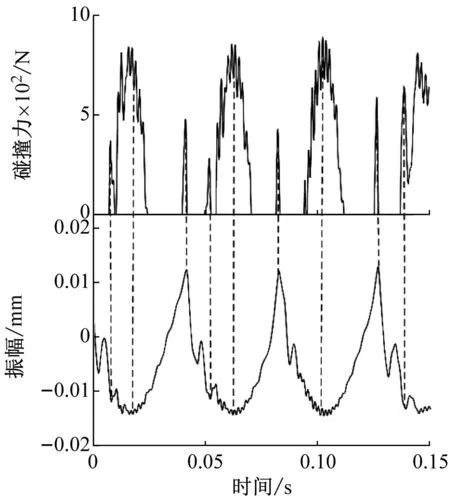
(b) T=400 K不考虑挠度

(c) T=100 K考虑挠度

(d) T=400 K考虑挠度

由图4可知,当T=100 K,不考虑挠度时,模拟信号呈现正弦规律变化,考虑挠度影响后,模拟信号出现波动,且出现碰撞力,说明外圈与轴承座发生碰撞,但此时波形仍只有一个波峰,总体为正弦趋势。当T=400 K,不考虑挠度时,由于外圈与轴承座配合间隙扩大,此时不考虑挠度的振动信号时域波形出现剧烈波动,一个周期内的碰撞力存在时间变长,幅值变大,说明由于间隙增大,轴承外圈与轴承座碰撞现象更明显;考虑挠度后,振动位移时域信号波形与不考虑挠度相比变化巨大,且一个周期内碰撞力存在时间进一步增加,碰撞力幅值变大,说明挠度会导致宽温域下的碰撞现象更加明显,此时正方向振幅几乎为0,这是因为温度增加间隙变大,考虑挠度后,离心力无法克服轴承自身重力以及转子质量的影响,导致轴承无法沿轴承座孔爬升至顶端,轴承趋于在轴承座孔下半部分运行。通过快速傅里叶变换分析其频域结果,如图5所示。

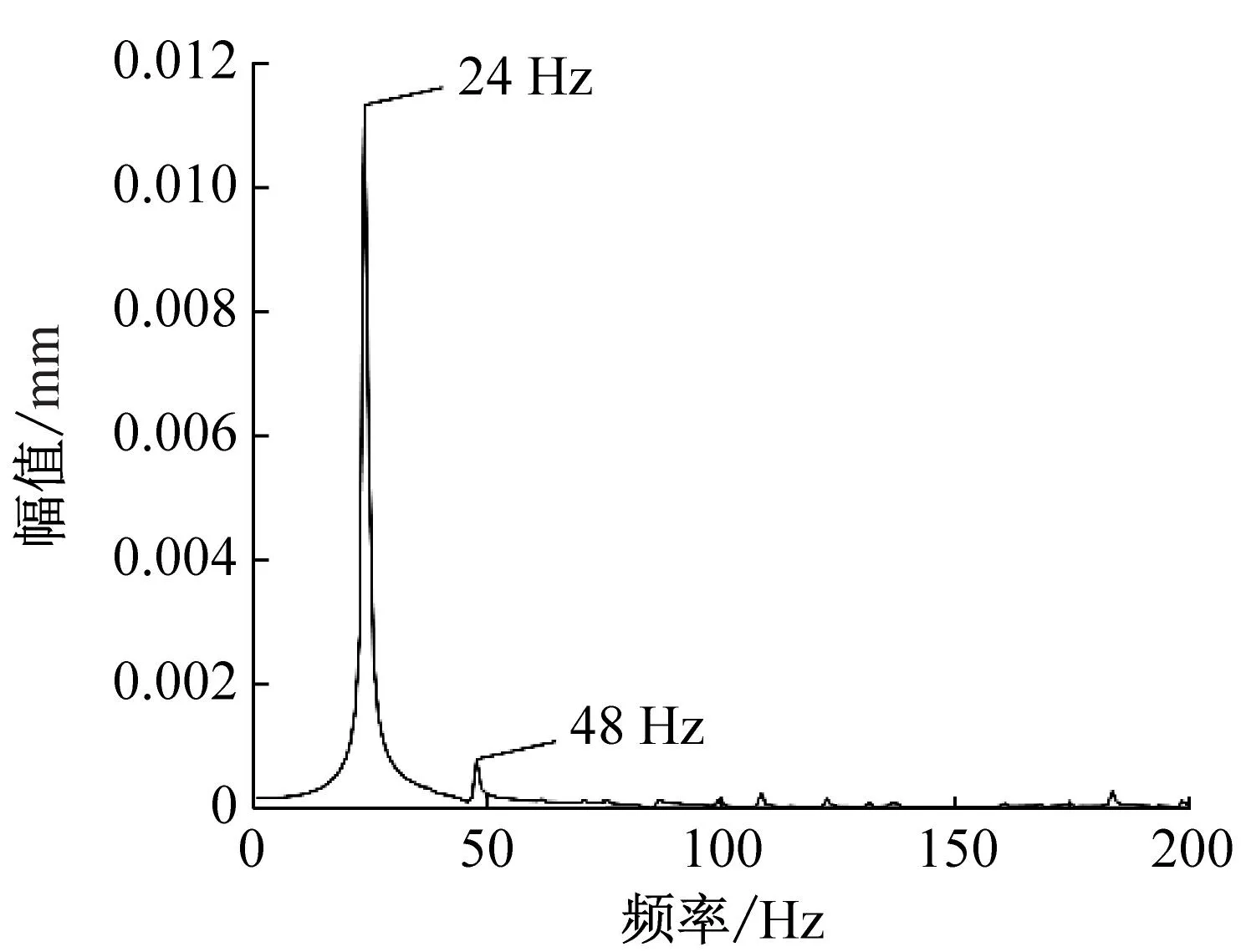
(a) T=100 K不考虑挠度

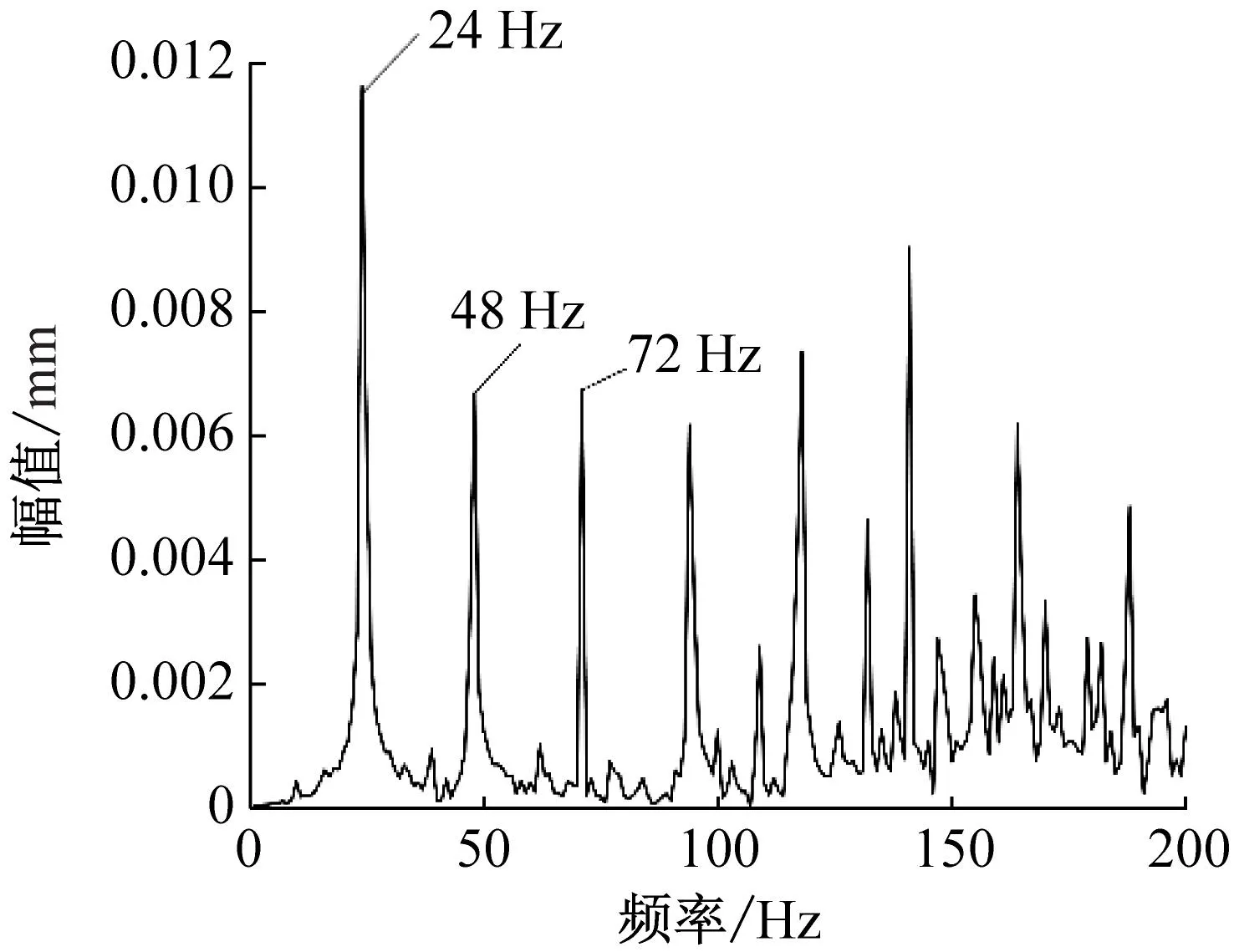
(b) T=400 K不考虑挠度

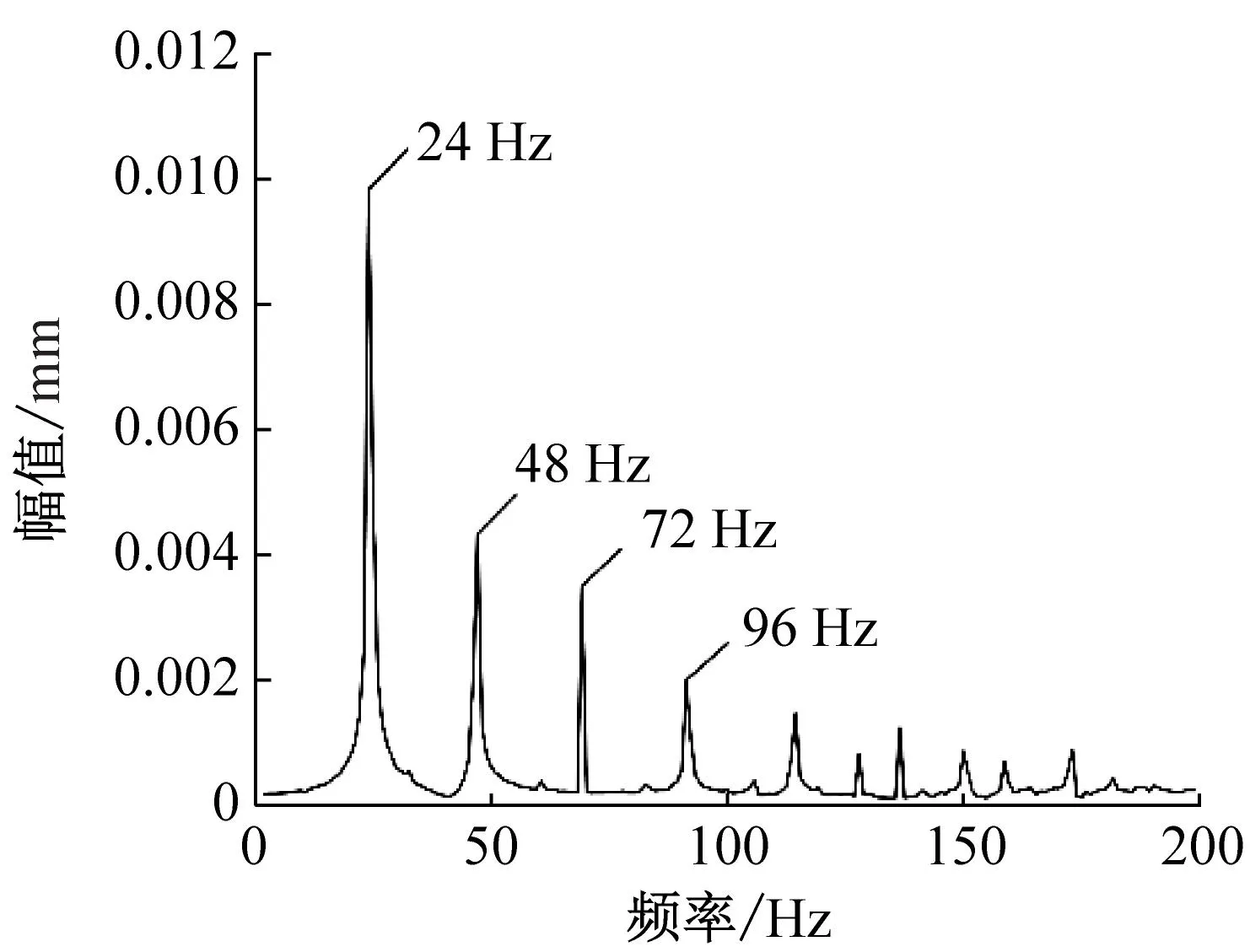
(c) T=100 K考虑挠度

(d) T=400 K考虑挠度

由图5可知,在100 K温度下,不考虑挠度时,频域图中存在24 Hz、48 Hz频率成分,分别为转频的1、2倍频;考虑挠度因素后,频域图中除1、2倍频外,3倍频72 Hz、4倍频96 Hz幅值升高,此时转频仍然为主要成分。400 K温度下,温度升高,轴承外圈与轴承座配合间隙增加。不考虑挠度时,高频部分出现谐波频率,转频及其倍频仍然占据主要成分,3倍频后出现了若干个更大的峰值,是由于温度为400 K,相较于初始温度已升高许多,因为陶瓷轴承与轴承座孔发生热变形程度不同,此时轴承松动状态严重,导致出现高频谐波成分;考虑挠度后,频域图中出现57 Hz、80 Hz、103 Hz,分别为2.3、3.3、4.3倍频,说明此时频域图出现1/3倍频,出现明显的松动特征。说明温度升高,挠度因素会导致轴承松动程度增加,因此需研究挠度对轴承动态特性的影响。

2.2 挠度影响参数化分析

由于宽温域条件下,陶瓷轴承与钢制轴承座之间配合间隙出现较大变化,在这种情况下相较于钢制轴承,转轴挠度对于陶瓷轴承动态特性的影响更大。在温度较高的情况下轴承处于松动状态,轴承外圈中心Oo趋于在轴承座孔下方运动,此时挠度对于轴承转子系统动态特性产生影响,本节将研究转轴挠度对于轴承动态特性的影响。

在T=200 K时,陶瓷轴承外圈与轴承座间隙发生变化,此时温度对于位移振动信号存在影响但影响较小。因此选择在T=200 K的情况下,分别选取转子质量为10 kg、20 kg、30 kg、40 kg,其他参数与之前一致,通过对外圈振动位移以及碰撞力进行计算,分析其时域结果,结果如图6所示。

由图6可知,在位移到达最小值时有较大的碰撞力,判断外圈与轴承座发生碰撞,在质量增加造成转轴挠度增加过程中,位移信号波动的剧烈程度逐渐增加,碰撞力存在时间与幅值增加。在转子质量较小时,振动位移信号基本呈现正弦信号规律,但随着质量的增加,时域信号发生不规则变化,信号波动更加明显,碰撞力发生时间与幅值增加,说明轴承外圈与轴承座碰撞现象更加剧烈。并且挠度增加,正方向幅值逐渐减小,40 kg时正方向振幅几乎为零,说明此时外圈趋于轴承座下半部分运动。轴心轨迹图可以体现轴承外圈整体运动情况,外圈中心的轨迹对与外圈运动的研究至关重要,外圈中心Oo的轨迹如图7(a)～(d)所示,外圈与轴承座碰撞力分布如图7(e)所示。

(a) 10 kg

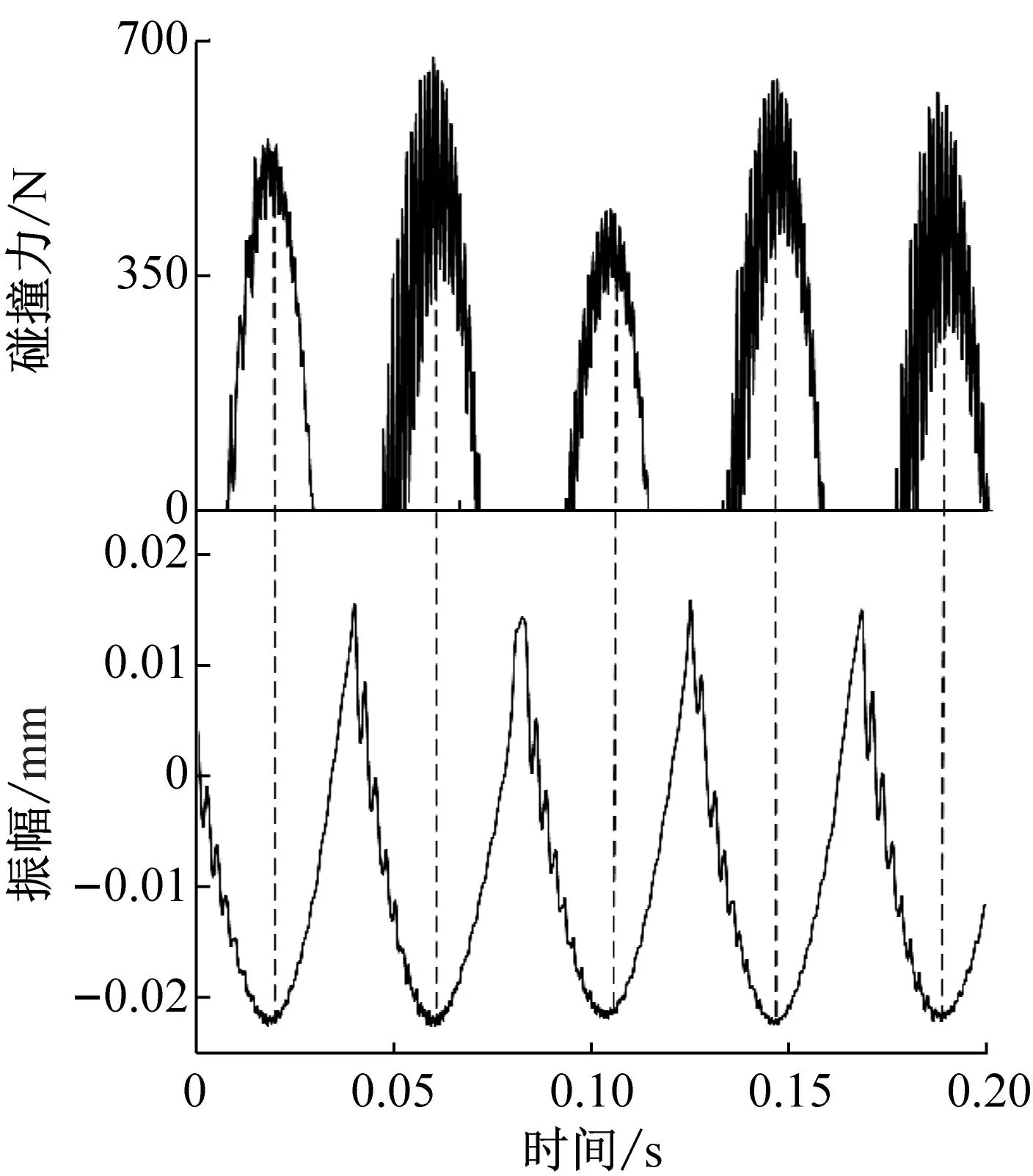
(b) 20 kg

(c) 30 kg

(d) 40 kg

由图7可知,在转子质量10 kg时,外圈中心Oo轨迹近似圆形,说明此时外圈运动覆盖整个轴承座孔。但随着质量增加,轴心轨迹出现不规则部分。从图7(e)中发现,外圈运动至下半部分存在碰撞力,说明轴承与轴承座发生冲击,碰撞力幅值以及发生的角度范围随质量增加,说明轴承与轴承座的冲击变得更加剧烈。质量从10 kg增加到40 kg过程中,挠度逐渐增大,OZ方向上振动位移幅值变化越发明显,轴承外圈运动变得更加不规则,轴承外圈在OZ正方向的振动位移幅值明显减小,质量达到40 kg时,轴心轨迹正方向运动几乎为零,轴承趋于在轴承座底部涡动。这是因为在挠度较小时,离心力可以克服转子质量所带来重力影响,但随着转轴挠度增加,滚动体与内圈的接触力减小,同时离心力于竖直方向的分力减小,并且转子重力的增加,离心力与接触力逐渐无法克服增加质量的影响,导致轴承无法运动至轴承座上半部分,此时轴承外圈几乎紧贴轴承座下半部分,轴承趋于在轴承座孔底部涡动。

(a) 10 kg

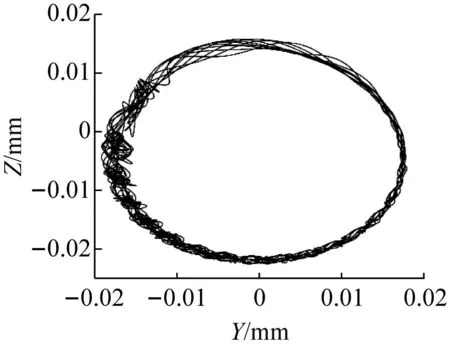
(b) 20 kg

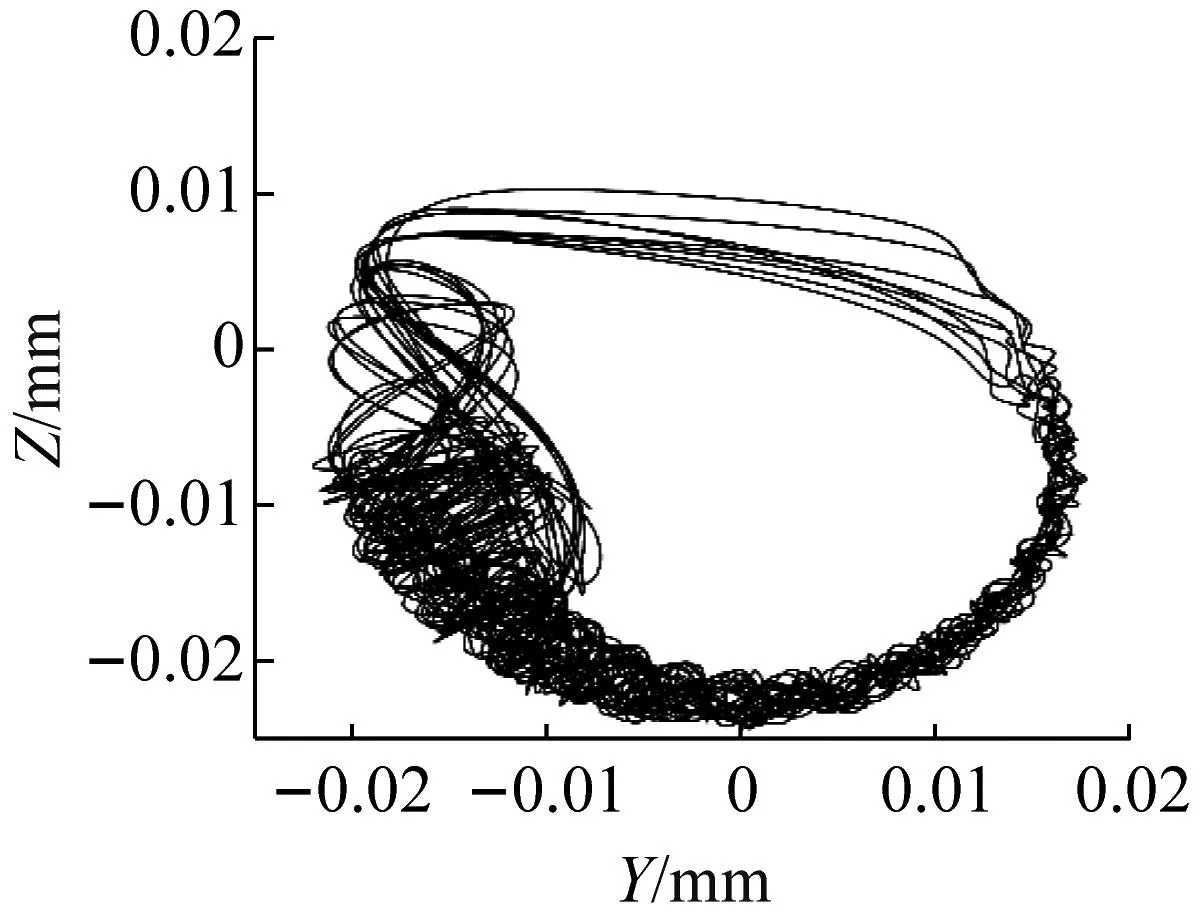
(c) 30 kg

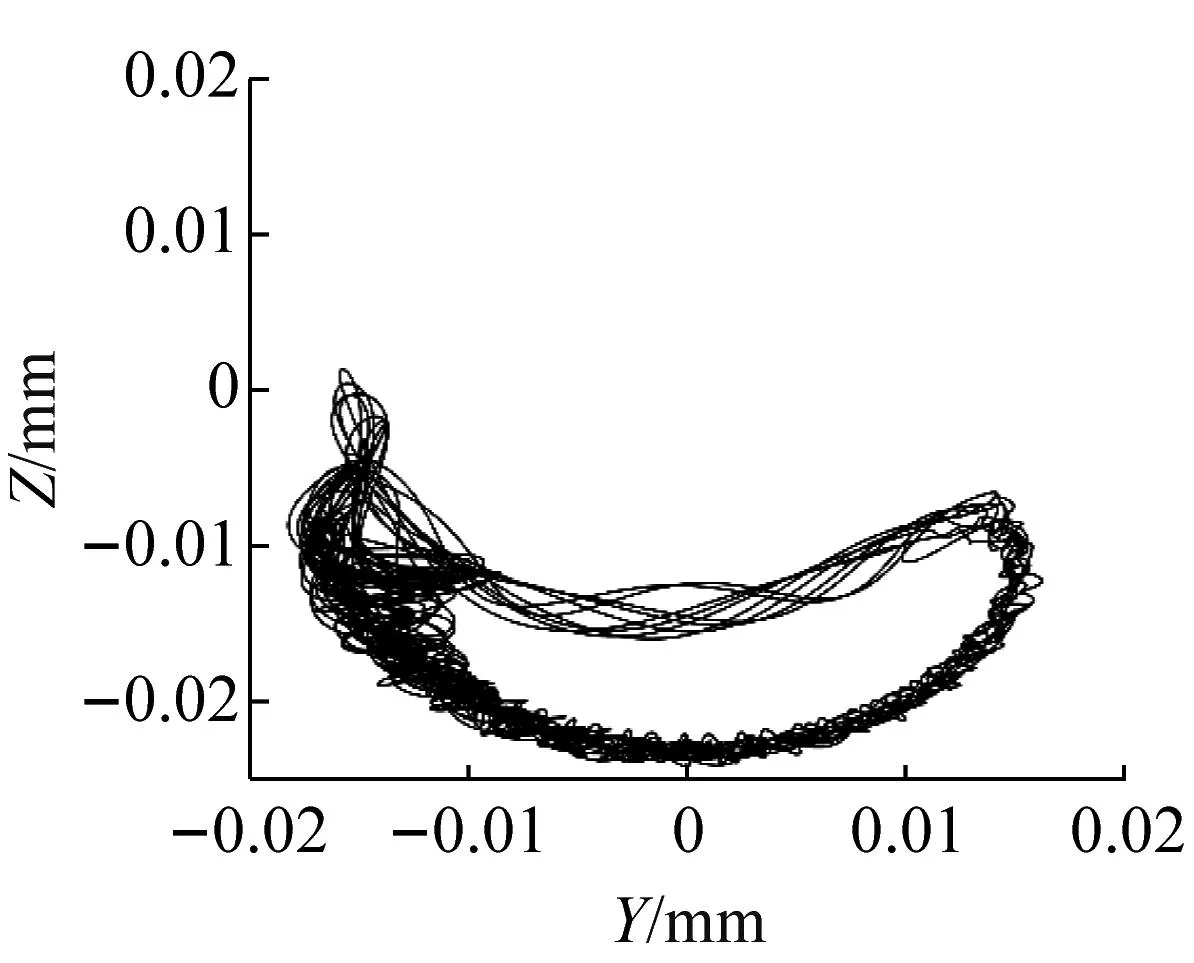
(d) 40 kg

(e) 不同质量下碰撞力分布图

3 试验验证

采取试验手段对全陶瓷球轴承转子系统不同温度以及不同挠度下动态特性进行测试。在实验室环境下,采用液氮冷却的方法获取其低温升至室温过程中的振动情况,通过电加热装置来获得高温情况下的振动数据。试验在轴承试验机上进行,使用保温箱控制轴承工作温度,通过改变旋转圆盘的质量来改变转轴挠度,图8为本试验中使用的轴承-转子试验台。

设定转子转速为1 000 r/min,工作温度为300 K,转子质量为10 kg,轴承型号为7009C型。采用接触式传感器测量全陶瓷轴承径向振动数值,将采集到的振动位移数据进行傅里叶变换,得到该挠度下轴承外圈振动位移频域结果。根据式(16)～(18),分别通过计算得到在温度100～600 K、转子质量10～60 kg、转速600～3 000 r/min的不同条件下仿真结果,选择与试验条件相同的仿真结果,将考虑转轴挠度、不考虑转轴挠度频域结果与试验结果进行对比,结果如图9所示。

图8 试验装置图

图9 仿真计算结果与试验结果对比

由图9可知,在陶瓷轴承与轴承座存在间隙的情况下,不考虑挠度时轴承外圈振动频谱主要为转频成分,倍频成分不明显。考虑转轴挠度后,频域图中出现转频的整数倍频,说明轴承径向振动增大。试验结果表明,宽温域下,考虑转轴挠度的计算结果与试验测量结果的幅值与频率差距均较小,说明考虑转轴挠度的宽温域陶瓷轴承动力学模型计算精度较高,可用于宽温域全陶瓷轴承转子系统动态特性的计算。根据前文仿真结果与试验结果可以推断,挠度增大会使轴承倍频成分更加明显,轴承振动增大,宽温域情况下,挠度增加使得轴承的松动程度增大,使轴承转子系统不稳定。在陶瓷轴承转子系统设计过程中需考虑不同转轴挠度对其回转精度的影响。

4 结 论

(1) 温度升高,转轴挠度使轴承外圈松动现象增加。温度从100 K变化为400 K,考虑挠度相较于未考虑挠度,频域信号出现1/3倍频信号,出现松动特征,说明挠度对宽温域陶瓷轴承松动现象增加。

(2) 宽温域情况下,随着挠度增加,全陶瓷轴承外圈运动范围减小。转子质量增加,挠度增大,外圈竖直方向位移逐渐减小,40 kg时,外圈紧贴轴承座下方运动,说明轴承转子系统不稳定。

(3) 通过与试验结果对比,说明考虑挠度因素的动力学模型能够更好的描述全陶瓷轴承转子系统运动状态。在宽温域下,应选用较小转子质量以减小挠度对轴承动态特性的影响。