含不平衡质量弹性边界约束旋转梁结构振动特性分析
和飞帆, 杜敬涛, 赵雨皓, 刘 杨
(哈尔滨工程大学 动力能源工程学院,哈尔滨 150001)
转轴(旋转梁)作为机械设备的重要部件,被广泛用于航天、船舶、车辆等众多工程领域。机械设备的运行寿命、机械效率、振动噪声等指标与旋转部件的动力学特性紧密相关,保证转轴的稳定运行是工程机械正常工作的前提。转轴运行时振动特性受到许多因素的影响,如受到流场激励载荷、轴向载荷,与机体发生碰撞摩擦,长时间高强度工作产生疲劳裂纹,磨损的轴承等。为了有效降低、避免转轴结构在上述外部载荷激励、边界约束条件下的非正常振动,掌握转轴的振动特性显得尤为重要。所以研究含不平衡质量弹性边界约束下的旋转梁结构振动特性对转轴优化设计、故障诊治等具有重要意义。
国内外学者为优化旋转机械结构以及解决各种故障,使用了不同模型、方法对转轴的动力学行为与振动特性展开大量研究[1-3]。Xiao等[4]采用有限元法将Timoshenko旋转梁模型与Euler-Bernoulli旋转梁模型进行对比,分析了弹性边界条件下变截面转轴的横振、扭振、纵振。Ma等[5]建立了摩擦条件下的转子有限元模型,研究冲击激励与不平衡激励作用下转子系统的动态特性。Mao等[6-7]采用修正Adomian分解法动态分析了纵向旋转梁及阶梯梁,该方法具有收敛快、精度高等特点,且可以有效预测非经典边界条件下旋转梁的振动特性。Banerjee等[8]采用Wittrick-Williams算法研究了旋转复合梁的弯曲-扭转耦合振动效应,在研究薄壁复合梁的谐振问题中有良好效果。Pai等[9]建立垂直放置的旋转梁模型并考虑其几何非线性,准确揭示了重力、回转惯量等对旋转梁临界转速的影响。Wang等[10]采用Jeffcott转子模型研究在气体泄露的转子密封系统中,同时承受剪切应力、气体压力作用下的转子非线性振动特性。钱新等[11]采用Hamilton原理推导了以Rayleigh旋转梁为模型,在重力场以及简支边界条件下,陀螺效应对转轴临界转速等特性的影响。黄意新等[12-13]通过Chebyshev谱方法建立了弹性支承边界条件下旋转Timoshenko梁的动力学方程,获得了旋转梁各阶涡动临界转速以及模态振型。上述学者采用了振动力学经典分析方法预报了转轴、转子、旋转梁等系统的运动学特性,为了更加高效分析转轴等系统振动特性,研究者引入傅里叶级数到结构振动的分析中[14-15]。
Li[16]提出将梁的横向位移展开为傅里叶级数与辅助多项式叠加的形式,克服了标准傅里叶级数在边界处不连续问题并可便捷、系统地得到梁的模态参数。Du等[17-18]使用改进傅里叶级数表示出矩形板的面内振动,探究了不同边界约束条件对板结构振动特性的影响。Xu等[19-20]使用改进傅里叶级数分析任意变截面弹性约束杆的纵向振动,并建立了任意边界条件弹性杆扭转振动特性预报模型,研究了该方法收敛性与精确性问题。鲍四元等[21]鉴于改进傅里叶级数的广泛适用性,使用瑞利-里兹法研究连接地基的经典边界梁。赵雨皓等[22-23]研究轴向载荷作用下弹性支承梁的横向振动特性,并采用Galerkina截断法预报含非线性支承梁模型在外激励作用下的非线性运动学行为。
本文在前辈研究者的基础上,建立以Rayleigh梁为模型含不平衡集中质量、弹性边界约束以及轴向载荷的旋转梁动力学模型,结合改进傅里叶级数推导出转轴横向振动运动学方程组,研究边界支承刚度、轴向载荷对转轴正反向临界转速的影响,分析不平衡集中质量影响转轴横向振动幅频特性的变化规律。
1 理论模型
本文旋转梁模型如图1所示,单位转轴dz有两个平面xoz、yoz内的横向位移wx、wy和转动角度θx、θy共四个自由度,转轴模型为计入转动惯量的Rayleigh旋转梁模型。转轴端部分别连接xoz平面和yoz平面两个方向的平动约束弹簧和旋转约束弹簧来模拟转轴端部的任意约束状态,约束弹簧的平动刚度分别为Kx0、KxL、Ky0、KyL,旋转刚度分别为Gx0、GxL、Gy0、GyL,平动约束弹簧和旋转约束弹簧在转轴上对应的位置如图2所示。转轴模型的长度为L,半径为R,横截面积为A,密度为ρ;E为转轴模型的弹性模量,Id为转轴模型的惯性矩,Ip为转轴模型的极惯性矩;P0为转轴的轴向载荷,Ω为转轴绕z轴正方向旋转的转动角速度;m0为转轴不平衡集中质量,r为集中质量的偏心距,该集中质量作为转轴的外激励。转轴为水平方向放置,且是细长轴,忽略转轴自重对振动的影响。
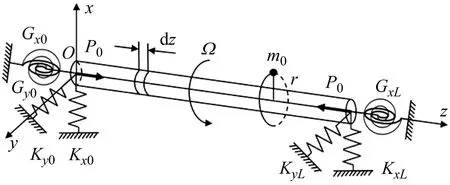
图1 弹性边界条件转轴横向振动分析模型
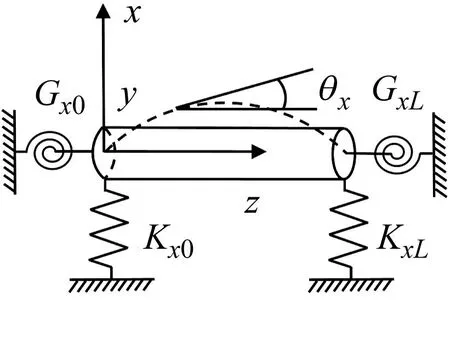
(a) xoz平面
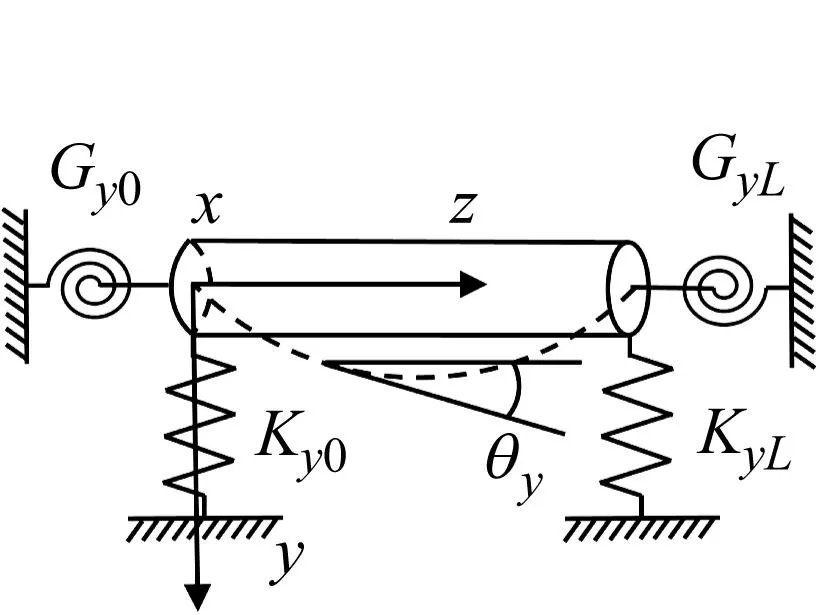
(b) yoz平面
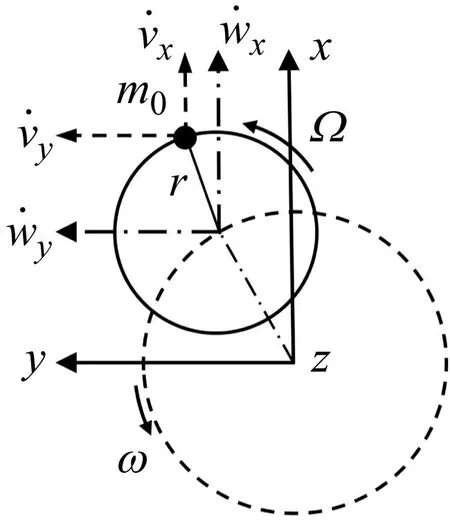
图3 不平衡集中质量运动图
本文所研究的单位转轴刚体,既有随质心的平动,又有相对于质心的转动,故使用Rayleigh旋转梁作为模型,转轴系统横向振动的总动能为
T=T1+T2+T3+T4
(1)
式中,T1为转轴平动动能,其表达式为
(2)
T2为转轴定轴转动动能,其表达式为
(3)
T3为转轴陀螺力矩项,其表达式为
(4)
式中,α、β分别为单位转轴绕坐标轴x、y正方向旋转转角[24]。θy数值上与-α相同,θy转角方向为单位转轴刚体绕x轴负方向旋转;θx数值上与β相同,θx转角方向为单位转轴刚体绕y轴正方向旋转[25]。
T4为转轴不平衡集中质量所具有的动能,由于不平衡集中质量在轴向有确定位置,即在空间上具有高度集中的脉冲性质,为了将该动能作用于连续方程中,引入狄拉克(Dirac)分布函数δ(z)。则不平衡集中质量所具有动能的表达式为
(5)
式中:m0为集中质量;zm为不平衡集中质量在转轴的轴向位置;vx、vy分别为不平衡集中质量在xoz、yoz平面内相对于转轴形心的相对速度。
转轴系统横向振动总势能为
V=V1+V2+V3+V4
(6)
式中,V1为转轴横向振动的应变能,其表达式为
(7)
V2为转轴端部平动约束弹簧的弹性势能,其表达式为
(8)
V3为转轴端部旋转约束弹簧的弹性势能,其表达式为
(9)
V4为轴向载荷P0对转轴结构势能的影响,其表达式为
(10)
2 振动方程及改进傅里叶级数
2.1 转轴横向振动方程
使用假设形态法对连续的转轴横向振动方程进行离散处理,方程中包含转轴轴向位置z、时间t两个自变量,对转轴横向位移表达式进行分离变量处理后,转轴稳态振动横向位移表示为
(11)
式中:Φx(z)、Φy(z)为1×N的矩阵;qx(t)、qy(t)为N×1的矩阵;Φx(z)、Φy(z)分别为转轴在xoz、yoz平面内的假设阵型基阵;qx(t)、qx(t)分别为转轴在xoz、yoz平面内的时间许可函数基阵,也是假设模态方法中的广义坐标项。将式(11)分别代入转轴系统的动能、势能方程中得到转轴横向振动动能、势能矩阵方程,如方程组(12)所示。
(12)
转轴系统Lagrange函数的表达式如下
L=T-V
(13)
将式(12)中的动能、势能代入式(13)中得到Lagrange函数,再将Lagrange函数代入第二类朗格朗日方程(14)得到转轴系统横向振动方程组(15)。
(14)
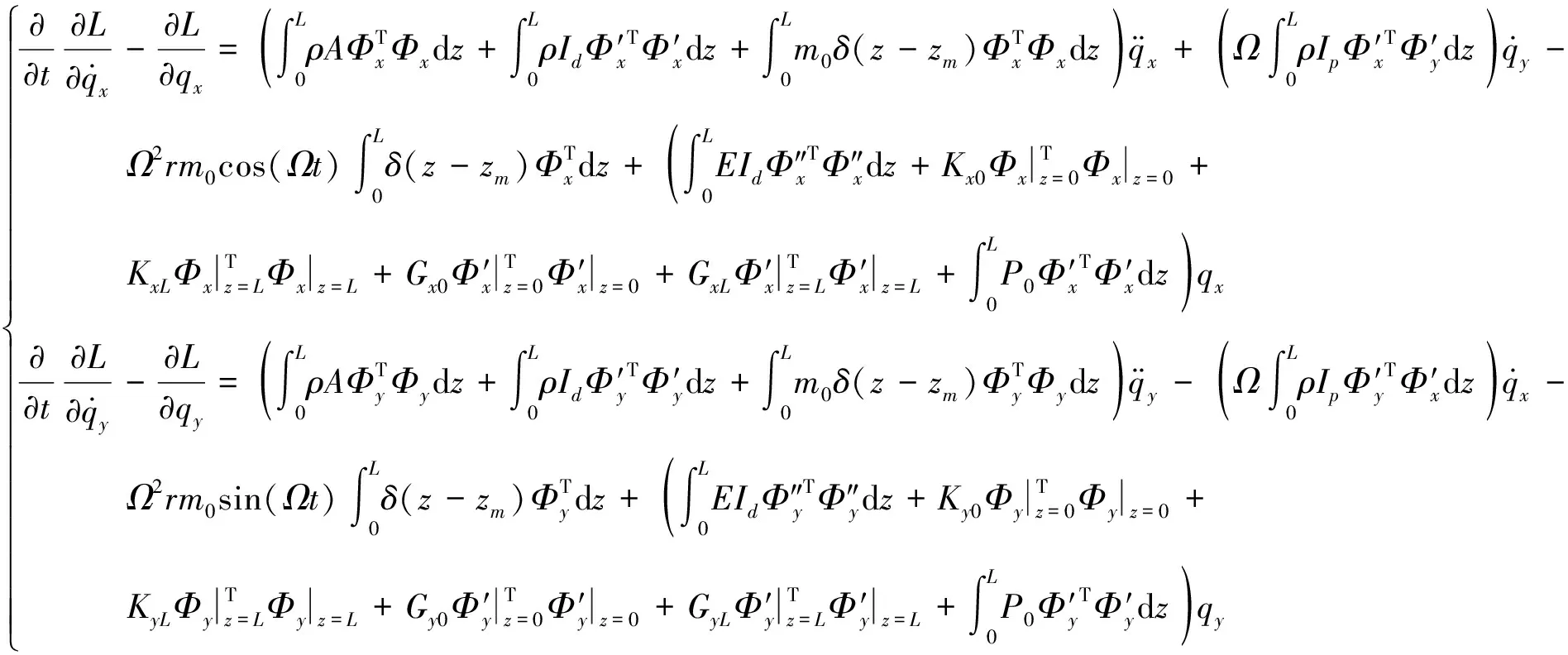
(15)
在使用第二类朗格朗日方程求得转轴系统横向振动方程组(15)中,其方程组包含两个方程,分别是转轴在xoz、yoz平面内的横向振动方程。由于本文研究对象为转轴,其端部轴承支撑刚度具有各向同性,将各向同性轴承简化为两个平面的弹簧约束。所研究不同平面内的平动约束弹簧、旋转约束弹簧刚度分别相同,即Kx0=Ky0、KxL=KyL、Gx0=GxL、Gy0=GyL。本文所研究的转轴截面为圆形,若转轴截面为矩形,则本文以下方法不能完全适用。在以上条件下,转轴在两个平面内的假设阵型相同,即Φx(z)=Φy(z)=Φ(z)。两个平面的位移函数改写为指数形式如下所示
w(z,t)=wx(z,t)+iwy(z,t)=Φ(z)Qeiωt
(16)
式中:Φ(z)为转轴横向振动位移分布函数,即假设阵型;Q为时间项的系数矩阵;e为转轴稳态振动时的时间因子;为圆频率。
将式(16)代入转轴系统横向振动方程组(15)中可将两个方程合写为一个方程,在这里先不记入不平衡集中质量对转轴运动方程的影响(m0=r=0),最终转轴横向振动矩阵方程如(17)所示。该方程成立的前提是只分析转轴稳定振动的状态,假设其稳定振动的轴心轨迹为圆形。
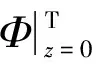
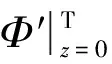
(17)
2.2 以改进傅里叶级数为假设形态的模型
将转轴横向振动位移分布函数(16)使用余弦级数和辅助函数展开后,改进傅里叶级数表示为[26]
w(z,t)=Φ(z)Qeiωt=
(18)
式中,Φ(z)的具体表达式为
(19)
式中,ξm(z)(m=1,2,3,4)为傅里叶级数辅助函数,其具体形式如下
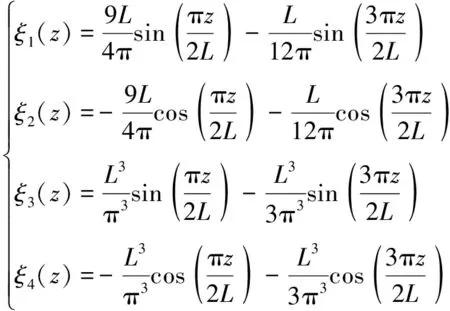
(20)
对于边界是任意约束条件下的转轴结构来说,其横向振动的位移分布函数可以采用改进傅里叶级数方法进行展开。该方法是在传统傅里叶余弦级数的基础上增加四项傅里叶级数辅助函数,展开的余弦级数是标准展开傅里叶级数数量的一半。若只有余弦级数展开项,则横向振动位移分布函数在边界上各级的奇数阶导数恒等于零,即位移分布函数展成余弦级数后在边界处不连续,不符合转轴实际运动状态,所以需要引入辅助函数项。引入辅助函数项后,以z=0和z=L边界处的辅助函数为例,容易证明:
(21)
式(21)表明在边界上,辅助函数的一阶和三阶导数均等于一,傅里叶余弦级的一阶导数和三阶导数均等于零,从而成功克服了位移分布函数展成余弦级数在边界上的不连续性,同时该方法有较快的收敛性并保证了良好的精确度。最终将位移分布函数Φ(z)(19)代入式(17)中对转轴系统的横向振动特性进行数值计算及分析求解。
3 数值计算及结果分析
本文所选用转轴系统参数如表1所示。
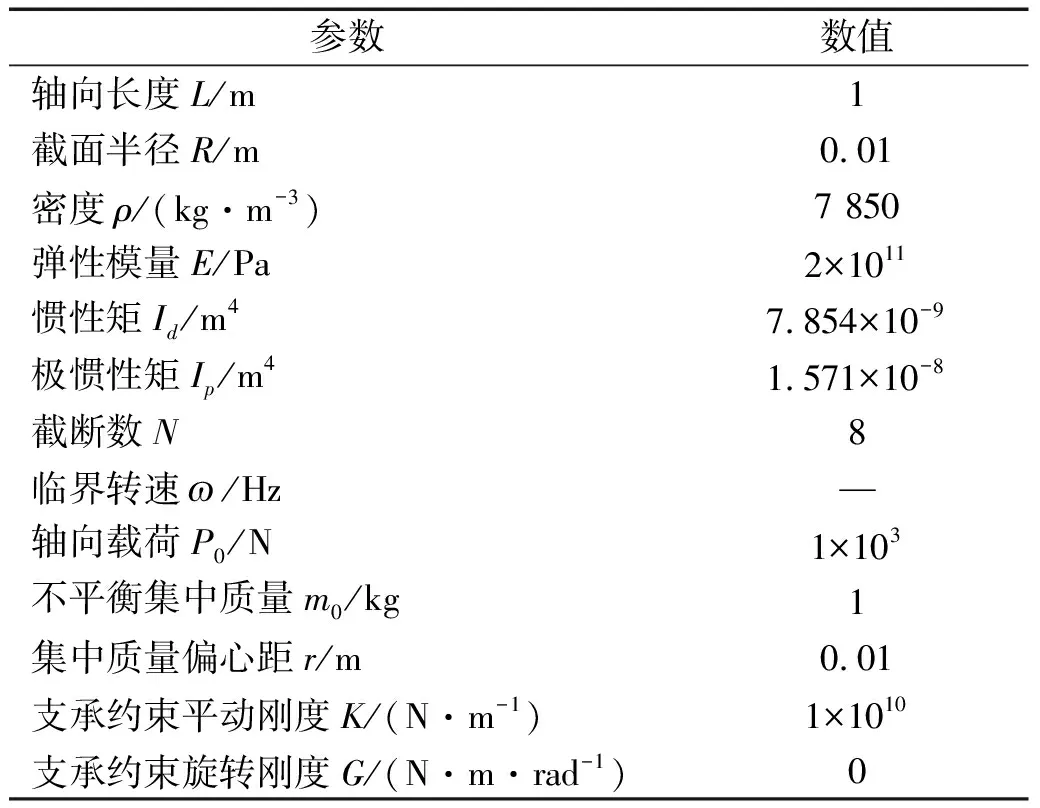
表1 转轴系统几何参数和物理参数表
3.1 方法收敛性与精确性
3.1.1 改进傅里叶级数方法收敛性分析
本节研究改进傅里叶级数方法的收敛性,以无集中质量的简支转轴为例,轴向载荷取P0=1 000 N。
由表2分析可得,在以改进傅里叶级数为位移分布函数的转轴系统中,横向振动的正反向临界转速随着改进傅里叶级数的截断数增大而趋于稳定。转轴系统横向振动的前三阶正反向临界转速在截断数取四时已趋于稳定,而转轴系统横向振动的第四阶、第五阶正反向临界转速在截断数取八时趋于稳定。由此可得改进傅里叶级数方法的收敛速度较快,在转轴横向振动矩阵方程推导运算中,该方法可缩小矩阵的维度从而加快矩阵的求解速度。
3.1.2 对比解析法
将改进傅里叶级数与传统解析法求得的转轴正反向临界转速进行对比,转轴系统两端边界条件与上小节相同。
由表3可以得出,本文改进傅里叶级数法计算得出的正反向临界转速比解析法得到的略小,且转轴反向临界转速小于正向临界转速。改进傅里叶级数计算得出的转轴系统正反向临界转速与解析法计算得出的临界转速误差很小,且随着临界转速阶数的增大而增大,前五阶临界转速最大误差为0.004%。
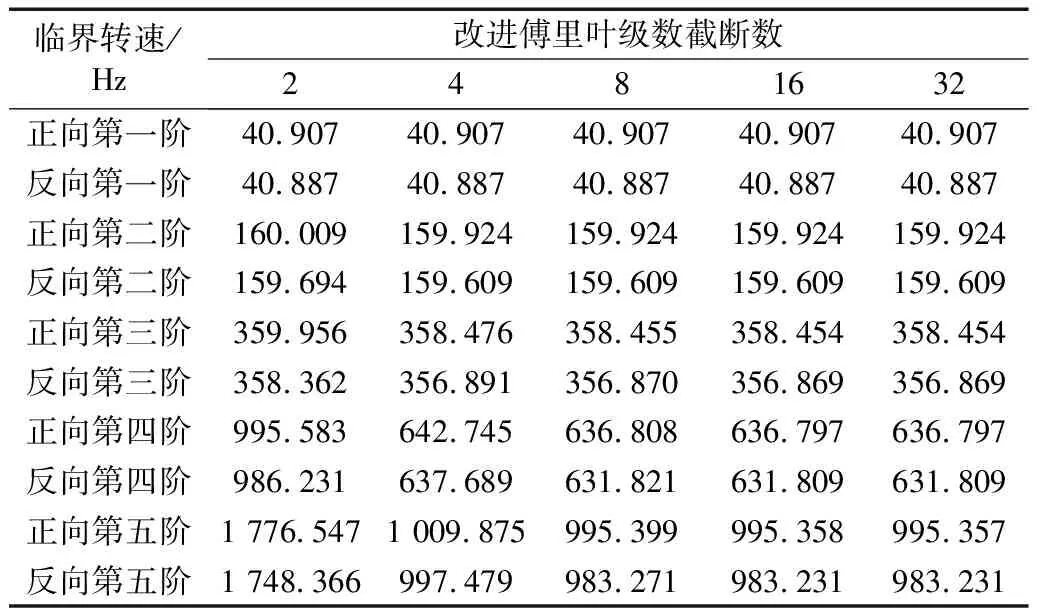
表2 不同截断数转轴的正反向临界转速
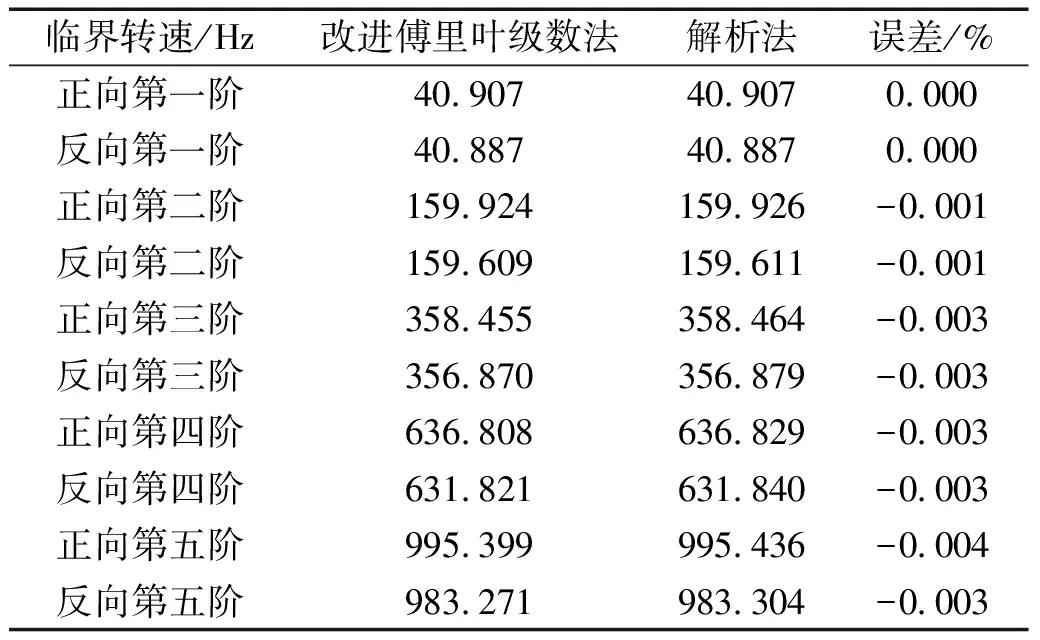
表3 正反向临界转速本文解与解析解对比
3.1.3 对比文献法及有限元法
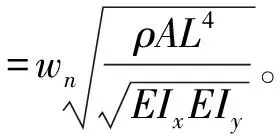
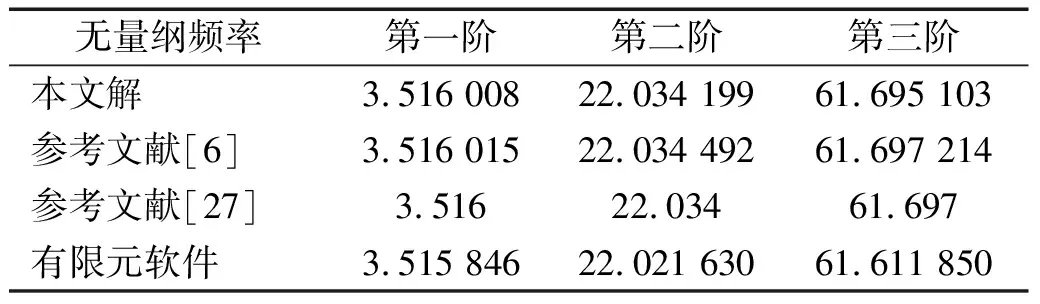
表4 本文解与参考文献、有限元软件对比
通过将本文解与参考文献解以及有限元数值解对比得到,在无量纲转速为0时,本文解的前三阶频率与参考文献解在千分位有差别,与有限元法解在百分位有差别。转轴的前三阶无量纲频率对比不同的方法均较为接近,验证了本文方法的准确性与可靠性。
通过将本文改进傅里叶级数法分别与解析法、参考文献解以及有限元法的对比得出,本文改进傅里叶级数法计算得出转轴系统正反向临界转速精确较高,且适用于转轴在不同边界条件下临界转速的计算。
3.2 复杂边界条件对转轴临界转速的影响
3.2.1 轴向载荷对转轴临界转速的影响
通过分析轴向载荷变化对转轴临界转速的影响可得,在轴向载荷为拉应力时,随着载荷在0~10 000 N的区间内不断增大,边界约束无论是简支还是固支,转轴各阶正反向临界转速均随着载荷数值的增大而增大;在轴向载荷为压应力时,随着载荷在0~-10 000 N区间内的数值不断增大,边界约束无论是简支还是固支,转轴各阶正反向临界转速均随着载荷数值的增大而减小。
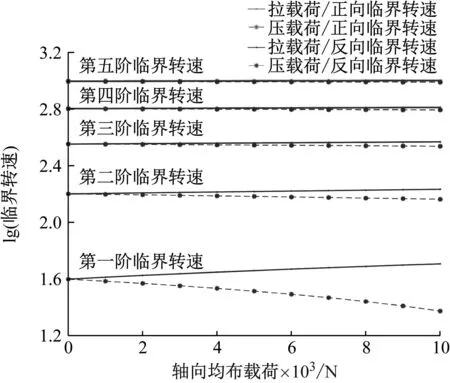
图4 两端简支支承转轴临界转速随轴向载荷的变化
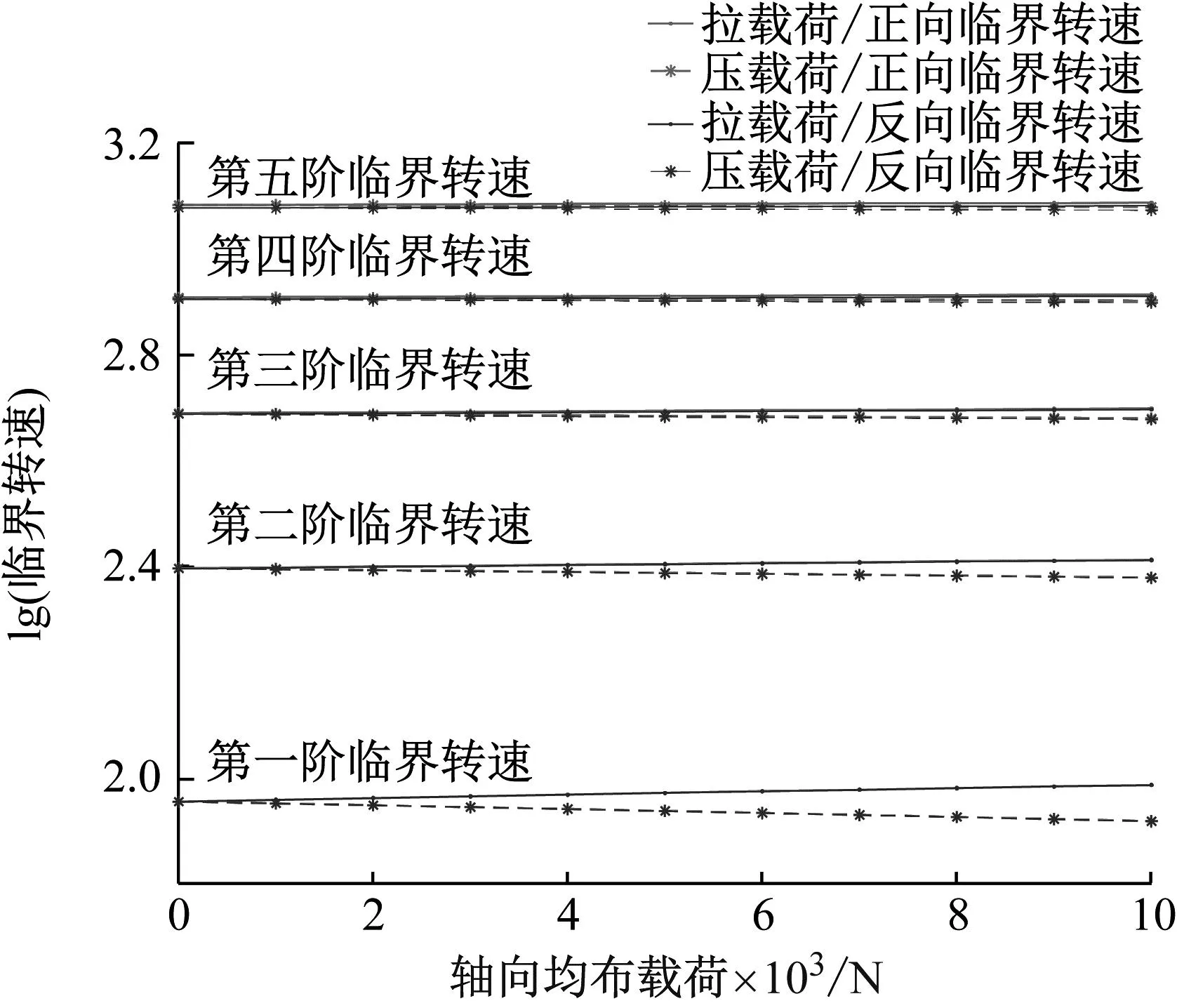
图5 两端固支支承转轴临界转速随轴向载荷的变化
3.2.2 边界约束条件对转轴临界转速的影响
本节分别探究转轴正反向临界转速随边界平动刚度和旋转刚度变化的规律。研究不同平动刚度时,转轴两端支承的旋转刚度恒为0,转轴两端支承的平动刚度由0逐渐增大为1010N/m,即转轴边界约束处于自由与简支之间;研究不同旋转刚度时,转轴两端支承的平动刚度恒为1010N/m,转轴两端支承的旋转刚度由0逐渐增大为1010N·m/rad,即转轴边界约束处于简支与固支之间。
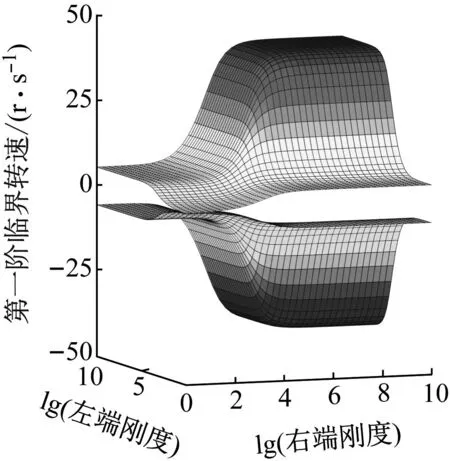
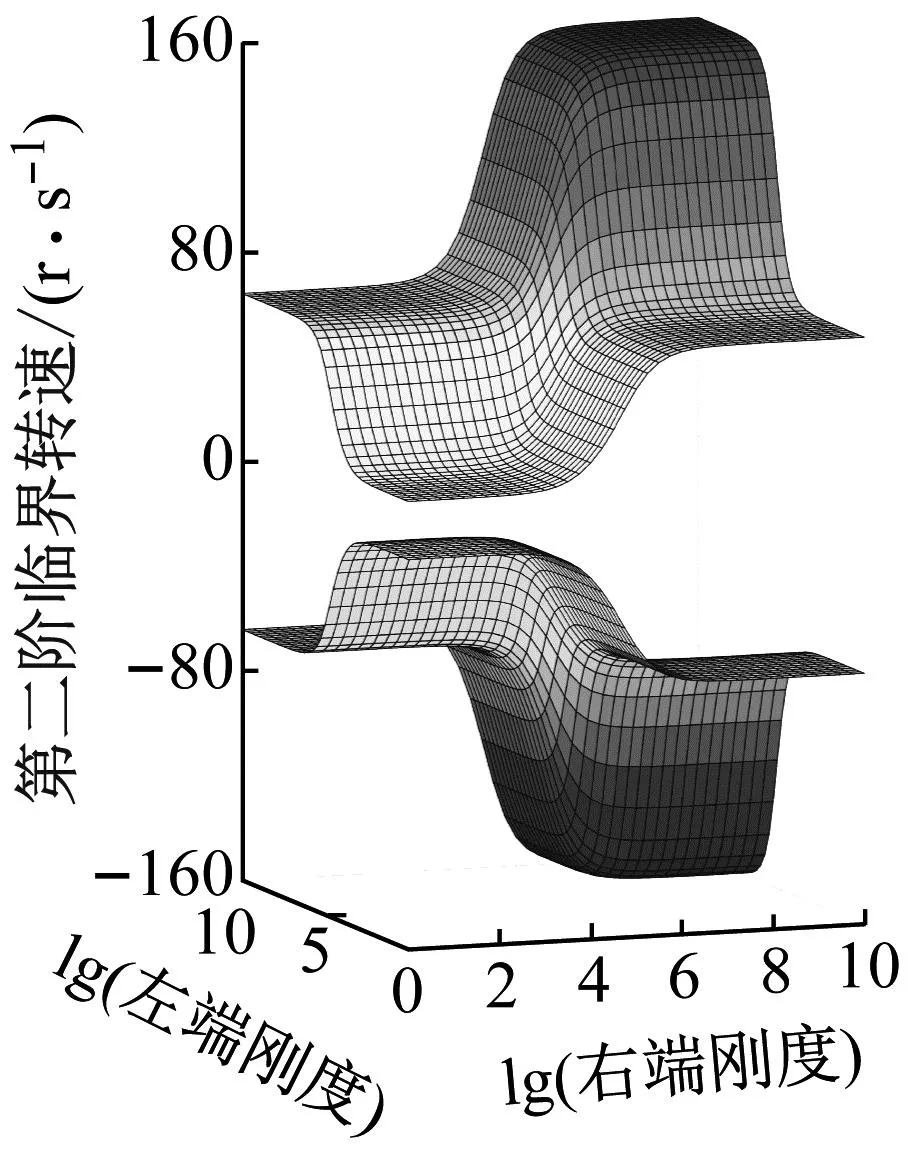
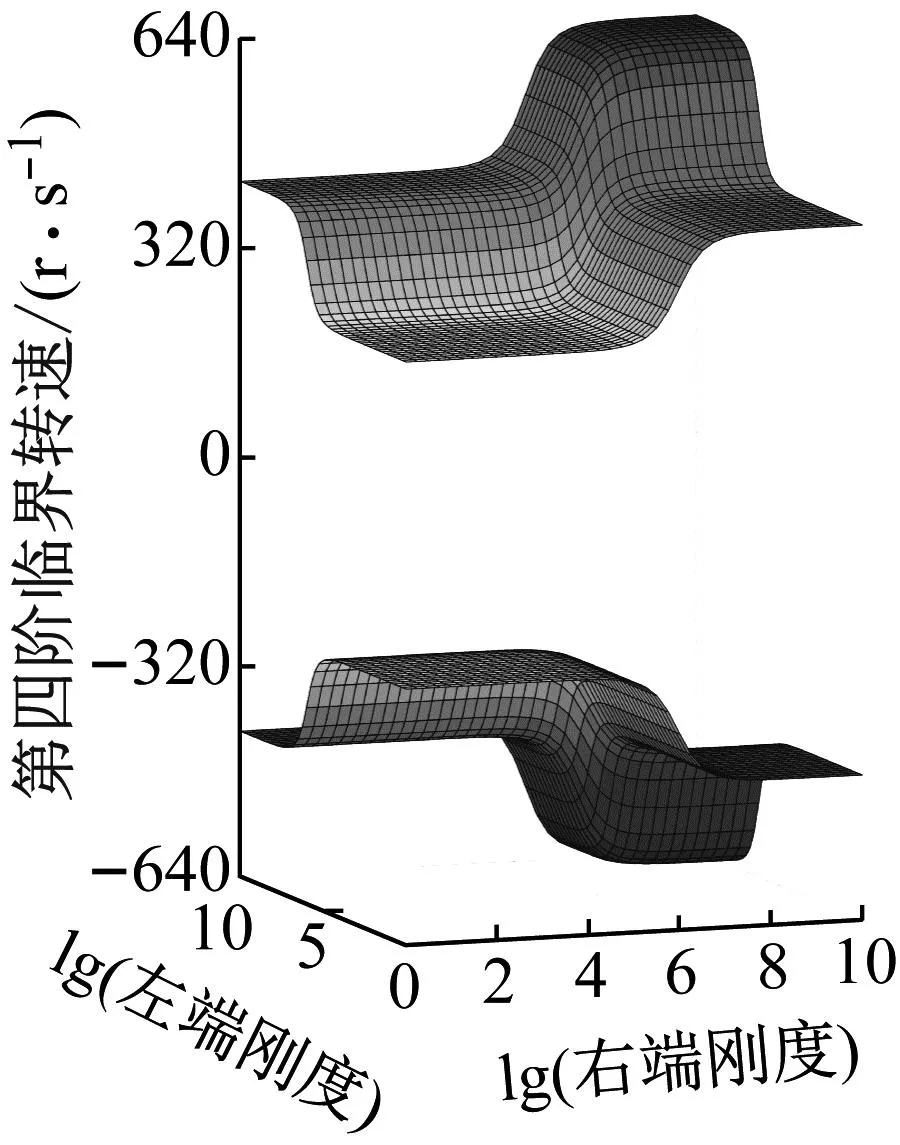
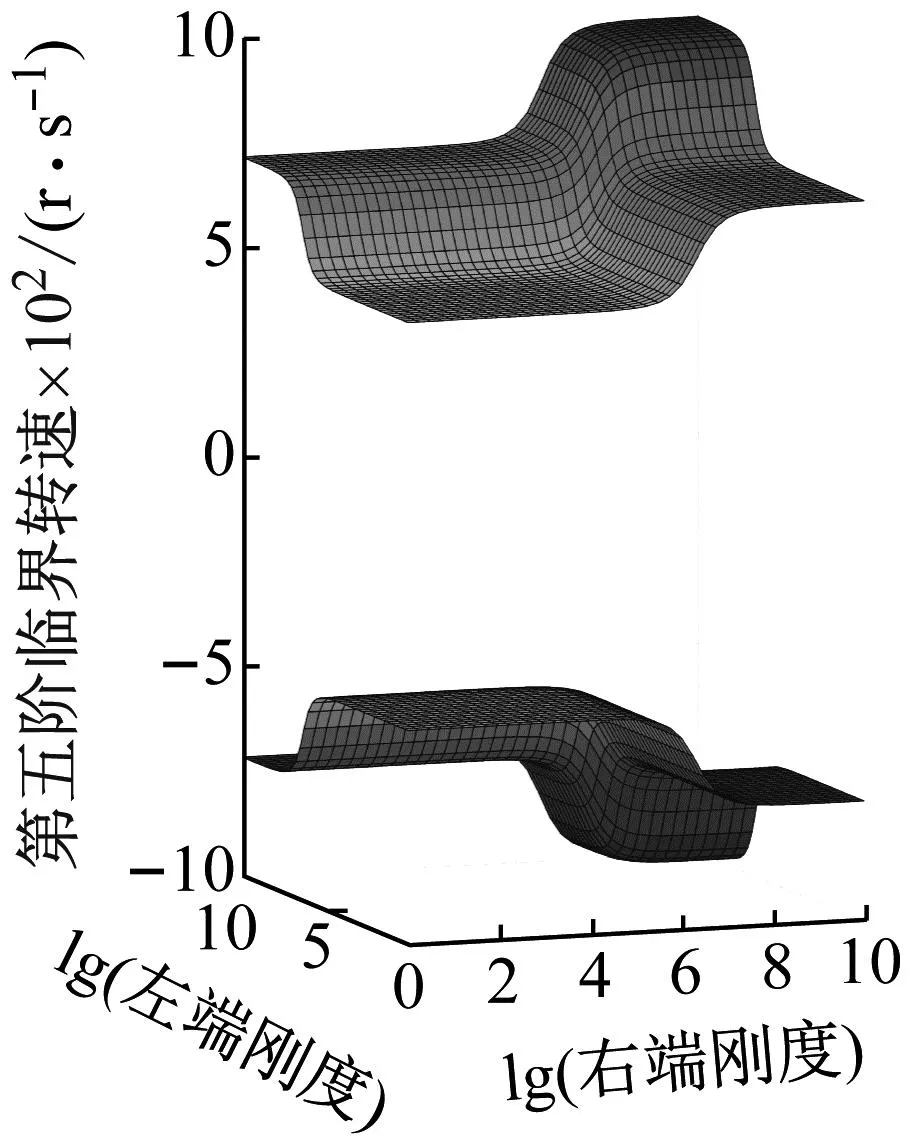
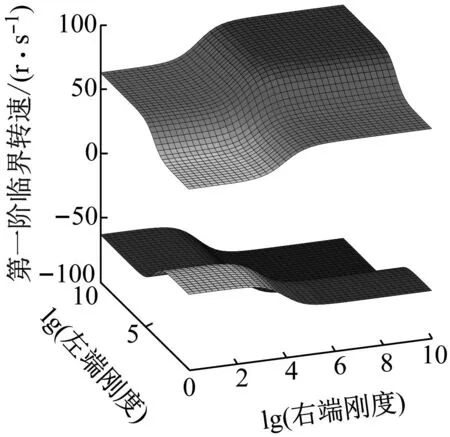
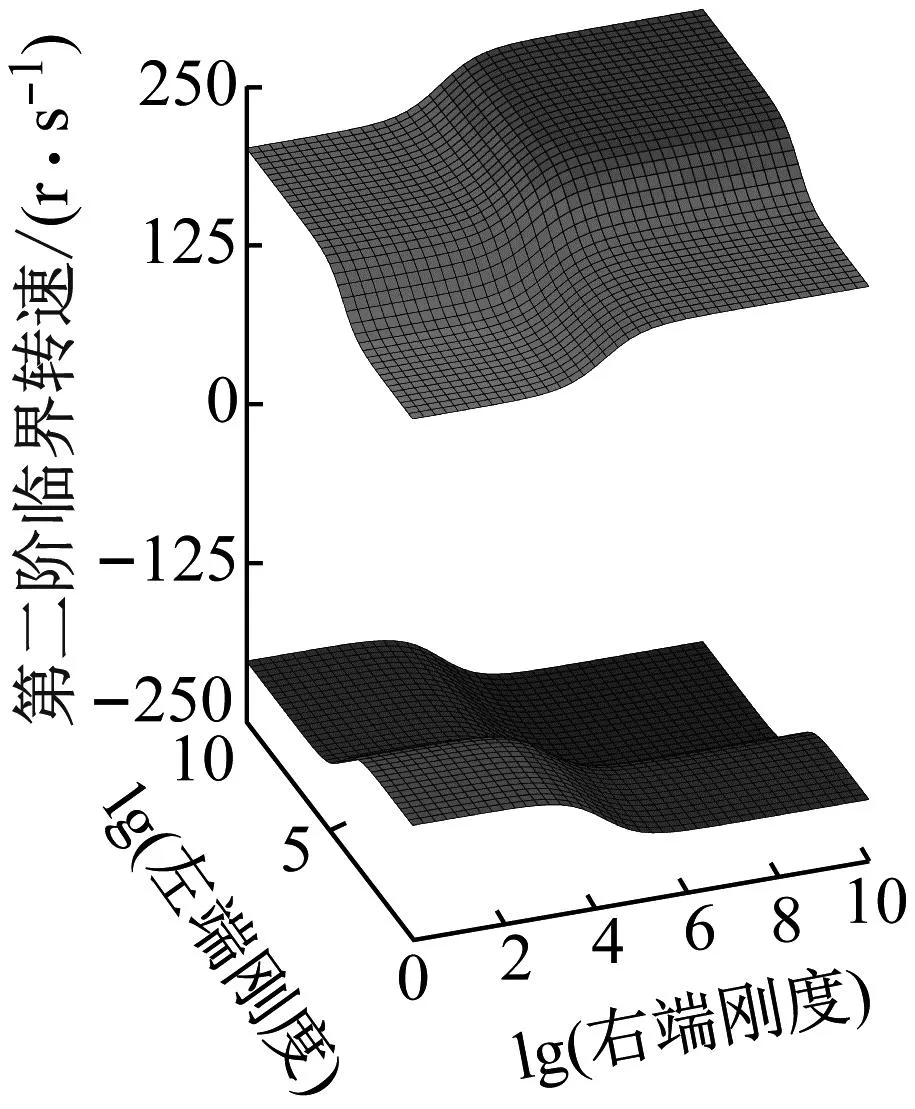
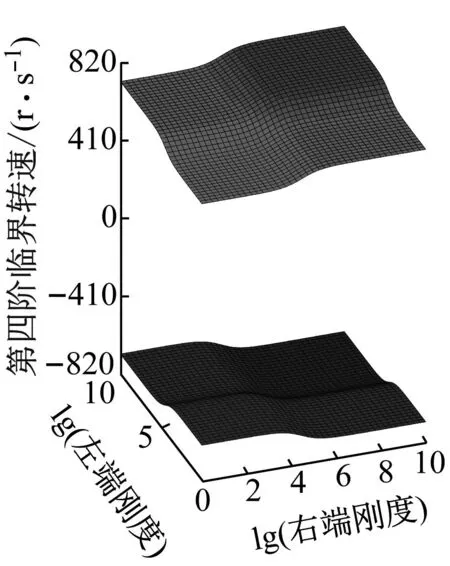
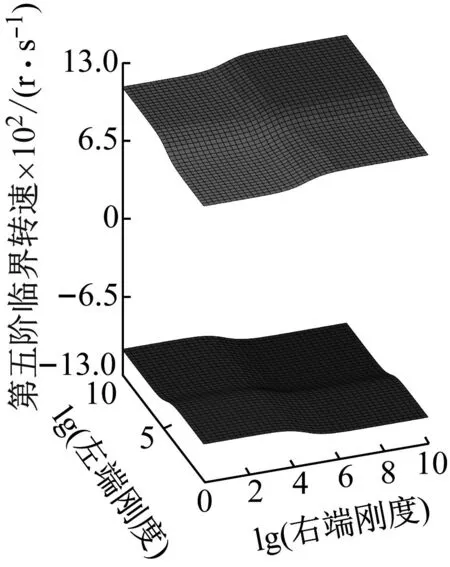
分别绘制出转轴前五阶正反向临界转速随转轴两端支承平动刚度或旋转刚度变化的曲面图,如图6、图7所示。
(a) 第一阶
(b) 第二阶

(c) 第三阶
(d) 第四阶
(e) 第五阶
在(a)~(e)五个子图中,每张子图中上半部分为转轴正向临界转速,下半部分为转轴反向临界转速。x坐标轴为转轴右端支承以10为底刚度的对数,y坐标轴为转轴左端支承以10为底刚度的对数。以第一阶正反向临界转速为例,转轴正反向临界转速均随着两端支承平动刚度或旋转刚度的不断增大而增大。在转轴两端支承平动刚度或旋转刚度较低和较高时,临界转速的增幅较小且在某些位置的增幅接近于0;平动刚度在102~106N/m范围内或旋转刚度在103~105N·m/rad范围内时,转轴正反向临界转速的增幅较大。
(a) 第一阶
(b) 第二阶

(c) 第三阶
(d) 第四阶
(e) 第五阶
3.3 不平衡集中质量对转轴横向振动的影响
在实际工程中,燃气轮机转子涡轮、柴油机输出轴、船舶艉轴等转子转轴机械,由于生产制造中存在工艺缺陷、安装误差以及工作环境恶劣等因素,转轴自身可能出现一处或多处集中质量。这些不平衡集中质量的质量过大,或转轴转速较高时,集中质量对转轴横向振动的影响不可忽略。不平衡集中质量作为结构质量将影响转轴的正反向临界转速,不平衡集中质量绕轴心转动作为激励将影响转轴的幅频特性。同时转轴在具有不平衡集中质量的前提下,在不同边界条件(轴向载荷、边界约束)将表现出不同的幅频特性。
3.3.1 不平衡集中质量的大小对转轴涡动频率的影响
本节研究不平衡集中质量作用于转轴时,不同边界约束条件下转轴正反向涡动频率随集中质量大小改变的变化情况。
图8为两端简支支承下转轴涡动频率图。图9为两端固支支承下转轴涡动频率图。图8和图9中分别绘制了集中质量m0为0、1 kg、2 kg时,转轴前五阶正反向涡动频率随转轴转速的变化,图中的黑线为斜率等于一的直线,黑线与各个涡动频率线的交点为转轴的临界转速,图8、图9为转轴临界转速图,即坎贝尔图(Campbell diagram)。转轴在临界转速附近运行工作时,转轴横向振动的振幅较大,其详细幅频规律将在后续小节讨论。
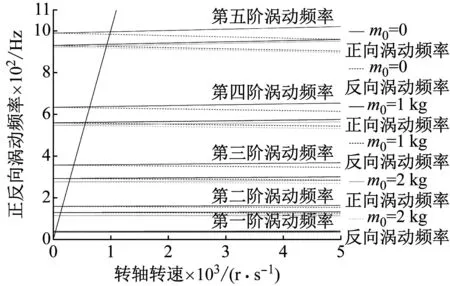
图8 两端简支支承不同集中质量转轴临界转速图
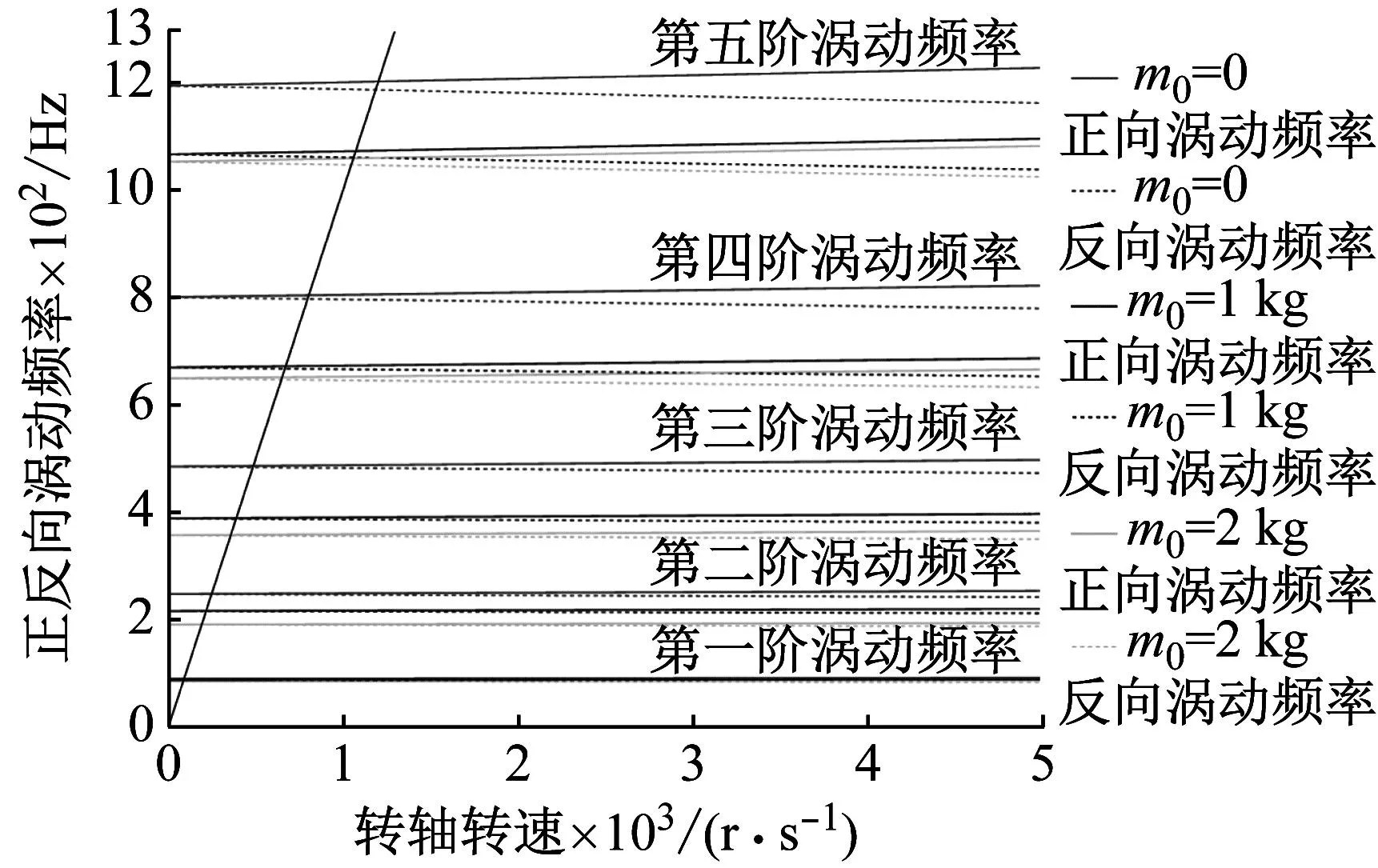
图9 两端固支支承不同集中质量转轴临界转速图
分析图8、图9可以得出,随着集中质量的逐渐增大,转轴各阶正反向涡动频率以及各阶正反向临界转速均逐渐减小。集中质量对转轴高阶正反向涡动频率和高阶正反向临界转速的影响大于对低阶的影响。
3.3.2 边界约束条件对转轴幅频特性曲线的影响
不平衡集中质量作为外激励,其激励频率等于转轴转速,其激励幅值大小与集中质量、偏心距、转轴转速平方均成正相关。本节所用参数如下,不平衡集中质量的质量为m0=1 kg,不平衡集中质量的偏心距为r=0.01 m,不平衡集中质量的轴向作用位置为距离转轴左端zm=0.1 m处,转轴横向振动响应振幅提取位置为转轴左端点。
图10为转轴左端点横向振动幅频特性随转轴两端平动刚度变化的曲线,坐标横轴为转轴转速,坐标纵轴为以10为底转轴振幅的对数。转轴两端支承的平动刚度从2×109N/m增加至1010N/m,转轴两端旋转刚度为0,即转轴两端为简支约束。通过分析可得,在保持激励不变的情况下,转轴左端点响应振幅随着转轴两端平动刚度的增大而减小;转轴左端点横向振动频谱曲线的前五阶共振峰与反共振峰峰值均随着转轴两端平动刚度的增大而减小;转轴左端点横向振动频谱曲线的前五阶共振峰与反共振峰对应的峰值频率随着转轴两端平动刚度的变化几乎没有变化。
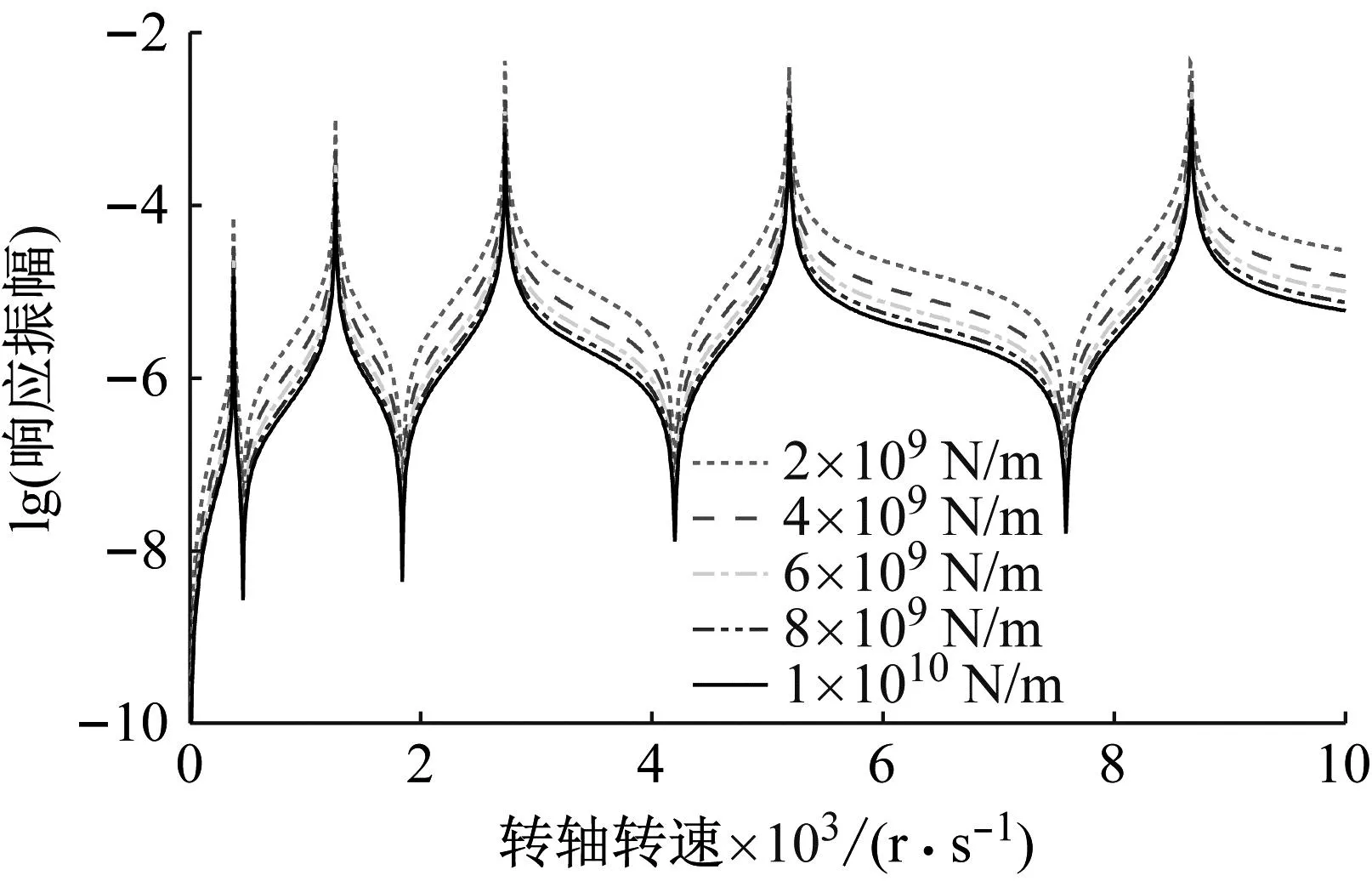
图10 转轴幅频特性曲线随两端平动刚度的变化
图11为转轴左端点横向振动幅频特性随转轴两端旋转刚度变化的曲线,坐标横轴为转轴转速,坐标纵轴为以10为底转轴振幅的对数。转轴两端支承的旋转刚度从102N·m/rad增加至1010N·m/rad,转轴两端平动刚度为1010N/m,即转轴两端约束由简支约束逐渐过渡为固定约束。通过分析可得,转轴左端点响应振幅随着转轴两端旋转刚度的增大而增大;转轴左端点横向振动频谱曲线的前五阶共振峰随着转轴两端旋转刚度的增大而增大;转轴左端点横向振动频谱曲线的前五阶共振峰与反共振峰对应的频率随着转轴两端旋转刚度的增大而增大。
3.3.3 集中质量作用位置对转轴幅频特性的影响
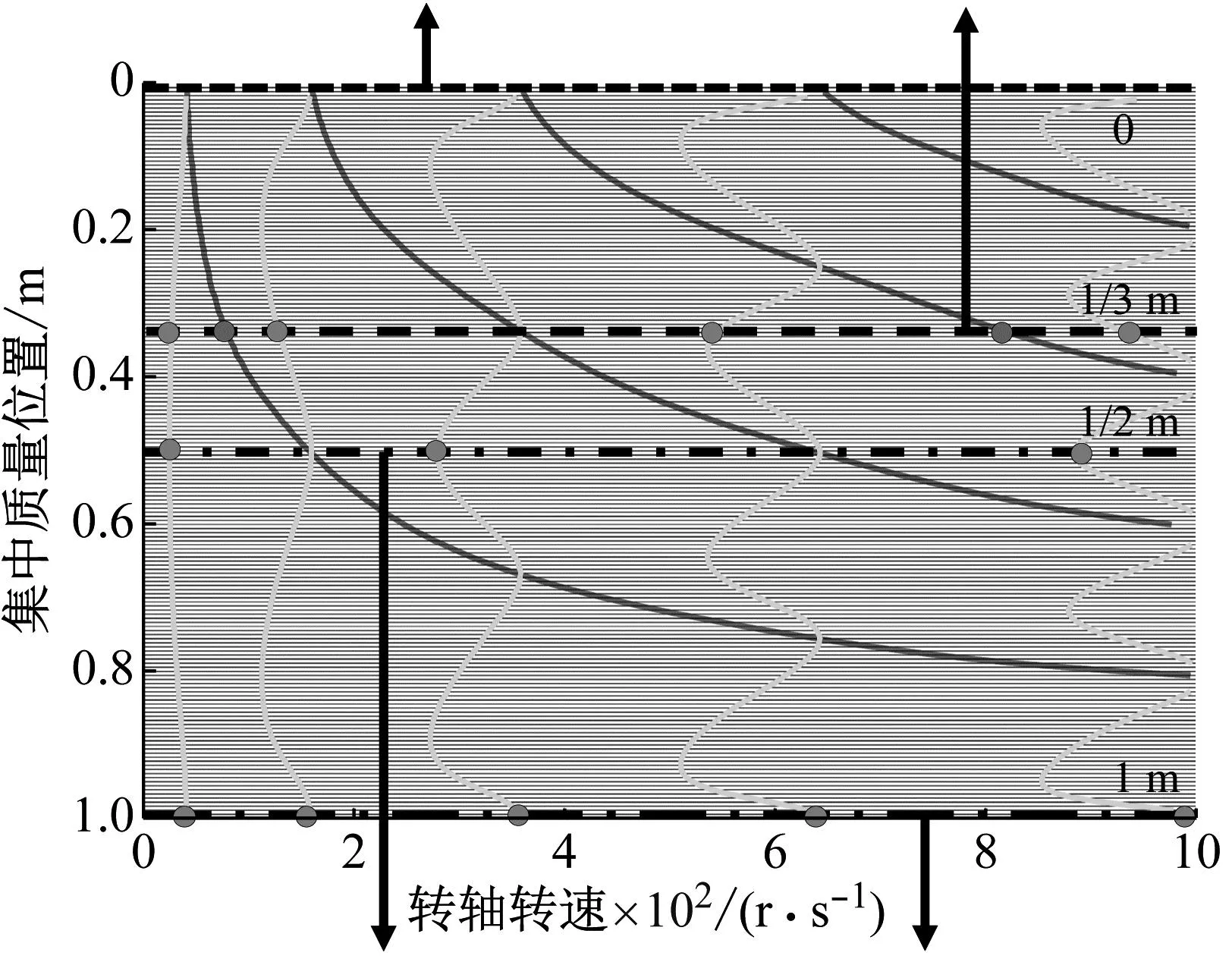
不平衡集中质量作用在转轴的轴向位置会影响转轴幅频特性,本节将研究集中质量在转轴各个轴向位置处的幅频特性曲线,将这些曲线组绘制于同一张瀑布图中并探求其中规律。
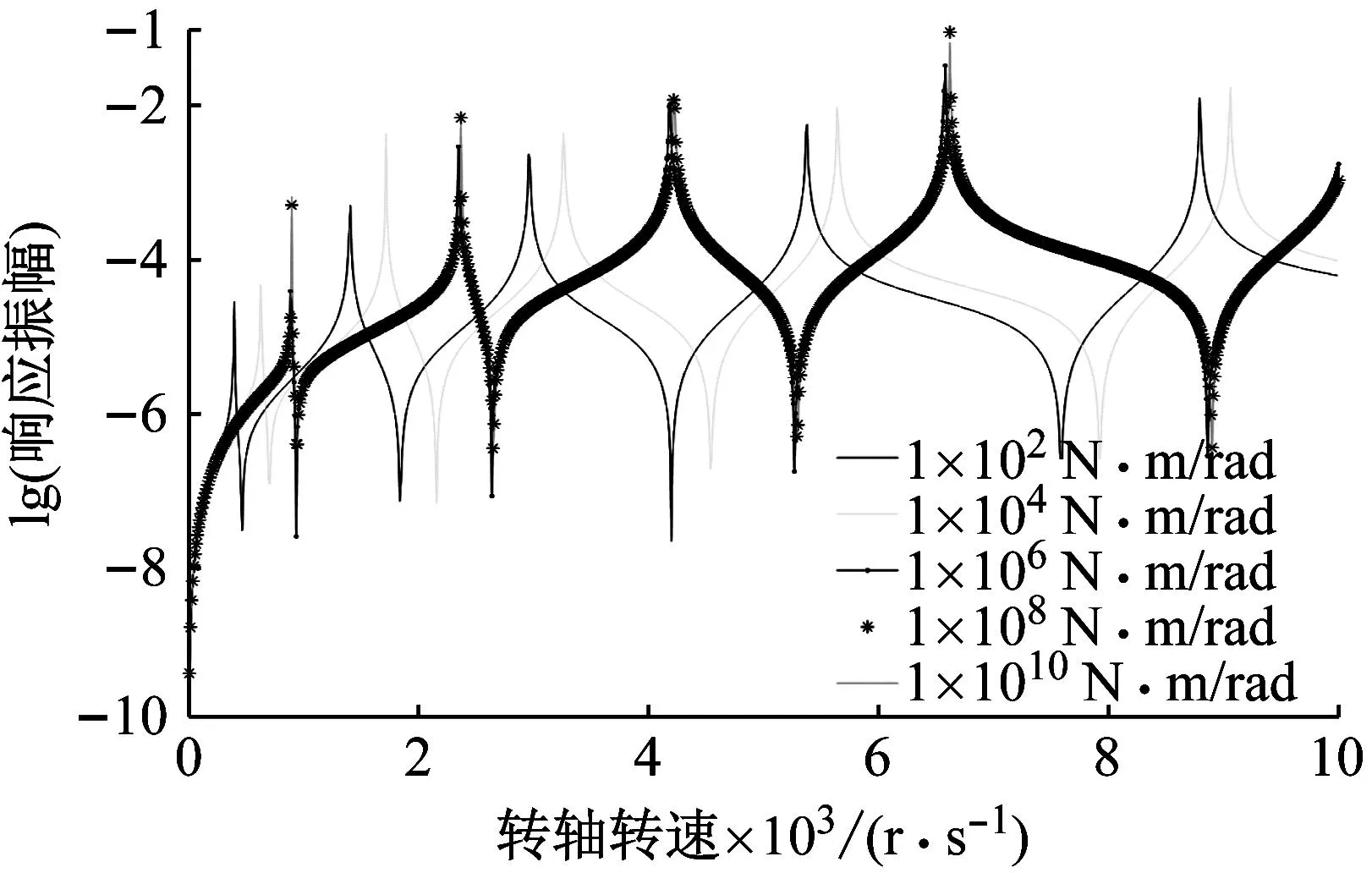
图11 转轴幅频特性曲线随两端旋转刚度的变化
改变不平衡集中质量作用在转轴的轴向位置,同时保持不平衡集中质量的质量、偏心距不变,保持转轴两端恒为简支支承,将转轴转速从0均匀提高至1 000 r/s(Hz),绘制出多组转轴幅频特性曲线如图12所示。在图12中,不平衡集中质量的位置从距离转轴左端0处逐渐增大至1 m,即从转轴左端逐渐平移至右端,转轴幅频特性曲线的提取位置为转轴左端。所绘制瀑布图的纵坐标为转轴左端横向振动位移幅值以10为底的对数值。
以图12为基础,将每条转轴横向振动幅频特性曲线的每阶共振峰用绿线依次连接,将每条转轴横向振动幅频特性曲线的每阶反共振峰用红线依次连接,得到图13中的共振峰线和反共振峰线。由于本文只探究转轴的前五阶临界转速,所以图13中的转轴转速只截止绘制到了1 000 Hz,由于第五阶反共振峰对应的转速大于1 000 Hz,因此图中在该频率范围内只包含转轴幅频特性曲线前五组共振峰线和前四组反共振峰线。
为了便于分析共振峰线与反共振峰线的线形特征,绘制出图13的俯视图(图14)。分析图14可得,转轴幅频特性曲线的共振峰线和反共振峰线成对出现。随着集中质量轴向位置的偏移,前五组共振峰线对应的转轴转速分别围绕着转轴前五阶临界转速左右波动,且各组共振峰随集中质量位置波动的周期数与该共振峰线对应的阶数相同。所以从另一个角度来讲,本文对于转轴幅频特性曲线的处理方法可近似得到转轴模态振型及临界转速。
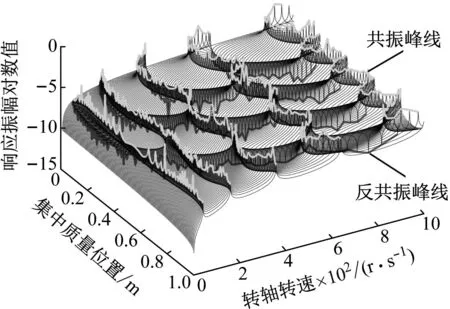
图13 共振峰线与反共振峰线
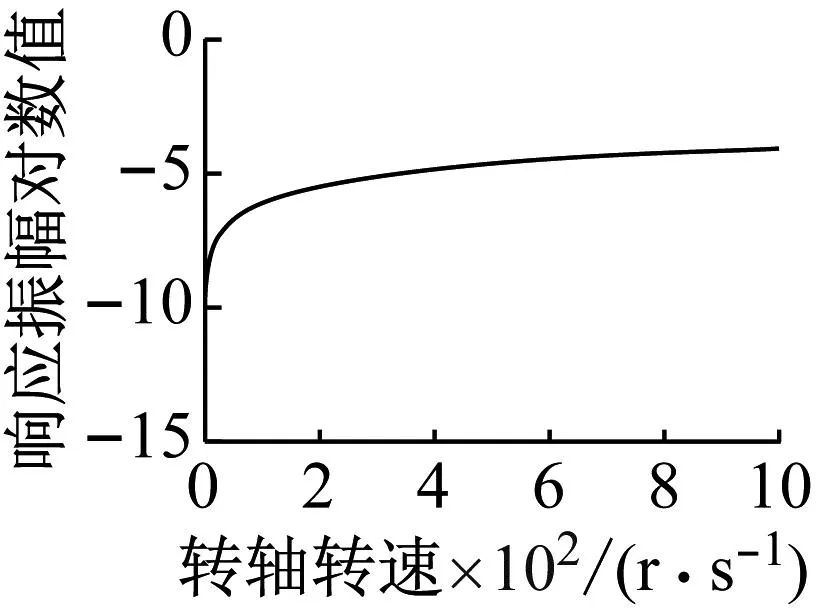
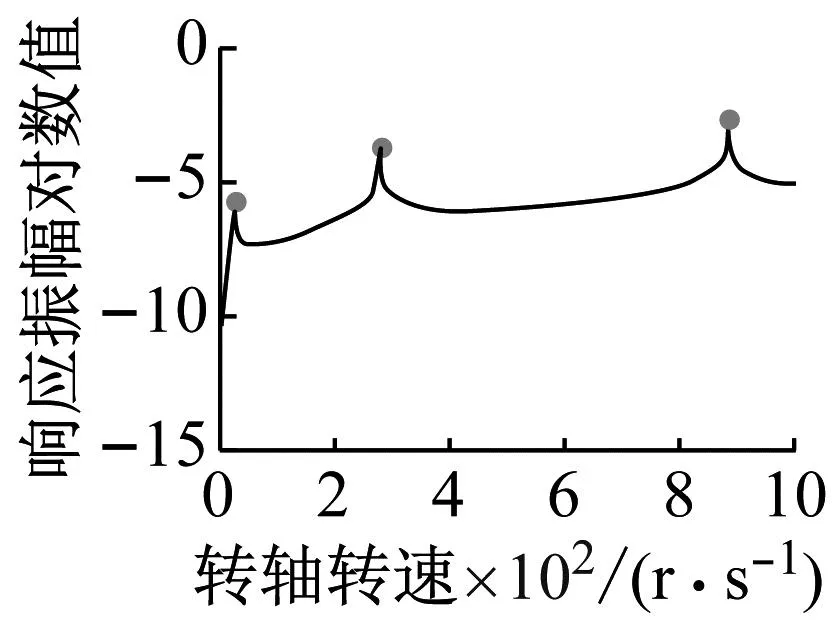
(a) 0处

(b) 1/3 m处
(c) 1/2 m处
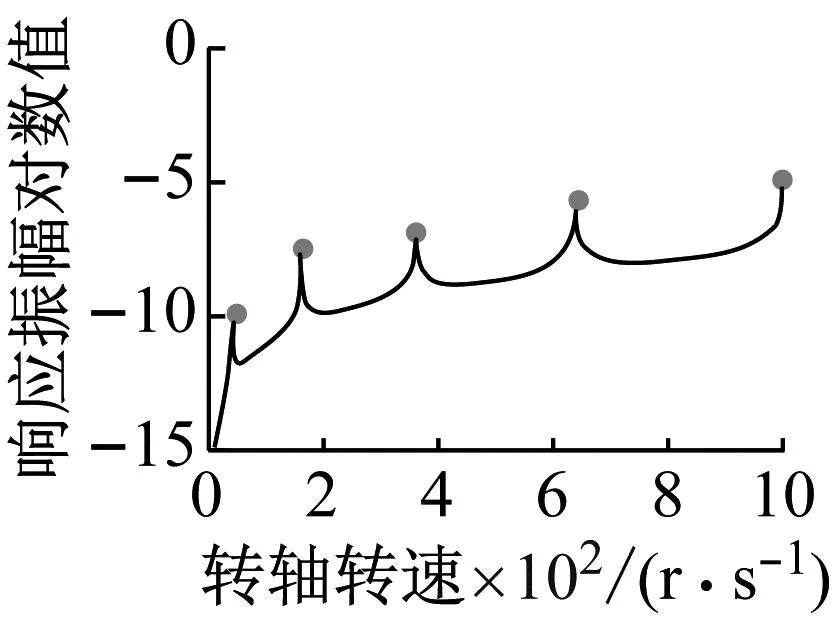
(d) 1 m处
随着集中质量轴向位置的偏移,前四阶反共振峰线对应的转轴转速不断增大,且反共振峰线的起始点与共振峰线的起始点相同。反共振峰线随着集中质量位置的增大而偏移,导致某阶反共振峰线与次阶及其后阶共振峰线相交,相交位置处的转轴幅频特性曲线在对应转速位置处无共振峰和反共振峰。
上述分析方法从一个新角度阐释了:不平衡集中质量在转轴某处轴向位置激起的转轴幅频特性曲线不存在某阶共振峰或反共振峰。转轴转速在0~1 000 Hz的区间内,不平衡集中质量作用于转轴左端时(图14(a)所示),由于转轴幅频特性曲线的每组共振峰与反共振峰重合,所以该幅频特性曲线为光滑曲线,不存在共振峰与反共振峰;不平衡集中质量作用于转轴1/3位置处时(图14(b)所示),由于转轴幅频特性曲线的第三阶共振峰与第二阶反共振峰重合,所以该幅频特性曲线第二阶共振峰与第四共振峰之间为光滑曲线;不平衡集中质量作用于转轴轴向中点位置时(图14(c)所示),由于转轴幅频特性曲线的第二阶共振峰与第一阶反共振峰重合,第四阶共振峰与第二阶反共振峰重合,所以该幅频特性曲线只有第一阶、第三阶和第五阶共振峰,且不存在反共振峰;不平衡集中质量作用于转轴轴向4/5至右端范围内时(图14(d)所示),由于转轴幅频特性曲的共振峰与反共振峰无交点且无反共振峰线的存在,该幅频特性曲线存在前五阶共振峰且不存在反共振峰。
4 结 论
为了研究含不平衡质量以及弹性边界条件对转轴横向振动的影响,本文建立了以改进傅里叶级数为假设振型的转轴横向振动模型。运用第二类拉格朗日方程推导出转轴横向振动运动学方程组,对运动方程组进行处理、求解得到不同因素对转轴横向振动的影响,并对这些结果进行总结如下:
(1) 以改进傅里叶级数为假设振型计算得出的转轴横向振动正反向临界转速的精度以及收敛性较好,与解析法、参考文献和有限元法对比求解的误差均较小。
(2) 转轴正反向临界转速随着轴向拉应力载荷的增大而增大,随着轴向压应力载荷的增大而减小;转轴正反向临界转速随着两端支承平动刚度和旋转刚度的增大而增大,刚度在较小和较大的范围内变化时,转轴正反向临界转速增幅较小;刚度在适中的范围内变化时,转轴正反向临界转速增幅较大。
(3) 随着不平衡集中质量逐渐增大,转轴各阶正反向涡动频率以及各阶正反向临界转速均逐渐减小,且集中质量对转轴高阶正反向涡动频率和高阶正反向临界转速的影响大于对低阶的影响;在不平衡集中质量的激励下,转轴横向振动幅值随着转轴两端支承平动刚度的增大而降低。
(4) 转轴幅频特性曲线的共振峰线与反共振峰线交错分布,其交点位置对应的转轴幅频特性曲线为光滑段;本文以一个新角度阐释了不平衡集中质量如何通过轴向位置影响转轴幅频特性曲线共振峰与反共振峰的峰值、数量与位置。

