管束结构的阻尼控制型流弹失稳特性研究

冯志鹏, 臧峰刚, 刘 帅, 黄 旋, 齐欢欢

(中国核动力研究设计院 核反应堆系统设计技术重点实验室,成都 610213)

在核工程领域,流致振动仍然是影响蒸汽发生器性能的主要限制因素,流弹失稳(流体弹性不稳定性)是最具破坏性的流致振动机理[1]。尤其是2012年美国圣奥诺弗雷核电站(SONGS)因流致振动而导致蒸汽发生器失效后,人们又开始重点关注管束的流弹失稳。

流弹失稳(fluid-elastic instability, FEI)是由两种流体-结构相互作用机制引起的：①与相邻管振动的流体耦合有关,称为流体刚度控制机制;②与管速度相关的流体力分量相关,称为流体阻尼控制机制。已有研究表明[2],阻尼机制在较低质量阻尼参数下占主导地位,刚度机制在较高质量阻尼参数下占主导地位。压水堆中的蒸汽发生器管束属于低质量阻尼参数范围,容易发生流体阻尼控制型流弹失稳。

长期以来,管束流弹失稳研究主要依赖于试验,提出的许多半经验模型忽略了湍流强度、雷诺数等因素的影响,但在实际工程中,管束中的流动通常是黏性和湍流的,在没有经验数据的情况下对流动进行详细描述的最佳途径是采用计算流体力学(computational fluid dynamics, CFD),如De Pedro等[3]研究了阻尼控制型流弹失稳的数值模型,Khalifa等[4]利用ANSYS-CFX建立了管束的CFD模型,预测了流弹失稳的稳定性,冯志鹏等[5]通过理论建模和CFD相结合的方式,发展了流弹失稳行为的数值预测方法。

尽管自SONGS事故以来,对流弹失稳的分析方法与建模工具等方面都进行了改进,如考虑到了之前忽略的一些因素、采用更复杂的公式来解释两相流效应和流向不稳定的影响,但导致这种不稳定现象的根本因素尚未确定,仍有待于进一步研究。同时,在通过CFD研究流弹失稳时,尚缺乏有效的确定主导激励机理的手段和判定管束流弹系统稳定性的指标。

本文针对压水堆蒸汽发生器中容易发生的阻尼控制型流弹失稳,基于开源CFD工具OpenFOAM建立流固耦合数值模型,从宏观响应特性、能量输入与耗散、升力与位移间的相关性、升力的频谱特性等层面研究流弹失稳行为,提出更好反映管束流弹系统稳定性和确定主导激励机理的分析方法。

1 数值模型

1.1 流场模型

平行三角形管束及其计算域,如图1所示。节径比Pr=1.5。计算域包含了21行7列管,其中深色的管可在横向自由振动(称为运动管),上下两侧为半管。进口位于第一排管子的15D处(D为管子外径),已有研究表明该入口长度是合适的。

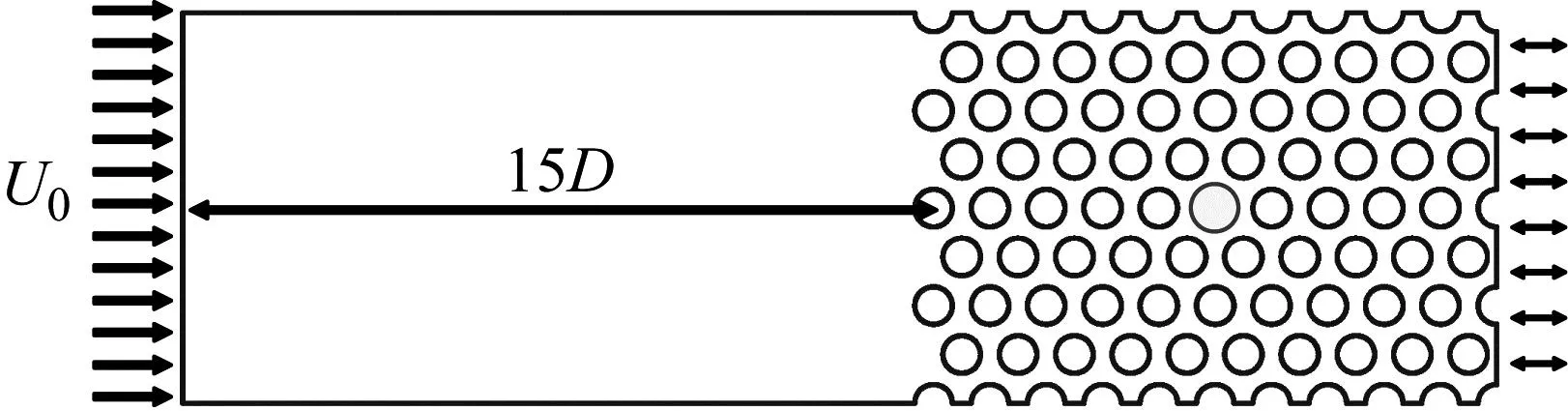
图1 计算域

湍流模拟采用两方程的剪切应力输运湍流模型(k-ωSST模型,以下简称SST模型),其在管束的流动预测中与试验吻合较好[6]。管壁面附近采用边界层,使y+≤1以保证黏性亚表层被合理求解。边界层数量为15层,并使用1.01的扩展系数从边界层单元过渡到四面体单元,网格细节如图2所示。

入口设置为均匀流动,入口湍流强度取为1%;出口设为inletOutlet条件,OpenFOAM中inletOutlet边界条件允许流体流出或流入区域,因此流体不会被迫流向出口方向;计算域沿z向的两个端面赋给empty边界条件。除了第11行中心的管为运动壁面外,流场上下侧和其它管表面为固定无滑移壁面。根据平均间隙流速,雷诺数范围为Re=2×103～4×104。

图2 网格细节

1.2 运动管的模拟

将运动管视为单自由度系统,运动方程为

(1)

1.3 离散求解

流场模拟基于开源CFD工具OpenFOAM。本文所用的离散化方案和求解器误差的详细信息,如表1所示。时间导数为隐式一阶Euler格式、对流项为线性迎风格式、扩散项为非正交修正的中心差分格式;动量方程的求解采用几何代数多重网格求解器并配合Gauss-Seidel型平滑器;其它量的求解采用光滑求解器并配合symGaussSeidel型平滑器;动网格求解器为dynamicMotionSolverFvMesh,运动边界求解器为sixDoFRigidBodyMotion。

在瞬态求解过程中自动调整时间步长,保障最大局部Courant数保持在预设极限以下,在目前的模拟中,Courant数被限制在Co<0.8。非结构三维网格上的Courant数计算如下

(2)

式中,Φf=Af(uf·nf)是垂直于f面的速度通量,f面是体积为V的单元的面Af。

每个模拟分为两个步骤：采用稳态计算求解流场,此时所有的管子保持静止;以稳态结果作为初始条件,进行具有管子运动的瞬态模拟。

2 模型验证

为验证本文建立的数值模型,首先开展网格收敛研究,然后将预测的临界流速与已有试验数据对比,验证本文建立的数值模型。

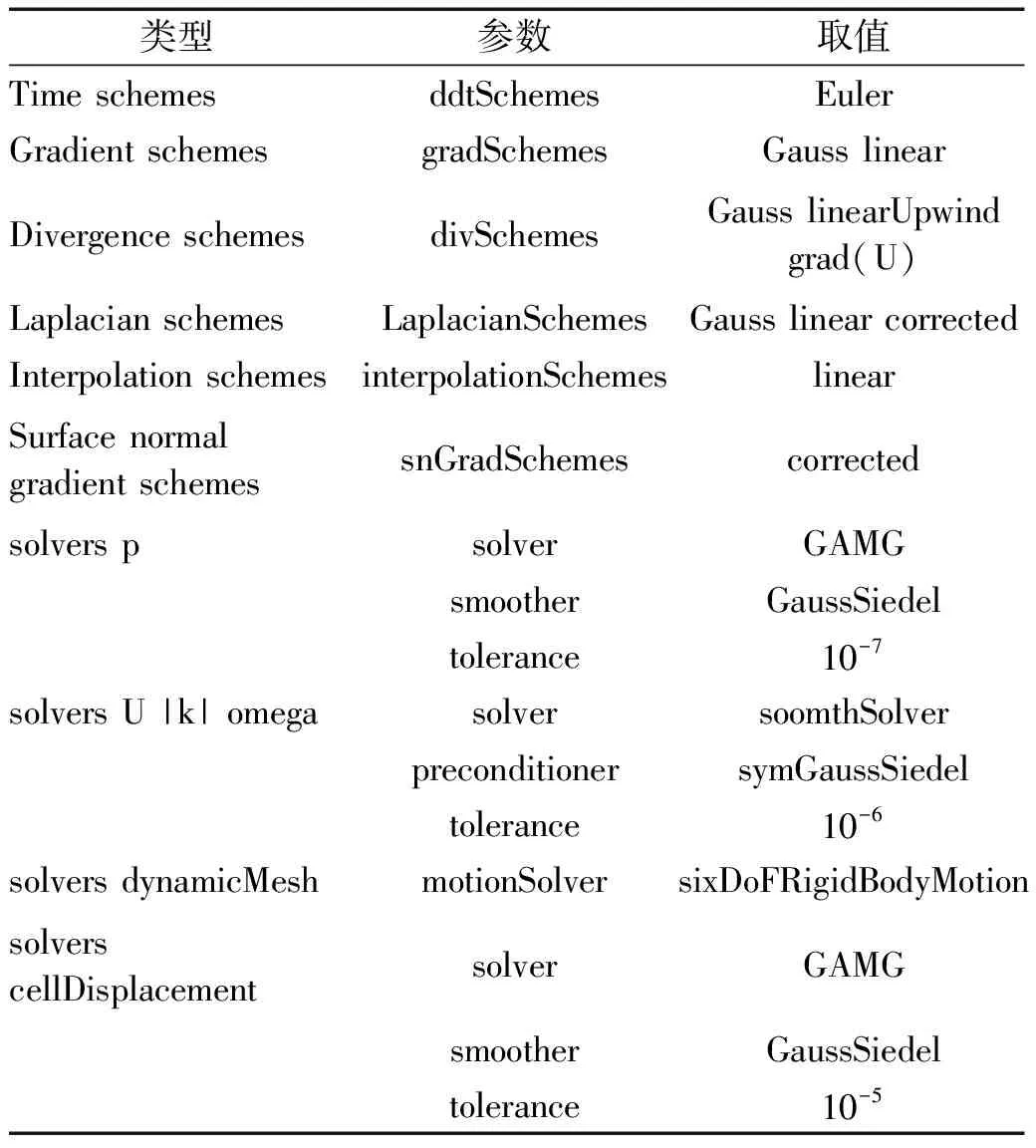
表1 离散格式和求解器

网格收敛是CFD分析的一个基本步骤。本文在静止绕流、强迫运动两个维度上进行网格无关性分析,在建立管子周围的边界层网格时,采取了两种方式：

方式一：仅在运动管及其周围的7根管子(称为Cluster)周围建立边界层,即mesh1～mesh6,如图3所示。

方式二：在所有管子周围建立边界层,即mesh21～mesh25。

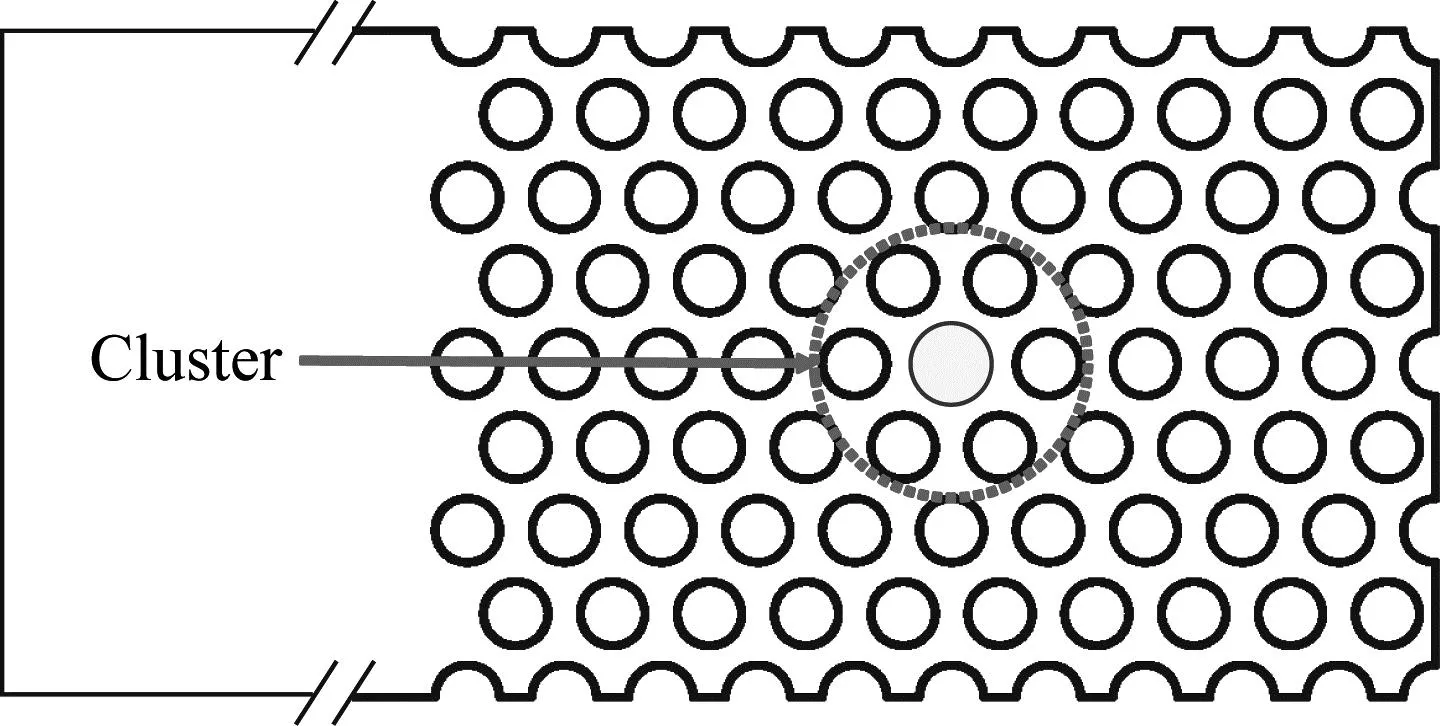
图3 仅Cluster管带有边界层的情况

网格情况如表2所示。其中size表示每个管周向网格的大小,NTotal表示网格单元数。

定义升力系数和阻力系数分别为

(3)

式中：Fl和Fd分别为作用在管子上的升力和阻力;ρ为流体密度;U0为入口流速;Ax和Ay分别为管在阻力方向和升力方向的投影面积。

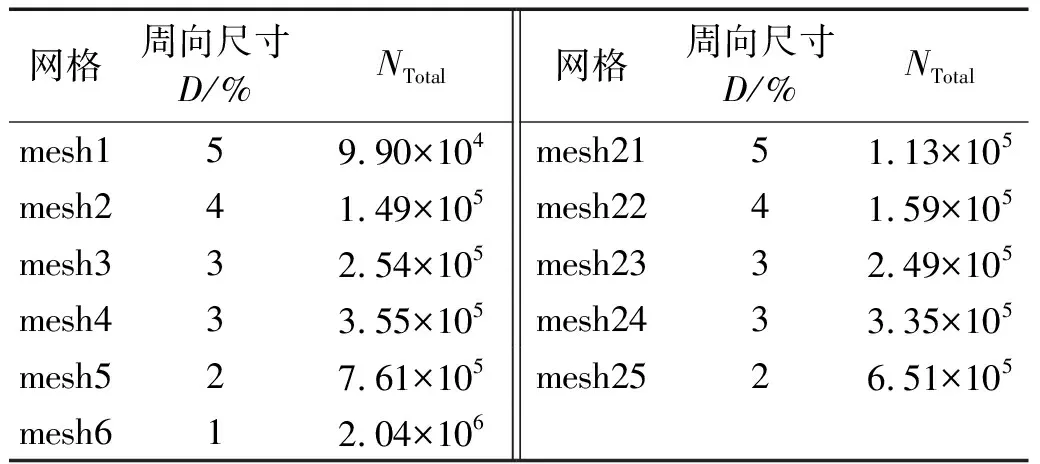
表2 网格情况

2.1 静止绕流下的网格验证

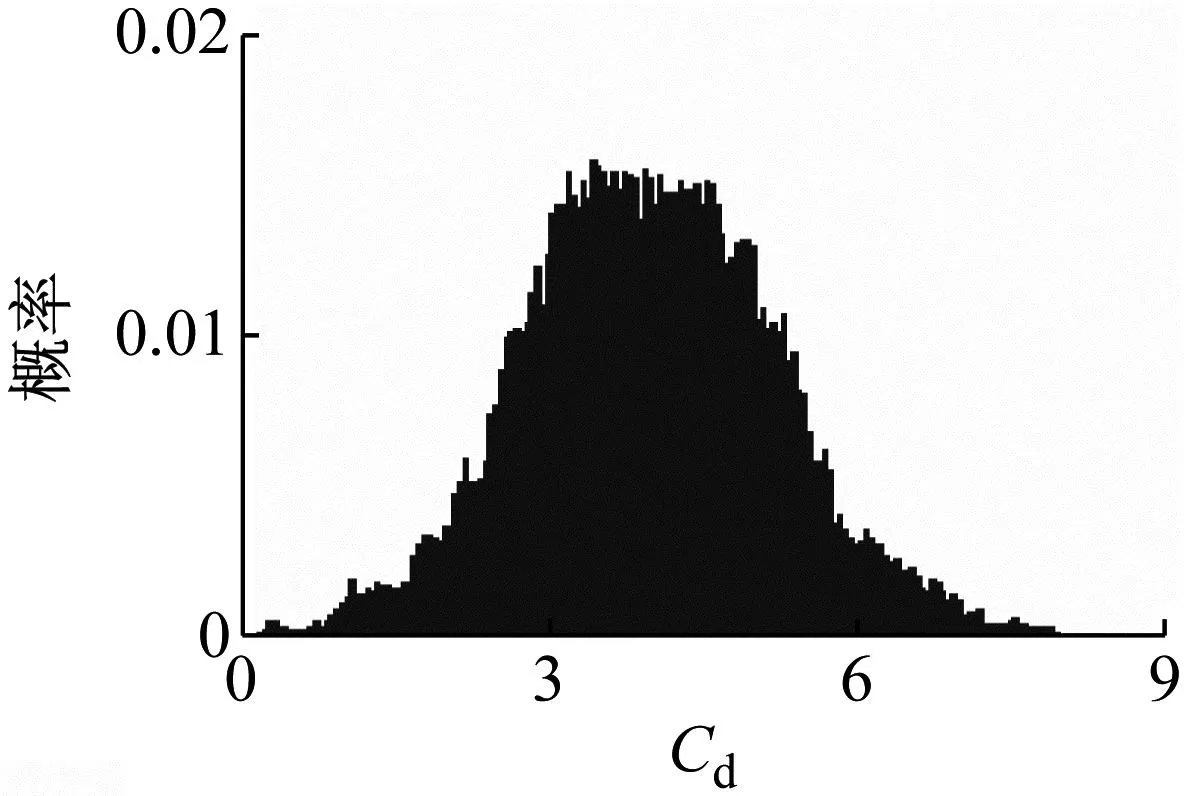
首先基于静止绕流进行网格敏感性研究,典型的升力系数、阻力系数的时程,如图4所示。实际计算得到的y+,如图5所示。由图5可知,计算得到的最大y+<1,满足SST模型对网格的要求。流体力的统计分布,如图6所示。与Mahon[7]得出的规律一致,即升力系数呈双峰分布、阻力系数呈单峰分布。

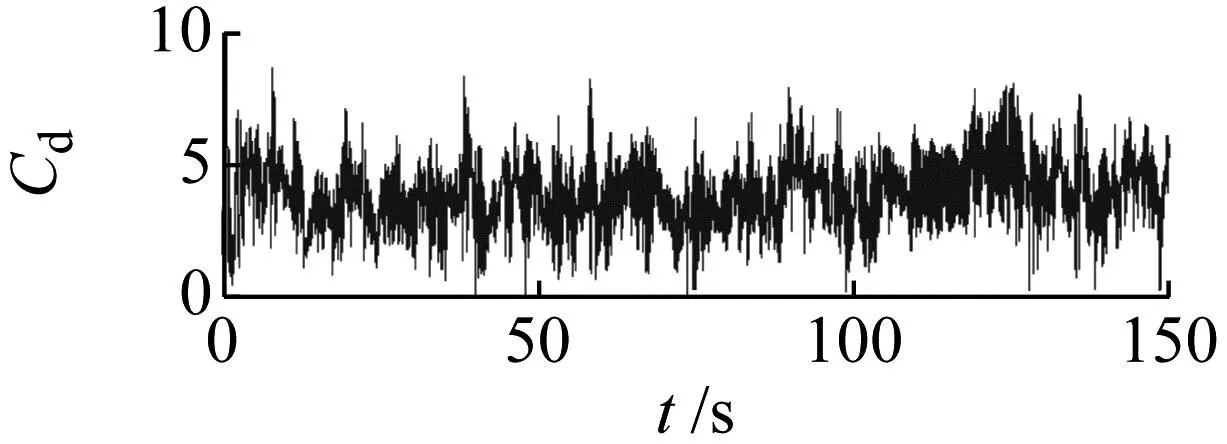
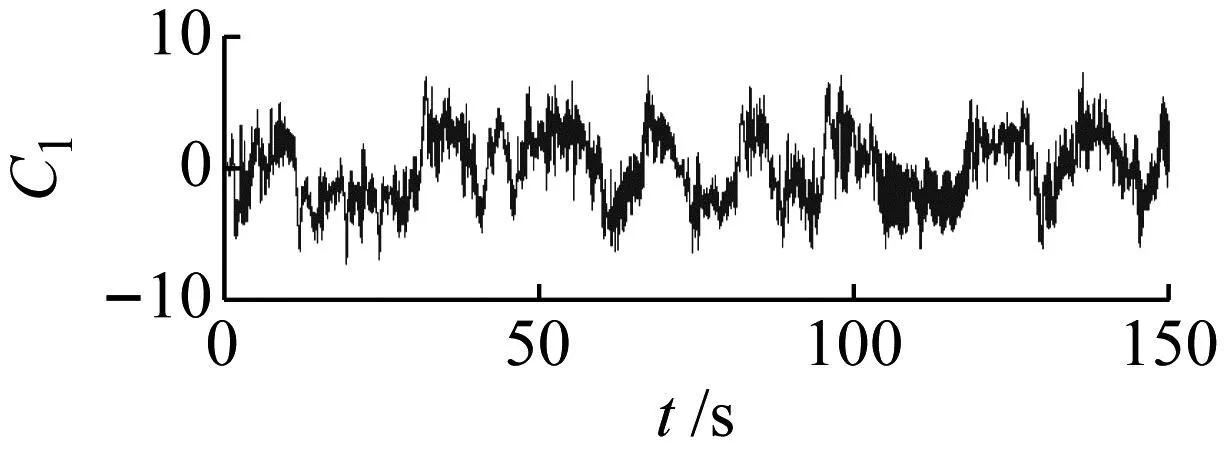
图4 升阻力系数时程

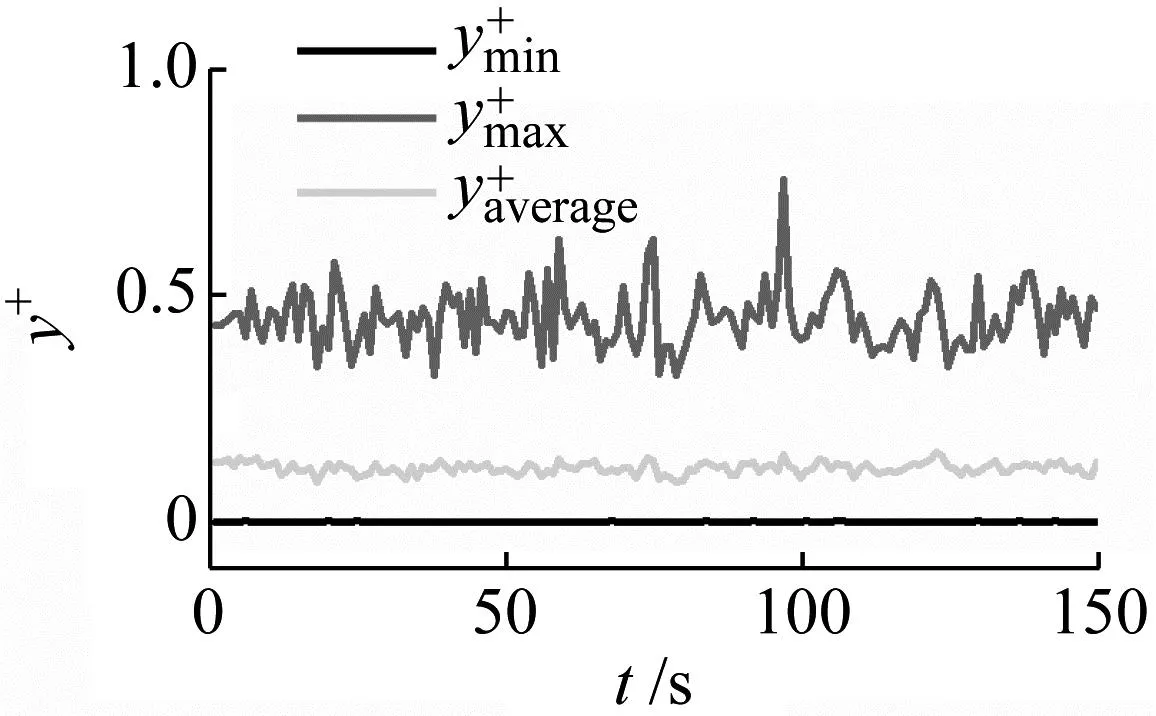
图5 y+时程

将各网格的升力系数均方根、阻力系数均方根列于图7,图中的误差线表示各网格相对于最精细网格(mesh6)的相对误差,虚线表示仅Cluster管子具有边界层,实线表示所有管子具有边界层。由图7可知,随着网格越精细,误差越小,升阻力系数趋于收敛,mesh24的相对误差小于5%。总体来说,网格对阻力系数的影响相对较小,最大相对误差在10%以内,对升力系数的影响较大,最大相对误差达到37%。将各网格相应的所有管子具有边界层与仅Cluster管子具有边界层的结果进行对比,如图8所示。由图8可知,所有管子带边界层的升阻力系数均小于仅Cluster带边界层的情况,两两之间的差异随着网格尺寸的增大而增大,升力系数的差异远大于阻力系数的差异,且所有管子带边界层时,升力系数的统计分布特征更加合理,因此,在管束的流场计算需考虑所有管子的边界层。

(a) 升力系数

(b) 阻力系数

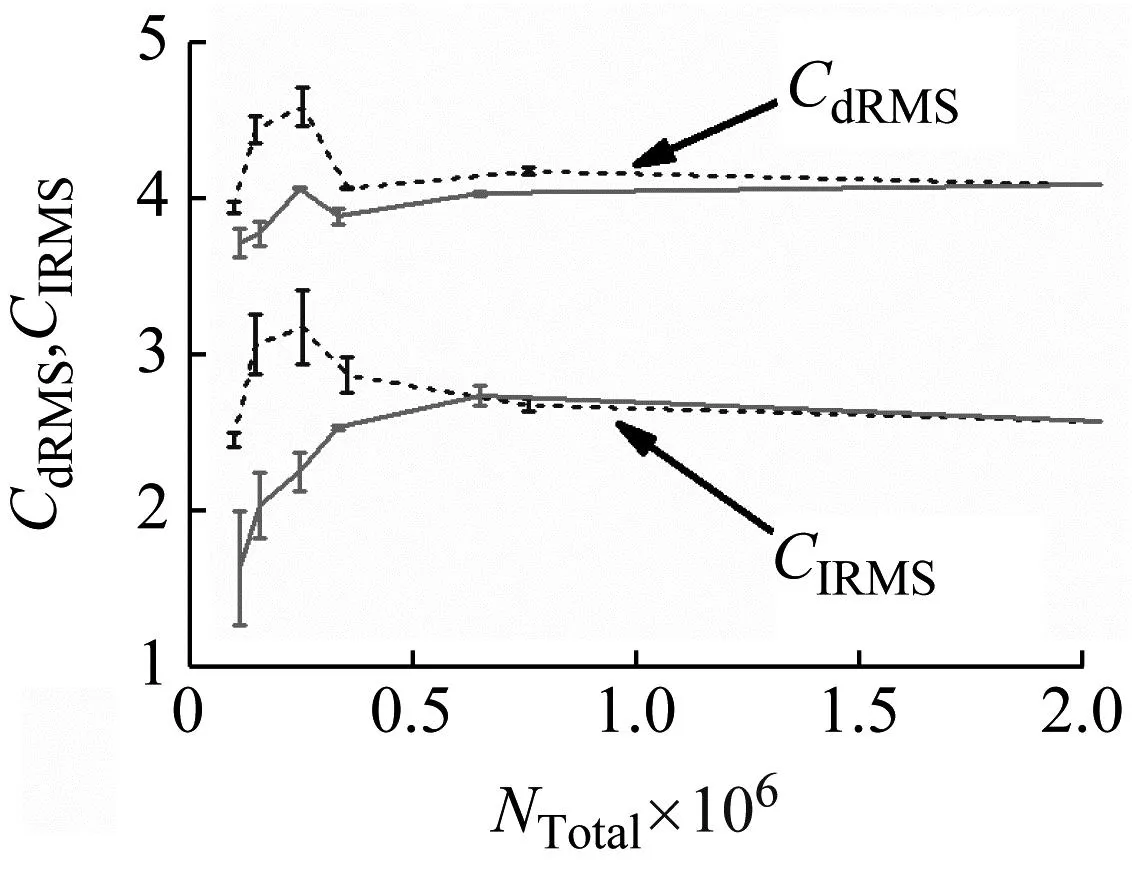
图7 流体力系数随网格的变化情况

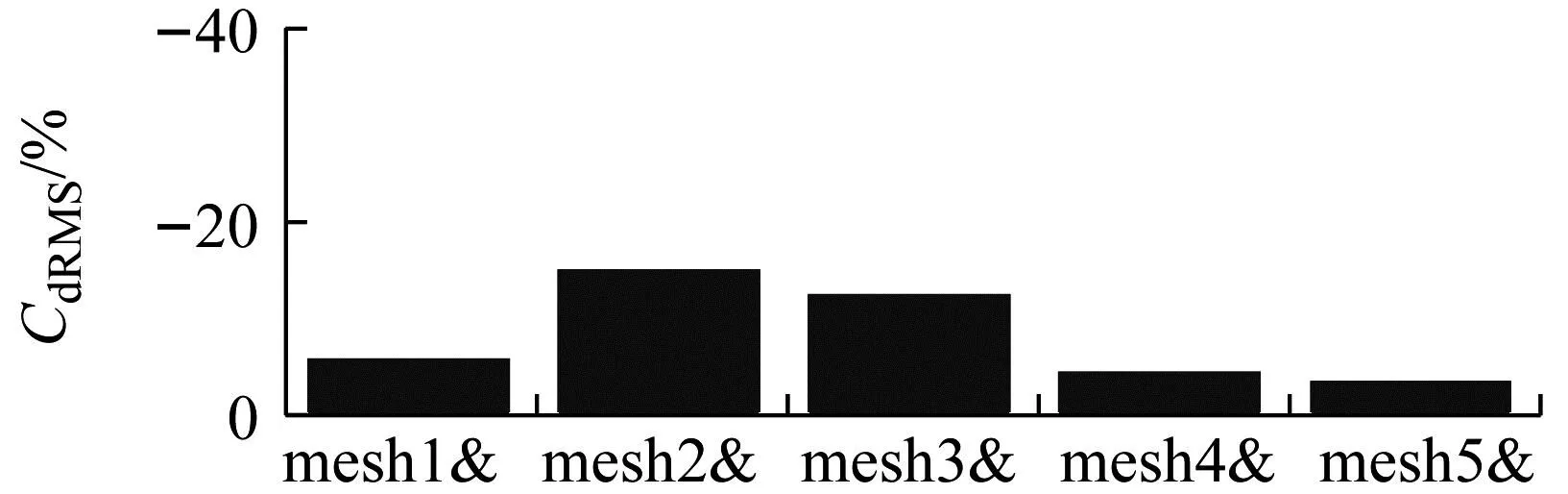
图8 两种边界层网格的对比

2.2 强迫振动下的网格验证

为进一步验证网格独立性,使运动管做强迫振动,按照振幅y0和振荡频率f指定运动

y(t)=y0sin(2πft)

(4)

运动管做强迫振动时的流体力系数随网格的变化情况,如图9所示。同样地,误差线表示各网格相对于最精细网格(mesh6)的相对误差,虚线表示仅Cluster管子具有边界层,实线表示所有管子具有边界层。可以明显看到,在强迫振动情况下,全部管子具有边界层时的误差最小。另一方面,边界层尤其对升力系数影响显著,所有管子具有边界层的升力系数比仅Cluster管子具有边界层的显著减小,且差异总体在20%以上。进一步,通过表2可知,所有管子具有边界层,网格总数的增加并不显著。

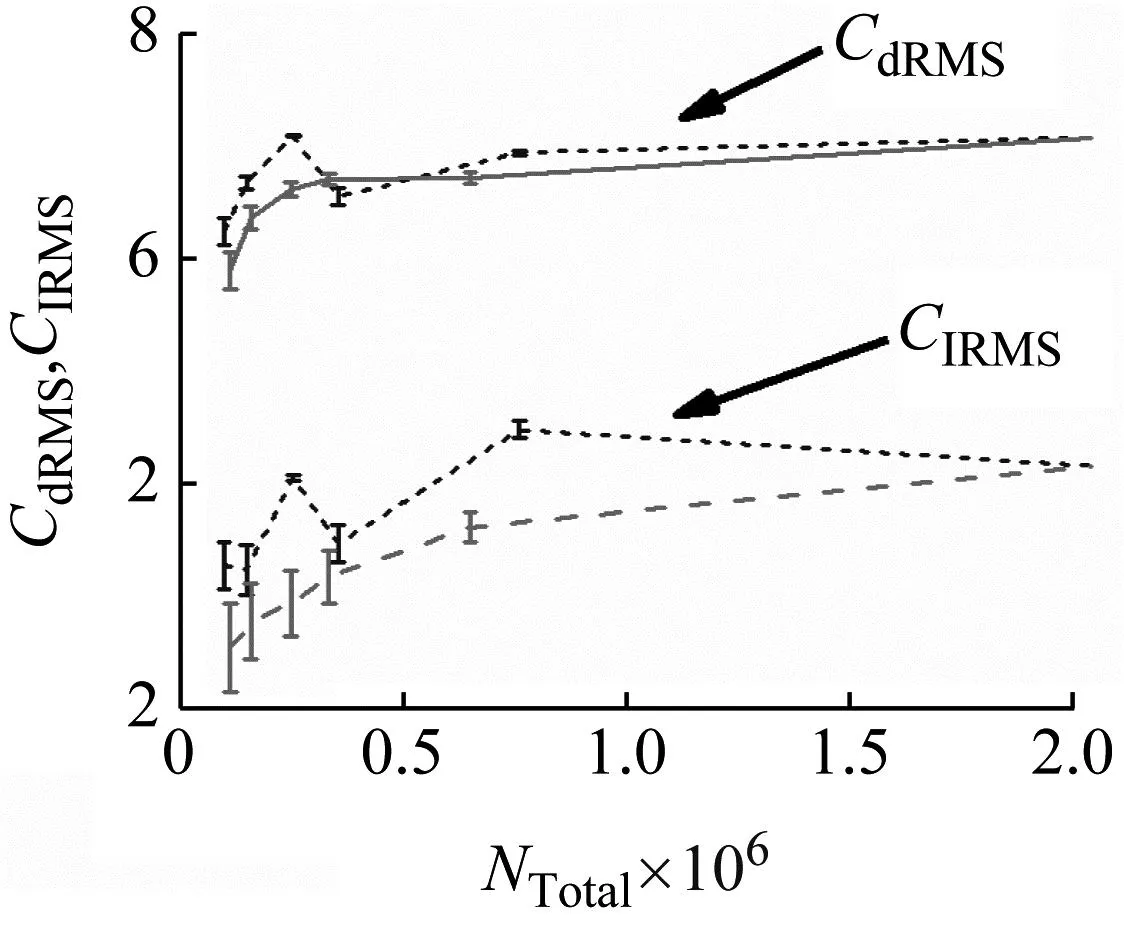
图9 强迫振动时,流体力系数随网格的变化情况

综合静止绕流和强迫振动的结果,选取mesh24(330 000个单元)开展后续研究。

2.3 临界流速预测值对比

进一步,选取较低质量阻尼参数和较高质量阻尼参数两种典型工况进行研究(PMD=0.07和PMD=56.99),其中,PMD=mlδ/ρD2,δ=2πζ,ml为单位管长质量,ρ为流体密度,ζ为阻尼比。入口流速用管子直径和振动频率无量纲化,Ur=Ug/fD,Ug为间隙流速,定义为Ug=U0Pr/(Pr-1),Pr为管束的节径比,U0为入口流速。

采用本文建立的数值模型,使运动管在流体作用下作自由振动,确定临界流速,然后将预测结果绘入稳定性图,如图10所示。并与文献中相似管束的试验结果[8]以及工程验证性试验结果进行对比,可以看到预测结果与试验结果在较大的质量阻尼参数(mass damping parameter, MDP)范围内吻合良好。

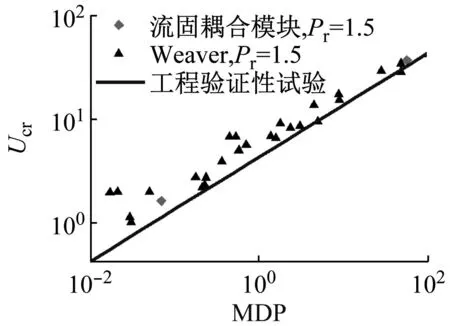
图10 临界流速预测结果与试验结果的对比

3 结果与讨论

管的振动响应根据不同的Ur可以衰减或放大,三种典型的管子响应形式如图11所示。由图11可知,在第一种情况下,系统的净阻尼为正,因此系统是稳定的(见图11(a));在第二种情况下,系统的净阻尼为负,是不稳定的,此时对应于阻尼控制的流弹失稳(见图11(b));第三种情况介于第一种情况和第二种情况,难以仅通过管的响应来判定系统是否失稳(见图11(c))。

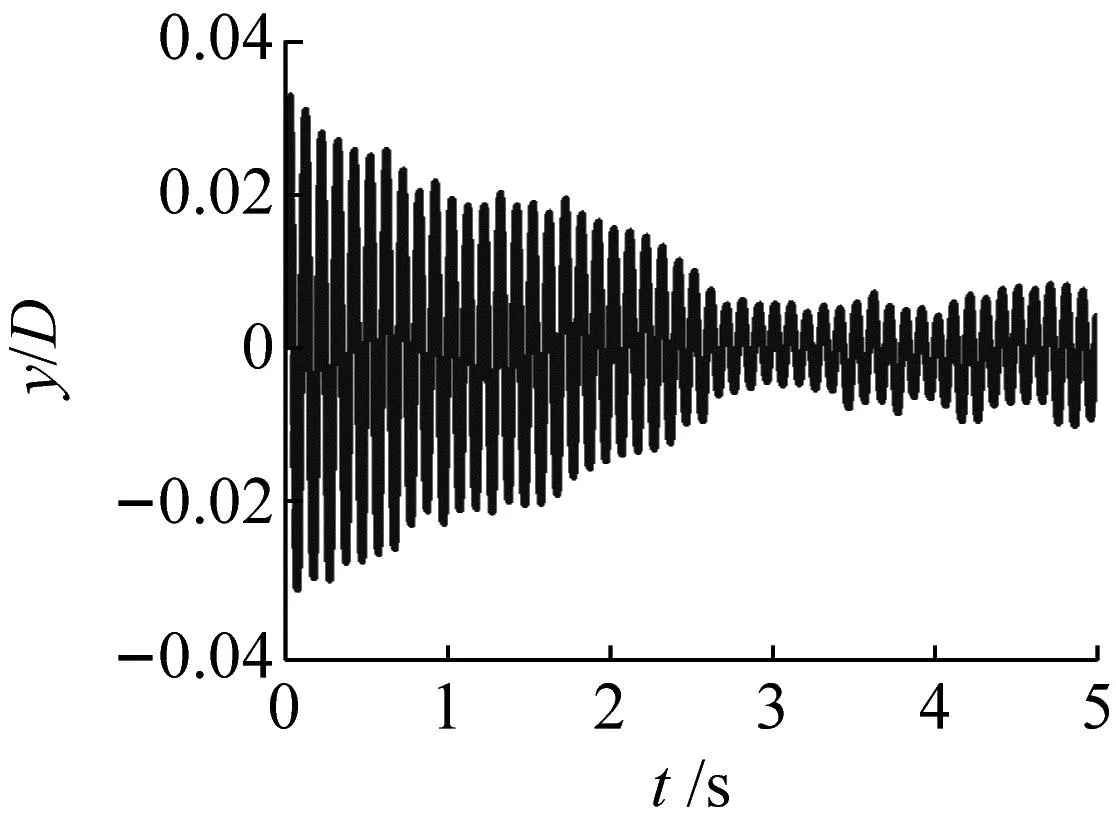
(a) Ur=15

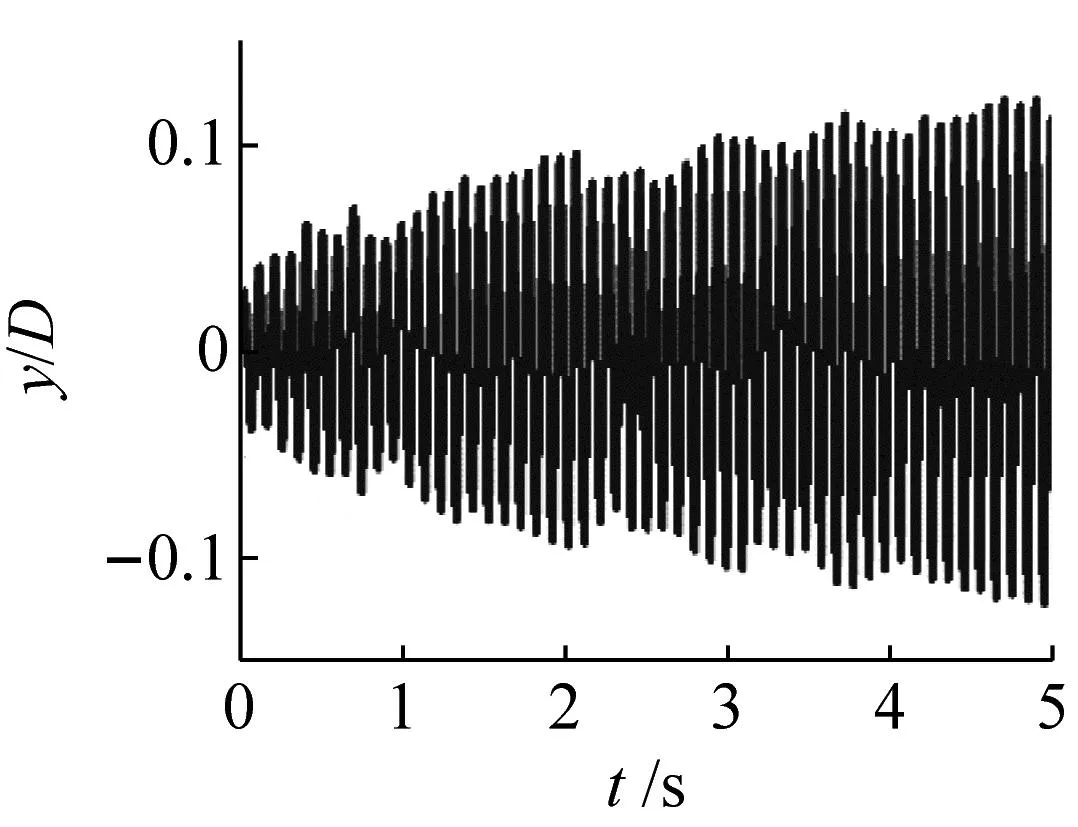
(b) Ur=57

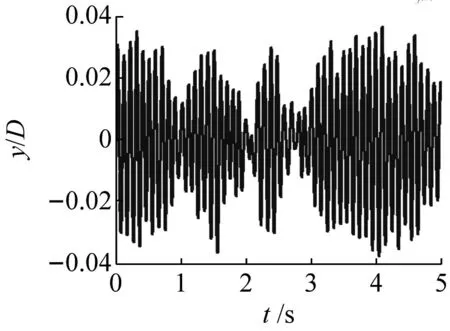
(c) Ur=45

3.1 宏观响应特性

振动位移、流体力等宏观响应是表征管束流弹失稳行为最直观、最常用的方法,如流速超过临界值后,管的振幅会迅速增长,发生所谓的流弹失稳。

升阻力系数、横向位移随速度的变化情况,如图12所示。

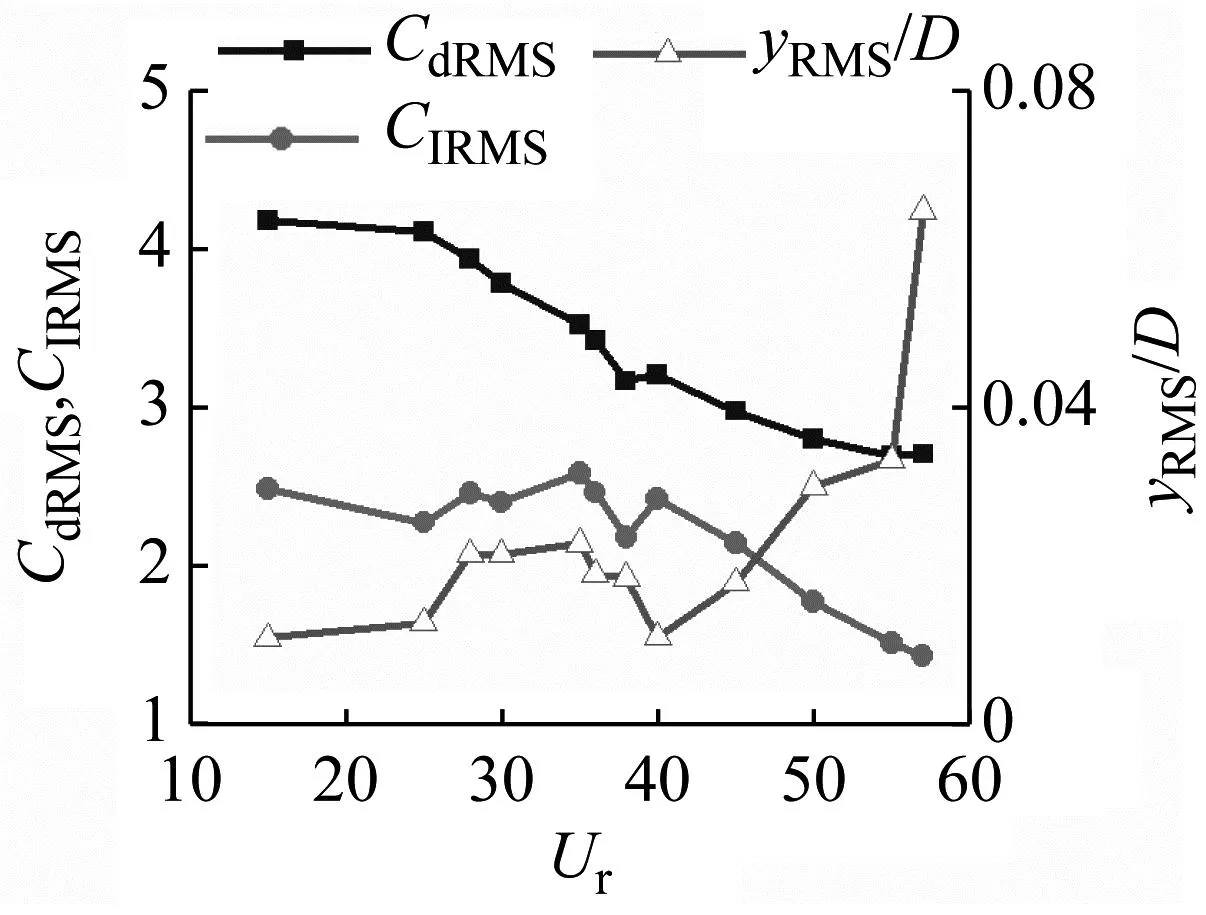
(a) PMD=56.99

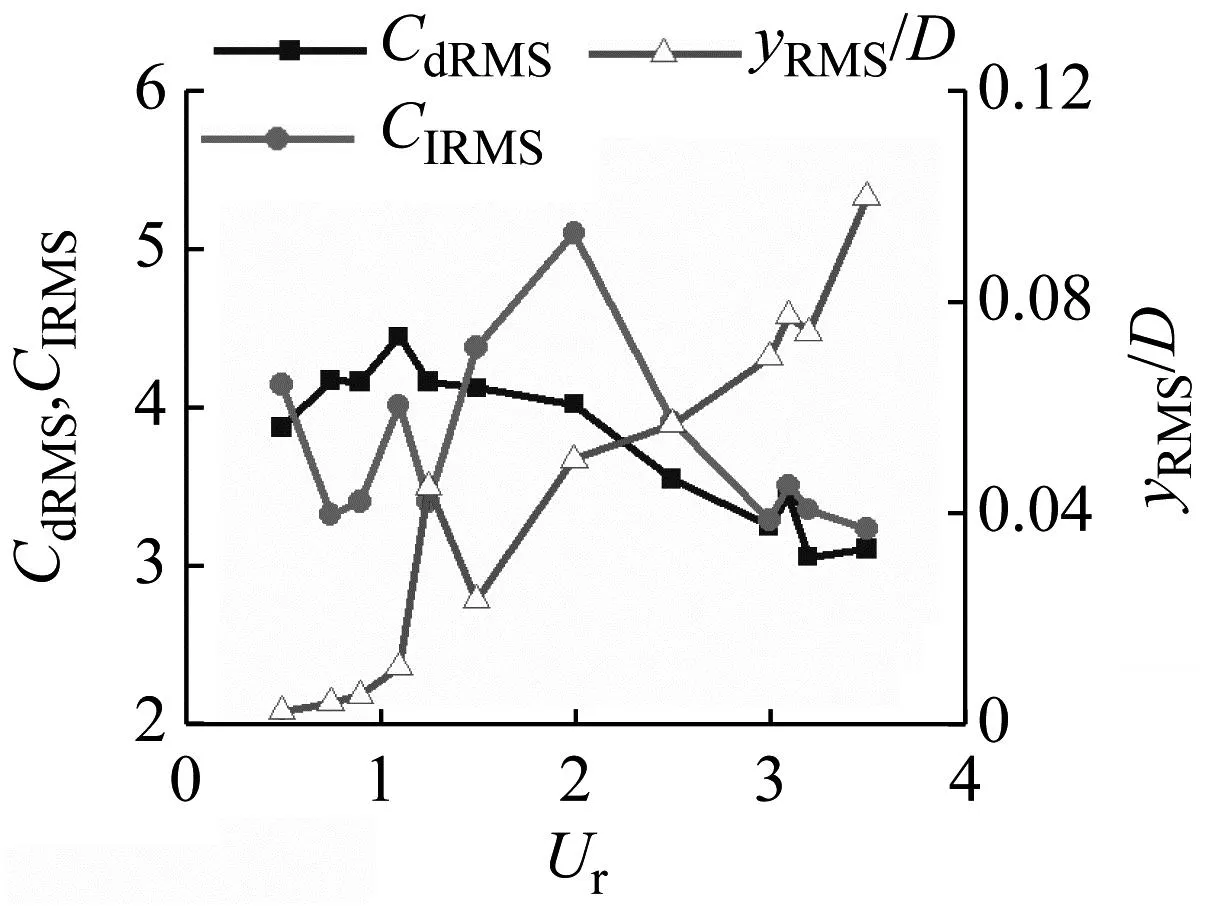
(b) PMD=0.07

由图12可知,总体上,升阻力系数随着流速增大而呈减小趋势,横向位移随着流速增大而呈增加趋势,横向位移并非随着流速变化呈单调关系,这与Weaver早期在水洞中测得的响应形式类似[9]。对于PMD=56.99,在Ur=25～40的速度范围内,出现了一个横向位移的峰值,但通过检查升力的频谱及管的响应频率,发现其并不是漩涡脱落共振,而在Ur=40处,响应曲线的斜率发生了显著变化,相应的升力系数曲线也有一个小幅的增加。对于较小的MDP(PMD=0.07),升力系数波动幅度较大,没有明确的变化规律,横向位移在Ur=1.1时显著增加,在Ur=1.25处出现了一个小的尖峰,但此时管束并没有发生流弹失稳,同样也不是漩涡脱落共振,Ur>1.5后,位移呈持续增长趋势。

由图12可知,流体力系数与横向位移之间明确的相关性,在横向位移变化剧烈的速度处,未发现流体力系数的明显分界点。难以通过振幅-速度曲线的斜率突变点来确定临界流速。

3.2 升力与位移的相关性

为了进一步定量分析升力与位移间的相关性,图13列出了各Ur下的相关系数。在MDP较高的情况下(PMD=56.99),相关系数非常小,说明管子的振动位移不是由于升力直接导致的,说明管的响应是系统的行为。而在MDP较低的情况下(PMD=0.07),升力与位移完全相关,说明振动位移主要来自于升力的强迫振动,也反映出这些工况下系统没有发生流弹失稳。

图13 升力与横向位移间的相关系数

升力与横向位移之间的相干性与相位差,如图14所示。由图14可知,在10 Hz(固有频率)以下,升力与横向位移呈显著相干,相位差趋于0,说明两者同相。在10 Hz附近,相位差发生了从同相到反相的跳跃。在10 Hz以上,不同的MDP显示了不同的相干性与相位差,MDP较大时(PMD=56.99),相干系数逐渐减小到0.5以下,相位差在0～180°之间变化;MDP较小时(PMD=0.07),在约10～20 Hz的频率范围内呈显著相干,相位差约为180°,在约20～100 Hz的频率范围内,相干性先减小再增大,相位差逐渐减小,在约100 Hz以上,呈显著相干且相位差又保持在0°附近。通过分析其它速度下的相干性和相位差,发现差别不大,从相干函数和相位差中,看不出系统发生失稳的明显临界点。

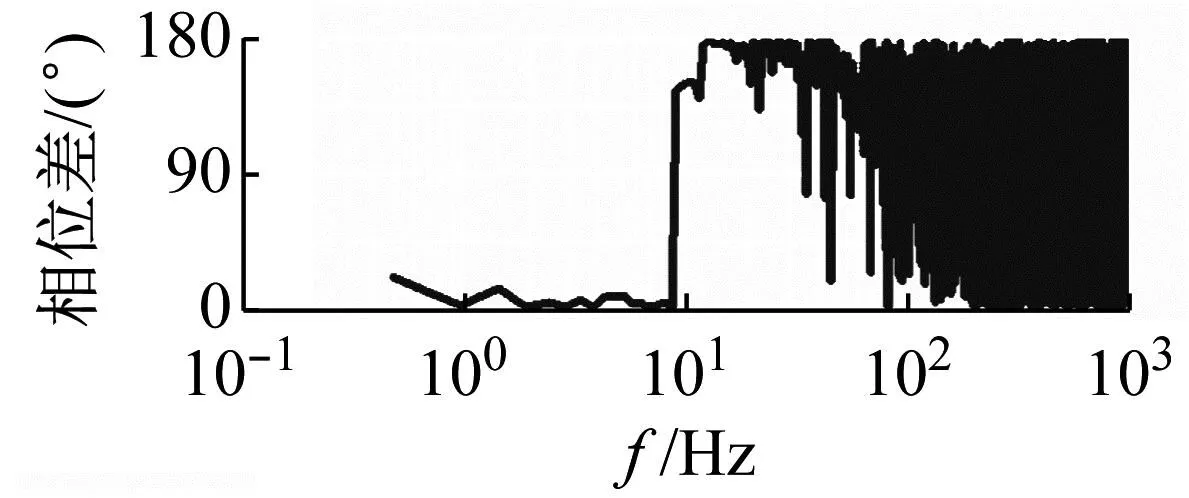
(a) PMD=56.99,Ur=57

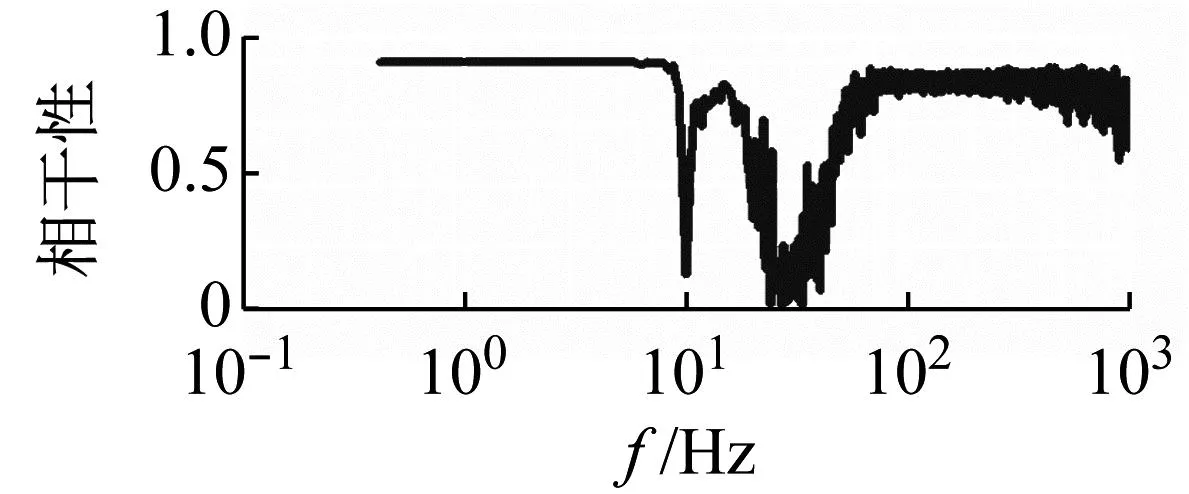
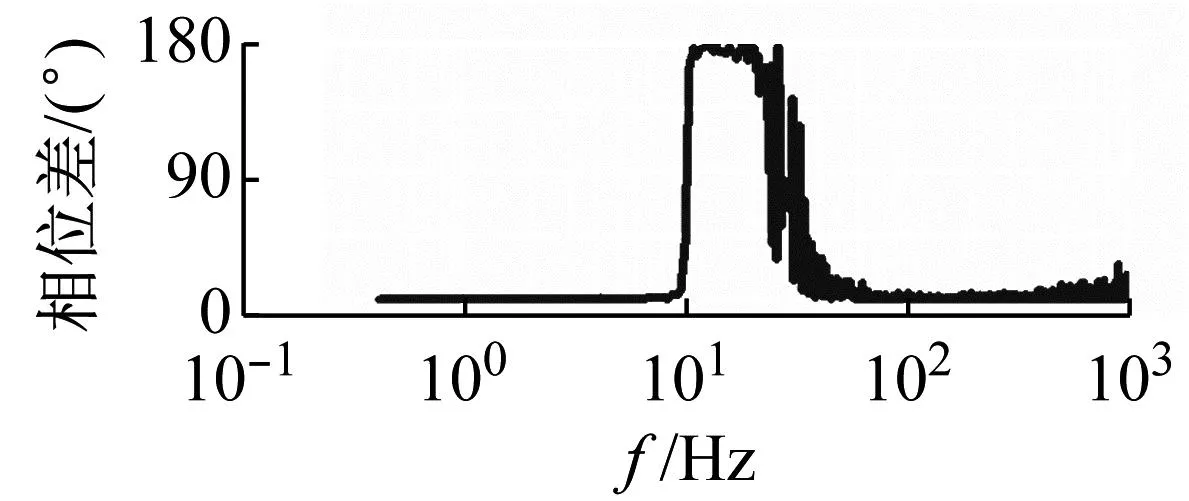
(b) PMD=0.07,Ur=3

3.3 振动能量

进一步通过计算管束流弹系统的能量输入与能量损失,以期得到一些有价值的见解。定义运动管的振动能量为

(6)

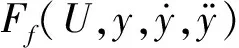
振动能量的时程,如图15所示。其中：W为系统的振动能量;WFf为所有流体力所做的功;WFd为所有耗散力所做的功。可以看到,流速较高时,系统的振动能量为正,说明系统失稳;Ur=45时,系统的振动能量总体上为负,但在某些时刻会变为正,说明此时系统已经具有失稳趋势。系统的振动能量随Ur的变化情况,如图16所示。从图16可知,明显的临界点。与振幅-流速曲线或流体力-流速曲线(见图12)相比,振动能量由于同时考虑了流体力与振动响应,可以更好地反映稳定性。

(a) Ur=45

(b) Ur=57

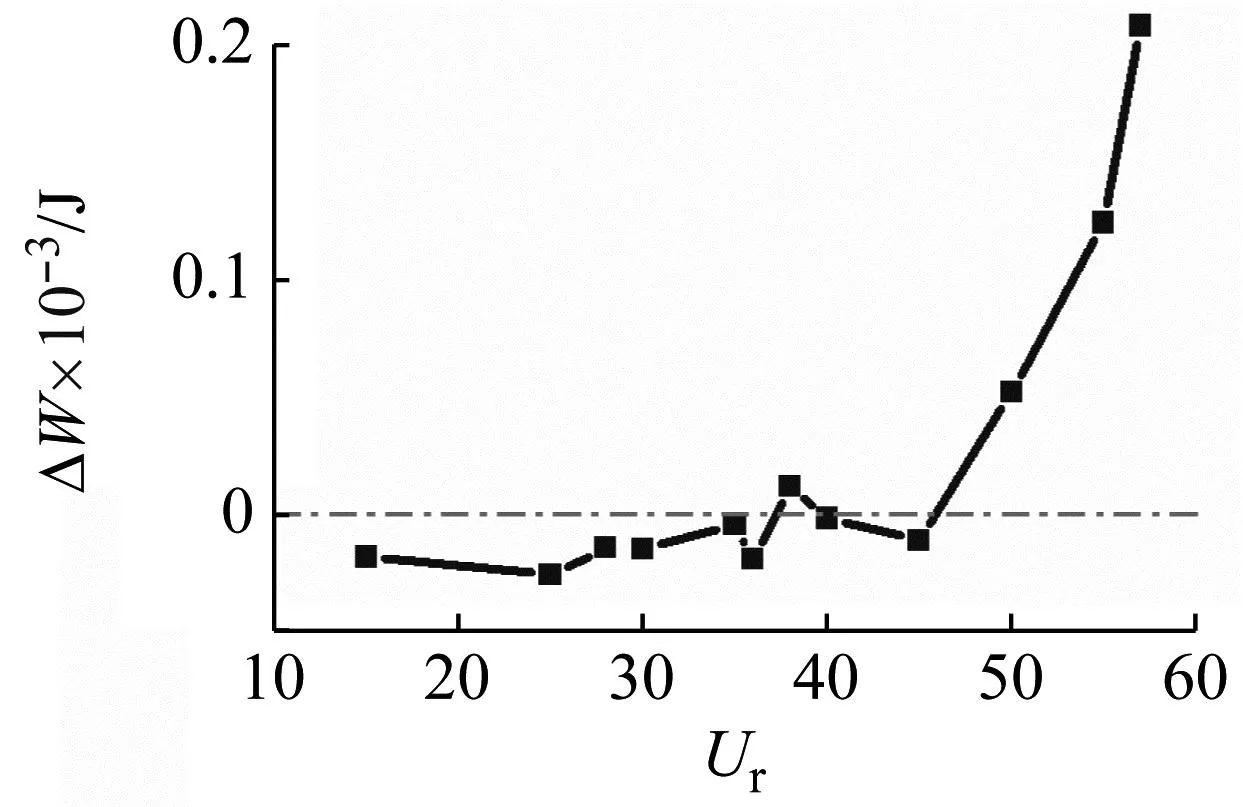
(a) PMD=56.99

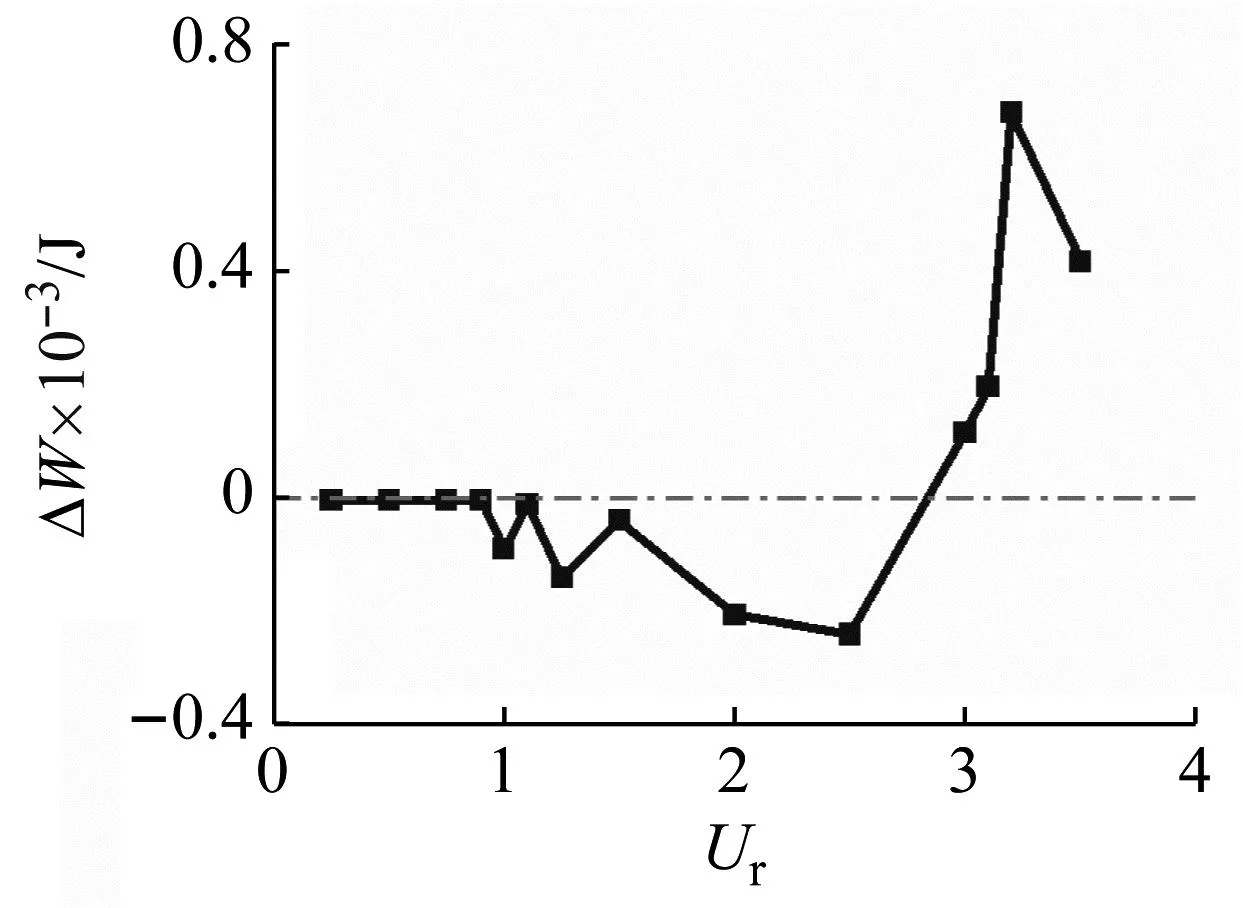
(b) PMD=0.07

3.4 升力的频谱特性

升力系数的频谱如图17～图18所示。当流速和雷诺数较低时,升力系数的频谱为窄带,具有明显的单峰特性(见图17(a));当流速和雷诺数较高时(水中Ur>1.5,基于入口流速的Re=4 500;空气中Ur>25,基于入口流速的Re=5 134),升力系数的频谱开始变为宽带形式,湍流激励或其他激励源是主要激励机理。升力系数频谱特性发生变化的雷诺数与单圆柱绕流时发生转捩的雷诺数(Re=5×103)[10]相当,说明此时流场形式发生了变化,湍流激励增强。

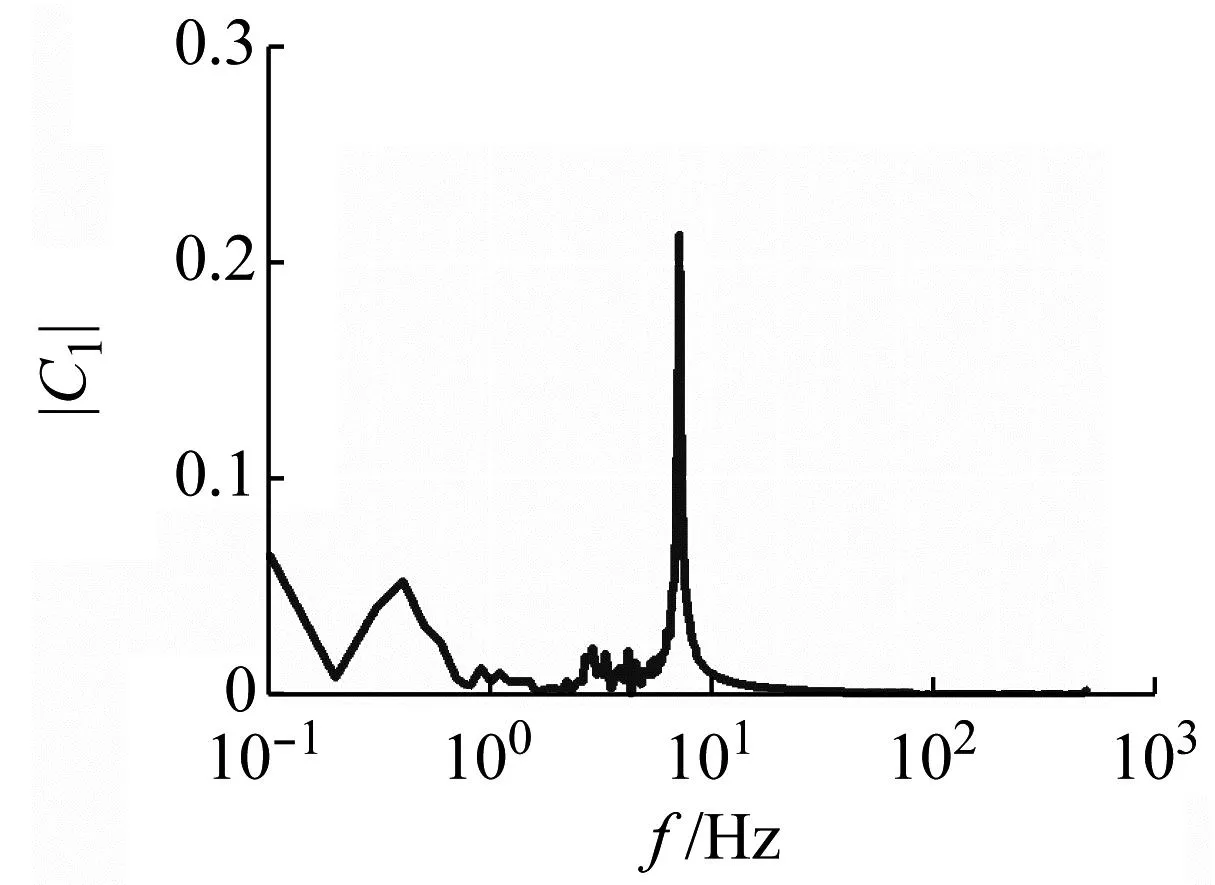
(a) Ur=0.5

(b) Ur=3

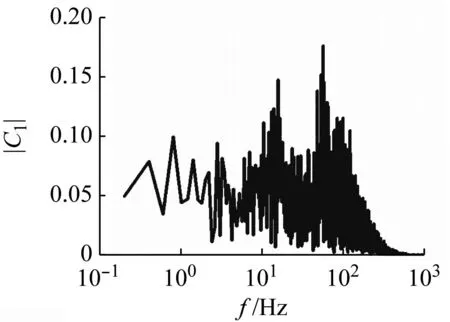
(a) Ur=45

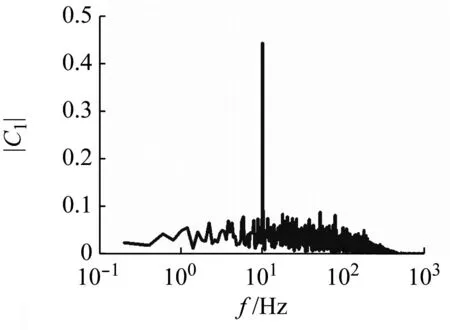
(b) Ur=57

升力的频谱随流速的变化呈现一定规律,如图18所示。对于流体介质为空气的情况(PMD=56.99),在管束发生失稳前存在一个频率区间,在这个区间内,升力系数频谱呈现宽频特性,具有两个较明显的峰,一个对应管子的固有频率,另一个更高的频率对应流体激励频率,随着流速增大,较高频率的峰值也逐渐增大,且逐渐超过管子固有频率对应的峰值;而当系统发生了流弹失稳后,升力系数的频谱从比较宽的频带变到窄带,具有明显的单峰特性(见图18(b))。与空气中不同,水中(PMD=0.07)升力系数的宽频特性主要出现在10 Hz以下(见图17(b))。

3.5 主导激励机理

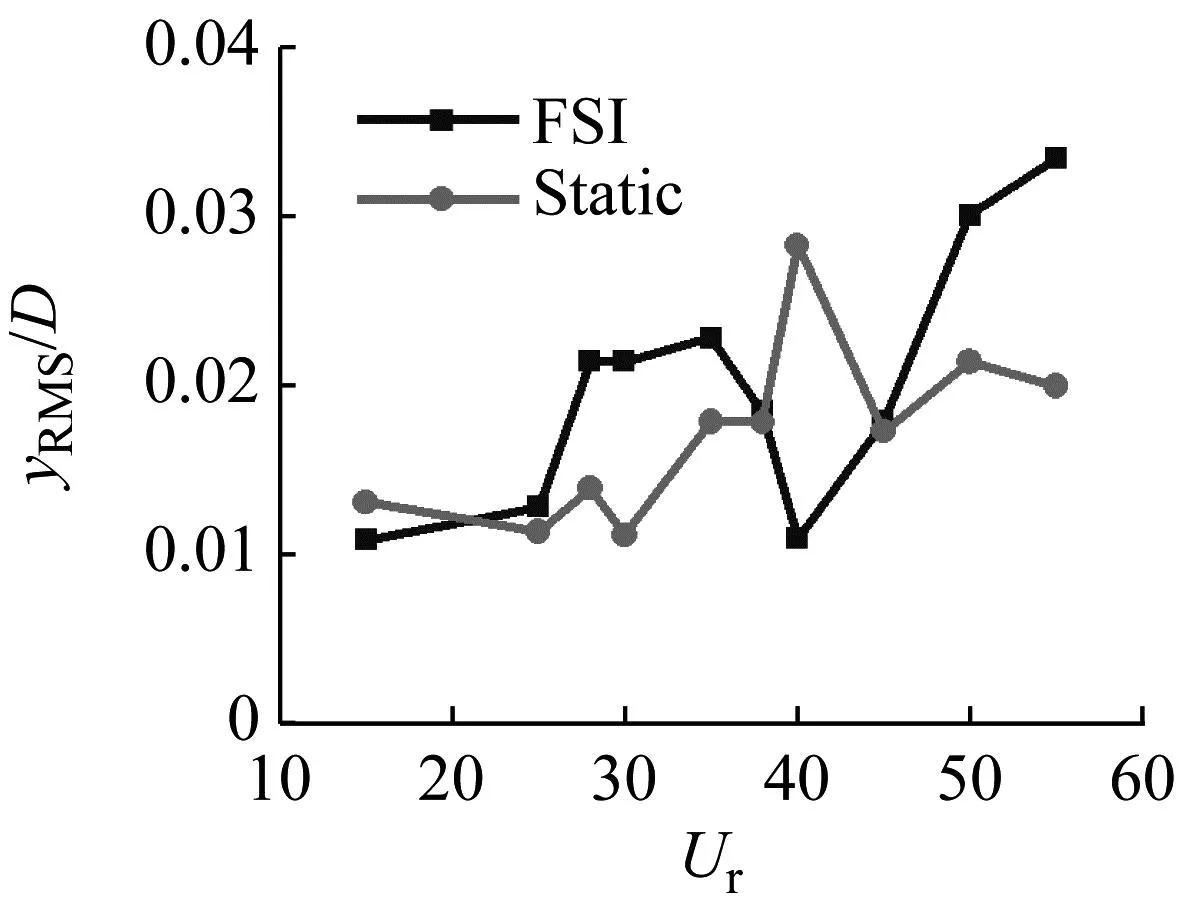
响应特性在Ur=25～40的速度范围内出现了一个横向位移的峰值(见图12(a)),在文中前面的分析中指出,其并不是漩涡脱落共振,同时结合升力频谱的宽带特性可以认为是湍流激励而非漩涡脱落和流弹失稳占主导地位,为了进一步验证这种结论,对比分析了静止绕流和流固耦合的结果,如图19～图21所示。其中FSI表示流固耦合,Static表示静止绕流,静止绕流时管子的响应通过将静止绕流的流体力作用于管的动力学方程,再采用4阶Runge-Kutta法求解而得到。

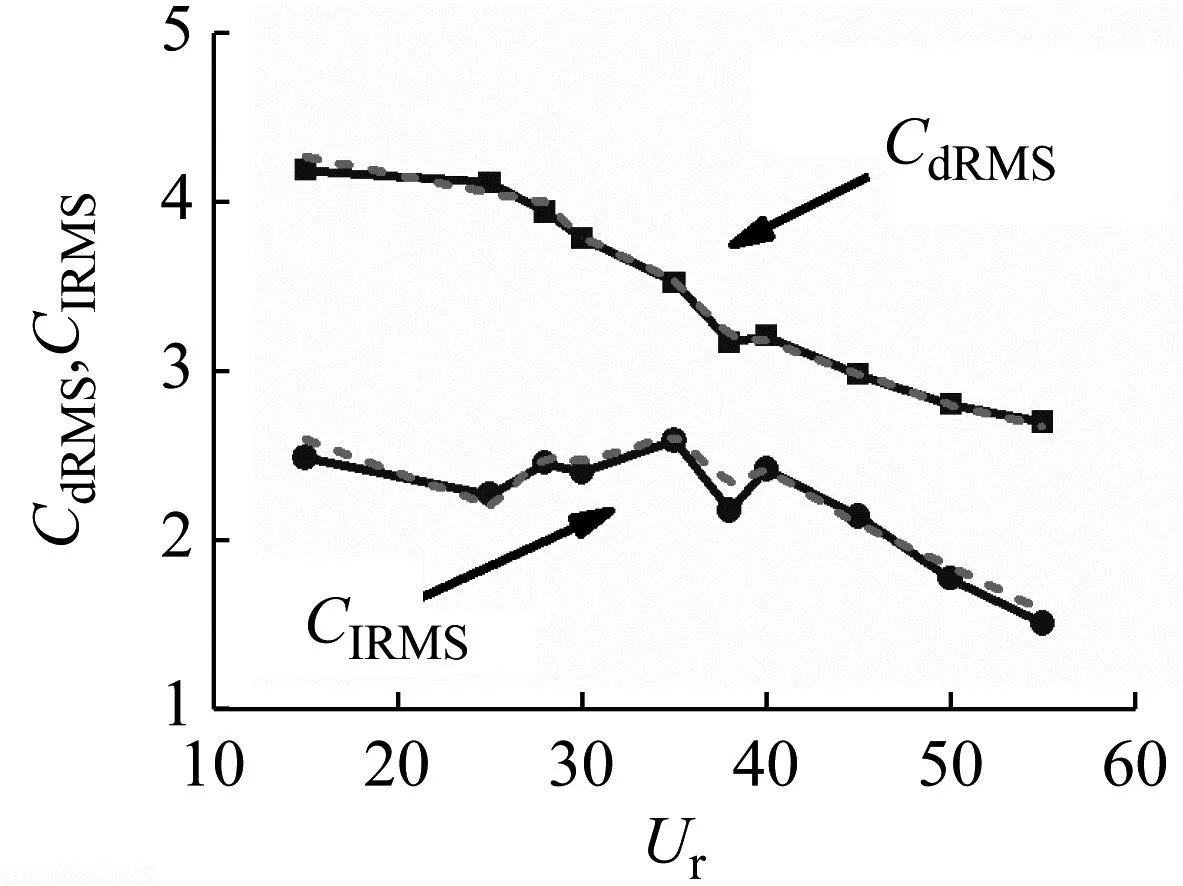
(a) PMD=56.99

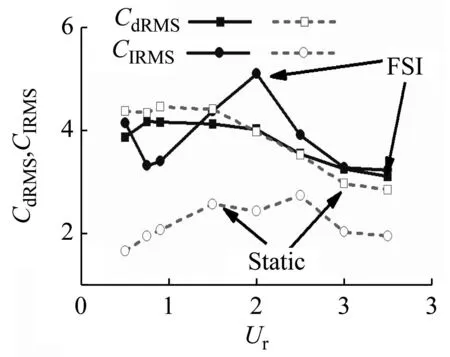
(b) PMD=0.07

从图19可知,PMD=56.99时FSI和Static的流体力几乎相同,说明运动对流体力的影响较小,这也体现在升力与位移间非常小的相关系数上(见图13);而PMD=0.07时,FSI的升力远大于Static的,说明流体-振动耦合对流体力有明显的放大作用,这与弹性管发生涡致振动时振动对流体力的放大作用类似[11]。

横向位移的比较(见图20),对于PMD=56.99,当Ur较小时,主要机理是湍流激励,因此FSI与Static两者相差不大;随着Ur的增大(Ur>40),FSI的位移显著增大,说明流弹失稳逐渐起主导作用。对于PMD=0.07,尽管最大的横向位移已经达到了12%D,但FSI与Static的差别并不大,仅从位移的对比来看,仍然是湍流激励占主导地位,从振动能量的对比更可以清晰地反映这些特征(见图21)。通过对比静止绕流下的强迫振动与流固耦合振动,同时结合升力的频谱特性、系统的振动能量,可以更全面地反映出占主导地位的激励机理。

(a) PMD=56.99

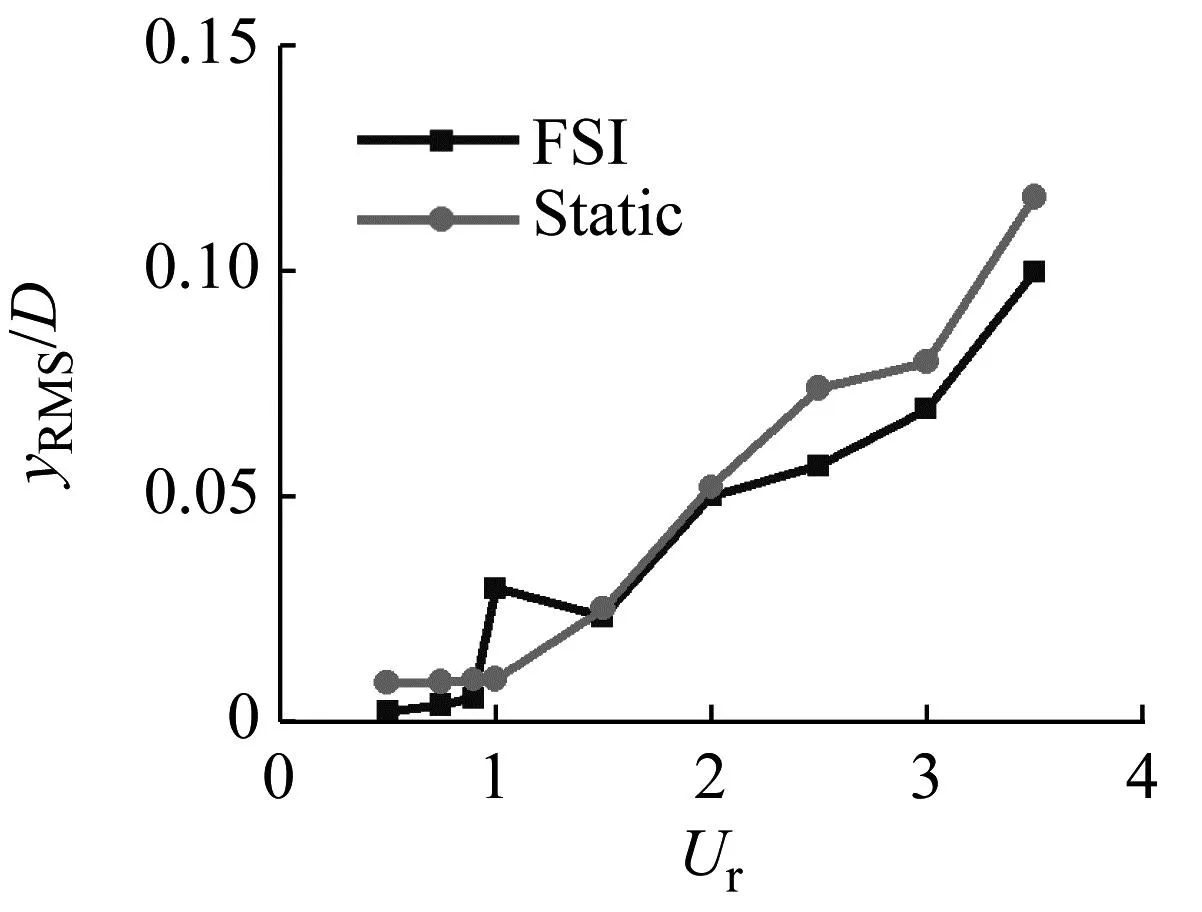
(b) PMD=0.07

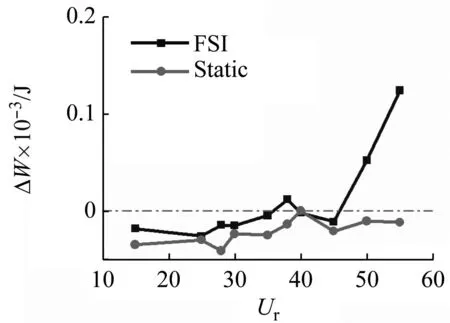
(a) PMD=56.99

(b) PMD=0.07

4 结 论

本文基于开源CFD工具OpenFOAM,建立了平行三角形管束的阻尼控制型流弹失稳预测模型,分析了影响阻尼控制型不稳定机制的关键参数和流动响应,主要结论如下：

(1) 难以通过振幅-速度曲线的斜率突变点、升力与位移的相关性来确定临界流速,而振动能量综合考虑了流体力与振动响应,可以更好地反映管束流弹系统的稳定性特征。

(2) 在MDP较高的情况下,升力与横向位移间的相关系数非常小,说明管子的振动位移不是由升力直接导致,管的响应为系统行为;而在质量阻尼参数较低的情况下,升力与位移完全相关,说明振动位移主要是升力的强迫振动。

(3) 当雷诺数较低时,升力频谱为窄带,具有明显的单峰特性;当雷诺数较高时,升力频谱变为宽带形式,主导激励机理是湍流激励;升力频谱特性发生变化的雷诺数与单圆柱绕流时发生转捩的雷诺数相当;当系统发生了流弹失稳后,升力频谱从宽带变到窄带。

(4) 通过对比静止绕流下的强迫振动与流固耦合振动,同时结合升力频谱特性与系统的振动能量,可以更为全面地反映出系统中占主导地位的激励机理。