多层剪切型支撑钢框架整体稳定性的解析算法研究

兰树伟, 周东华, 陈 旭, 毛德均

(1.昆明学院 建筑工程学院,昆明 650214; 2.昆明理工大学 建筑工程学院,昆明 650500)

剪切型支撑钢框架结构体系是钢结构工程中常用的结构形式,支撑体系的变形主要是剪切变形,常见的有交叉斜杆和单斜杆支撑等。钢结构与混凝土结构相比,具有截面尺寸小、构件细长等特点,随着建筑高度的增加,钢结构的稳定问题变得格外凸出,必须加以重视和研究。在剪切型支撑钢框架结构设计中总希望能有便于运用的结构临界力解析计算公式,以避免复杂的有限元整体计算或校核有限元计算结果的正确性。目前GB 50017—2017《钢结构设计标准》[1](简称规范)中给出了有侧移(无支撑)和无侧移(强支撑)框架柱的计算表格,尚无确定弹性侧移框架柱(即：弱支撑框架柱)计算长度系数的内容。剪切型支撑钢框架结构整体稳定性计算,与剪切型支撑所提供刚度强弱程度的有关,须要考虑同层柱间的相互支援和层与层之间的支援作用,还须要考虑支撑与钢框架之间的相互作用,目前规范还无法解决这些问题。为了解决这些问题,李国强等[2]给出了确定任意支撑钢框架柱计算长度系数的计算公式,其计算过程复杂需求解超越方程。Aristizabal[3-4]在有限元分析的基础上给出了不同约束条件下柱计算长度系数近似计算公式,给出了使柱达到无侧移失稳的最小支撑刚度。童根树等[5-6]利用平衡法研究了非完全支撑框架结构的稳定性,基于部分支撑柱稳定方程,给出了框架柱支撑的门槛刚度计算公式,提出了一种确定剪切型支撑框架稳定性的假想荷载法。金路等[7]基于有限元Ansys分析变形对应的荷载水平与其承载力之间的关系,提出了一种计算钢框架-支撑结构稳定和二阶侧移的直接分析法。Ma等[8]基于层抗侧刚度分析结构楼层稳定性,提出了一种评估具有半刚性连接的部分支撑钢框架稳定性的简化方法。剪切型支撑框架有些楼层支撑所提供的刚度大能够达到强支撑刚度的要求,有些楼层支撑弱所提供抗侧刚度较小无法满足强支撑刚度的要求而属于弱支撑楼层,剪切型支撑与钢框架之间的相互作用也加大了剪切型支撑框架整体稳定临界承载力解析计算的难度。本文分析了剪切型支撑的抗侧刚度与结构临界力之间的关系,推导了层临界支撑刚度的计算公式,基于任意支撑下框架柱临界内外刚度比系数的计算公式,利用该系数将求解剪切型支撑框架临界承载力的二阶问题转化为计算结构的楼层有效抗侧刚度的一阶问题,使得结构临界力的求解大为简化。

1 剪切型支撑刚度与结构临界力之间的关系

1.1 支撑抗侧刚度

如图1(a)带有剪切型支撑的多层多跨钢框架,支撑的作用可以等效为楼层横梁处的水平弹簧,如图1(b)所示。

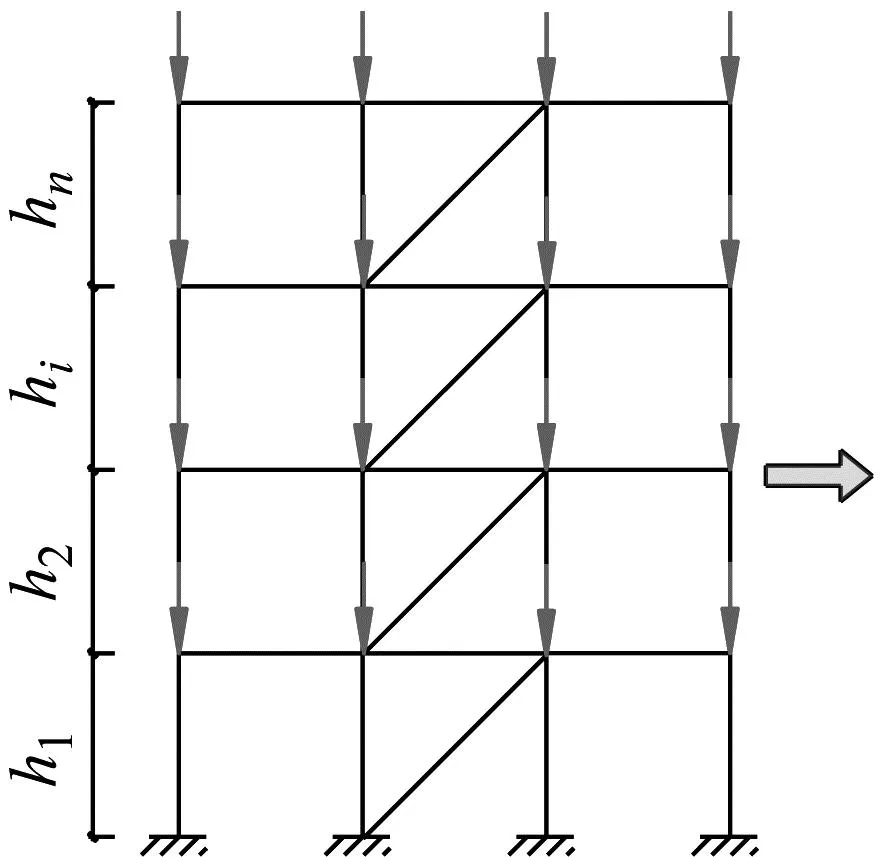
(a) 剪切型支撑钢框架

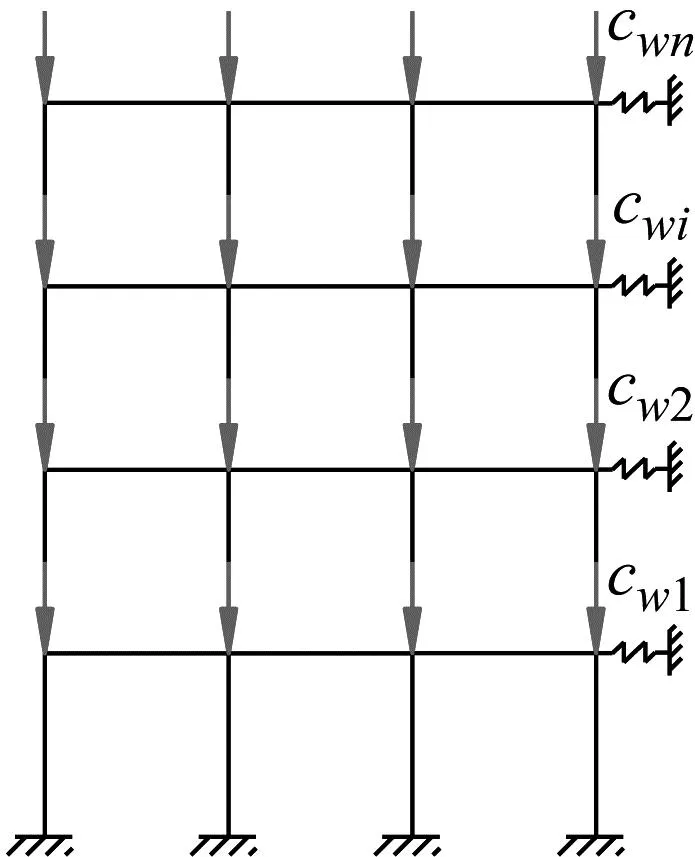
(b) 等效简图

利用剪切型支撑杆件的变形协调条件结合杆件的受力分析可得任意层支撑抗侧刚度的计算式[9]

(1)

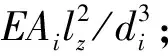
1.2 支撑抗侧刚度与结构临界力的关系

取图1(a)所示的一个三跨四层单斜杆支撑钢框架,层高和跨度均为4 000 mm,框架梁柱均采用HW200×200×8×12,支撑采用等边角钢,弹性模量E=206 kN/mm2,框架只承受作用在梁柱节点上的荷载,各层各节点上作用荷载均为100 kN,假定失稳时各柱同时达到临界荷载,变化单斜杆支撑角钢规格,采用有限元Ansys进行弹性屈曲计算,分析该支撑钢框架临界力的变化。如表1所示。

表1 剪切型支撑钢框架的临界承载力对比分析

从表1可以看出,当不设置单斜杆支撑时(类型①),即支撑抗侧刚度为零,钢框架临界承载力最小,此时属于无支撑自由侧移钢框架,发生有侧移屈曲;随着支撑斜杆面积增大,从类型②～⑥,支撑的抗侧刚度也随之增加,支撑钢框架临界承载力也逐渐增加,属于弱支撑弹性侧移钢框架,发生有侧移屈曲;从类型⑦～⑨,支撑抗侧刚度增加显著,但临界力基本没有增加,仅增加了0.2%,可以看出当支撑抗侧刚度增加到一定程度,进一步增加支撑刚度无法提高结构临界承载力,属于强支撑无侧移钢框架,发生无侧移屈曲。从类型①～⑨,支撑刚度逐渐增加,支撑钢框架从有侧移失稳逐渐过渡到无侧移失稳,定义有侧移失稳的临界荷载与无侧移失稳的临界荷载相等时的支撑刚度为临界支撑刚度。类型⑨支撑刚度约是类型⑦的4倍,此时支撑所提供刚度超过临界支撑刚度很多,但该部分刚度对提高结构临界承载力无帮助,属于冗余刚度,该部分刚度未激活,仅当支撑刚度小于临界支撑刚度,此时刚度才完全激活,称为有效刚度,增加支撑刚度才能提高结构临界承载力。目前的研究主要针对单根柱的临界支撑刚度,而剪切型支撑钢框架结构杆件众多且存在层与层之间的相互作用,如何求解层支撑临界刚度,计算剪切型支撑钢框架结构临界承载力还有待进一步研究。

2 层临界支撑刚度

对于剪切型支撑钢框架结构,钢框架柱受到剪切型支撑的水平支撑作用,利用分离柱法[10]将需分析的局部柱从整体结构中分离出来,每根分离柱的柱端约束都可采用三个弹簧来模拟,如图2所示。分离柱柱顶作用一侧移刚度为cw的水平弹簧以模拟剪切型支撑对钢框架柱的支撑作用,分离柱的柱顶和柱底受到转动约束,采用两个转动弹簧来模拟,刚度分别为c1和c2。

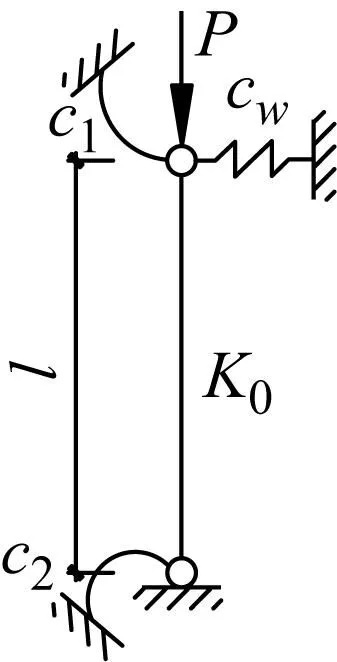
图2 分离柱的三弹簧模型

图2所示剪切型支撑钢框架三弹簧分离柱的稳定特征方程[11]为

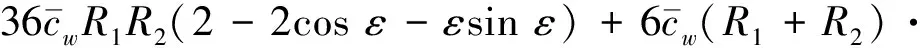
6(R1+R2)ε4cosε-ε5sinε=0

(2)

(3)

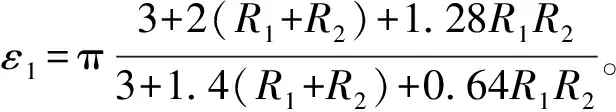
图3 框架柱临界支撑刚度诺模图

剪切型支撑钢框架第i层层临界支撑刚度cwTi为该楼层所有钢柱临界支撑刚度之和,可按照下式进行计算

(4)

层临界支撑刚度是衡量楼层支撑刚度是否处于激活状态的重要指标。只有支撑所提供刚度小于层临界支撑刚度,支撑刚度才完全处于激活状态,才是有效刚度;当剪切型支撑提供的楼层支撑刚度大于层临界支撑刚度时,超出层临界支撑刚度的部分,处于未激活状态,该部分刚度的增加无法进一步提高结构临界承载力,属于无效刚度。

3 任意支撑柱的临界刚度比系数

对于剪切型支撑钢框架,由于杆件众多,若直接利用平衡法求解,特征方程将更为冗长,求解将变得更为困难,因此需要寻找便于应用的求解方法。

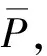
(5)

式中：λ为临界因子,数值上λ=Pcr/P,当结构处于临界状态时λ=1.0;α为临界刚度比系数,对于柱水平支撑刚度介于零与临界支撑刚度之间,第i层第j根弱支撑钢框架柱的临界刚度比系数可采用下式进行计算[13]

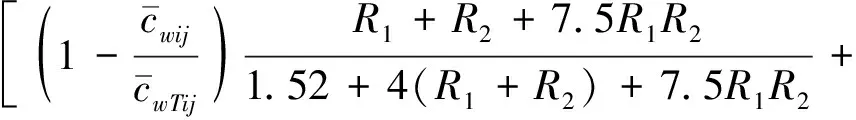
(6)

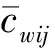
(a) 分离柱的扩展结构

(b) 弹簧-摇摆柱

(7)

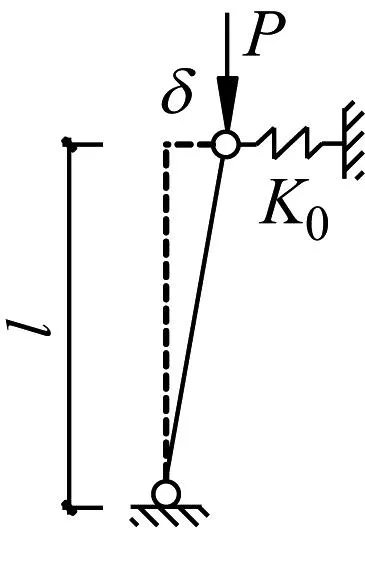
由于式(7)计算无侧移框架柱临界刚度比系数冗长应用较为不便,故绘制无侧移框架柱临界支撑刚度比系数诺模图,如图5所示。

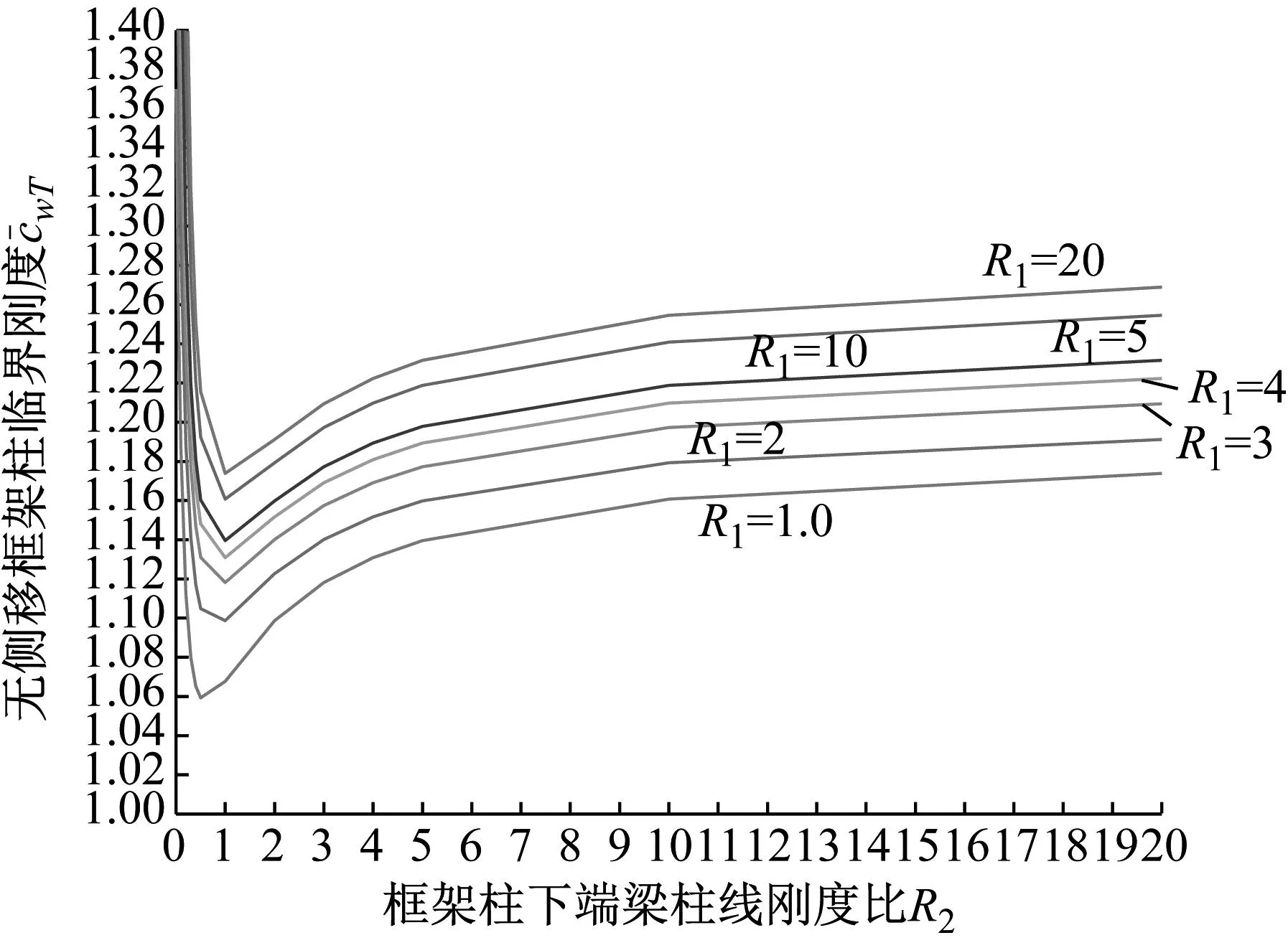
图5 无侧移框架柱临界刚度比系数诺模图

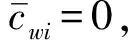
(8)

式(8)计算自由侧移框架柱临界刚度比系数应用较为不便,故绘制自由侧移框架柱临界刚度比系数诺模图,如图6所示。

图6 自由侧移框架柱临界刚度比系数诺模图

剪切型支撑钢框架的三弹簧分离柱的抗侧刚度为上下转动约束柱抗侧刚度与水平弹簧刚度的叠加,计算式如下[14]

(9)

同理对于剪切型支撑钢框架第i楼层的抗侧有效刚度ki应为该楼层所有框架柱抗侧刚度与该层支撑有效刚度的总和,即：

(10)

式中：EIj为第i层第j根钢柱抗弯刚度;R1j和R2j分别为第i层第j根柱上、下端横梁线刚度之和与柱线刚度之和的比值;hi为第i层层高;m为第i层钢柱总根数;cwi为第i层层支撑有效刚度,当cwi>cwTi时,超出层临界支撑刚度部分为无效刚度,无法提高临界承载力,故仅考虑有效支撑刚度部分,取cwi=cwTi。

从式(5)可以看出,当确定了剪切型支撑钢框架柱抗侧有效刚度和临界刚度比系数后,很容易求解得到不同屈曲模态下支撑柱的临界承载力,其虽能考虑剪切型支撑与框架柱的相互作用,但对于剪切型支撑钢框架存在同层柱的相互支援以及层与层之间的支援作用是无法考虑的,容易造成不合理设计,若将弹簧-摇摆柱中的水平弹簧替换为剪切型支撑钢框架,求解整体结构的临界刚度比系数又异常困难,因此,有必要寻找能考虑这两种支援作用的剪切型支撑钢框架结构临界承载力的求解方法。

4 剪切型支撑钢框架临界承载力计算公式

计算剪切型支撑框架临界承载力时,当剪切型支撑所提供刚度超出层临界刚度部分属于无效刚度,计算时取层临界刚度,按此刚度确定支撑钢框架层临界力有侧移和无侧移两者计算相等,故计算剪切型支撑钢框架结构各层的整体抗侧有效刚度,可参照有侧移结构将每层抗侧有效刚度视为一个弹簧,剪切型支撑钢框架整体抗侧有效刚度可视为每个弹簧的串联,因此,剪切型支撑钢框架第i层的整体抗侧有效刚度Ki与层抗侧有效刚度关系式为

(11)

式中,Ki为第i层的整体抗侧有效刚度,k1,k2,…,ki为各层的抗侧有效刚度,按式(10)计算。

由式(5)可得剪切型支撑钢框架第i层荷载刚度kPi为

(12)

式中：αij为第i层第j柱的临界刚度比系数,可由式(6)～(8)计算或通过查诺模图5～图6求得;Nij为第i层第j柱的轴力;mi为第i层柱的总根数。

按照剪切型支撑钢框架结构整体抗侧有效刚度的求法,结合式(12)将各层荷载刚度进行串联可得剪切型支撑钢框架结构整体荷载刚度计算公式

(13)

式中：KPi为第i层的整体荷载刚度;λi为第i层临界因子。假定各柱的轴力均按比例加载,则存在：Nij=ξijNmin,其中,ξij为比例系数,Nmin为最小轴压力。

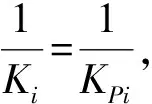
(14)

由式(14)可求出剪切型支撑钢框架临界承载力,所求各层的临界因子λi相等,即各层荷载刚度将各层抗侧有效刚度同时消耗为零发生失稳而未产生层间相互支援,这种情况在实际工程中很少出现。若不考虑各层之间的支援作用而直接按此计算剪切型支撑钢框架临界承载力,容易造成不合理的设计。为了考虑这种不同楼层之间的支援作用,将式(14)所求出的层临界因子λi按照层轴力权重加权平均的方法[15]求出剪切型支撑钢框架结构整体临界因子λ,得到修正后的剪切型支撑钢框架整体稳定临界承载力的计算公式

(15a)

(Nij)cr=ξij(λNmin)

(15b)

式中：Ni为第i层各柱轴力之和;λi为第i层的临界因子,由式(14)求得,最小层临界因子λmin所在楼层为薄弱层;λ为剪切型支撑钢框架结构的整体临界因子,通过层临界因子与结构整体临界因子的相对大小及比例关系可以定量地分析不同楼层之间的支援作用;(Nij)cr为第i层第j根钢柱的临界力;ηi为轴力权重参与系数,经过有限元回归分析得到其与层临界因子和最小层临界因子比值的幂函数关系

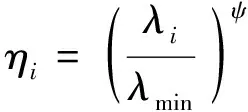
(16a)

(16b)

由式(15b)求得剪切型支撑钢框架柱临界承载力后,可根据式(17)计算求得各柱的计算长度系数。

(17)

式中,μij为第i层第j根钢柱的计算长度系数。

5 算 例

图7所示的四跨六层剪切型支撑钢框架公共建筑,剪切型支撑采用交叉斜杆,顶层由于建筑功能需要取消支撑。框架柱采用方箱型柱200 mm×8 mm,顶层梁采用HN248×124×5×8,其余各层梁采用HN300×150×6×9,交叉斜撑采用等边角钢L75×6 mm(1～3层)、L40×4 mm(4～5层),层高h为400 cm,各跨跨度为400 cm,弹性模量E=20 600 kN/cm2,荷载P为100 kN,用本文方法求解该剪切型支撑钢框架结构临界力及各层填充示意柱计算长度系数。

图7 四跨六层交叉支撑钢框架及轴力、二阶效应系数

本文求解步骤：

步骤1由式(1)可求得各层剪切型支撑抗侧刚度cwi,由式(4)求得层临界支撑刚度cwTi,比较两者的大小关系,根据式(10)计算各层抗侧有效刚度ki,结果列入表2。

步骤2由式(6)～式(8)或查诺模图5和图6求得各柱的临界刚度系数αij,详见图7。由式(12)计算剪切型支撑钢框架各层荷载刚度kPi,结果详见表2。

步骤3由式(11)求得结构各层整体抗侧有效刚度Ki,由式(13)计算结构各层整体荷载刚度KPi;由式(14)求得各层层临界因子λi,由式(16)求得各层轴力权重参与系数ηi,代入式(15a)求得结构整体临界因子λ,结果列入表2。

步骤4由式(15b)求得各柱临界力(Nij)cr,由式(17)确定剪切型支撑钢框架结构各柱的计算长度系数,结果详见表2。

为了便于比较分析,用本文方法和有限元Ansys分别进行了计算,Ansys求解时柱和梁均采用BEAM188单元,交叉斜撑采用LINK1单元,节点均为刚接,进行弹性屈曲分析,相关计算结果列入表2,忽略轴向变形的影响。

本文方法计算剪切型支撑钢框架柱的临界承载力和计算长度系数与有限元Ansys计算结果相比误差均在5%以内,计算精度较好,表明考虑了交叉斜撑与钢框架柱的相互作用、同层柱的相互支援以及层与层之间的支援作用,弥补了规范法无法确定弱支撑弹性侧移类型钢框柱计算长度系数的不足。

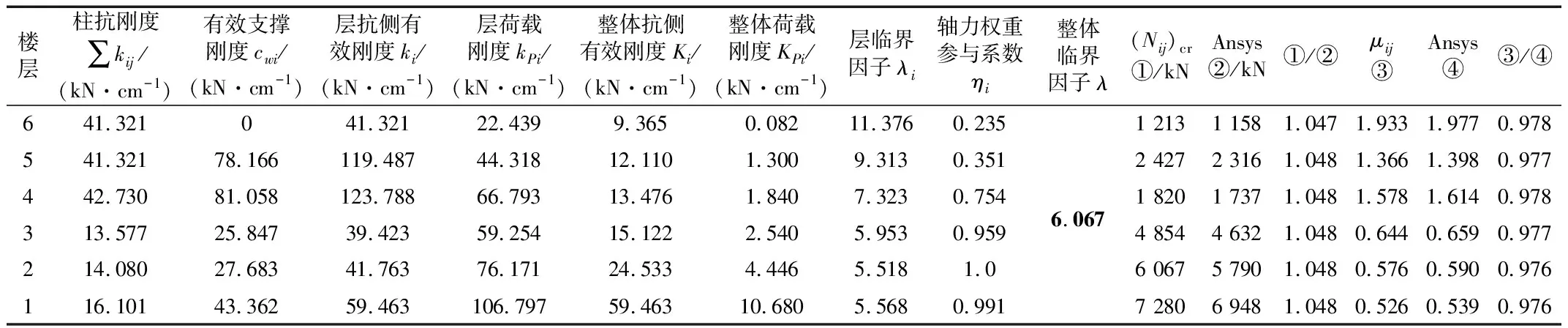
表2 剪切型支撑钢框架柱临界力及计算长度系数对比结果

本算例整体结构临界因子λ=6.067,剪切型支撑钢框架层临界因子的最小值所在楼层为第二层,表明该层为结构薄弱层,该层临界因子为5.518,该层从刚度富裕楼层获得支援,提高了该层结构临界承载力,提高比例为10%;该结构一层～三层层临界因子均小于结构整体临界因子,表明该三层结构无刚度富裕,从刚度较大楼层获得刚度支援,临界承载力有所提高;四层～六层层临界因子大于结构整体临界因子,表明该三层有刚度富裕,为刚度较小楼层提供了刚度支援,临界承载力有所降低,其中六层虽未设置交叉斜撑但刚度富裕程度最高,主要是由于该层轴力小,荷载刚度对层抗侧刚度消耗程度低,对薄弱层的支援有限。

6 结 论

(1) 提供了一种能较为准确地求解剪切型支撑钢框架整体稳定临界承载力的解析算法,既能考虑剪切型支撑对钢框架柱的支撑作用,也能很好地考虑同层柱的相互支援以及层与层之间的支援作用,可以弥补目前《钢结构设计标准》无法确定弱支撑框架柱计算长度系数的不足。

(2) 分析层支撑刚度与层临界支撑刚度可以判断剪切型支撑提供刚度的激活程度,有多少属于激活的有效刚度,有多少属于未激活的无效刚度。当剪切型支撑提供的抗侧刚度大于层临界支撑刚度后进一步提高该层的支撑刚度,无法提高结构临界承载力。

(3) 分析楼层临界因子和整体结构临界因子可以判断出结构薄弱层所在位置,提供了一种分析剪切型支撑钢框架结构层与层之间支援作用的计算方法,能够看出那些楼层提供支援,那些楼层获得支援,可以定量地计算楼层临界承载力的提高程度。