一字型剪力墙计算长度分析
李 伦
(广东省建筑设计研究院 广州 500010)
0 引言
在现代高层剪力墙或框架-剪力墙住宅中,一字型剪力墙的使用变得愈来愈多,但在结构底部往往会有几层通高的情况,基于安全性考虑,方案或者初步设计时为满足《建筑抗震设计规范:GB 50011-2010》[1](以下简称《抗规》)中关于一字型剪力墙高厚比的要求,往往将底部加强区剪力墙做得很厚,大大影响观感。若按《高层建筑混凝土结构技术规程:JGJ 3-2010》[2](以下简称《高规》)计算满足稳定性要求,剪力墙高厚比要求可以适当放松,但《高规》中关于一字型剪力墙计算长度系数仅给出一个定值,若出现墙肢周边楼板存在大开洞或剪力墙有洞口[3]的情况,在《高规》[2]中并未有明确条文说明,应进行专门分析。
1 计算长度系数影响因素及计算方法
根据薄壳屈曲理论[4-6],剪力墙计算长度系数主要影响因素为楼板支撑条件和剪力墙自身刚度。
现从楼板与墙肢长度比值,楼板与剪力墙线刚度比,剪力墙开洞率三个方面入手,对一字型剪力墙进行屈曲稳定分析,进而得出计算长度系数的变化规律。
剪力墙计算长度系数通过欧拉公式[7,8]进行计算:

则计算长度系数:

式中:I 为构件在屈曲方向的惯性矩;L 为构件长度;根据临界荷载Pcr可反算计算长度系数。
2 有限元分析
2.1 软件计算结果正确性验证
本文采用有限元软件SAP2000[9]对一字型剪力墙进行屈曲稳定分析,模型分别按有楼板、无楼板两种情况,得到计算长度系数后与规范值对比,验证软件计算结果的准确性。
模型参数如下:C40 混凝土剪力墙,弹性模量[10]为E=3.25×104N/mm2,层高 4 m,墙厚 t=0.3 m,墙长 6 m;C30 混凝土楼板,弹性模量为 E=3.00×104N/mm2,板厚t=0.11 m,板尺寸:6 m×3 m。
支座约束条件:无楼板模型顶部节点仅约束水平向变形,墙底部按铰接;有楼板模型中剪力墙底部及楼板支座均按铰接[11,12]。
根据SAP2000 屈曲分析结果得到临界屈曲荷载Pcr,然后反算计算长度系数μ,模型及屈曲变形如图1所示。
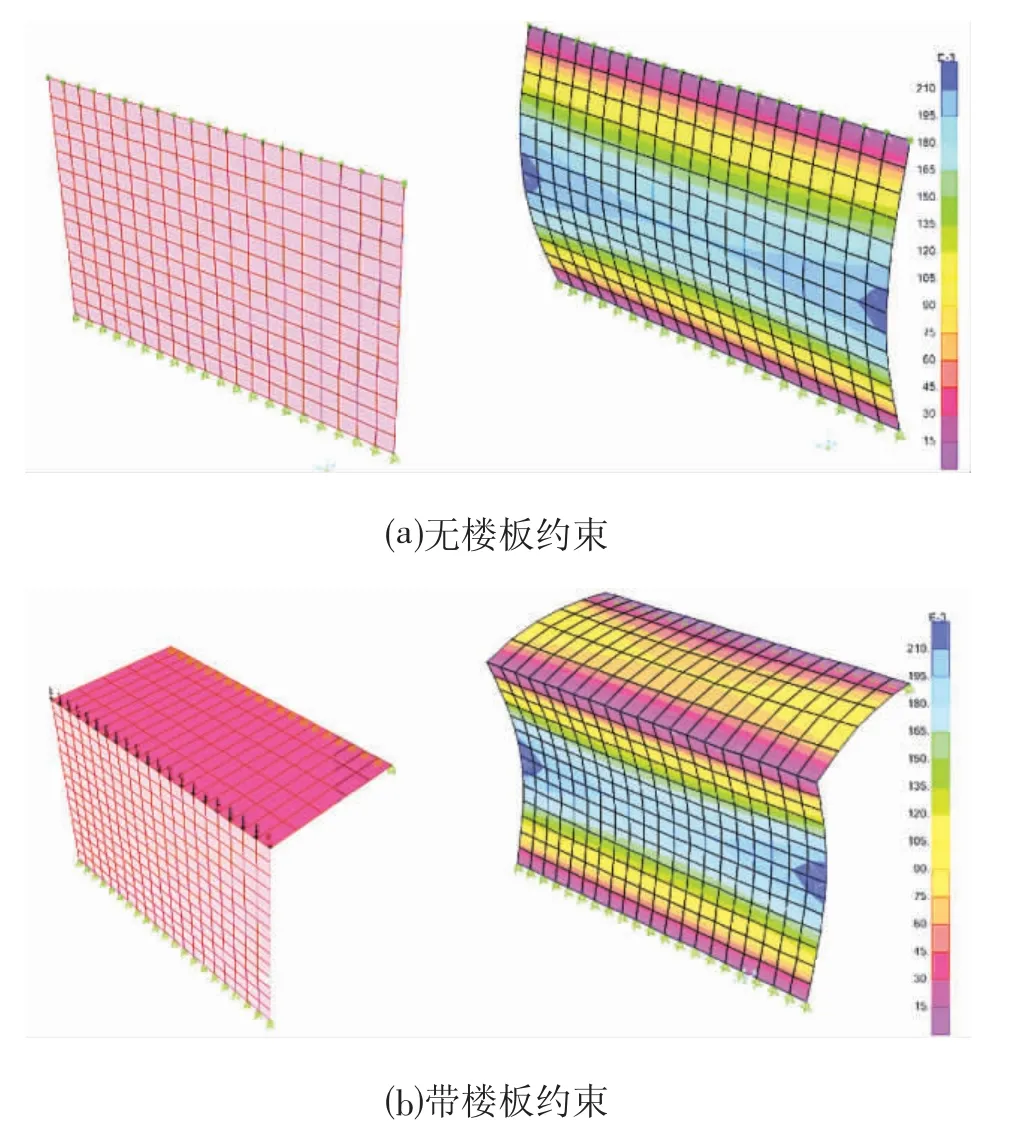
图1 剪力墙屈曲分析Fig.1 Buckling Analysis of Shear-wall
无楼板、有楼板的计算长度系数μ 分别为1.00、0.98,规范限值为1.00。
可以看出,无论有无楼板约束,一字型剪力墙计算长度系数均接近规范限值,证明软件计算结果及计算过程均准确,同时也说明楼板约束能减少剪力墙计算长度系数。
2.2 楼板与墙肢长度比值对计算长度系数影响
SAP2000 计算模型参数同2.1 节带楼板模型,通过调整楼板与墙肢长度比值η 来分析计算长度系数μ 的变化情况。
楼板开洞模型如图2、图3所示。
计算长度系数μ 随η 变化如图4所示。
从图4可以看出,楼板长边长度与墙肢长度比值η ≥0.40 时,计算长度系数μ 基本能维持在1.0 左右,此时基本能够满足规范值1.0 的要求;当η<0.40 时,计算长度系数μ 发生显著变化,峰值达到1.762,此时远远大于规范1.0 的限值要求,计算长度系数要放大计算,实际应用的时候要尽量避免η<0.40 的情况。
由图4的变化趋势线(虚线)所示,给出拟合公式:


图2 楼板开洞模型示意Fig.2 Floor Opening Model
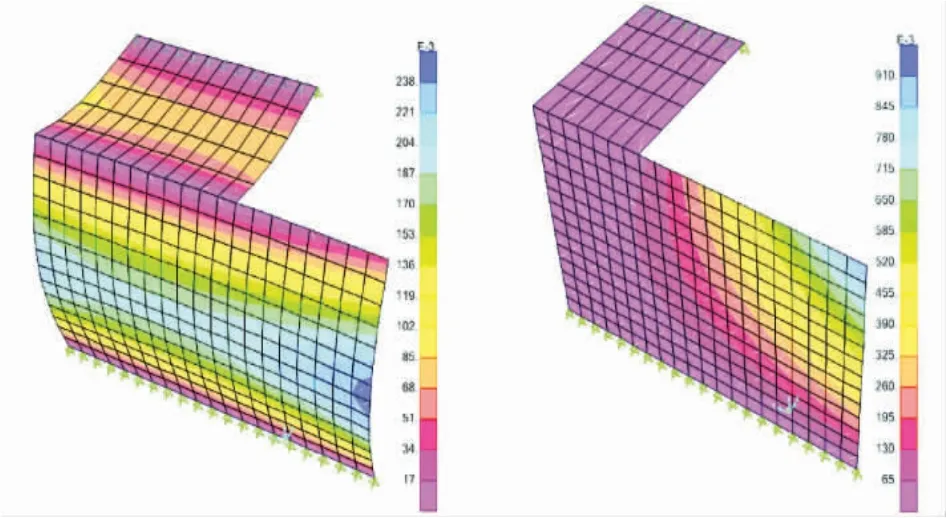
图3 屈曲分析Fig.3 Buckling Analysis

图4 计算长度系数μ随η变化图Fig.4 Effective Length Coefficient μ Changes with η
2.3 楼板与剪力墙线刚度比对计算长度系数影响
由2.1 节可知,楼板对剪力墙起到约束作用,本节通过研究楼板与剪力墙线刚度比K=i板/i墙,定量分析一字型剪力墙计算长度系数μ 的变化规律。SAP2000计算模型参数同2.1 节带楼板模型,通过调整板厚及墙厚来调整K 值。
模型如图5所示。
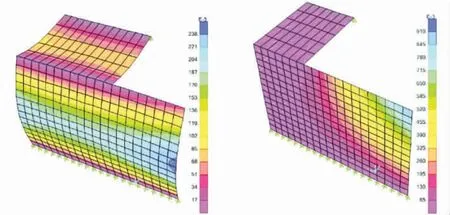
图5 剪力墙屈曲分析Fig.5 Buckling Analysis of Shear-wall
计算长度系数μ 随K 变化如图6所示。
从图6可以看出,计算长度系数μ 基本维持在1.0以下,能够满足规范限值要求,当线刚度比K=i板/i墙≥0.40 以上时,建议μ 取0.90;其余情况仍按规范限值取1.0 以便包络设计。
由图6的变化趋势线(虚线)所示,给出拟合公式:
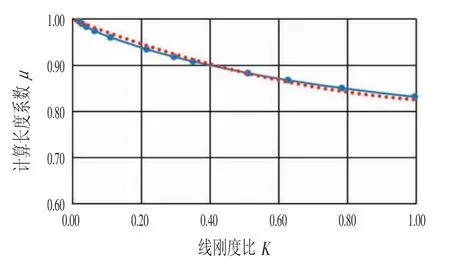
图6 计算长度系数μ随K变化图Fig.6 Effective Length Coefficient μ Changes with K
2.4 剪力墙开洞率对计算长度系数影响
SAP2000 计算模型参数同2.1 节带楼板模型,通过剪力墙开洞,即调整剪力墙开洞率γ 来分析计算长度系数μ 的变化情况。考虑到剪力墙洞口串联、并联的复杂性以及实际设计中的剪力墙开洞率,本文只讨论单个洞口,且开洞率γ<40%的情况。
剪力墙开洞模型如图7、图8所示。
计算长度系数μ 随γ 变化如图9所示。
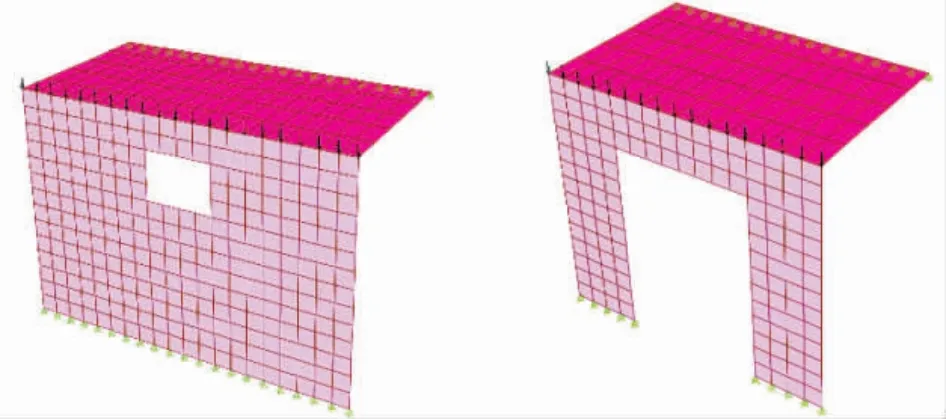
图7 剪力墙开洞示意Fig.7 The Hole Opening of Shear-wall

图8 剪力墙开洞屈曲分析Fig.8 Buckling Analysis of Shear Wall Opening
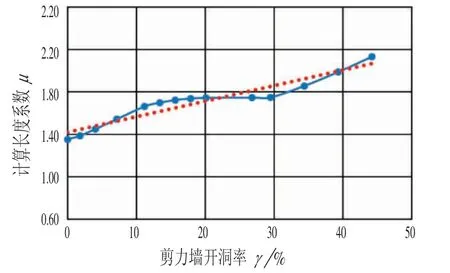
图9 计算长度系数μ随γ变化图Fig.9 Effective Length Coefficient μ Changes with γ
从图9可以看出,剪力墙开洞率对计算长度影响很大,在开洞率4%≤γ ≤30%时,计算长度系数μ 能够维持在1.2 以下,建议取1.2;在开洞率44%≥γ>30%时,计算长度系数μ 变化显著,峰值达到1.37,建议 μ 取 1.5。
由图9的变化趋势线(虚线)所示,给出拟合公式:
3 结论
本文通过调整楼板与墙肢长度比值,楼板与剪力墙线刚度比,剪力墙开洞率,定量分析了一字型剪力墙计算长度系数的变化,得出如下结论:
⑴楼板与墙肢长度比值不小于0.40 时,计算长度系数μ 基本能够满足规范值1.0 的要求;当比值小于0.40 时,计算长度系数呈线性急剧放大,实际设计中应尽量避免此情况。
⑵楼板与剪力墙线刚度比不大于0.40 时,计算长度系数取1.0;楼板与剪力墙线刚度比大于0.40 时,计算长度系数取1.0。
⑶剪力墙开洞率4%≤γ ≤30%时,建议计算长度系数取1.20;开洞率44%≥γ>30%时,建议计算长度系数取1.50。
根据楼板和剪力墙自身情况,给出了相应的计算长度系数拟合公式,提供工程参考。

