多方法融合的汽车质心侧偏角估计

高自群，谢桂芝，周兵，许艳，吴晓建，柴天

(1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；2.湖南大学 国家高效磨削工程技术研究中心，湖南 长沙 410082；3.南昌大学 先进制造学院，江西 南昌 330031)

随着人们对汽车安全需求的不断提升，越来越多的主动安全控制系统被应用于汽车[1-3]，质心侧偏角是稳定性控制系统的关键参数，能够及时准确地获取该参数对于汽车安全驾驶的意义重大.由于成本原因，商用车上很少通过如光学传感器、GNSS/INS 组合导航等检测装置直接获取质心侧偏角，而是采用软测量技术及状态观测的方式获取质心侧偏角[4].质心侧偏角观测器的构建方式主要分为3 种：1)基于运动学、2)基于动力学和3)基于运动几何.方式1）将传感器量测量(横摆角速度、侧向加速度、纵向速度)与质心侧偏角速度的微分关系式进行积分或者利用卡尔曼滤波算法得到质心侧偏角[5].方式1)对车辆参数的不确定性、路面附着条件以及驾驶操纵输入频率的变化具有鲁棒性，但对传感器的测量精度要求很高，对环境噪声、传感器偏置以及标定误差比较敏感[6].反馈补偿可以消除该方式中由传感器漂移、标定误差引起的量测信号偏差[7].方式2)是基于车辆动力学模型和轮胎模型进行观测器的构建，弊端在于估计结果的优劣依赖于观测模型以及模型参数(车辆参数、路面附着系数、过程噪声与量测噪声协方差矩阵等)的准确性.为了简化估计模型，建模时将如侧向风引起的横摆力矩与侧向力的因素忽略，由此导致估计结果的偏差[8-9].Zhang 等[10]提出自适应扩展卡尔曼滤波器，并将其用于克服过程噪声与环境噪声统计特性的不确定性对于估计精度的不利影响.为了更好地逼近非线性轮胎模型，提高观测器构建精度，Zhang 等[11]提出切换T-S 模糊观测器，估计车辆质心侧偏角.上述观测方法在一定程度上改善了方式2)的估计效果，但该方式的估计精度严重依赖于影响估计算法实时性的观测模型及参数的精确性.方式3）利用前、后轮侧偏角与质心侧偏角之间的运动几何关系进行质心侧偏角的估计[12]，特点是模型简单、计算量小、无积分操作，对于量测噪声、传感器偏置和部分车辆参数的不确定性具有一定的鲁棒性[13].方式3）所用运动几何关系式中的轮胎侧偏刚度取为定值，当轮胎侧向力处于线性阶段时，估计效果较好；当轮胎侧向力处于非线性阶段时，估计结果偏差较大[14].You 等[15]采用轮胎侧偏刚度辨识方法来适应轮胎侧偏刚度的非线性变化，该方法依赖路面附着系数的精确获取.单一的估计方式都存在不足，因此学者们开始尝试采用多方法融合估计方式.Nishio 等[16]将路面附着系数作为判断条件，以实现运动学与动力学估计方式的逻辑切换.相比动力学方式，运动几何方式结构更简单，计算量更小，对环境噪声、传感器偏置具有很好的鲁棒性[17].高博麟等[18]为运动学、动力学与运动几何方式分别设计子滤波器，使用主滤波器对子滤波器结果进行信息融合，得到全局融合结果.该方法所用的动力学子滤波器对轮胎模型进行简化，同时运动学子滤波器未考虑量测噪声统计特性的不确定性.Li 等[5]以动态特性的强弱为融合指标，对运动几何方式与运动学方式的估计结果进行择优融合；为了克服质心侧偏角的估计精度对于轮胎侧偏刚度精确性的依赖，利用PI 控制器对轮胎侧偏刚度进行实时反馈调节.该调整依赖于路面附着系数与轮胎模型的精确获取，Li 等[5]还将运动学估计方式的量测噪声统计特性(协方差矩阵R)预先设为定值，这与实际不符.

单一的估计方式向多方法融合估计方式的发展，一定程度上提高了质心侧偏角的估计精度，但融合估计的方式仍然待深入研究：1)尽管有学者利用PI 控制器对轮胎侧偏刚度进行了较准确的实时反馈调整，但该运动几何估计方式依赖于轮胎模型及路面附着系数等参数已知.2)量测噪声受环境影响较大，其统计特性具有不确定性.在融合估计过程中，量测噪声的统计特性根据先验值预先设为定值，但定值化处理不仅会降低估计精度，甚至会导致滤波发散.针对上述问题，本研究基于改进的质心侧偏角运动学与运动几何估计方法，设计质心侧偏角融合估计算法.

1 车辆模型

如图1 所示，传统线性二自由度无法描述车辆在非线性状态下的运动学关系，因此采用包含纵向、横摆与横向三自由度的车辆模型来表征车辆不同状态与参数之间的数学关系.图中， δf为前轮 转 角， αf， αr分 别 为 前、后 轮 侧 偏 角，Fyf、Fyr分别为前、后轮侧向力，Fxf、Fxr分别为前、后轮纵向 力，vy、vx分 别 为 侧 向、纵 向 速 度， ωr为 横 摆 角速度， β 为质心侧偏角，lf、lr为质心到前、后轴的距离，m为车辆质量，Iz为整车绕z轴转动惯量，整车平衡方程由纵向、侧向和横摆运动组成，描述如下.

图1 三自由度车辆模型Fig.1 Three degrees of freedom vehicle model

整车纵向运动：

整车侧向运动：

整车横摆运动：

为了后续观测器设计，将式(1)～(3)变形得到

前后轮的轮胎侧偏角描述为

考虑到纵向加速度对垂直载荷的影响，将垂直载荷描述为

式中：Fzf、Fzr分别为前、后轴垂直载荷，g为重力加速度，hg为质心高度.转向时横摆运动的产生伴随着左、右车轮速度的不一致，前轮转角也会影响车速与轮速之间的运动几何关系.

式中： ωi j为车轮角速度，r车轮半径，bf、br分别为前、后轮的轮距.

2 质心侧偏角融合观测器设计

2.1 质心侧偏角融合观测器整体结构

如图2 所示，质心侧偏角融合观测器分为4 个模块：1)自适应扩展卡尔曼滤波器(adaptive extended Kalman filter, AEKF)、2)运动几何观测器、3)融合权重计算、4)质心侧偏角融合估计值的计算.模块1）基于车辆纵、侧向速度，横摆角速度与纵、侧向加速度之间的运动学方程；构建具有量测噪声协方差R自适应调整功能的扩展卡尔曼观测器(EKF)；实现对车辆纵、侧向速度的估计.模块2）由侧向车速的代数计算式得到侧向车速估计值vy_m，利用模糊控制器对轮胎侧偏刚度进行实时校正，以提高侧向车速的估计精度.模块3）基于侧向车速融合结果的变化率v˙y_fuse提取瞬态特征值，再利用提取的瞬态特性值 S tbvy进行融合权重分配计算.模块4）依据融合权重，将模块1）、2）的侧向速度估计结果进行加权融合，得到侧向速度融合估计值vy_fuse，再结合AEKF 估计的纵向车速vx_k，计算得到车辆质心侧偏角的融合估计值 βfuse.融合观测器利用车载传感器获取的信息有车辆纵向速度vx_s，横摆角速度 ωr_s，车轮轮 速 ωi j，前轮 转 角δf以 及车 辆 纵、侧 向 加速 度ax_s、ay_s.

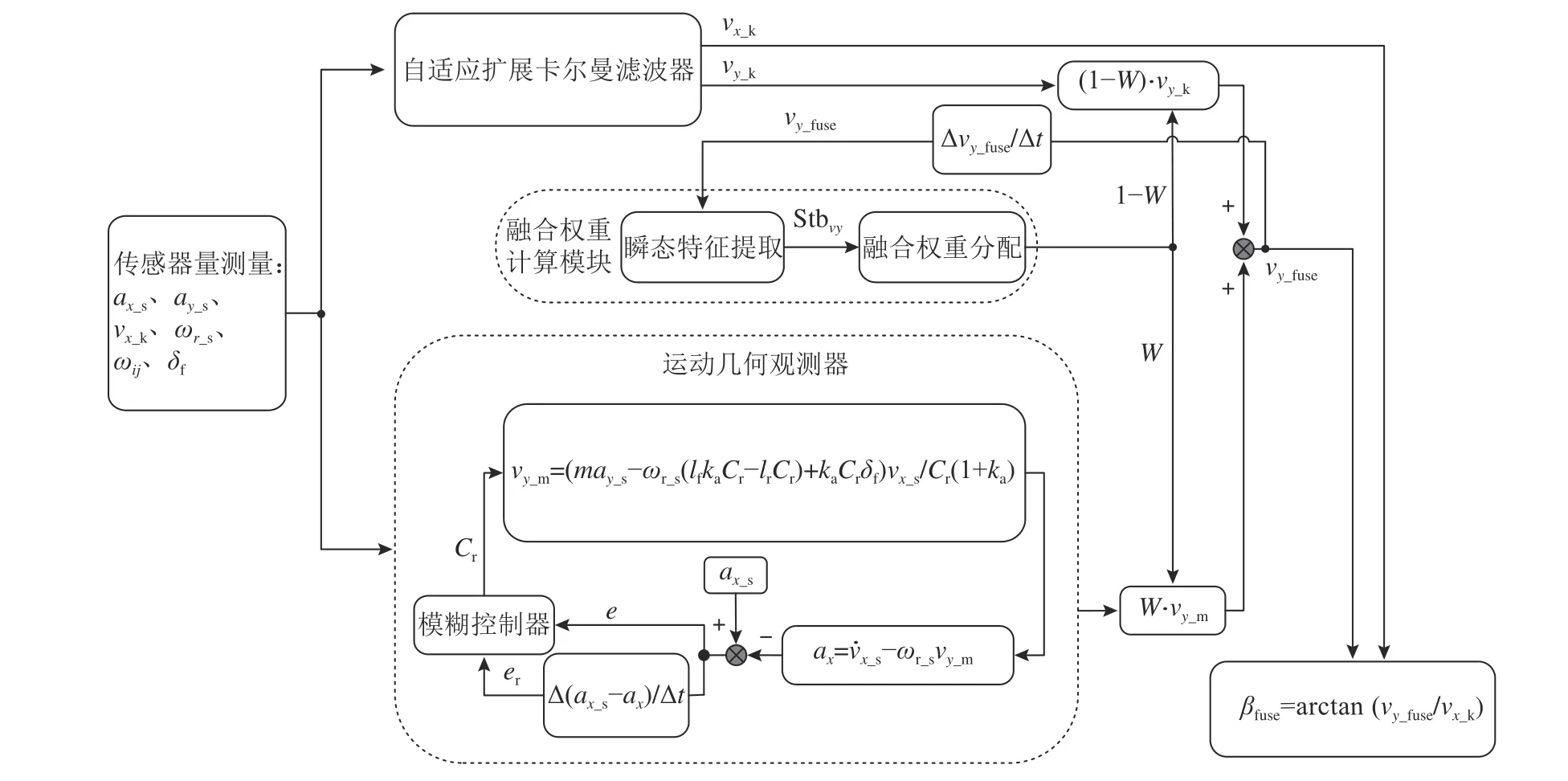
图2 质心侧偏角融合观测器结构图Fig.2 Structure diagram of sideslip angle fusion observer

2.2 自适应扩展卡尔曼滤波器的设计

化简式(4)、(5)得到车辆运动学方程v˙x=ax+ωrvy，v˙y=ay-ωrvx，选取量测方程为式(11)～(14)，依据状态估计流程，将运动学方程整理成状态方程和测量方程标准形式：

取采样时间为Ts=1 ms，离散化得到差分方程：

其 中Ak=I+A(t)Ts、Hk=H(t)，I为 与A(t) 同 维 的单位矩阵.

扩展卡尔曼滤波算法分为时间更新和量测更新2 个部分，算法流程如图3 所示.EKF 将量测协方差矩阵R视为定值，但在车辆实际行驶过程中，外界的环境噪声统计特性具有不确定性，将R视为定值会引起估计偏差.本研究在EKF 基础上加入量测协方差矩阵自适应算法，Zhang 等[10]指出新息能够很好地反应环境噪声对估计误差的影响，为此，可根据新息变化设计量测协方差矩阵自适应调整算法.定义新息 εk为量测量的实际值yk与预测值之间的误差：

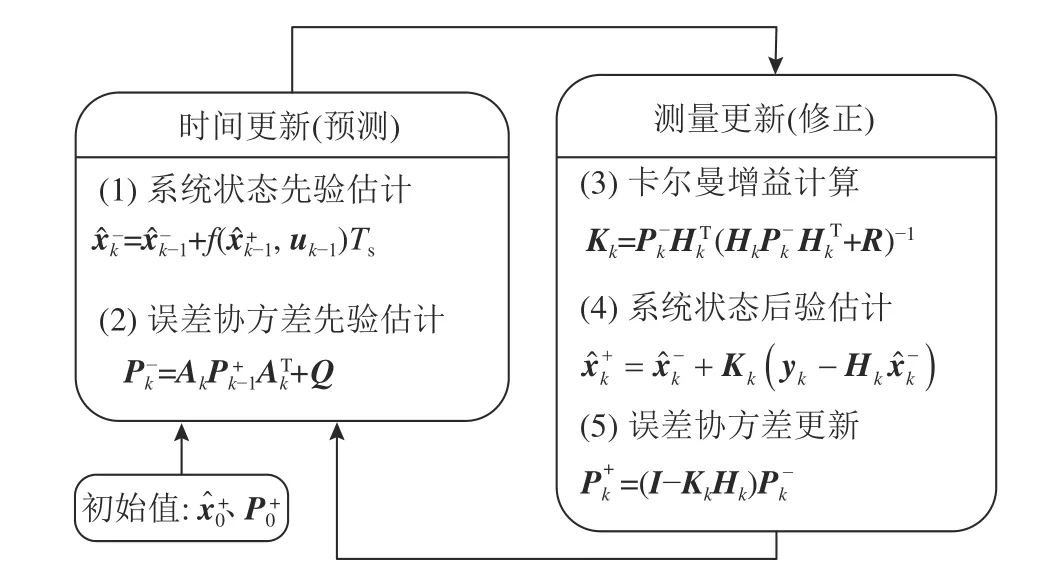
图3 扩展卡尔曼滤波算法流程图Fig.3 Flowchart of extended Kalman filter algorithm

新息的理论协方差矩阵

式中：E为期望值，为k时刻误差协方差矩阵先验值.新息的实际协方差矩阵

式中：M为滑动窗口的长度，取M=50.依据系统的实际新息协方差与理论协方差的相对大小，实时更新R，调整因子 αk的表达式[19]为

式中：tr() 为矩阵的迹，n为量测向量的维度.当Sk>Sˆk时，应 将R调 小，此 时 αk<1 ；当Sk≤Sˆk时，理论上应将R调大，考虑到将R值增大可能导致滤波发散，保持R不变，R=1.利用调整因子调整卡尔曼增益计算式：其中 αk可对R进行 自适应修正.

2.3 运动几何观测器设计

假设轮胎侧向力处于线性区域，则前、后轮胎侧向力分别为Fyf=Cfαf、Fyr=Crαr，其中Cf、Cr分别为前、后轮的侧偏刚度.定义Cf=kaCr，其中ka=Fzf/Fzr[14]，联合式(7)、(8)可以得到

由may_s=Fyf+Fyr、vx_s=vx、ωr_s=ωr，联立式(23)、(24)得到侧向速度代数计算式为

式中：ay_s、ωr_s、vx_s分别为传感器测得的侧向加速度、横摆角速度和纵向速度.式(25)只在推导过程中涉及轮胎力，实际应用时无需计算轮胎力.式(25)为代数计算式，无积分累计过程，即使量测信号存在偏差，估计结果也不会因累计误差而发散；式中除去可通过车载传感器与CAN 总线获取的状态量与输入量、整车质量m与质心到前后轴距离外，精确地获取轮胎侧偏刚度值是得到准确的侧向速度估计值vy_m的关键，在实际应用中，轮胎侧偏刚度受到垂直载荷、轮胎气压和路面附着条件等因素影响，难以获取精确的轮胎侧偏刚度值.如图4 所示为带有轮胎侧偏刚度自适应反馈调节的运动几何观测器.图中，侧向速度估计值vy_m通过式(25)计算得到，联合车辆侧向速度估计值、传感器测得的车辆纵向速度的变化率v˙x_s、横 摆 角速 度 ωr_s， 获取车 辆纵向 加速度 的计算 值ax，模糊控制器利用传感器测得的车辆纵向加速度ax_s与ax的差值e及其变化率er，对轮胎侧偏刚度进行实时反馈调节.该调节方式未涉及轮胎模型，因此对于路面附着系数变化具有鲁棒性.模糊控制器设计过程如下.1）确定模糊控制的输入与输出：当轮胎侧偏刚度越准确，纵向加速度量测值ax_s与理论计算值ax之差越接近零；反之，其绝对值将越大.将e、er作为模糊控制的输入，以后轮胎侧偏刚度Cr作为模糊控制的输出.2）定义模糊控制的输入输出模糊集：NVB、NB、NVM、NM、NVS、NS、Z、PS、PM、PB 分别表示负很大、负大、负很中、负中、负很小、负小、零、正小、正中、正大.3）定义输入输出的隶属度函数Df，如图5 所示.4）通过大量的仿真试验与理论分析，积累足够的专家经验后，制定如表1 所示的模糊规则.利用Matlab 的模糊逻辑工具箱生成Simulink 中模糊控制器模块的可执行文件，其中模糊控制器的解模糊化方法为重心法.

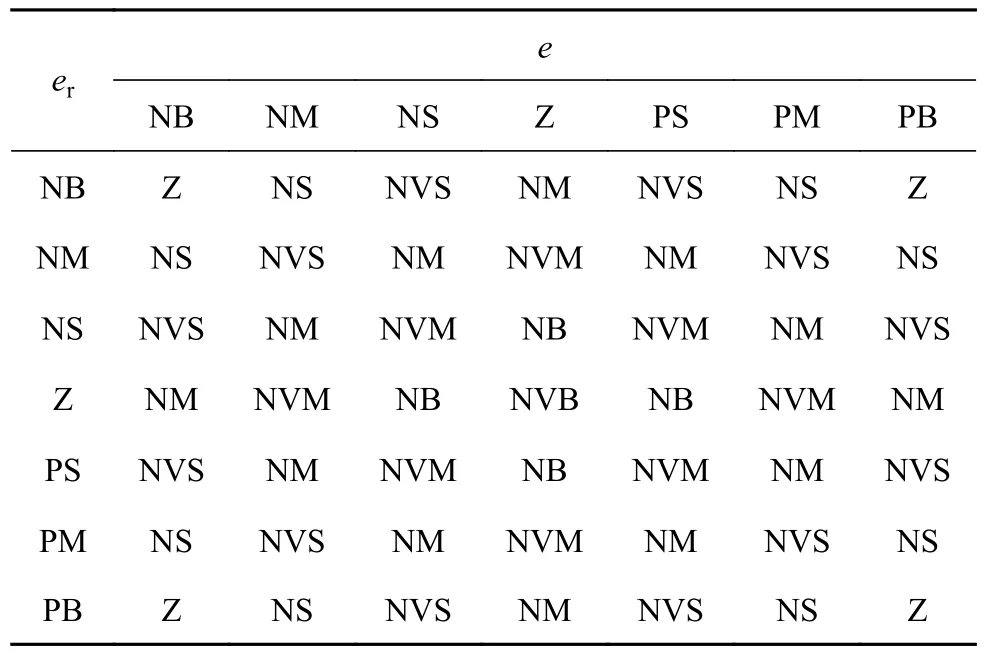
表1 后轮胎侧偏刚度的模糊规则Tab.1 Fuzzy rule of rear tyre lateral stiffness

图4 运动几何观测器流程图Fig.4 Flowchart of kinematic-geometric observer

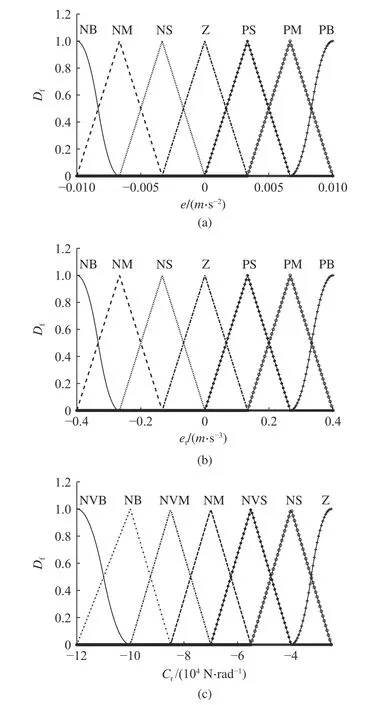
图5 隶属度函数Fig.5 Membership function

2.4 2 种估计方式的对比分析

运动学方式在方向盘处于机动状态(车辆状态的变化率较大)时有较好的估计效果[20]，为了分析所提运动几何估计方式在不同车辆状态变化率下的具体表现，参考Li 等[5]探究不同估计方式适用范围的试验方案，设置阶跃-回正试验进行仿真分析.

如图6 所示为在vx=90 km/h，路面附着系数µ=0.85条件下，阶跃-回正仿真试验结果对比图.称图6(b)中侧向速度变化率较大的填充区域为瞬态区域，该区域车辆侧向速度变化较剧烈；根据有无转向输入，将剩余侧向速度变化率v˙y较小的区域分别称为非零、零稳态区域.依据图6 分析2 种估计方式的特点：在瞬态区域t=4～7 s 和t=15～17 s，运动学方式相比于运动几何方式具有更好的实时跟随估计效果；在非零稳态区域t=7～15 s，运动学方式由于积分累计误差的影响，估计偏差呈现逐渐增大的趋势，运动几何方式的估计结果虽存在一定偏差，但偏差值相对较小，且并未随时间增大；在方向盘回正后的零稳态区域t=17～20 s，运动学方式的估计结果依然存在偏差，运动几何方式的估计偏差接近于零.经上述分析可知，运动学方式在瞬态区域估计效果相对较好，运动几何方式在零、非零稳态区域内有可接受的估计精度.

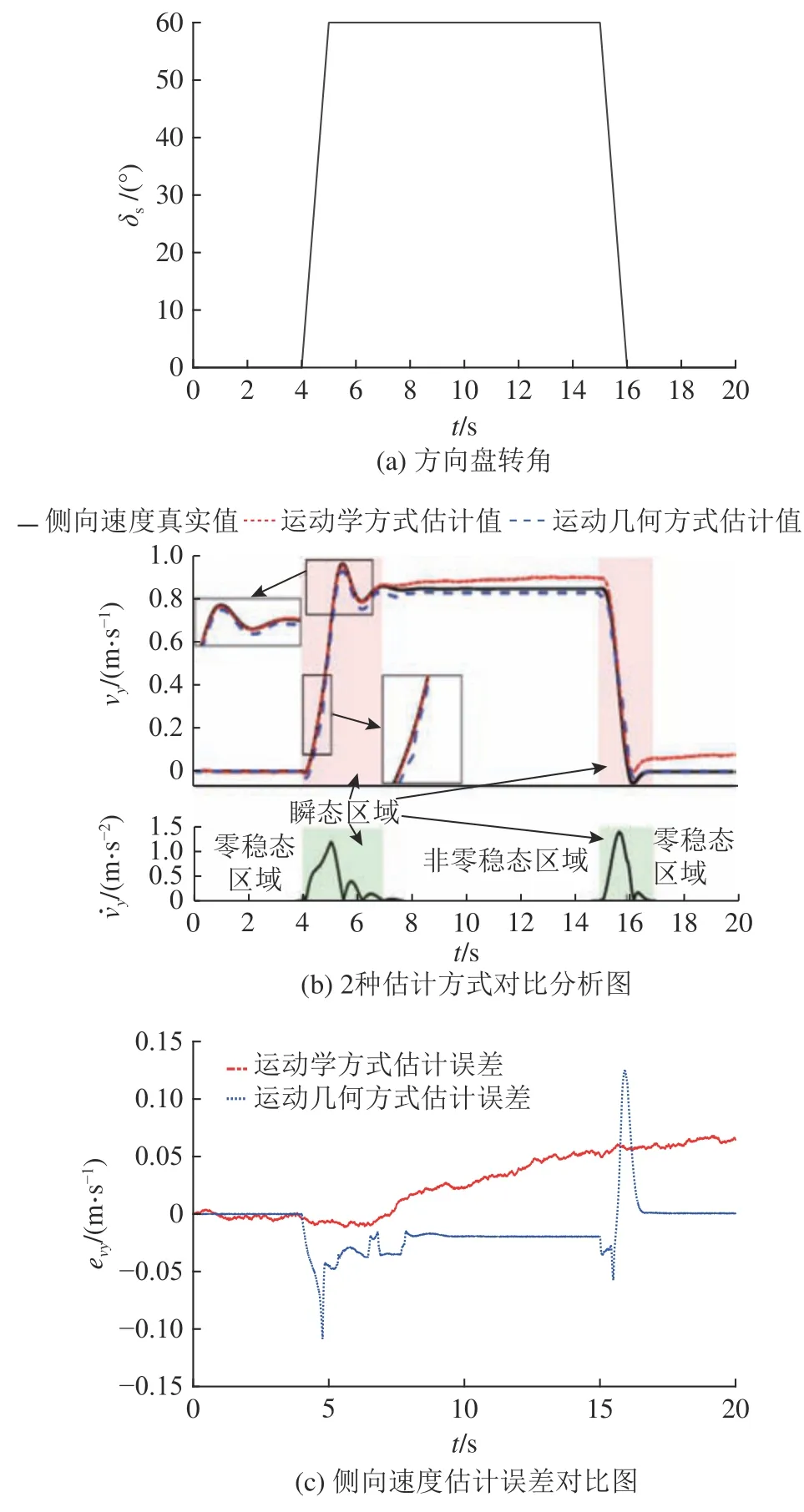
图6 运动学与运动几何方式的估计结果对比Fig.6 Comparison of estimation results between kinematic method and kinematic-geometry method

2.5 融合估计算法设计与验证

2.5.1 融合估计算法设计 本研究提出以状态量的瞬态特性强弱（用于表征状态量变化率的大小）为融合指标的融合算法，该算法的流程图如图7 所示.Cheli 等[20]将侧向加速度、横摆角速度和方向盘转角在0～0.1 s 的均方根加权之和作为衡量状态量稳态特性强弱的指标，用于融合算法的设计.借鉴该思想，将侧向速度变化率v˙y_fuse作为瞬态特性指标的提取对象.图中缓存器输出当前时刻前推0.1 s 的侧向速度变化率，接着利用侧向速度变化率进行均方根计算，计算结果通过一阶低通滤波器去除噪声，得到瞬态特性指标值Stbvy.将S tbvy输入融合权重计算模块，该模块利用Stbvy与前轮转角 δf进行融合权重的分配计算.融合权重计算式为

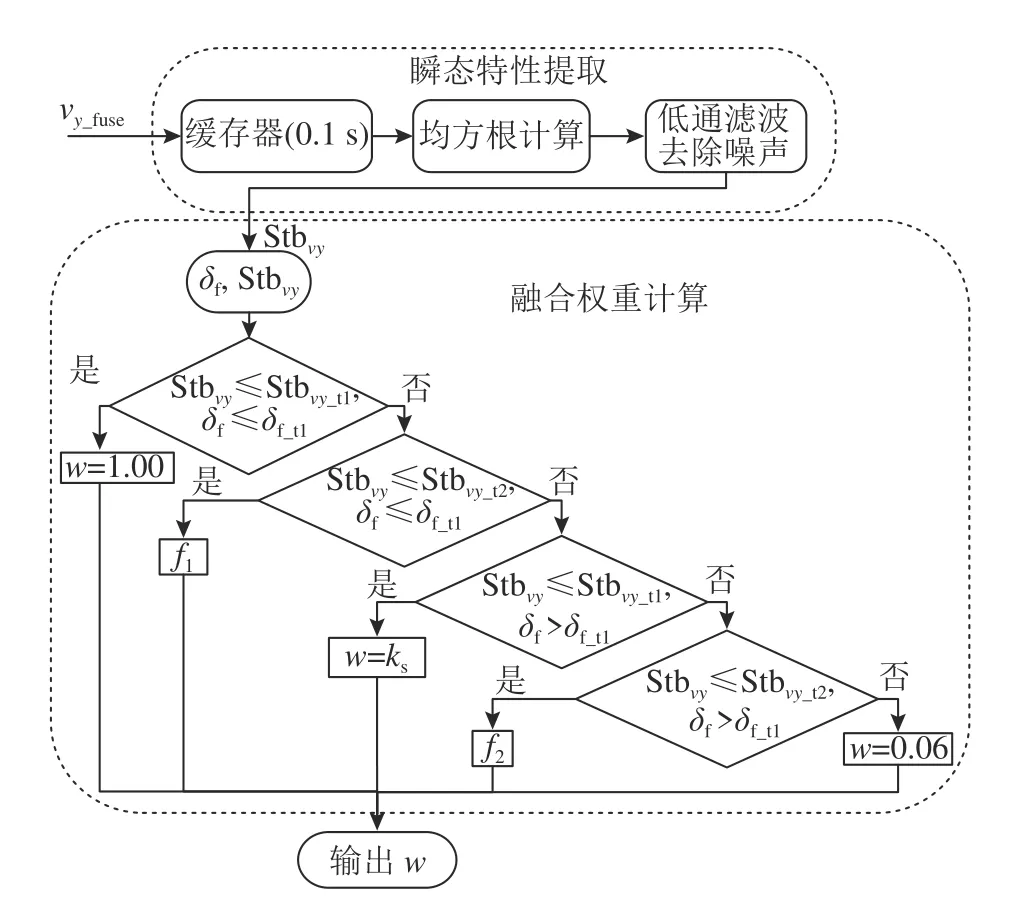
图7 融合算法流程Fig.7 Fusion algorithm process

1) 当 S tbvy小 于 阈 值 S tbvy_t1， δf小 于 阈 值 δf_t1时，车辆状态处于零稳态区域，依据2.4 节的结论，该区域运动几何方式的估计结果偏差接近于零，因此，给与运动几何方式的融合权重w=1.00.2)当Stbvy小 于 阈 值 S tbvy_t2时，如 果 δf小 于 阈 值 δf_t1，融合权重依据式(27)计算，该区域为瞬态与零稳态区 域 的 过 渡 区 间.如 果 δf大 于 阈 值 δf_t1，融 合 权 重依据式(28)计算，该区域为瞬态与非零稳态区域的过渡区间.设置过渡区间可避免融合权重的突变导致融合估计结果的突变.3)当 S tbvy小于设定的 阈 值 S tbvy_t1， δf大 于 设 定 的 阈 值 δf_t1，表 明 车 辆状态处于非零稳态区域，以运动几何方式的估计结果为主，融合权重为ks(依据运动几何方式稳态偏差大小而定)，本研究取0.75.4)当 S tbvy大于设定的阈值 S tbvy_t2，此时车辆状态处于瞬态区域，以运动学方式的估计结果为主，融合权重w=0.06.

2.5.2 融合估计算法验证 阶跃-回正试验进行融合算法的验证，取 S tbvy_t1=0.01, Stbvy_t2=0.1, δf_t1=0.3°，ks=0.75.如图8 所示为融合权重分配结果图.在零稳态区域(t=0～4 s、t=17～20 s)与非零稳态区域(t=7～15 s)，瞬态特性值 S tbvy较小，运动几何法的权重为1；瞬态特性值 S tbvy高 的区域(t=4～7 s、t=15～17 s)运动几何的融合权重为0.06，不同区域之间的融合权重也能平滑过渡；输出的融合权重能依据瞬态特性值大小进行动态变化，符合设计要求.

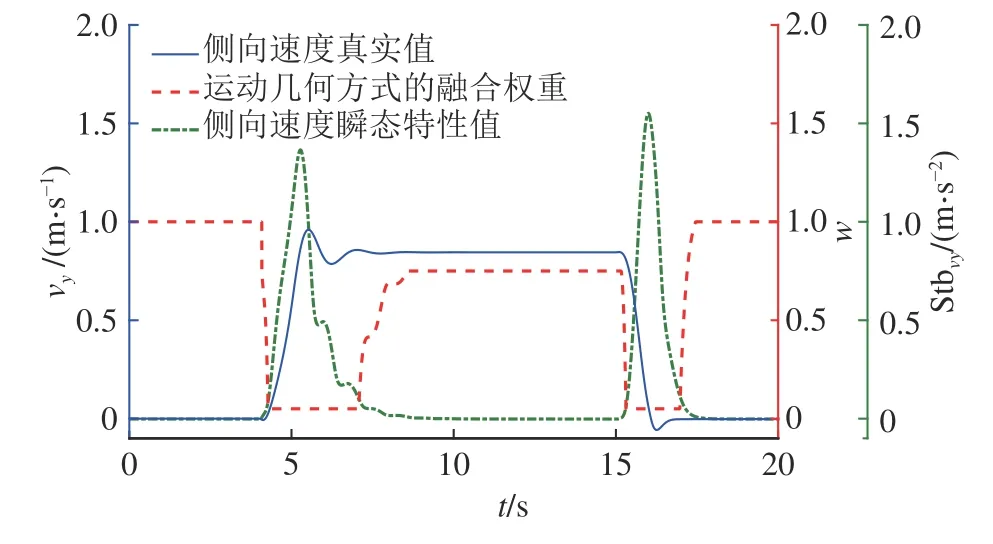
图8 融合权重分配图Fig.8 Fusion weight distribution chart

3 仿真验证

采用Carsim-Simulink 的仿真与驾驶员在环(DIL)试验平台，以Carsim 输出的值为参考值，验证本研究提出的融合观测器的有效性，整车参数如表2 所示.模拟真实的传感器量测信号，须为Carsim 的理想输出添加合适的零均值高斯白噪声，各量测输入所加噪声的方差[21]取值如下：Varωi j= 0.002 rad/s、Varax= 0.001 m/s2、Varay= 0.002 m/s2、Varωr= 0.004 rad/s、 V arvx= 0.001m/s.设计角阶跃、双移线、变附着系数对接路面-双移线等仿真工况以及驾驶员在环试验，对所提融合观测器的估计准确性进行验证.为了体现矩阵R自适应对于运动学方式估计精度的提高效果，仿真结果对有无矩阵R自适应的运动学方式进行比较.为了定量分析估计误差，选用均方根误差作为评价指标：

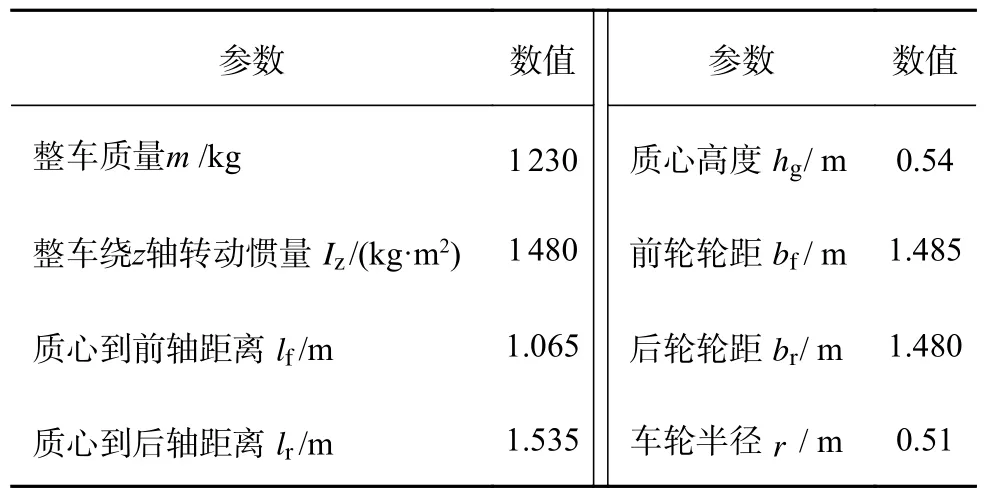
表2 Carsim 车辆参数Tab.2 Parameters of Carsim vehicle

式中： βi、^βi为质心侧偏角的真实值和估计值.

1) 双移线、角阶跃工况.初始车速vx= 100 km/h，µ=0.85，仿真时间t=10 s，方向盘转角如图9 所示.依据仿真结果图10 和表3 可知，有自适应相比于无自适应的运动学方式，双移线工况、角阶跃工况的估计结果的均方根误差值分别减少了37%、51%；融合方式相比于自适应运动学方式与运动几何方式，估计结果的均方根误差值在双移线工况中分别减少了24%、58%，在角阶跃工况中分别减少了56%、38%.因此加入自适应可提高运动学方式的估计精度，与此同时，融合运动学方式（自适应）与运动几何方式的估计结果可进一步提高估计精度.

表3 2 种工况估计结果的均方根误差Tab.3 Root mean squared error of estimation results under two conditions

图9 2 种工况的方向盘转角Fig.9 Steering angles of two conditions

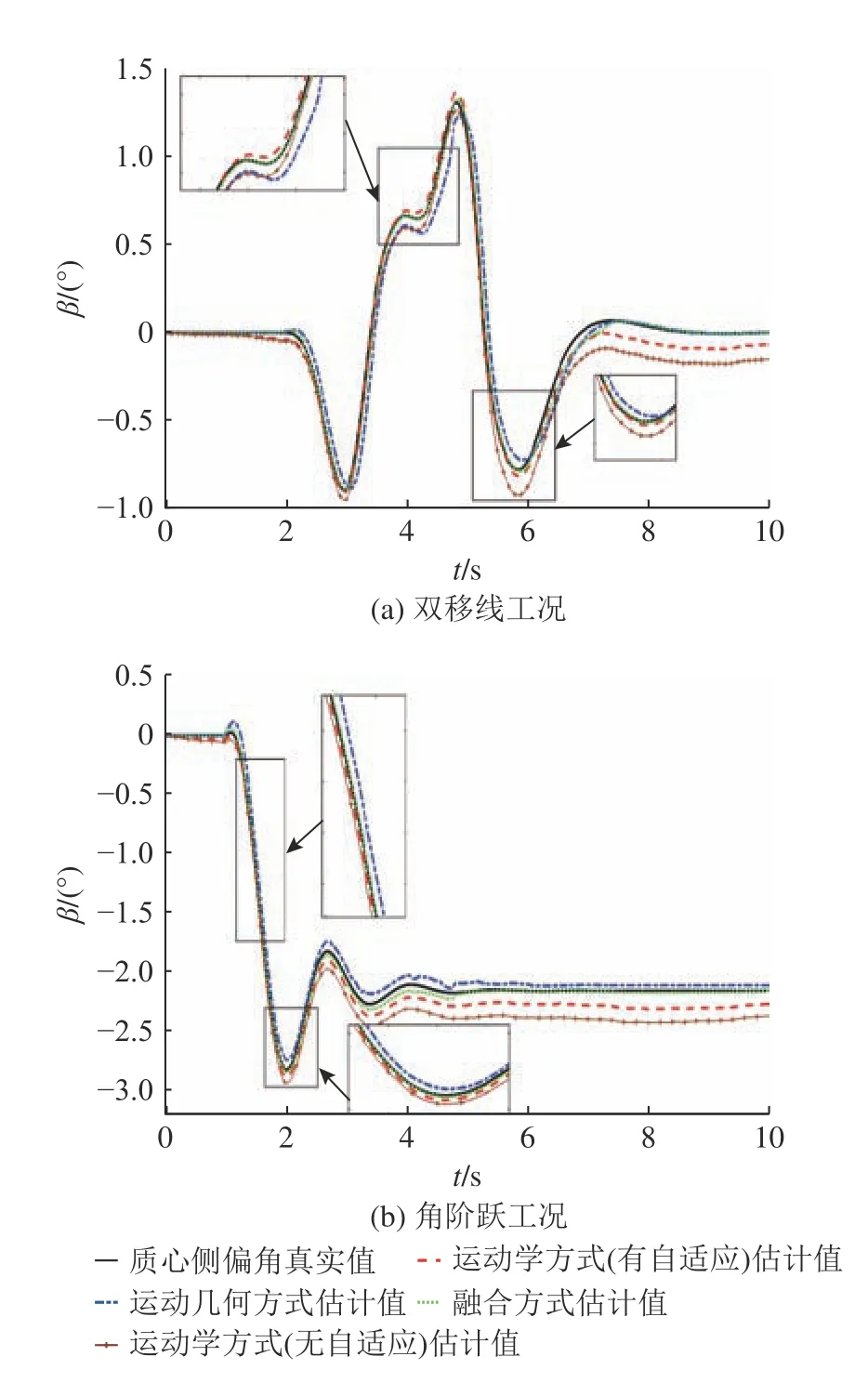
图10 2 种工况的质心侧偏角估计结果Fig.10 Results of sideslip angle estimation for two conditions

2) 变路面附着系数对接路面-双移线工况.为了验证所提观测器对路面附着系数变化的鲁棒性，选取文献[5]中提出的融合估计方式作为类比对象，记为融合方式B，该方式的估计精度依赖于路面附着系数的准确性.所提观测器记为融合方式A.利用变路面附着系数对接路面-双移线工况进行验证，在Carsim 中设置长直道，纵向0～300 m路面附着系数 µ=0.85 ，300～600 m 路面附着系数µ=0.5， 横向方向路面附着系数一致.车速vx= 90 km/h，方向盘转角如图11(a)，仿真时间t=25 s，仿真结果如图11(b)所示，融合方式A、B 估计结果的均方根误差分别为0.033、0.126.当t=0～15 s，融合方式A 的估计精度略高于融合方式B；t> 15 s，路面附着系数由0.85 突变到0.50，融合方式A 依然能够得到较好的估计结果；由于算法中的路面附着系数不能及时更新为0.5，融合方法B 的估计精度明显降低，融合方法B 总体估计结果的均方根误差值相比于融合方法A 增加了73%.

3) DIL 试验.为了进一步验证所提观测器的有效性与实时性，开展DIL，如图12 所示为DIL仿 真 平 台.初 始 车 速vx= 90 km/h ， µ =0.85 ，分 别 进行双移线、角阶跃试验，试验结果如图13 所示，均方根误差如表4 所示.相比于自适应运动学估计方式与运动几何方式，本研究所提融合估计方式的均方差误差值均有所减少，双移线试验中分别减少了34%、56%，角阶跃试验中分别减少了61%、47%.在试验所用美国国家仪器(national instruments, NI)机箱的数据输出频率为1 000 Hz，即时间间隔为1 ms，观测器每一步仿真平均用时(simulation time)分别为350、321 μs ，均小于设置的仿真步长，实时性满足要求.

图12 驾驶员在环仿真平台Fig.12 Driver in loop simulation platform

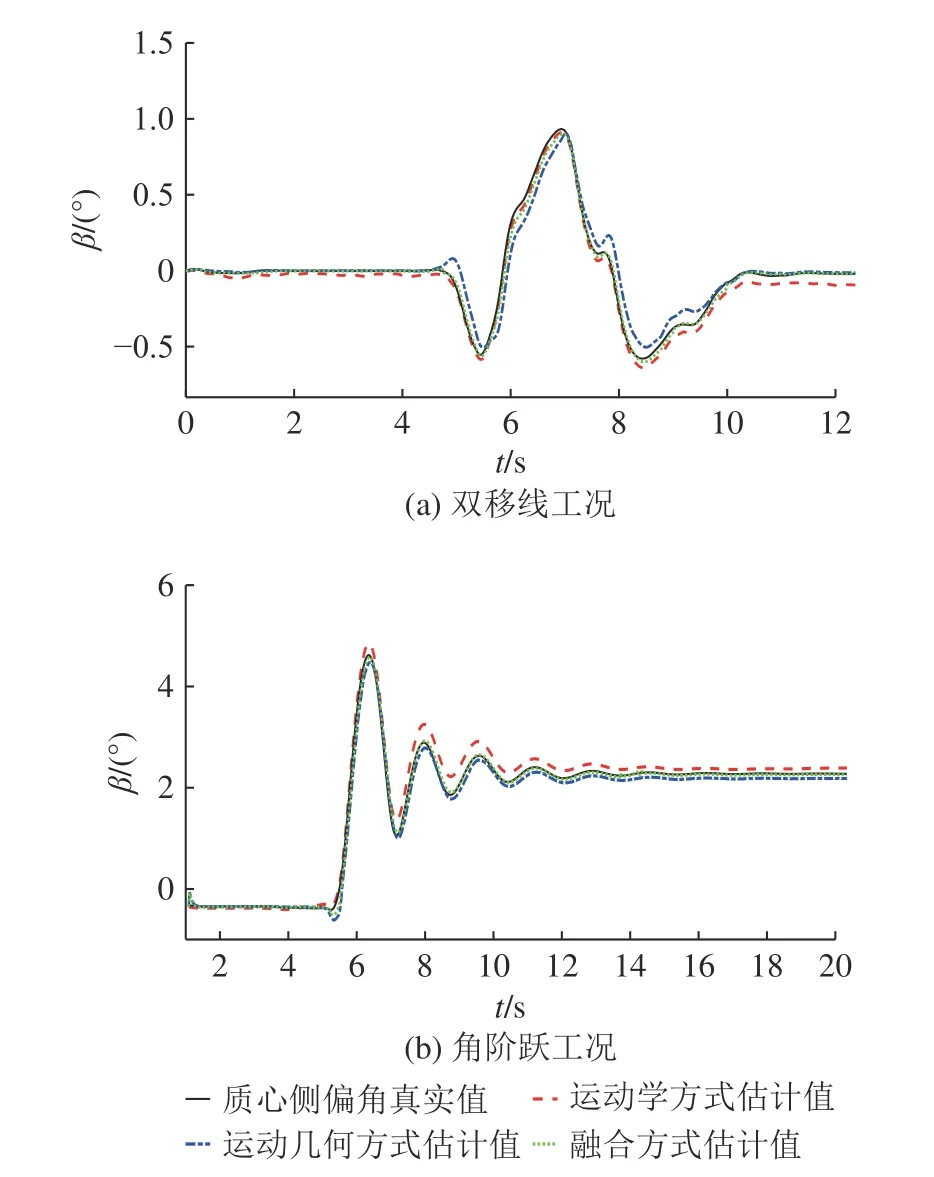
图13 2 种工况的驾驶员在环试验质心侧偏角估计结果Fig.13 Results of sideslip angle estimation of two conditions for driver in loop simulation test

4 结 语

设计可实现量测噪声协方差矩阵自适应以及轮胎侧偏刚度模糊自适应的质心侧偏角融合估计算法.在Carsim-Simulink 的仿真与驾驶员在环仿真平台展开的多工况试验结果显示，本研究设计的质心侧偏角融合观测器可实时获取较准确的质心侧偏角估计结果，即使在路面附着系数突变条件下，也能实现较准确估计.所提融合估计算法的验证仅在Carsim-Simulink 以及驾驶员在环仿真平台进行，后续考虑进行实车试验，对所提算法做进一步验证.