基于改进哈里斯鹰算法的梯级泵站优化调度

张雷克，侯笑鹏，刘小莲，田雨

(1.太原理工大学 水利科学与工程学院，山西 太原 030024；2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038)

为了有效解决地区水资源短缺，加强农业灌溉，保障城市供水，促进社会、经济与生态协调发展，人们建成了众多由梯级泵站组成的大型跨流域调水工程[1-2].梯级泵站在运行过程中往往存在运行效率低、耗电量大的问题[3-4].开展梯级泵站运行调度优化研究，最大限度提高系统运行效率、节省用电成本，对提升泵站综合利用效率、优化经济运行方式及增强运行管理水平具有十分重要的科学意义和工程应用价值.

梯级泵站系统优化调度是复杂的非凸、非线性、高维优化问题，传统的优化方法往往计算复杂或难以得到最优解.作为优化方法的一大分支，群智能算法的出现为传统优化方法的求解提供了有益的补充[5].鉴于它高效、简单、易于实现等优点，众多启发式智能算法，如遗传算法（genetic algorithm, GA）、蚁群算法（ant colony optimization,ACO）、模拟退火（simulated annealing, SA）、粒子群算法（particle swarm optimization, PSO）、狼群算法（wolf pack algorithm, WPA）等都被用来解决复杂优化调度问题[6-11].每种算法各有其优缺点[12]：GA 适用范围较广，可有效求解复杂优化问题，但该算法控制变量较多，收敛速度较慢；PSO 寻优速度较快，适用范围广，能够高效求解连续函数的优化问题，但存在局部寻优能力较差的缺点；ACO 与SA 的鲁棒性强，但二者均对参数较为敏感.为了更高效地获取梯级泵站优化调度问题最优解，新算法的提出与已有算法的改进成为本领域关注重点.哈里斯鹰算法（Harris hawks optimization algorithm，HHO）[13]是新型仿生智能优化算法.在自然界中，哈里斯鹰会利用犀利的双眼侦察环境，并在追踪、围攻和攻击阶段高效地执行协作觅食[14].HHO 可根据猎物逃逸能量选取不同的围攻策略使哈里斯鹰个体沿不同方向搜索，算法中的Levy 飞行策略提供了步长符合Levy 分布的随机游走方法，增强了算法随机性及对全局最优值的搜索能力.由于HHO 具有参数少、鲁棒性强的优点，算法解决多约束复杂优化问题的效果良好，被广泛应用于电力、机械及水利优化调度等领域[15-22].在水利工程方面，径流预测是流域水资源合理配置的重要依据，为了提高预测精度及性能，Sun 等[21]建立基于改进HHO 的短期径流预测模型，通过与其他模型进行比较，验证了改进算法的有效性及优越性.Liu 等[22]提出动态多群差分学习HHO，并将它应用于梯级水电站优化调度问题，通过与其他算法比较，证明了提出算法良好的实用性.

HHO 在水利水电优化调度领域的良好表现已被证实，且该算法的高收敛精度与收敛速度对梯级泵站系统运行效率提升具有较大潜力，但HHO 尚未被应用于解决梯级泵站优化调度问题.针对算法探索与开发之间不平衡、算法易陷入局部最优的问题[23-25]，本研究通过引入饥饿率与偏移项优化策略提出改进哈里斯鹰算法（improved Harris hawks optimization algorithm, HUHHO），以进一步提高HHO 的收敛精度与收敛速度.本研究以梯级泵站运行效率最大化为目标，建立梯级泵站优化调度模型，提出基于HUHHO 的梯级泵站优化调度方法，并将该方法应用于北京市某三级泵站优化调度问题中.通过与现状方案和基于PSO、GA 及HHO 的优化方案对比，验证HUHHO 在梯级泵站优化调度中的有效性及优越性.

1 梯级泵站优化调度模型

梯级泵站调水工程的能量消耗多集中于稳态运行期间，主要受各级泵站内流量分配和泵站间扬程分配的影响.将水库、输水渠道和泵站等作为整体，在满足各种稳态等式和不等式约束的情况下，以梯级泵站运行效率最大化为目标，建立梯级泵站优化调度模型[26].由于梯级泵站优化调度问题属于大系统优化问题，常采用分解协调模型求解，故将该系统分解为单级泵站流量优化模型和梯级泵站扬程优化模型2 个子系统.通过优化算法，先实现各子系统的最优化，再考虑各子系统间的关联，实现大系统的全局最优化.系统分解协调模型如图1 所示.由单级泵站流量优化模型可以得到各泵站机组间最优流量分配组合，使各泵站运行效率最大、运行费用最小；梯级泵站扬程优化模型在考虑水头损失的基础上可以得到总扬程在梯级泵站之间的最优分布[27]，使得梯级泵站总效率最大；水力损失由一维水力模拟模型计算得到.

图1 梯级泵站优化调度模型结构图Fig.1 Structure diagram of optimal dispatching model for cascade pumping station

1.1 一维水力模拟模型

一维水力模拟模型被广泛应用于水库调度、梯级泵站系统优化等工程领域，本研究采用圣维南方程组构建一维水力模拟模型，对实际工程中一些复杂的内部构筑物如泵站、倒虹吸和渐变段等进行概化处理，耦合概化后的构筑物模型与圣维南方程组.采用Preissmann 四点时空偏心格式对方程组进行离散，借助双扫描法求解离散方程组[27].利用所构建的一维水力模拟模型可以通过计算得到各流量和水位组合下梯级泵站调水工程各渠段的水头损失.

1.2 单级泵站流量优化模型

单级泵站流量优化问题实质上是流量负荷在泵站机组之间分配的空间最优化问题，即在调水流量、工作扬程一定的情况下，以满足流量平衡、水泵运行性能约束为前提，合理确定开机台数、优化机组间流量分配，以使泵站效率最大的过程.

1.2.1 目标函数 以包含n台水泵的第j级泵站为例，其运行效率最大化的目标函数为

式中：ηj,max为第j级泵站在总流量Qt和扬程Hj条件下的最大效率；Qj,k、ηj,k分别为第j级泵站中第k台机组的流量和效率.

1.2.2 约束条件 1）流量平衡为

2）单泵流量约束为

式中：Qj,k(min)、Qj,k(max)分别为第j级泵站中第k台单泵的允许最小和最大流量.

1.3 梯级泵站扬程优化模型

梯级泵站扬程优化问题实质上是总扬程在梯级泵站之间分配的空间最优化问题，即在满足各渠段水力联系、各级泵站进水和出水池水位约束等前提下，优化扬程在梯级泵站间的分配，使梯级泵站总效率最大.

1.3.1 目标函数 梯级泵站的总效率计算式为

式中：Ht为梯级泵站的总水头；b为梯级泵站总级数.

1.3.2 约束条件 1）水力平衡约束为

式中：Zout,b为第b级泵站出水池的水位；Zin,1为第一级泵站进水池水位；hj,j+1为第j级泵站和第j+1 级泵站之间渠道的水力损失.

2）单级泵站水头约束为

式中：Hj,min、Hj,max分别为第j级泵站的允许最小和最大水头.

3）泵站出水池水位约束为

式中：Zout,j(min)、Zout,j(max)分别为第j级泵站出水池允许最低及最高运行水位.

4）泵站前池水位约束为

式中：Zin,j(min)、Zin,j(max)分别为第j级泵站进水池允许最低、最高运行水位.

2 改进哈里斯鹰算法

2.1 哈里斯鹰算法

HHO 种群个体的更新主要由探索、探索到开发的转换和开发阶段组成.

2.1.1 探索阶段 哈里斯鹰随机栖息在某些位置，并基于2 种策略搜寻猎物，公式为

式中：Xi(t)、Xi(t+1)分别为第t代、第t+1 代种群中第i个体；Xr(t) 为从第t代种群中随机选取的个体；Xrab(t)为猎物位置，即截止到第t代所得的全局最优个体；r1、r2、r3、r4、q均是(0，1)的随机数；u、l表示个体的上、下界；Xm(t)为第t代种群所有个体平均位置，

式中：N为种群规模.

2.1.2 探索到开发的转换阶段 HHO 的探索阶段向开发阶段转换由猎物的逃逸能量E控制，

式中：E0为猎物的初始逃逸能量，取值为（-1，1）的随机数；T为最大迭代次数.当|E|≥1 时进入探索阶段，|E|＜1 时进入开发阶段.

2.1.3 开发阶段 算法的开发阶段包括4 种不同的搜索策略：软围困、硬围困、渐进式快速俯冲硬围困和渐进式快速俯冲软围困策略，用以模仿鹰群捕食猎物的过程.根据逃逸能量及区间（0，1）上的随机数r的取值执行相应的种群更新.

1）软围困：当|E|≥0.5，r≥0.5 时，猎物仍有足够的体力去逃脱，鹰群将会轻轻地环绕追逐猎物，使猎物疲劳.该策略表达式为

式中：ΔXi(t)为猎物位置与哈里斯鹰当前位置之间的向量差；J为猎物在逃跑过程中的随机跳跃强度，J=2（1-r5），其中r5为（0，1）上的随机数.

2）硬围攻：当|E|＜0.5，r≥ 0.5 时，猎物的体能较低已不足以逃脱追捕.该阶段的表达式为

3）渐进式快速俯冲软围困：当|E|≥0.5，r<0.5时，猎物仍有能量去逃跑，鹰群将会产生环绕软包围追捕猎物.此阶段的更新表达式为

式中：f（·）为最小化问题的目标函数值，Y1、Z1分别为

式中：D为问题的维数；S为大小为1×D的（0，1）上的随机向量；LF 是Levy 飞行函数，计算式为

式中：u、v均为（0，1）的随机数；β 为默认常数，设置β=1.5.

4）渐进式快速俯冲硬围困：当|E|<0.5，r<0.5 时，猎物没有足够的能量逃跑，鹰群构建环绕硬围困来捕获猎物.该策略的表达式为

2.2 改进哈里斯鹰算法

HUHHO 的改进策略能够解决HHO 探索与开发之间不平衡、算法易陷入局部最优的问题，提升HHO 的收敛精度与收敛速度.1）受非洲秃鹫算法[28]（African vultures optimization algorithm，AVOA）启发，在哈里斯鹰探索到开发的转换阶段引入饥饿率，以反映哈里斯鹰饥饿程度，从而更好地实现探索与开发之间的平衡；2）在探索阶段添加1 个偏移项，以考虑哈里斯鹰饥饿感强弱对搜寻猎物能力的影响，提高算法的寻优能力、避免陷入局部最优.

2.2.1 饥饿率 高频次对食物的搜寻是哈里斯鹰的生活常态.若哈里斯鹰处于饱腹状态，足够的能量能够确保它飞行更远距离寻找猎物；若摄入食物不足，则无法拥有充足能量保证长时间飞行.上述行为的描述，文献[28]已有所体现，且已证实考虑搜寻者的饥饿程度可以增强算法解决复杂优化问题的性能，提高从局部最优点逃逸的可靠性[29]，相关表达式为

式中：F为饥饿率，其值越大，代表哈里斯鹰饥饿程度越弱；h为（-2，2）的随机数；ω 为固定参数，取ω=2.5；f为扰动项，受当前迭代次数t影响；rand1为随机值，在（0，1）取值；z为（-1，1）的随机数，会随着迭代次数的变化而变化.当z<0 时，表示鹰饥饿，z>0，表示鹰饱腹.当|F|>1 时，鹰会在不同的区域寻找食物，即为全局探索阶段.如果|F|<1，进入开发阶段，鹰会就近搜寻食物.

2.2.2 偏移项 哈里斯鹰在捕捉猎物时不同程度的饥饿感会造成相应程度的意识模糊，进而导致其栖息位置较原位置发生一定偏移.为了模拟上述行为，在式（10）中增添大小为1×D的偏移项D'.向量D'中每项均为10qF，即D'=[10qF，···，10qF]，以此来体现饥饿对哈里斯鹰全局探索的影响.改进后的种群探索阶段更新公式为

式中：若q≥0.5，鹰随机栖息，且栖息位置相较于原位置进行了矫正.当q<0.5 时，哈里斯鹰意识较为清醒，注意力集中，更容易找到猎物位置Xrab，且偏移距离|D'|相对较小.在局部开发阶段未引入偏移项的原因：当|F|<1 时，哈里斯鹰只能在小范围内搜寻猎物，饥饿感造成的偏移位置较小，可以忽略.仍采用类似HHO 的局部搜索策略，仅将式（13）～（22）中的逃逸能量用饥饿率替代.HUHHO的算法流程如图2 所示.

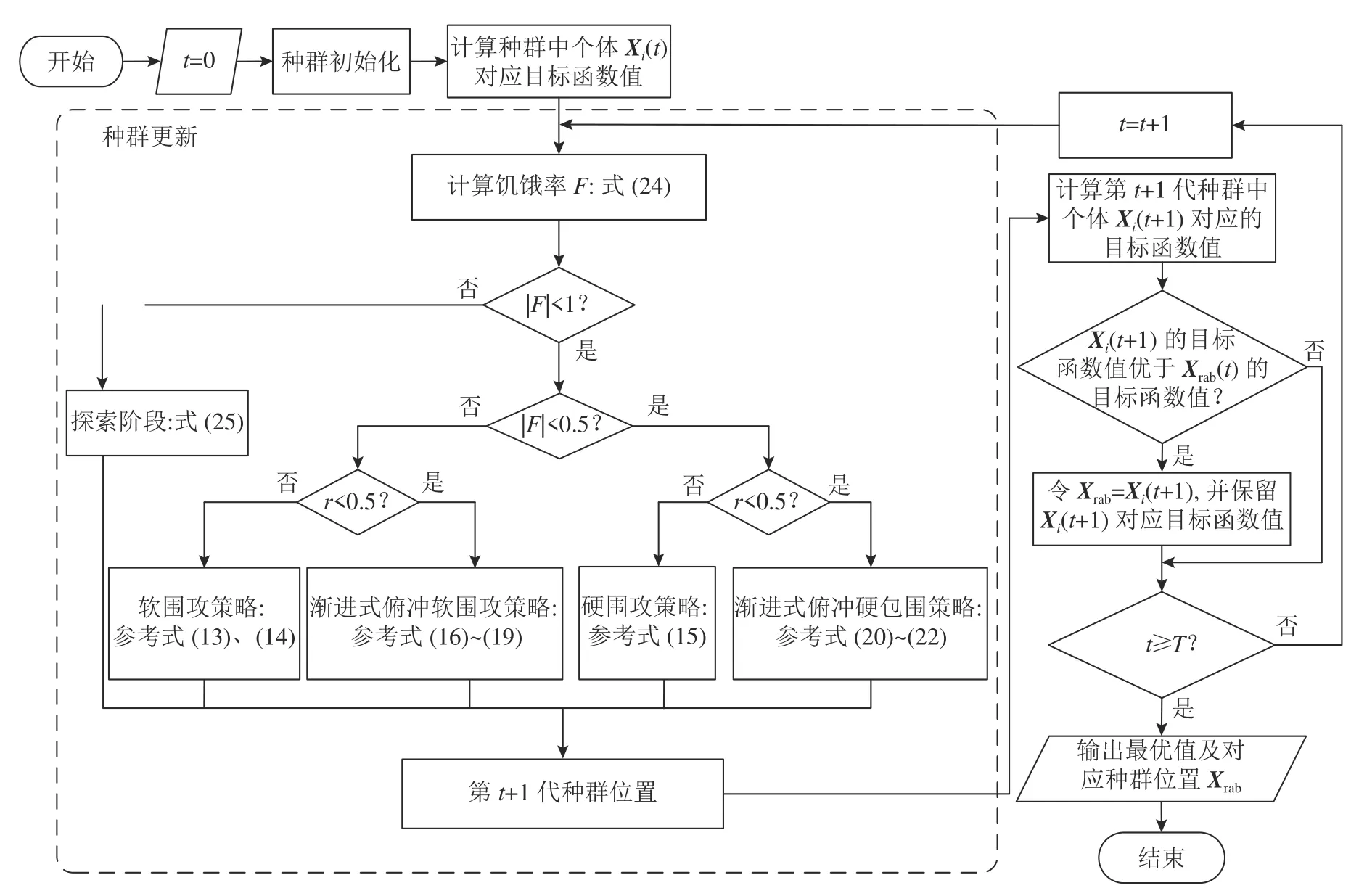
图2 改进哈里斯鹰算法的算法流程图Fig.2 Flow chart of improved Harris hawks optimization algorithm

2.3 改进哈里斯鹰算法的函数测试

PSO、GA 具有较强的可比性、代表性及普适性，GWO 具有参数较少、寻优性能强的优点.为了评估H U H H O 的寻优性能，进行4 种算法（PSO、GA、GWO、HHO）在4 个典型测试函数（Rastrigin、Ackley、Foxholes 和Kowalik）中的收敛精度、收敛速率及稳健性对比分析.其中Rastrigin和Ackley 属于多模态基准函数，Foxholes 和Kowalik属于定维多模态基准函数.上述基准函数的具体表达式、变量范围和最优解详见文献[30].相关参数设置如下：种群规模N=30，最大迭代次数T=500.PSO 中的学习因子取c1=c2=2；惯性权重ω 的初始值为0.9，按照迭代次数线性递减到0.4；GA 中交叉、变异概率分别为Pc=0.2、Pm=0.08；GWO 可调参数较少，参照文献[24]设置.

利用不同算法对各测试函数进行30 次独立运算，取不同算法计算结果的平均值Mean、标准差Std 作对比，如表1 所示.在4 个测试函数中，HHO 平均值及标准差显著优于PSO、GA 及GWO，而HUHHO 则优于HHO.如图3 所示为不同测试函数收敛过程曲线.可以看出，HHO 在迭代次数小于50 的情况下即已收敛，收敛速度明显快于PSO、GA 和GWO；HUHHO 的收敛速度比HHO 更快.测试结果表明，与PSO、GWO、GA、HHO 相比，本研究提出的HUHHO 求解精度更高、收敛速度更快、稳健性更强，该算法能够在多维优化问题中获得更好的寻优性能.

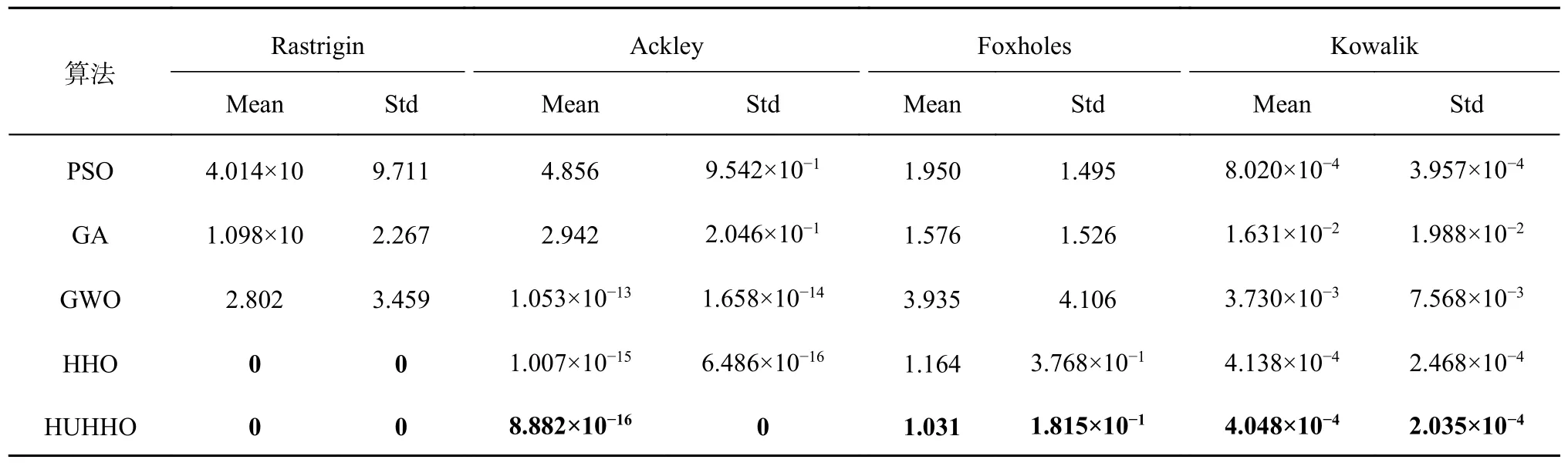
表1 不同算法优化性能测试Tab.1 Optimization performance test of different algorithms

图3 不同算法在测试函数中的收敛过程曲线Fig.3 Convergence curves of different algorithms with different test functions

3 基于改进哈里斯鹰算法的梯级泵站优化调度模型求解步骤

基于HUHHO 的梯级泵站优化调度主要流程包括初始化、约束处理和更新迭代，其中更新迭代采用HUHHO 种群更新机制.

3.1 种群个体结构及初始化

对于单级泵站流量优化模型，决策变量为单级泵站各水泵流量.决策变量向量描述为

式中：k∈[1，n]，Qj,k为第j级泵站中第k台水泵流量，

式中：α∈[0，1]，Qj,k(min)、Qj,k(max)分别是第k台单泵的最小和最大流量.

对于梯级泵站扬程优化模型，决策变量为各单级泵站的扬程，由泵站进出池水位进行向量描述：

式中：j∈[1，b]，Zin,j、Zout,j分别为第j级泵站进、出水池水位，

式中：Zout,j(min)、Zout,j(max)分别为第j级泵站出水池允许最低及最高运行水位.

初始化即个体的各维在对应的最大值和最小值之间产生.通常，这些新生成的个体不满足所有约束，为此使用约束处理方法进行修正.

3.2 基于改进哈里斯鹰算法的梯级泵站优化调度约束处理

梯级泵站优化调度运行存在许多等式约束和不等式约束，处理这些约束是有效求解梯级泵站优化调度模型的关键.在HUHHO 中，不等式约束易于处理，超出边界的值可以简单设置为等于边界.而等式约束的处理相对困难，包括单级泵站流量优化模型中的流量平衡约束（式（2））和梯级泵站扬程优化模型中的水力平衡约束（式（6））.本研究对于所有算法均采用Tian 等[31]提出的策略处理等式约束.以流量平衡约束为例，先计算式（2）两侧差值，将差值平均分配给各水泵以调整流量，判断新产生的各水泵流量是否违反边界条件，如果是，则再次处理不等式和等式约束.通过不断分配差值及判断，使各水泵流量满足一定精度下的等式及不等式要求，此处精度取小数点后4 位.

3.3 基于改进哈里斯鹰算法的梯级泵站优化调度流程

基于HUHHO 的梯级泵站优化调度流程如图4所示.

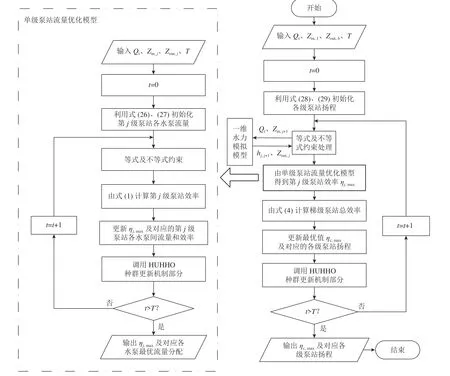
图4 基于改进哈里斯鹰算法的梯级泵站优化调度模型求解流程图Fig.4 Flow chart of optimal scheduling of cascade pumping stations based on improved Harris hawks optimization algorithm

4 实例计算

以北京市某包含三级泵站的梯级泵站调水系统为例，其工程示意图如图5 所示.每级泵站均包含4 台立式轴流水泵（3 用1 备）.泵站1：水泵转速为245 r/min，电动机功率为315 kW，总装机容量为1 260 kW.泵站2：水泵转速为245 r/min，电动机功率为355 kW，总装机容量为1 420 kW.泵站3：水泵转速为245 r/min，电动机功率为400 kW，总装机容量为1 600 kW.第一级泵站进水池设计水位为48.60 m，第三级泵站出水池设计水位为51.82 m，假设二者为定值.单位电价取当地阶梯电费的加权平均值0.847 8 元/（kW·h）.上述三级泵站调水系统现状方案如表2 所示，其中Hn为泵站毛扬程.

图5 某三级泵站工程平面图Fig.5 Schematic diagram of cascade pumping station in three-stage pumping station

4.1 不同算法对比

PSO 与GA 为经典元启发式算法，被广泛应用于电力、人工智能、机械、水利等学科领域，且在工程优化调度问题中表现出色.本研究选取PSO、GA 与HHO 和HUHHO 进行对比分析，以验证HUHHO 在梯级泵站优化调度领域中的性能.梯级泵站扬程优化模型中最大迭代次数与种群大小分别取50、30，单级泵站流量优化模型中最大迭代次数与种群大小分别取100、30.PSO、GA 的参数设置同前文一致.

根据设定参数及已知条件，采用不同算法进行优化计算.算法寻优具有一定随机性，单次计算结果不具普适性、缺乏说服力，多次计算取其最好结果则有失一般性，为此取多次计算得到的平均结果作为最终结果，以最大程度反映算法寻优性能.由于梯级泵站系统存在复杂的水力、机械与结构联系，对多次计算所得结果（梯级泵站最大运行效率）取平均后的方案可能无法满足上述联系，本研究将模型独立计算5 次，取梯级泵站最大效率中位数所对应结果作为最终结果.将基于各算法优化方案下的梯级泵站效率与运行费用进行对比，结果如图6 所示.由图可知，利用PSO、GA、HHO 及HUHHO 优化得到的梯级泵站效率分别为34.11%、34.12%、34.15%、34.20%，相较于现状方案分别提高了0.02、0.03、0.06 和0.11 个百分点.各方案运行费用为梯级泵站调水系统有效输出功率、运行时长和单位电价三者之积与梯级泵站运行效率的比值[32]，年节约成本W为优化方案与现状方案年运行费用之差.因此，基于PSO、GA、HHO 及HUHHO 的优化方案对应年节约成本分别为7 074、10 985、22 703、42 187 元.基于H U H H O 的优化方案优于采用P S O、G A 和HHO 的优化方案，表明所提出算法改进策略有效，且改进效果较优.

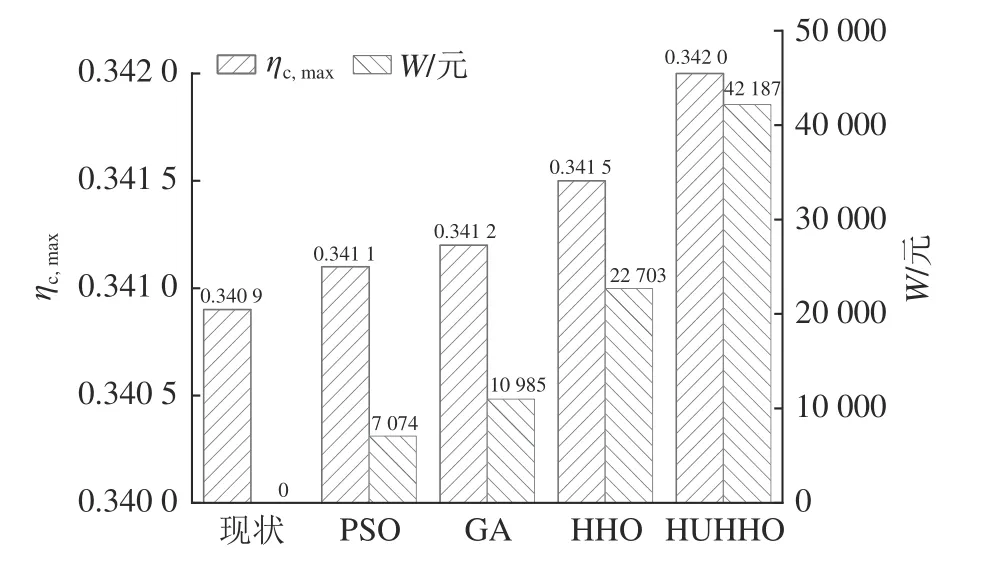
图6 基于不同算法的优化效果对比Fig.6 Comparison of optimization effects for different algorithm

基于不同算法的优化方案对应的各级泵站中各水泵流量与效率、各级泵站运行效率、各级泵站扬程和泵站间水头损失等如表3 所示.该梯级泵站调水系统净扬程为3.22 m，为低扬程梯级泵站系统.采用PSO、GA、HHO、HUHHO 得到的优化方案对应的总水头损失分别为1.62、1.57、1.58、1.52 m，对应毛扬程分别为4.84、4.79、4.80、4.74 m，据此可得二者比值分别为0.334 5、0.327 3、0.328 6、0.320 8.通常情况下，低扬程梯级泵站调水系统中水头损失在总扬程中占比越大，其系统效率越低，因此，同采用HUHHO 的优化方案相比，基于其他算法所得优化方案的梯级泵站系统效率偏低.

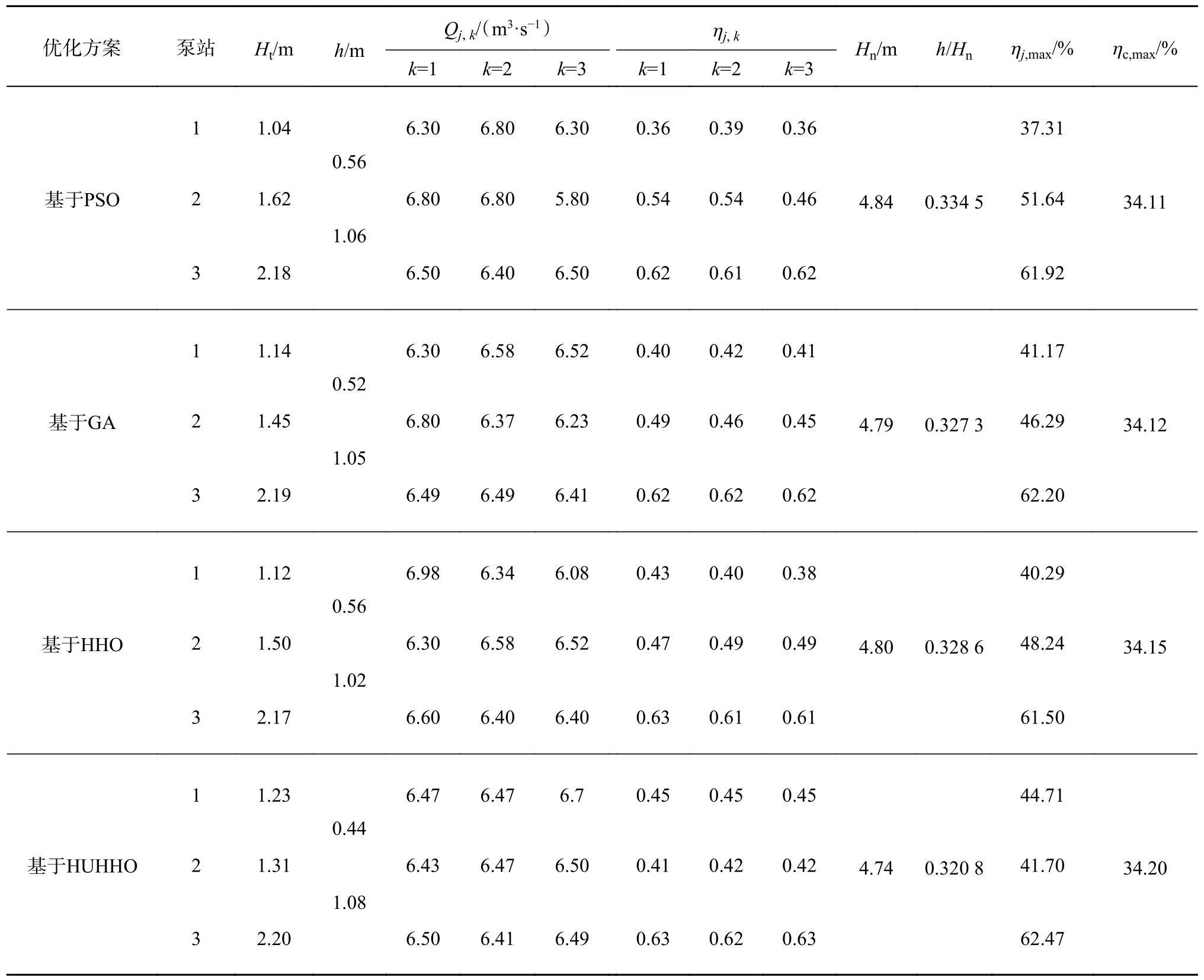
表3 基于不同优化算法的梯级泵站优化结果Tab.3 Optimization results of cascade pumping station based on different algorithms

4.2 改进策略作用分析

如图7 所示为HUHHO 和HHO 迭代次数与运行效率的关系.由图可以看出，相比于HHO，HUHHO 的收敛速度更快，在经历21 次迭代后HUHHO 达到收敛，小于HHO 的28 次.HUHHO 达到收敛后梯级泵站运行效率为0.342 0，高于HHO 的0.341 4.因此，改进策略的实施令HUHHO在收敛性能上得到提升，改善了系统运行效率.

图7 哈里斯鹰算法改进前后收敛过程对比Fig.7 Comparison of convergence process based on Harris hawks optimization algorithm before and after improved

4.3 算法搜索性能分析

对于智能算法而言，一般增大种群规模或迭代次数可进一步改善优化效果.过大的种群规模与迭代次数会占用更多的计算机内存、极大延长寻优时间，而种群更新迭代后期算法优化效果提升甚微.高效的算法能够在较小的种群规模下经过一定的迭代次数收敛至全局最优或者准全局最优解.本研究基于不同种群规模与最大迭代次数的计算结果进一步论证HUHHO 在搜索性能方面的优越性.相关优化结果如表4 所示.由表可知，HUHHO 在种群规模30、扬程优化模型最大迭代次数Th=5 0、流量优化模型最大迭代次数Tq=50 下，计算所得梯级泵站最大运行效率为0.341 6，其数值高于PSO、GA、HHO 在相同种群规模与扬程优化模型最大迭代次数，但流量优化模型最大迭代次数为100 时，计算所得梯级泵站最大运行效率为0.341 1、0.341 2、0.341 5.上述结果表明，PSO、GA、HHO 均不同程度地陷入了局部最优解，而HUHHO 在克服算法“早熟”方面的性能明显更优.计算结果虽然遵循种群规模及迭代次数越大、收敛值越大，梯级泵站最大运行效率越高、寻优效果越好的规律，但随着种群规模及迭代次数的增大，收敛值相差较小，由此进一步说明HUHHO 收敛速度快，可以在较小种群规模下经过一定迭代次数达到较满意的精度.HUHHO 的高效性得以验证.

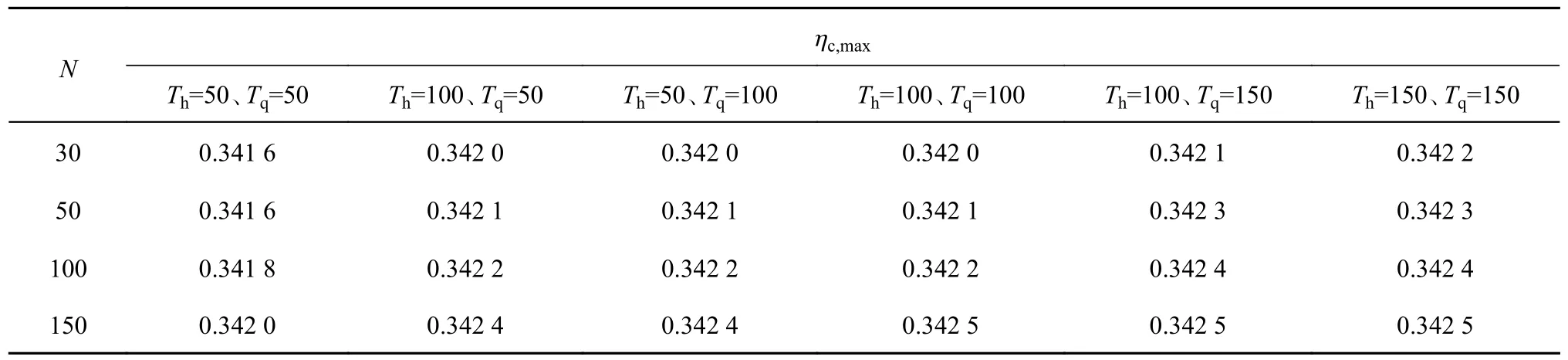
表4 改进哈里斯鹰算法于不同种群规模与最大迭代次数下的优化结果Tab.4 Optimization results by improved Harris hawks optimization algorithm in different population sizes and maximum iterations

结合实验分析可知，基于HUHHO 的优化结果对仅有的种群规模与迭代次数2 个人为设定参数不敏感.因此，相比PSO、GA、HHO，HUHHO 能够有效降低参数不确定性对优化结果产生的影响，该算法在梯级泵站优化调度中具有较强的鲁棒性.

4.4 优化效果的分析与讨论

通过对比基于不同优化算法的梯级泵站优化结果可知，采用PSO、GA、HHO 和HUHHO 的优化方案均优于现状方案，且HUHHO 整体表现更为突出.须指出，各优化方案的优化幅度相对有限，原因主要有1）选取工程为低扬程梯级泵站调水工程，工程净扬程为3.22 m，总水头损失与毛扬程比值超过0.3，在扬程优化层面，算法优化空间较小，且各泵站内采用同类型水泵，故在流量优化层面算法优化空间也较为有限；2）梯级泵站运行过程中，各建筑物及水力设施间的复杂水力关系长期存在，且泵站内各机组流量与各泵站间的扬程组合受多因素影响，因此整体优化难度较大.

梯级泵站广泛存在于农田灌排、城市给排水及跨流域调水等领域，承担着区域性防洪、灌溉、调水和供水等重任，即便是较小的优化幅度，考虑到行业的整体规模，带来的潜在经济效益和社会效益亦不容忽视.鉴于不同梯级泵站调水工程运行调度的相似性及HUHHO 的高效性，可将HUHHO 推广应用至其他类似梯级泵站的优化调度中，发挥更大的实际应用价值.

5 结 论

（1）HUHHO 在Rastrigin、Ackley、Foxholes 和Kowalik 4 个测试函数中计算的平均值与标准差显著优于PSO、GA、GWO 及HHO，且更快完成收敛，表明HUHHO 收敛精度更优、鲁棒性更强、收敛速度更快，验证了改进策略的有效性.

（2）基于HUHHO 的优化方案，其系统运行效率为34.20%，年运行成本较现状方案节约42 187元，优于利用PSO、GA 及HHO 所得优化方案，证明了所提方法的可行性和优越性，能够为梯级泵站优化调度问题提供更高效、更经济的方案.

（3）基于HUHHO 的优化方案在一定程度上提升了梯级泵站系统运行效率，但是低扬程梯级泵站系统的优化空间相对有限，且级间水力联系复杂，系统运行效率提升难度大，因此所提方案的优化幅度相对较小.

（4）本研究是将新型优化算法应用于梯级泵站优化调度领域的探索，并未考虑高扬程梯级泵站系统，且优化目标仅考虑系统运行效率.未来将针对不同扬程、流量梯级泵站系统，考虑能耗、运营成本等目标，开展多目标优化调度研究，为梯级泵站系统运行提供更加全面的优化方案.