基于多门控混合专家网络的燃烧热化学流形表征

王意存，邵长孝，金台，邢江宽，罗坤,4，樊建人,4

(1.浙江大学 能源高效清洁利用全国重点实验室，浙江 杭州 310027；2.哈尔滨工业大学（深圳） 湍流控制研究所，广东 深圳518055；3.浙江大学 航空航天学院，浙江 杭州 310027；4.浙江大学 上海高等研究院，上海 200120)

机器学习（machine learning，ML）方法已经在以计算流体力学（computational fluid dynamics，CFD）为代表的科学计算领域掀起了热潮[1].在湍流燃烧数值模拟方面，研究者试图用机器学习方法进行燃烧建模[2-4]，建立数据驱动的燃烧模型.热化学流形（thermochemical manifolds）的参数化和表征是机器学习在燃烧建模中的重要应用.传统的流形参数化技术包括各种查表（loop-up tables）技术，如原位自适应建表（in situ adaptive tabulation，ISAT）[5]、分段多项式近似（piecewise polynomial approximation）[6]以及小火焰模型（flamelet models）[7].人工神经网络模型（artificial neural network，ANN）因更快的计算速度和更小的内存占用，在热化学流形的参数化和表征方面已经得到研究和认可.因为基于神经网络的模型只需存储网络结构信息、权重和偏置参数[8]，所以通常不会占用太多存储空间.除此之外，与传统的查表方法不同，基于神经网络的模型具有采样点之间平滑插值的优点[2,3,9].

基于机器学习已经发展出一些新型的热化学流形表征方法.在有限速率类燃烧模型方面，求解化学反应刚性常微分方程组（system of ordinary differential equations，SODEs）使用详细化学反应机理直接积分（direct integration，DI）方法的计算量巨大，导致计算效率较低.为此，研究者利用神经网络模型建立热化学状态作为输入和化学反应源项（或者下一时刻的状态）作为输出的映射关系[2,10-15].为了使神经网络具有良好泛化能力，训练数据集必须覆盖真实模拟中可能遇到的热化学状态，复杂的反应机理会对热化学状态数据集的构建以及神经网络的训练带来困难[2].替代方案是在小火焰燃烧模型框架下实施热化学流形表征，这也是本研究的焦点.

在小火焰燃烧模型框架内，通常利用几个控制变量（controlling variable）（如混合分数、过程变量）来参数化低维流形[16]，待求解的热化学标量通过预先建立的小火焰库访问而无需求解组分输运方程，因此具有较高的计算效率.然而，在一些复杂场景中（如考虑辐射和相间换热、多进口构型），必须对小火焰模型进行维度扩展、增加控制变量的数量[16]，此时会造成小火焰库的尺寸较大，读取这些小火焰库需要占用较大的内存空间以及复杂的多维插值程序.为此，研究者利用ANN 建立控制变量作为输入、其他热化学标量作为输出的映射关系.CFD 程序读取训练好的ANN 而非小火焰库，从而缓解内存占用问题.此类方法已成功应用于值班CH4/air 射流火焰[9]、钝体旋流稳定火焰[17]、CH4/H2/N2射流扩散火焰[18]、具有非均匀入口的值班射流火焰[19]、火箭发动机[20]、内燃机工况下的喷雾火焰[8,21]、超声速燃烧器[22]和超临界CO2燃烧器[23]等.

基于小火焰的燃烧热化学流形表征完成的都是从较少几个控制变量到热化学标量的映射，其中基础的前馈神经网络（feedforward neural network，FNN）得到最多的应用.从机器学习的角度，该问题可视作多任务学习问题，任务目标是使得各个热化学标量都取得较好的预测精度.Owoyele等[24]采用混合专家网络（mixture of experts，MoE）[25]完成了燃烧流形表征，并取得较好的先验结果.MoE 是典型的多任务学习技术，由于只有1 个门控网络，在任务相关性不强的问题中可能表现不佳.对于相关性不强的多个任务，多门控混合专家网络（multi-gate mixture of experts，MMoE）[26]的表现更好.因此，从理论上讲，MMoE 比MoE 更加适用于燃烧热化学流形的表征.本研究采用MMoE 模型在小火焰模型框架内实现燃烧热化学流形的表征，获取比FNN 模型更高的精度.本研究模型训练采用的数据集来自三维层流射流喷雾火焰的详细化学（detailed chemistry，DC）模拟，本研究将对该数据集中的组分进行相关性分析，分别搭建MMoE 和FNN 模型，将2 种模型的结果与DC 结果对比以进行性能评估.

1 数学和物理模型

1.1 详细化学模拟

训练和测试用的数据由DC 模拟计算得到.在喷雾燃烧DC 模拟中，通过直接求解质量、动量、能量和组分质量分数的守恒方程建立数据库.基于低马赫数假设，守恒方程为

式中：ρ 为气相密度，基于理想气体状态方程求解；uj为气相速度；p为压力；τi j为黏性应力；wk为组分k的质量分数；h为比焓；α 为热扩散系数；D为组 分 扩 散 系数； ω ˙h为燃 烧 热释 率； ω ˙k是 组分k的反应速率；δlk为Kronecker 记号，其中l为液相蒸发的组分；Ns为系统中化学组分总数；S˙ρ、S˙ui和S˙h分别为液相的质量、动量和能量源项，基于点源模型（particle-source-in cell，PSI-Cell）封闭[27-29].液相采用拉格朗日颗粒追踪方法（Lagrangian particle tracking，LPT）计算求解[30].

1.2 小火焰燃烧模型

根据Wang 等[31-33]提出的两相喷雾小火焰过程变量（two-phase spray flamelet / progress variable，TSFPV）模型，热化学标量ψ 可以参数化为

式中：Z、C和Zcarr分别为混合分数、过程变量以及新定义的载气混合分数（carrier mixture fraction）[31].这3 个控制变量须在CFD 程序中同步求解，守恒方程分别为

式中：C为过程变量，C=wCO2+wH2O+wCO+wH2，w为 质 量 分数； ω ˙C为过 程变 量 源 项；DZ、DC分 别为混合分数和过程变量的扩散系数；载气混合分数Zcarr是被动标量，其守恒方程中没有源项，可以避免传统混合分数Z的非单调性相关问题[31,34-36].

1.3 三维层流喷雾射流火焰数据集

使用OpenFOAM 7.0 中的喷雾燃烧求解器sprayFoam，对三维层流喷雾射流火焰进行详细化学模拟，构建DC 数据集，以用于神经网络模型的训练和测试.火焰构型的示意图如图1 所示.中心射流直径D= 1 mm，射流包括空气、甲醇液滴以及预汽化的燃料蒸汽组成的混合物.射流周围的伴随流由氢气/空气在1 430 K 的贫燃平衡产物组成[37].射流入口速度为8 m/s，特征长度取中心射流直径，取运动黏度为1.5×10-5m2/s，计算得到射流入口雷诺数为533，小于圆管流动临界雷诺数为2 300，可以认为当前研究的火焰为层流火焰.伴随流入口速度为1 m/s，液相质量流量为3.185×10-6kg/s.其他的入口参数参见表1.入流参数的设置参考悉尼抬升甲醇喷雾火焰Mt2A 构型[37-38].计算域是直径为30D，流向长度为55D的圆柱体，采用的总网格数约为105 万.采用的化学反应机理为甲醇燃烧的18 组分55 步反应骨架机理[39].

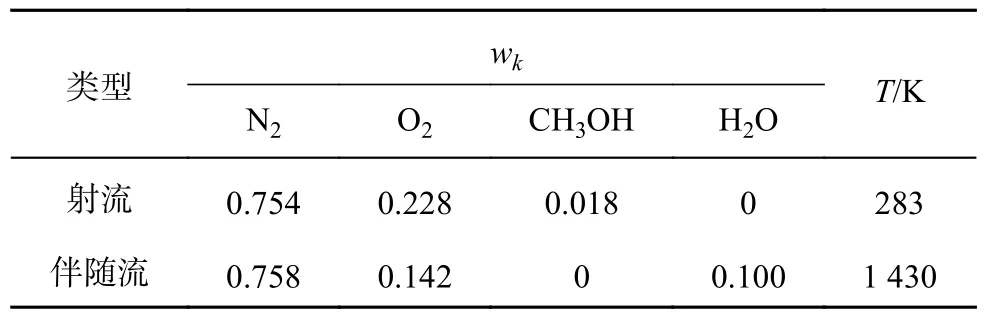
表1 喷雾射流火焰的入口参数Tab.1 Inflow parameters of spray jet flame

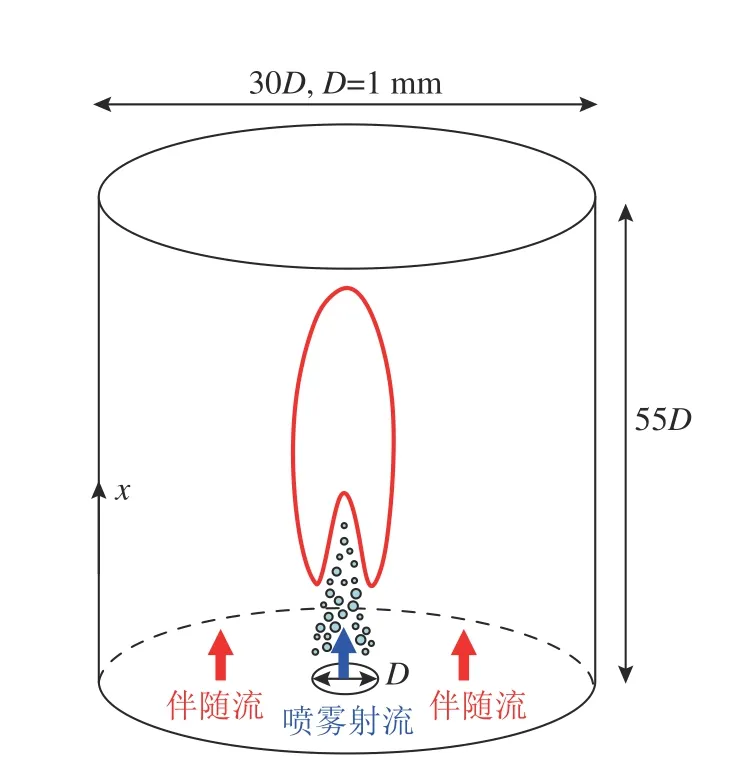
图1 喷雾射流火焰构型示意图Fig.1 Schematic of configuration of spray jet flame

对于DC 模拟生成的原始数据集，须进行数据预处理操作，预处理过程包括2 个步骤.1）组分质量分数、Z、C和Zcarr介于[0, 1]，采用Box-Cox转换（Box-Cox transformation，BCT）[11,40]，将物理量映射至O(1)量级，解决燃烧数据的多尺度分布问题.2）对所有BCT 后的热化学标量，使用Z-score标准化处理.对于预处理过的数据样本，随机选取其中80%作为训练集，20%作为测试集.

1.4 人工神经网络模型

FNN 也称多层感知器（multi-layer perceptron，MLP），是应用广泛的基础人工神经网络，如图2(a)所示.FNN 中各神经元分别属于不同的层，每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层.第0 层称为输入层，最后一层称为输出层，其他中间层称为隐藏层.每个神经元视为从输入到输出的非线性映射.输入层神经元接收的输入是整个网络的输入值，在当前问题中也就是控制变量X=[Z,C,Zcarr].对于中间层神经元，输入是前一层神经元的输出.对于输出层的神经元，输出就是待求解的热化学标量φ.整个网络的运算关系为

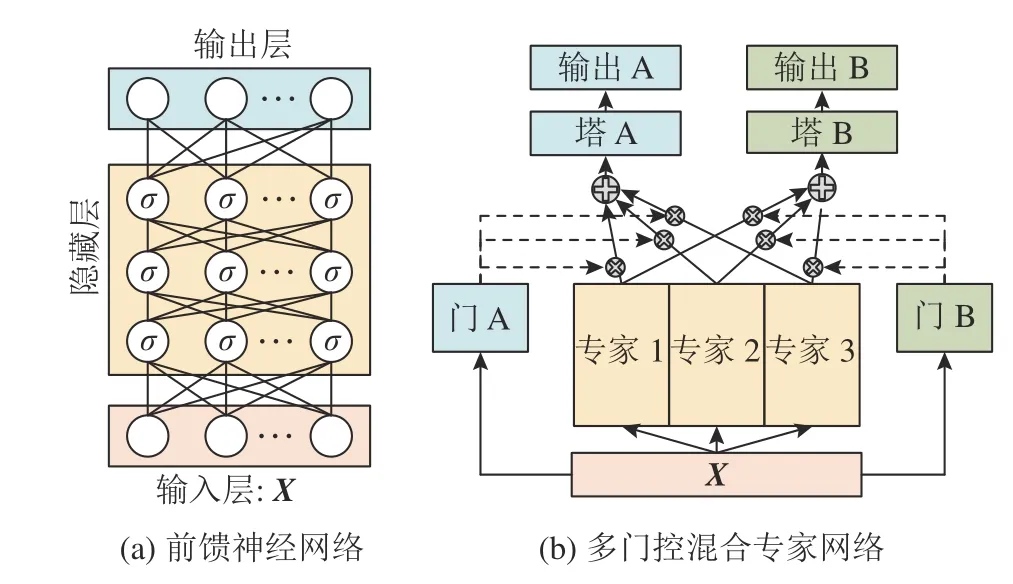
图2 神经网络示意图Fig.2 Schematic of neural network

神经网络模型基于开源PyTorch 1.8.2 框架实现.为了公平比较2 种网络模型的性能，保持网络结构具有相近的可训练参数数目.对于2 种网络结构，网络输入包含3 个控制变量，即Z，C和Zcarr，网络输出为17 变量，即去除N2之后的17 个组分.对于FNN，网络包含7 层隐藏层，隐藏层神经元数目为(8, 16, 32, 64, 94, 64, 32)，隐藏层激活函数为tanh，总的参数数目为17 663.对于MMoE，网络结构包含8 个专家网络，17 个塔网络，17 个门控网络.专家网络和塔网络结构汇总如表2，总的参数数目为17 609.这2 种网络结构都采用均方误差（mean square error，MSE）损失函数.函数网络权重使用Xavier 初始化[41]，通过Adam 优化器[42]进行优化，采用自定义的指数衰减学习率l/l0=5-n/2000，其中n为训练周期数，初始学习率l0=1.0×10-3.

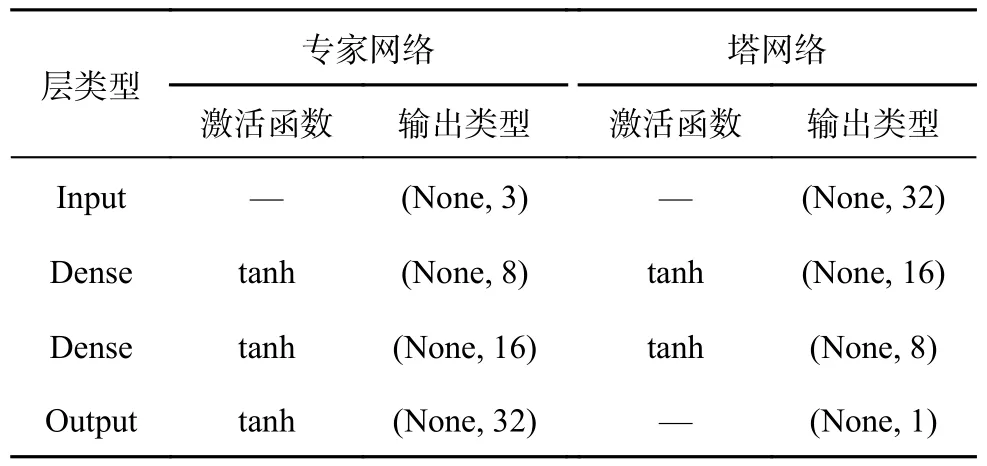
表2 多门控混合专家网络中的专家网络和塔网络结构Tab.2 Structure of expert network and tower network in multi-gate mixture of experts

2 结果与讨论

2.1 火焰数据集分析

分析DC 模拟生成的火焰数据集，标量的分布云图如图3 所示，其中r为径向位置.由图3(a)可以看出，在上游位置（x<10D），主射流和高温伴流之间由于相互混合，形成剪切层.剪切层的高温促进该区域液滴的蒸发，剪切层不断发展，随后着火过程发生并形成火焰.由于液滴蒸发热损失作用导致剪切层温度降低.由图3(b)可以看出，蒸发过程一直持续到约x=20D位置，同时混合分数达到较大值，此时射流中心位置为主要蒸发区域.由图3(d) 可以看出，与经典的混合分数Z不同，Zcarr从射流核心向外单调变化，这将有利于小火焰模型的建模.图3(f)中的白色实线代表等值线wOH= 6×10-4，该等值线可以用于判断火焰抬升高度[43].结果显示火焰抬升高度为6.8D.

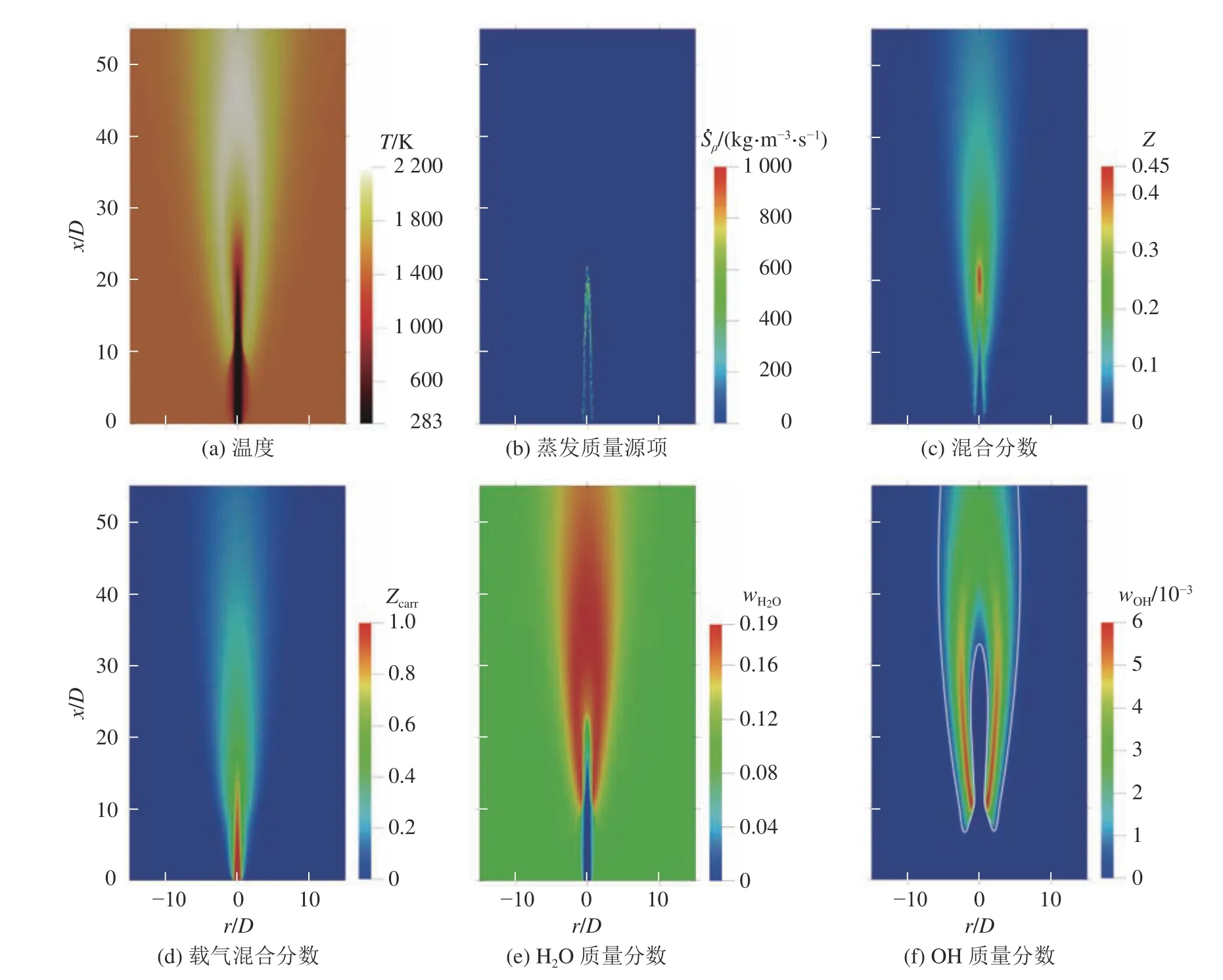
图3 热化学量的等值线云图Fig.3 Contour plots of thermochemical quantities

当前神经网络模型的任务是对除了N2之外的所有组分进行预测，为了挖掘不同组分间的内在相关性，采用Pearson 相关系数（Pearson correlation coefficient）[44]分析预处理后的数据集.2 个变量X和Y之间的相关系数计算式为

式中：µ为平均值，σ 为标准差，E为期望，cov(X,Y) 为X和Y的协方差.相关系数的值介于[-1, 1]，当λX,Y= 0 时，表示X和Y不存在线性相关关系；当λX,Y接近1 或-1 时，表示2 个变量存在较强的正相关或负相关的线性关系.计算任意2 种组分的相关系数并取绝对值，绘制组分相关系数的热力图，如图4 所示.图中，深色方块对应的2 个组分之间的相关系数绝对值接近1，浅色方块对应的2 个组分之间的相关系数绝对值接近于0.可以看出，部分组分之间无明显的相关性.从理论上讲，使用MMoE 而非经典的FNN 将获得更好的预测结果，原因是MMoE 比FNN 更善于处理相关性不强的多个任务[26].

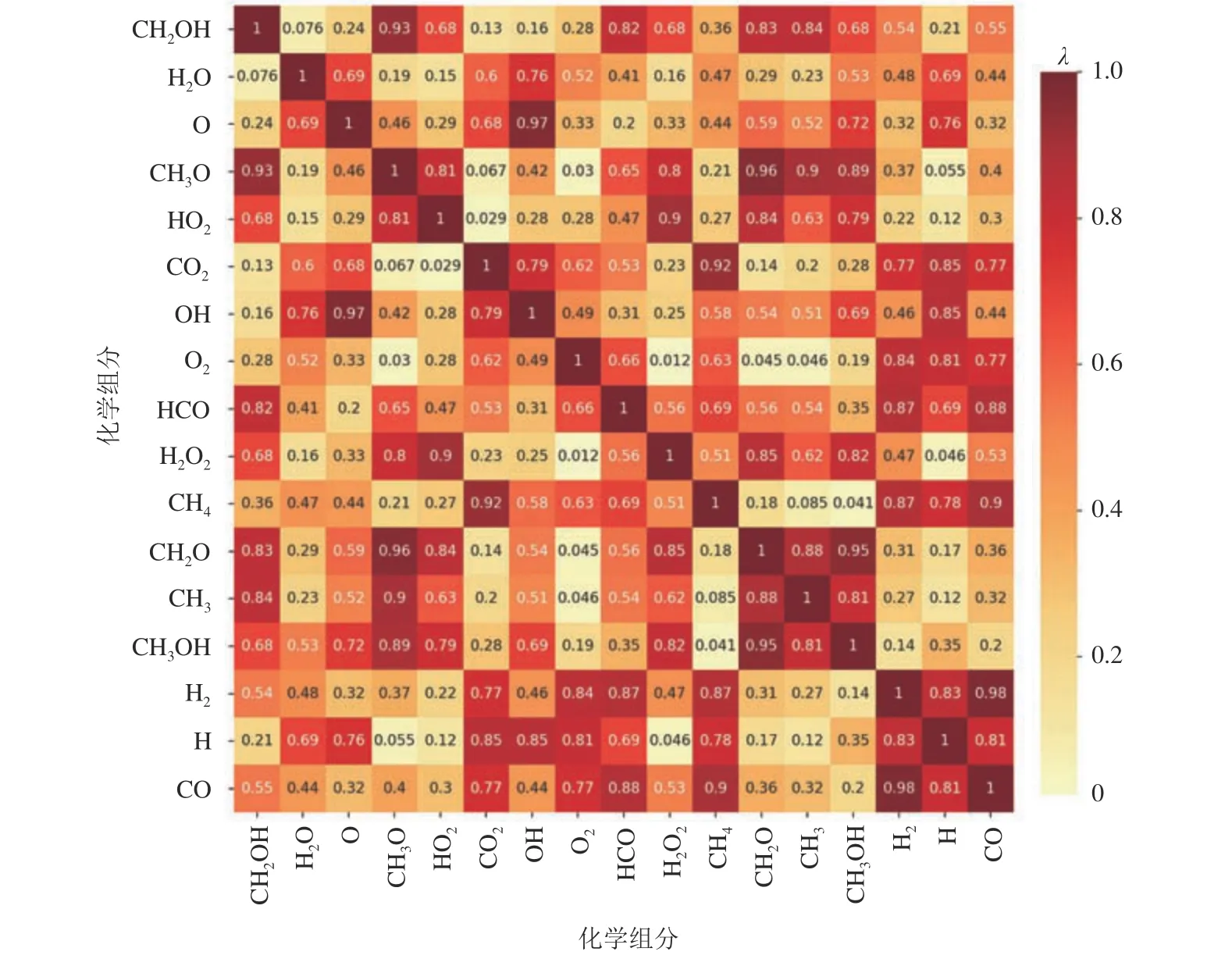
图4 组分相关系数的热力图Fig.4 Heatmap of correlation coefficients for different species

2.2 模型训练结果分析

使用2 种神经网络模型训练5 000 步后的损失值L汇总于表3.整体来看，2 种网络模型最终均收敛到O(10-4)量级的损失值，且训练集损失和测试集损失接近，未出现过拟合问题.尽管MMoE相比FNN 的损失值更小，但均处于同一量级，二者更明显的差异可以结合如图5 所示的训练过程损失曲线来判断.可以看出，整体上，MMoE 的损失值低于FNN.在训练前期（n< 2 000），FNN 损失下降过程出现明显的振荡，MMoE 损失值稳步下降，说明MMoE 模型在训练过程中更加稳定.

表3 神经网络模型最终的损失值Tab.3 Final loss values for different neural network models

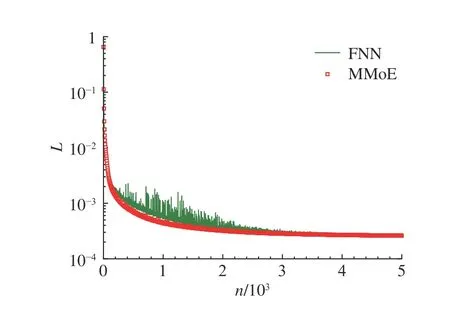
图5 神经网络模型的损失值随迭代步数的变化Fig.5 Loss values versus iterations for different neural networks

如图6、图7 所示分别为2 种模型在测试集上预测值与真实值的散点图.图中，横坐标ytrue为测试集中的真实值，纵坐标ypred为模型的预测值，理想情况下，散点分布在ypred=ytrue对角线上，即图中虚线.散点越接近虚线，表示预测结果越好.可以看出，2 种神经网络模型的预测值都与真实值接近，尤其是质量分数较大的主要组分，例如H2O 和O2.即便是对于质量分数较小的中间组分，例如H2和OH，2 种神经网络模型也展现出不错的预测精度.这说明，对原始数据集的预处理操作（如BCT 转换）可以较好地解决燃烧数据的多尺度分布问题.

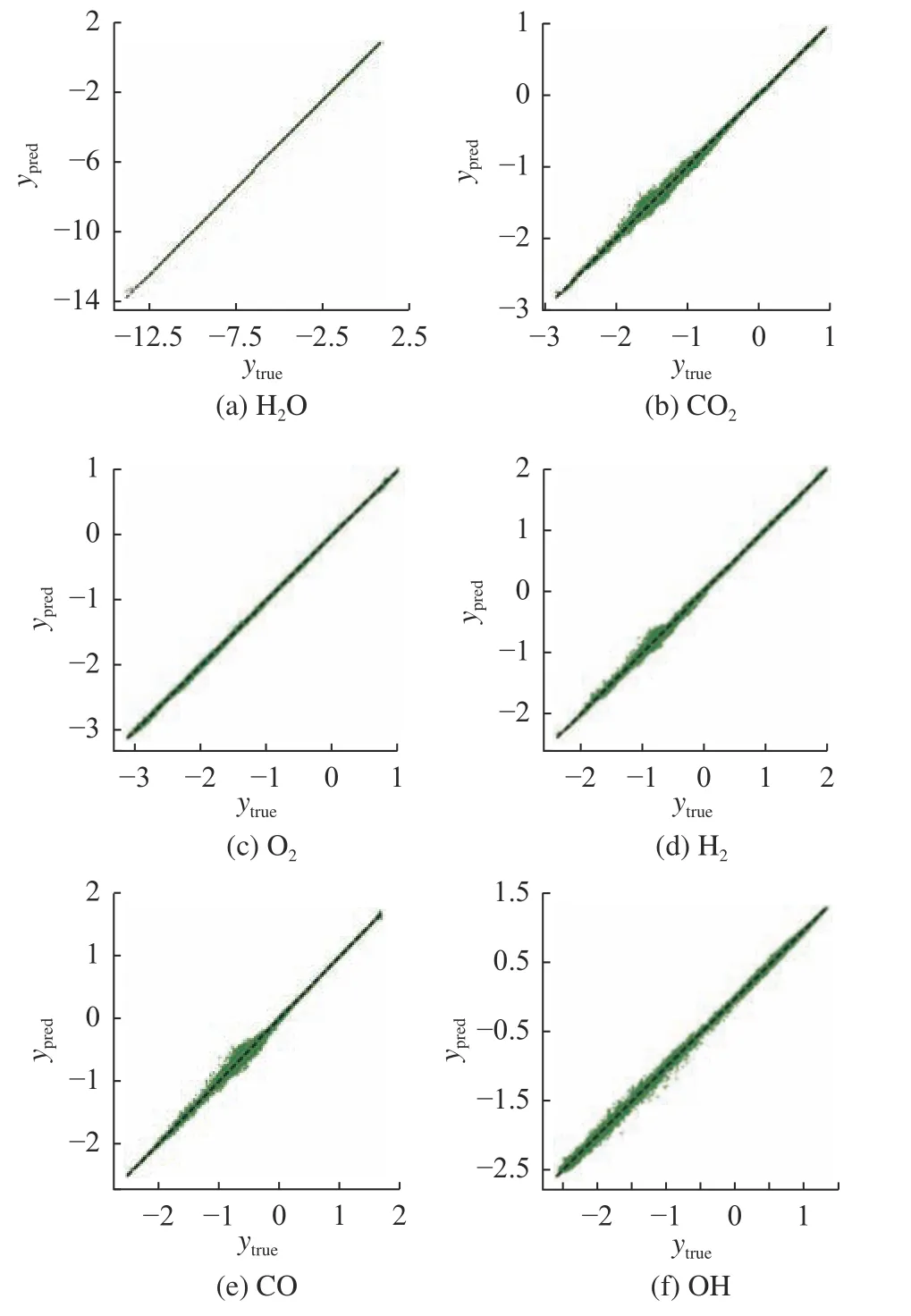
图6 FNN 模型预测值与真实值的散点图Fig.6 Scatter plots of true and predicted values using FNN model

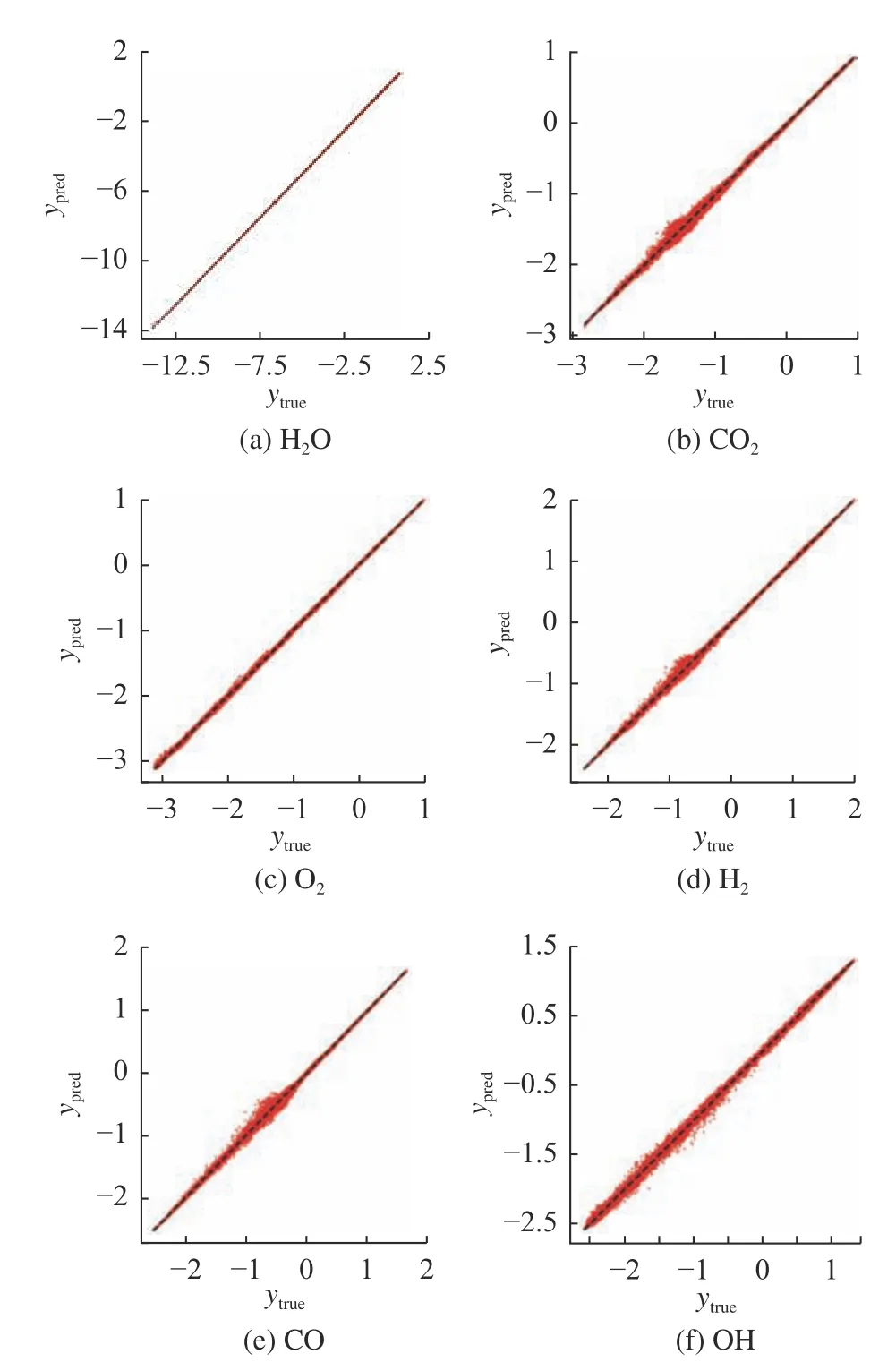
图7 MMoE 模型预测值与真实值的散点图Fig.7 Scatter plots of true and predicted values using MMoE model

采用决定系数（coefficient of determination）R2来定量评估模型的性能，表达式为

式 中：i表 示 第i个 数 据 样 本，y¯true为 真 实 值 的 均值.一般来说，R2越接近1，表示模型拟合效果越好，R2=1 表明模型无误差.2 种神经网络模型在训练数据集和测试数据集上各组分的决定系数汇总于表4.整体上，无论是训练集或测试集，对于所有组分质量分数，2 种神经网络模型的决定系数都高于0.999，这意味着2 种神经网络均得到较好的训练，模型均具有较高的拟合精度.

如图8～10 所示为不同轴向位置处组分质量分数的径向分布曲线.其中H2O、CO2和O2代表主要组分，H2、CO 和OH 为重要的中间产物组分.DC 结果作为基准数据，将FNN 和MMoE 模型的预测结果与DC 结果进行定量对比，以对模型进一步评估.如图8 所示，在上游位置（x=15D），2 种神经网络模型均取得较好的定量预测结果.在下游位置（x=25D、30D），如图9、10 所示，2 种网络模型开始显现出差异.在下游位置，对于主要组分O2，2 种神经网络模型都取得较好的预测结果，对于主要组分H2O 和CO2以及中间产物组分H2和CO，MMoE 模型预测结果更精确，FNN 模型的预测结果出现一定程度的偏差.总体而言，MMoE 模型在上、下游位置，对于各个尺度的组分都有较好的预测精度.MMoE在不同区域均取得较好的预测结果，这得益于MMoE 与MoE 类似，具备多个专家网络，具有燃烧流形自动分支（autonomously bifurcating combustion manifolds）的能力[24].通过门控网络，将不同区域的输入数据分配给不同的专家网络，每个专家网络去处理给定部分的输入，使得MMoE 取得比FNN 更好的局部预测效果.

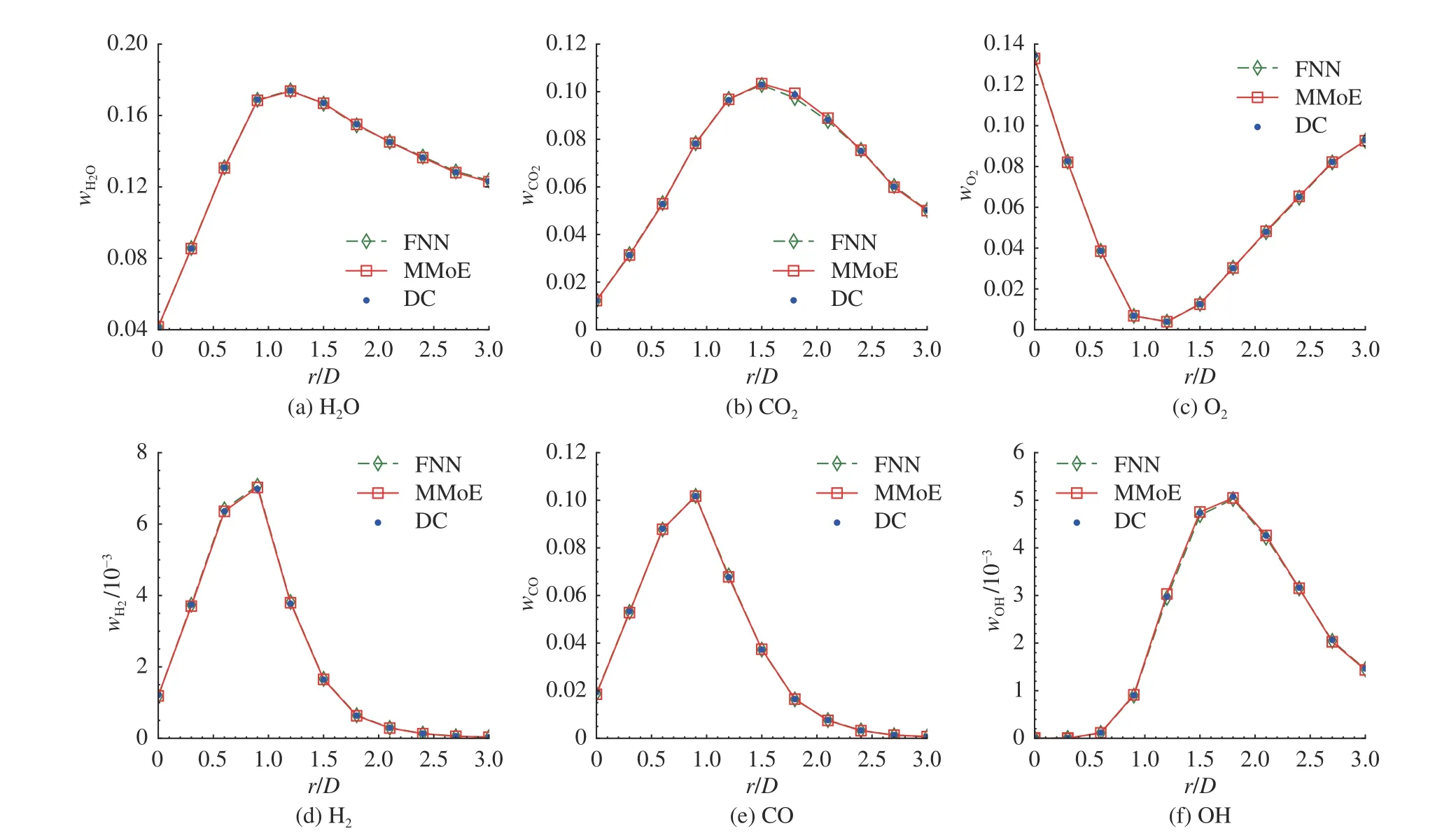
图8 神经网络结果与详细化学结果对比（x/D = 15 位置）Fig.8 Comparisons of detailed chemistry results and solutions using different neural networks at axial location of x/D = 15

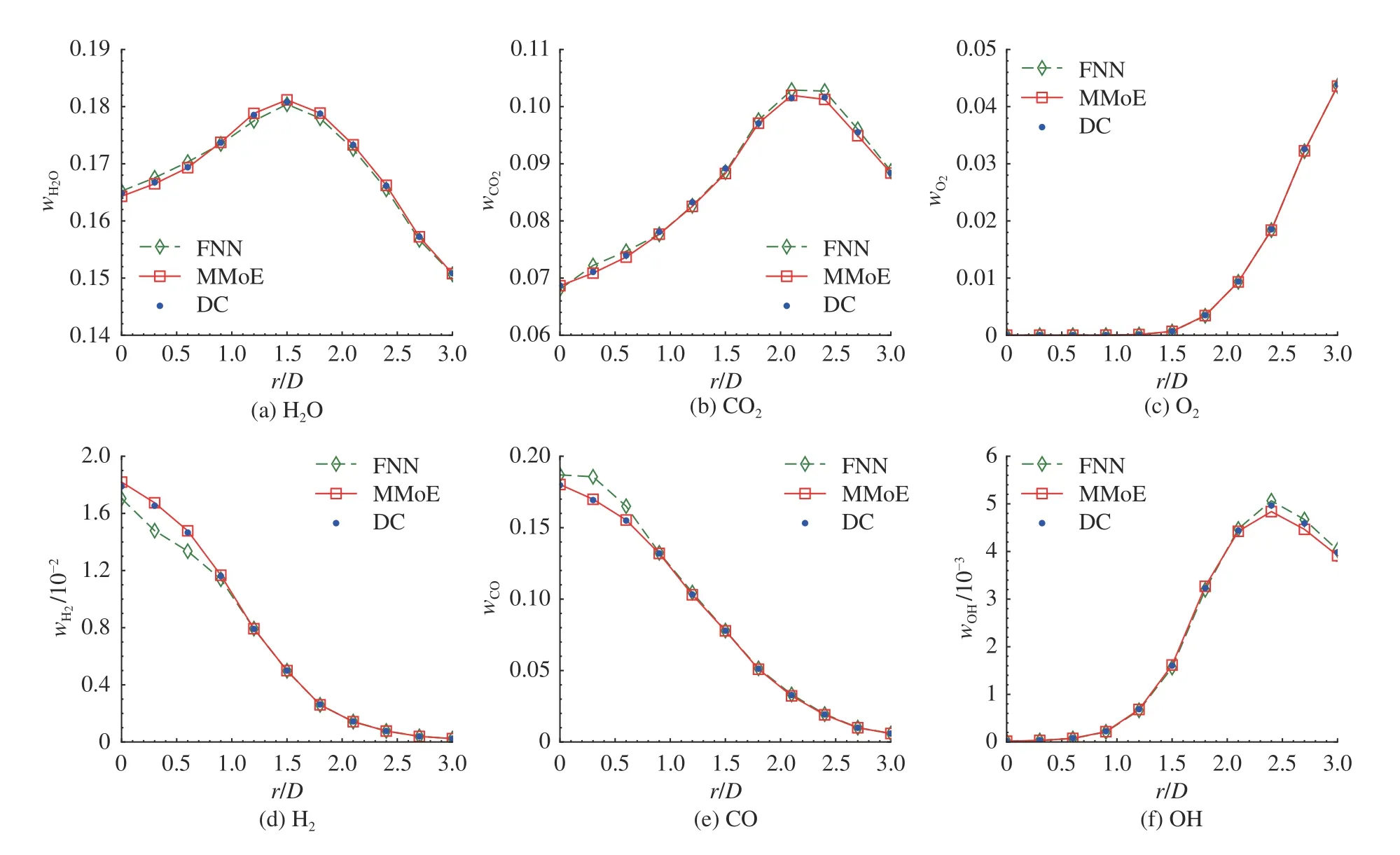
图9 神经网络结果与详细化学结果对比（x/D = 25 位置）Fig.9 Comparisons of detailed chemistry results and solutions using different neural networks at axial location of x/D = 25

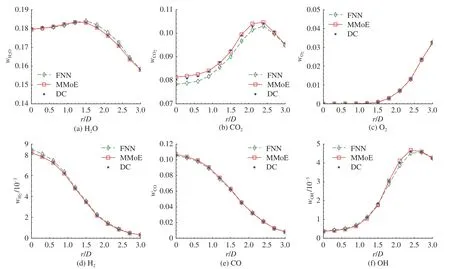
图10 神经网络结果与详细化学结果对比（x/D = 30 位置）Fig.10 Comparisons of detailed chemistry results and solutions using different neural networks at axial location of x/D = 30

为了进一步验证MMoE 相较于FNN 的优势，在1.3 节算例的基础上改变工况，射流入口速度改为4 m/s，伴随流入口速度改为0.5 m/s，温度分布如图11 所示.按照同样的流程构建数据集分别训练MMoE 和FNN 模型，对比分析相应的结果如表5 和图12 所示.结果表明，改变工况后，MMoE依旧取得了比FNN 模型更小的损失值，并且其训练过程更加稳定，这进一步验证了MMoE 的优势.综合此前结果可以得出结论，尽管2 种神经网络模型的损失值和决定系数相似，但MMoE 模型在训练过程中更加稳定，定量预测结果更加准确.

表5 新工况的神经网络模型最终的损失值Tab.5 Final loss values of different neural network for new case

图11 新工况的温度分布云图Fig.11 Contour plots of gas temperature for mew case

图12 新工况的神经网络模型的损失值随迭代步数的变化Fig.12 Loss values versus iterations of different neural networks for new case

3 结 语

本研究将MMoE 模型应用于小火焰燃烧模型框架内的燃烧热化学流形表征.使用OpenFOAM对三维喷雾射流火焰进行详细化学模拟以生成数据集.使用开源深度学习框架PyTorch 分别搭建FNN 和MMoE 模型，并进行对比.结果表明，MMoE 在训练过程中具有更好的稳定性，2 种神经网络模型取得了相近的损失值和决定系数.进一步定量结果表明，MMoE 模型在上、下游位置对于各个尺度的组分都有较好的预测精度，FNN 模型在下游位置出现一定的预测偏差.基于神经网络模型的燃烧热化学流形表征是有前途的新方法，MMoE 模型相较于基础的FNN 模型已展现出一定优势，下一步将进行更加全面的性能评估.此外，作为有效的多任务学习模型，MMoE 对于燃烧机器学习领域的其他问题，例如求解燃烧化学微分方程的物理信息神经网络、热解模型构建等，也有重要的参考价值.

致谢 感谢浙江大学计算机科学与技术学院李玺教授、缪佩翰、励雪巍在研究中给予的帮助.