结合领域经验的深度强化学习信号控制方法
张萌,王殿海,金盛
(浙江大学 建筑工程学院,浙江 杭州 310058)
针对交叉口信号优化控制的研究按照控制方法可划分为3 类:基于历史交通流数据的预定时信号控制[1],基于实时交通状态的响应控制(包括感应控制[2]、自适应控制[3])以及基于模型的协调控制.采用上述方法进行优化交叉口信号控制存在一定的理想假设,具有一定的局限性.随着人工智能技术和交通信息采集技术的发展,通过数据驱动实现信号控制成为交叉口信号优化的新发展方向.
强化学习属于人工智能技术,以马尔可夫决策为基础,通过反馈机制进行学习,适用于具有顺序决策特征的交通信号控制问题.由于交通状态的随机性、复杂性和动态性,传统强化学习在表达交通状态时存在局限.将深度学习与强化学习结合的深度强化学习方法使得强化学习应用于交通信号控制的研究有了新的突破.学者开始应用深度强化学习方法解决交叉口信号控制问题.Genders 等[4]提出使用离散状态编码表示交叉口的交通状态,并使用深度学习中的卷积神经网络提取车辆速度和位置特征.与使用排队车辆数为特征的浅层神经网络相比,Genders 等[4]的方法控制效果更佳,证明了深度卷积神经网络的有效性.Li 等[5]将堆叠自编码器(stacked auto-encoder,SAE)引入强化学习,证明了在减少排队长度上,结合深度学习网络与强化学习的信号控制方法相比于传统的强化学习信号控制方法更有优势.Gao 等[6]基于离散状态编码和深度Q 网络 (deep Q network, DQN)算法进行仿真实验,证明了深度强化学习方法在车辆延误指标上优于最长队列优先(longest queue first, LQF)算法和定时信号控制方法.Mousavi 等[7]使用基于策略和基于值函数的深度强化学习方法控制信号灯;与定时信号控制方法相比,2 种深度强化学习方法均能够显著降低车辆的延误.Wei 等[8]在DQN 算法的基础上提出分区记忆和相位门控机制,在仿真交通流数据和真实交通流数据上验证了所提方法的优越性.Liang 等[9]基于双决斗深度Q 网络(double-dueling deep Q network, 3DQN)[10]算法进行信号优化,采用离散状态编码表示交叉口状态,动作空间为延长5 s 或缩短5 s 某个相位的持续时间;奖励函数采用动作执行前后交叉口内车辆等待时间的差值.孙浩等[11]提出基于深度分布强化学习单交叉口信号控制方法.刘志等[12]通过设计优先级序列经验回放和动作奖惩系数改进深度强化学习算法的性能,所提算法在车辆平均等待时间和路口总排队长度上优于实际配时策略和传统的DQN 算法.刘智敏等[13]构建基于相邻采样时间步实时车辆数变化量的奖励函数,使用改进的DQN 算法进行信号控制.赵乾等[14]基于近端策略优化 (proximal policy optimization, PPO)算法进行单交叉口信号控制并设计NEMA 双环相位结构的动作空间,通过设置低中高交通需求实验验证了所提算法在控制排队长度和车均延误方面优于固定配时方案.
基于深度强化学习的城市单交叉口信号控制的研究在状态定义、动作空间设置、奖励函数、网络结构等方面均进行了较为深入的探索,但在实践中依然存在训练过程不稳定、迭代收敛慢以及动作频繁改变的问题.本研究在深度强化学习算法3DQN 的基础上增加模型预训练模块,通过引入Max-Pressure 方法的经验对智能体的网络进行初始化,在1 步Q 学习损失的基础上引入n步Q 学习损失、监督式边际分类损失和正则化损失,引导智能体模仿Max-Pressure 方法的动作策略,从而得到初始化参数较好的智能体.同时,本研究引入平均车头时距,提出根据排队长度动态设置相位绿灯时间的方法,以减少相位频繁改变带来的绿灯损失问题.以杭州市萧山区机场城市大道和博奥路形成的单交叉口为例,在仿真平台SUMO上对本研究算法进行验证.
1 基于深度强化学习的信号控制方法
1.1 模型建立
深度强化学习模型的结构如图1 所示.强化学习算法包含5 个要素:环境、状态、动作、智能体和奖励.在单交叉口信号控制问题中,一般将交通信号灯抽象为强化学习模型当中的智能体,交叉口处车辆的运行状况看作模型中的环境.基于深度强化学习的交通信号控制方法可以概括为4 个步骤:1)环境将交叉口处的车辆运行状况传递给作为智能体的交通信号灯;2)交通信号灯根据各个车道内车辆的运行状况,做出相应的动作,即激活相应的相位,使得对应方向的车流驶离交叉口;3)动作结束后,交通信号灯收集交叉口车辆的变化情况(如排队长度的变化、延误的变化的反馈信息)作为之前动作的奖励;4)返回步骤1).
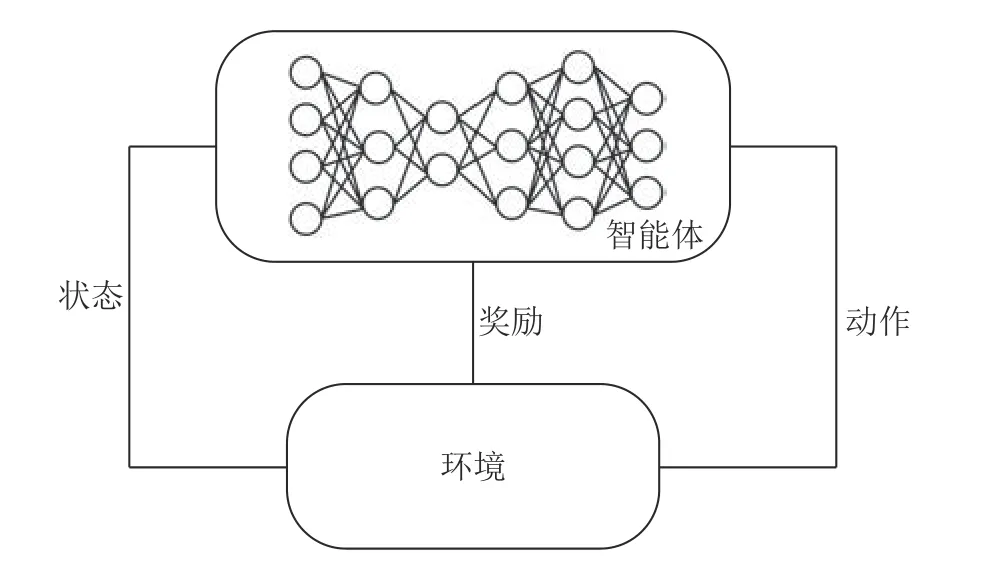
图1 深度强化学习模型示意图Fig.1 Schematic diagram of deep reinforcement learning model
基于深度强化学习算法的智能体通过以上4 个步骤与环境进行不断地交互并在该过程中收集经验,通过策略迭代或值迭代的方式优化自身网络参数,以获得最优的控制策略.为了保证智能体能够学习交叉口处车流的变化并做出合适的动作,须合理定义深度强化学习模型中的要素.本研究以杭州市萧山区机场城市大道和博奥路形成的单交叉口为例,在适当简化交通场景的基础上,依据交通控制领域内的相关指标来设计状态特征、动作和奖励函数.
1.1.1 状态 状态的设计对于深度强化学习模型的学习有至关重要的作用.状态的设计可以分为2 类:1)采用如交通评价指标的统计值来刻画交叉口每条车道内的交通需求以及交通状态(如每条车道的排队长度[15]、交通流量[16]、车流密度[17]等);2)使用图像表示方法对交叉口的每条车道进行离散化编码,即将每条车道划分为长宽固定的元胞,当元胞中含有车辆时,使用与元胞对应的速度矩阵和位置矩阵表示车辆的信息,进而利用卷积神经网络处理矩阵.考虑到状态的维度不宜过大,且使用如交通评价指标的统计值可以达到与图像表示方法同等的控制效果[17],本研究采用状态1)表示方法.结合交叉口的时空因素,采用与交叉口相连的进口道的排队强度Iq,in,车流强度ID,in、车辆平均等待时间强度Iw,in、出口道的排队强度Iq,out、车流强度ID,out、当前相位i的独热编码以及相位绿灯时长是否达到最小绿灯时间作为交叉口的状态特征.其中每条车道的排队强度Iq、车流强度ID、 车辆平均等待时间强度Iw的 定义式为
式中:Nstop为 车道内速度低于0.1 m/s 的车辆;Nmax为单条车道所能容纳的最大车辆数;Nveh为车道内的车辆数;Ti为速度低于0.1 m/s 的每一辆车的等待时间,Tmax为驾驶员容忍的最大等待时间,设定为60 s.以杭州市萧山区机场城市大道和博奥路形成的单交叉口为例,其东西南北方向各有4 条进口道和3 条出口道,总计81 个特征构成该交叉口的状态特征空间,如图2 所示,其中0,···,Pi,···,0 为当前相位i的独热编码,Pi=1.
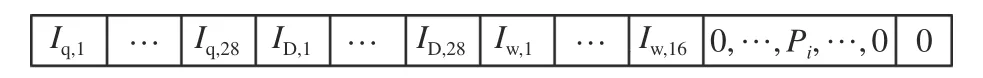
图2 状态向量表Fig.2 State vector scale
1.1.2 动作 动作的设置可以分为4 类:1)设置相位持续时间、2)设置相位绿信比、3)保持或切换当前相位、4)从相位集合中选择某一相位.固定相位相序的动作设置须提前考虑各进口道的车流量制定相位方案.当相位方案改变时,智能体须重新训练.本研究采用动作设置方案4).如图3所示为本研究采用的8 种相位.智能体将在每个决策时刻根据当前状态从动作空间中选取1 种相位.如果选择的相位与信号灯当前相位一致或未达到最小绿灯时长,则延长信号灯显示相位的绿灯时间;否则先执行3 s 黄灯,再根据选择的动作切换至对应的相位.
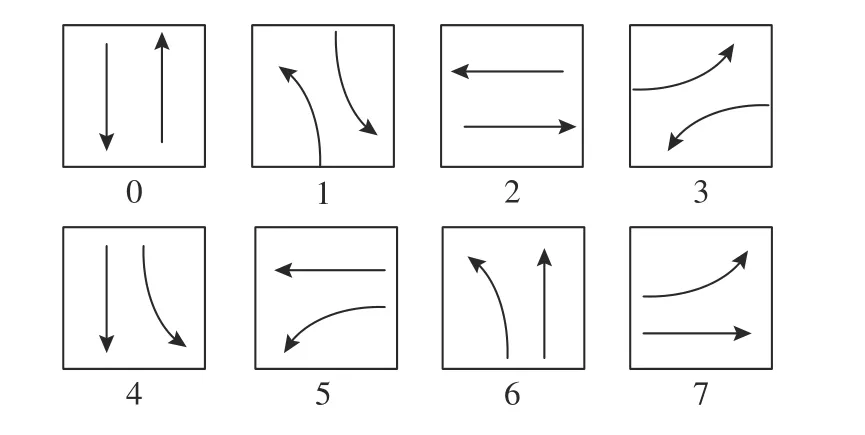
图3 交叉口相位方案集合Fig.3 Combination diagram of intersection phase scheme
1.1.3 奖励函数 传统信号控制领域已总结出较多的交通指标来评价交叉口处车辆的通行效率,比如排队长度、吞吐量、车辆延误等.交叉口信号控制的目标是降低所有通行者的平均旅行时间.在强化学习处理信号控制问题当中,奖励函数一般通过动作执行前后某些指标的变化来给予智能体反馈,比如排队长度的变化[18]、延误时间的差值[13].由于不考虑行人过街,本研究将降低交叉口所有车辆的平均旅行时间作为优化目标.在仿真过程中,车辆的旅行时间无法通过直接测量得到,Zheng 等[17]指出使用交叉口的排队长度作为奖励函数与优化车辆的旅行时间具有较强的相关性,因此本研究使用动作执行前后的排队强度之差 ΔL作为奖励函数的首要指标.考虑到交通量小的方向排队强度一直很小,智能体在选择相位时可能忽略该方向的车辆,导致车流量小的方向单车延误较高,在排队强度指标的基础上加入车辆最大等待时间Wmax,引导智能体更加合理地选择相位.智能体的奖励函数定义式为
式中:k1、k2为每个指标对应的权重系数,取值均为1.
1.2 预训练模型
通过专家数据对模型进行初始化训练以获得性能较好的策略是解决深度强化学习方法学习速度慢的方法之一.Hester 等[19]将人类玩游戏的经验数据与深度强化学习进行融合,提出学习演示的深度 Q 学习(deep Q-learning from demonstrations,DQFD)方法.DQFD 通过离线的方式利用人类的经验数据对DQN 算法中的神经网络进行初始化,缓解了深度强化学习模型初始化不稳定的状况,在一定程度上加快了网络的学习.与DQFD 解决的问题不同,在交通信号控制领域中不存在专家轨迹样本.本研究须解决2 个问题:1)采用何种交通控制方法作为模仿的专家方法,2)如何利用该交通控制方法产生的数据对深度强化学习智能体进行预训练.
Max-Pressure 方法[20]旨在通过最小化交叉口的压力来平衡相邻交叉口之间的排队长度,从而降低过度饱和的风险.在Max-Pressure 方法中,信号灯每间隔固定的时间切换相位,其中相位根据各个相位的压力差从给定的相位方案中选取,相位方案如图3 所示.压力差定义为相位控制的进口车道排队车辆数与相应出口车道排队车辆数的差值.Max-Pressure 方法与本研究设计的智能体动作空间一致,且该方法作为对比方法在以往的强化学习信号控制研究中均表现出较好的控制效果,因此Max-Pressure 方法相比于其他方法更加适合作为本研究中智能体模仿的专家方法.
在选定专家方法后,可以通过仿真实验获取专家方法的经验数据,即形如状态st、动作at、下一时刻的状态st+1、 奖励rt的序列.具体来说,在每次执行Max-Pressure方法选择动作前,先根据状态要素获取交叉口处的st,并储存Max-Pressure 方法给出的at,在下次动作选取之前,获取交叉口处的st+1以及该动作带来的rt.为了使智能体在与环境互动前能够从这些经验中获取较好的先验知识,并将其表现在状态-动作对的Q 值上,引入4 类损失作为预训练阶段损失函数的要素,即1 步Q 学习TD 损失L(θ) ,n步Q 学习TD 损失Ln(θ) ,监督式边际 分 类 损 失LE(θ) 以 及L2正 则 化 损 失L2(θ).采用1 步与n步Q 学习损失混合更新Q 网络有助于将Q 值传递到更早的状态,保证训练的网络满足贝尔曼方程.应用于该网络的权重和偏置的 L2 正则化损失可以防止网络过拟合于相对较小的专家经验数据集.定义监督式边际分类损失为
式 中:a为 智 能 体 在 状 态s所 做 的 动 作;aE为 专 家方法所做的动作;l(a,aE) 为边际函数,当a=aE时,该函数值为0,否则为正值lp.监督式边际分类损失会迫使非专家动作的值至少比专家动作的值低正值lp.引入监督式边际分类损失对于预训练的结果至关重要.因为通过Max-Pressure 方法获取的经验数据比较少,所以许多需要探索的状态-动作对没有包含在经验数据当中.如果仅使用Q 的学习损失来训练网络,会导致网络估计的Q 值不准确.监督式边际分类损失会引导网络将那些在专家经验中从未出现的状态-动作对的Q 值估计成合理的值,使得由价值函数引起的贪婪策略可以模拟专家方法.损失函数定义式为
式中: λ1、 λ2、 λ3为各个损失的权重系数.
1.3 相位持续时间计算
深度强化学习智能体执行动作的频率一般固定在1.0、0.2、0.1 Hz.高频的动作不但不利于网络的收敛,而且容易造成信号的反复切换导致黄灯时长增加.低频的动作不利于信号的灵活切换,使得智能体的控制达不到最优的控制效果.因此执行动作的频率对于网络的收敛以及智能体的控制效果尤为重要,最佳的智能体应能通过使用较少的动作达到最优的控制效果.本研究引入平均车头时距计算动作的持续时间,使得每次相位的绿灯时间能够与交叉口处交通流的实时状态联系在一起.具体而言,智能体先根据状态特征计算出最佳的信号相位,在执行该相位前通过交叉口处的检测器检测该相位控制的车道内排队车辆的数量,该相位的持续时间计算式为
式中:tmin为最小绿灯时长,tmax为最大绿灯时长,tloss为头车的启动损失时间,h为交叉口处释放车流的平均车头时距,Nveh为相位控制车道内最大排队车辆数.如果排队长度过长,导致计算的相位绿灯时间超过最大绿灯时长,则强制设置动作的持续时间为最大绿灯时长;如果排队长度过短,导致计算的相位绿灯时间小于最小绿灯时长,则设置动作的持续时间为最小绿灯时长.这一规则,既减少了绿灯空放造成的时间损失,也避免了因为动作频率过高导致的黄灯损失.该规则也在一定程度上降低了交叉口处交通控制的复杂性,智能体可以将该规则视为环境的一部分,从而帮助智能体学习.
1.4 交通信号控制强化学习算法
结合状态、动作的定义,采用3DQN 算法作为控制交叉口信号灯的智能体.3DQN 算法的核心是深度神经网络,它可以从状态空间中提取特征并将这些特征映射到Q 值函数上.智能体可以根据Q 值函数来选择最优的行动,实现有效的学习.3DQN 算法相比于DQN 算法加入Dueling Network结构与Double Network 结构.Dueling Network改善了DQN 算法的估计效率,它将Q 值函数分解为2 个部分:用于估计状态价值的值函数,用于估计动作价值的动作函数.Double Network 缓解了DQN 算法对Q 值估计过高的问题,在Double Network中,存在动作网络和目标网络.这2 种网络的初始化参数一致,但更新方式不一致,动作网络通过梯度下降直接更新参数,目标网络采用软更新的方式更新参数.
为了平衡探索与利用的关系,采用动态贪婪策略训练模型.动态贪婪策略在训练过程中动态改 变 贪 婪 系 数 ε 的 大 小.训 练 开 始 时 ε 的 值 比 较大,智能体倾向于选取随机动作进行前期的探索过程.随着训练时间的增加, ε 的值逐渐减小,智能体更倾向于选取对应Q 值最大的动作.本研究的模型框架如图4 所示.1)通过使用Max-Pressure方法控制信号灯完成整个仿真实验.在该过程中收集Max-Pressure 方法的经验序列.2)使用收集到的经验序列通过预训练对3DQN 算法中的深度神经网络进行初始化,使得3DQN 算法中的深度神经网络既能够满足贝尔曼方程,又能够模仿Max-Pressure 方法选择动作的策略.3)经过初始化后的智能体将与环境进行实时交互,并将获取的经验存放于经验缓冲池中,满足更新条件时则从经验缓冲池中取出小批量的样本进行学习,经过反复迭代最终网络达到收敛.
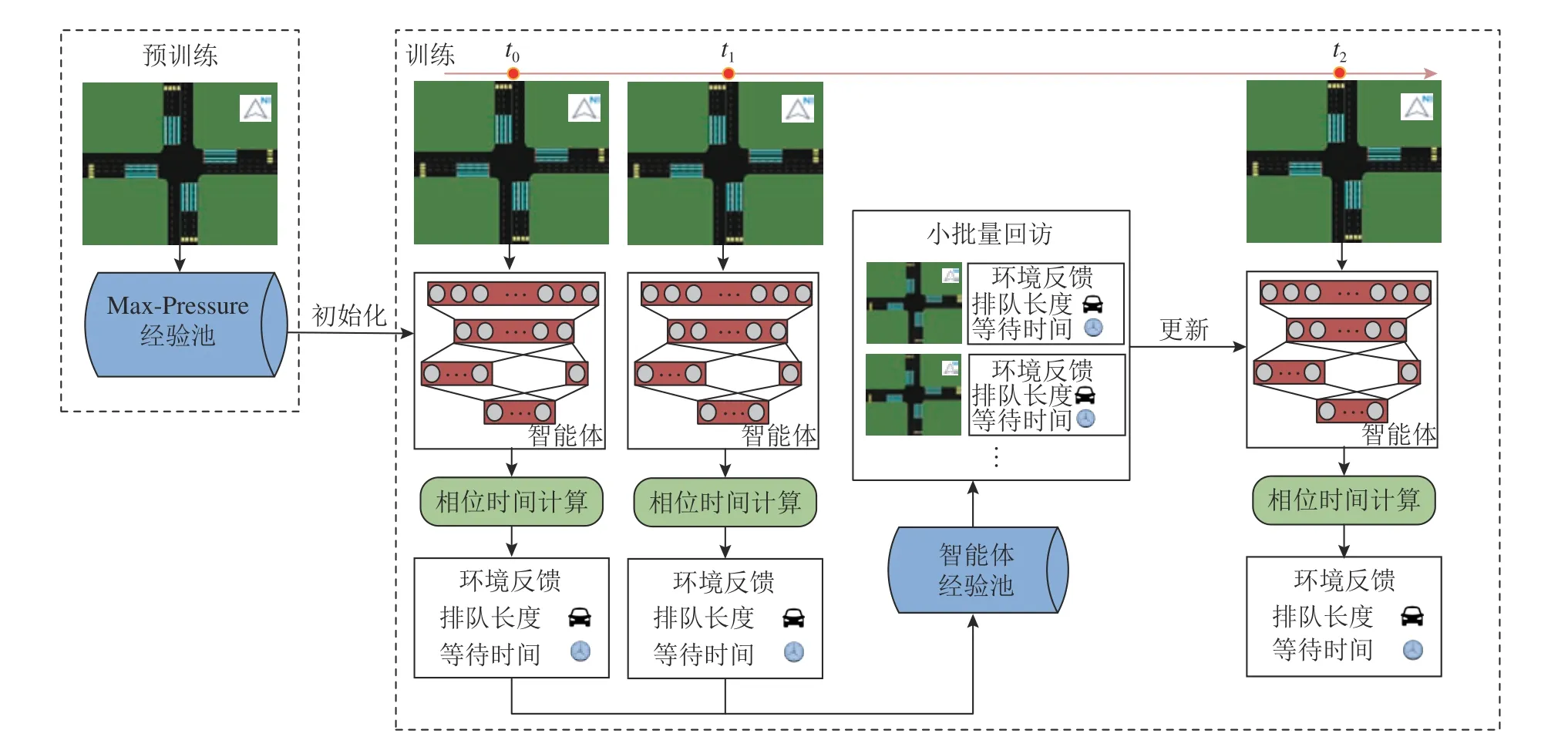
图4 基于双决斗深度Q 网络的信号控制模型框架Fig.4 Signal control model framework based on double-dueling deep Q network
在3DQN 算法中,超参数的设计对训练结果有重要影响.本研究算法的参数具体如下:深度神经网络的激活函数为ReLU,梯度下降算法为Adam,学习率为0.001,经验缓冲池的容量设置为10 000,折扣因子为0.99,贪婪系数初始值为1,贪婪系数衰减率为0.95,最小贪婪系数为0.005,目标网络软更新系数为0.005,小批量经验大小为256.在 预 训 练 阶 段, λ1=0.1, λ2=1, λ3=1.0×10-5,n=5,lp=0.8.
2 案例分析与实验结果
2.1 案例分析与实验配置
杭州市萧山区机场城市大道与博奥路交叉口是典型的四岔路口,东西南北方向各有4 个进口道和3 个出口道,其中东西方向为1 条直右车道、2 条直行车道和1 条专用左转车道,南北方向为1 条专用右转车道、2 条直行车道和1 条专用左转车道,东西南北方向的进口道长度分别为500、450、450 和300 m.本实验收集2021 年10 月18 日至2021 年10 月24 日一周的流量数据.2021 年10 月18 日原始数据每15 min 进行一次统计,得到的流量分布如图5 所示,N为车辆数.针对早高峰时段(8:30—9:30)的交通情况开展本次实验研究,该时间段内过车车辆类型的统计结果如表1 所示,其中P为车辆占比.仿真过程采用7 种车辆类型,车辆类型设置如表2 所示,其中L为车身长度;D为速度因子分布,是车辆的最大行驶速度与道路限速的比值,车辆速度因子分布用以模仿不同的驾驶行为(如激进驾驶、保守驾驶).每种车辆类型的速度因子从截断正态分布Normc中取出,截断正态分布Normc 中含有四类参数,依次代表截断正态分布的均值、标准差、最小截断速度与道路限速的比值、最大截断速度与道路限速的比值.仿真实验中的其他实验参数设置如下: 道路规定上限速度为13.89 m/s,车头最小间距为2.5 m,最小绿灯时间为5 s,最大绿灯时间为50 s,黄灯时间为3 s.一次仿真时长为3 600 s,在仿真初始的0~50 s 为加载路网车辆,信号灯依据Webster 配时方案进行信号控制.
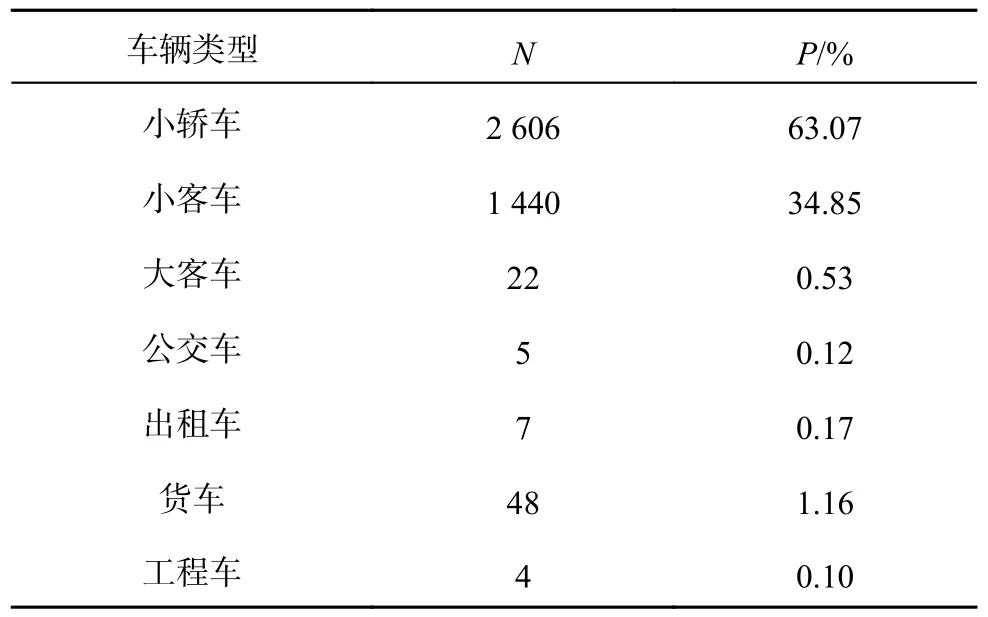
表1 高峰时期交叉口过车车辆类型分布Tab.1 Distribution of passing vehicle types at intersections during peak hours
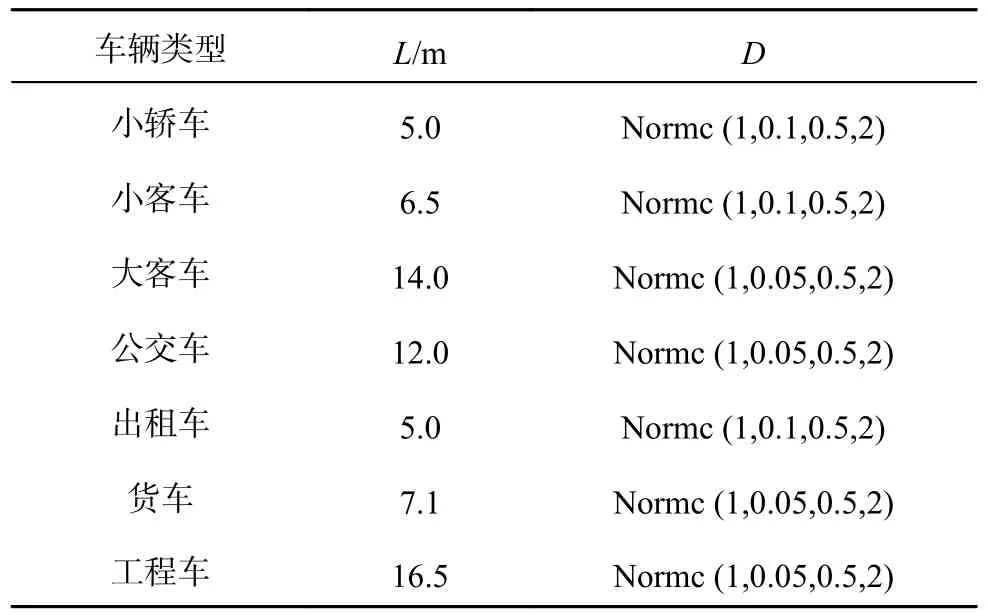
表2 仿真实验车辆类型设置Tab.2 Simulation experiment vehicle type setting
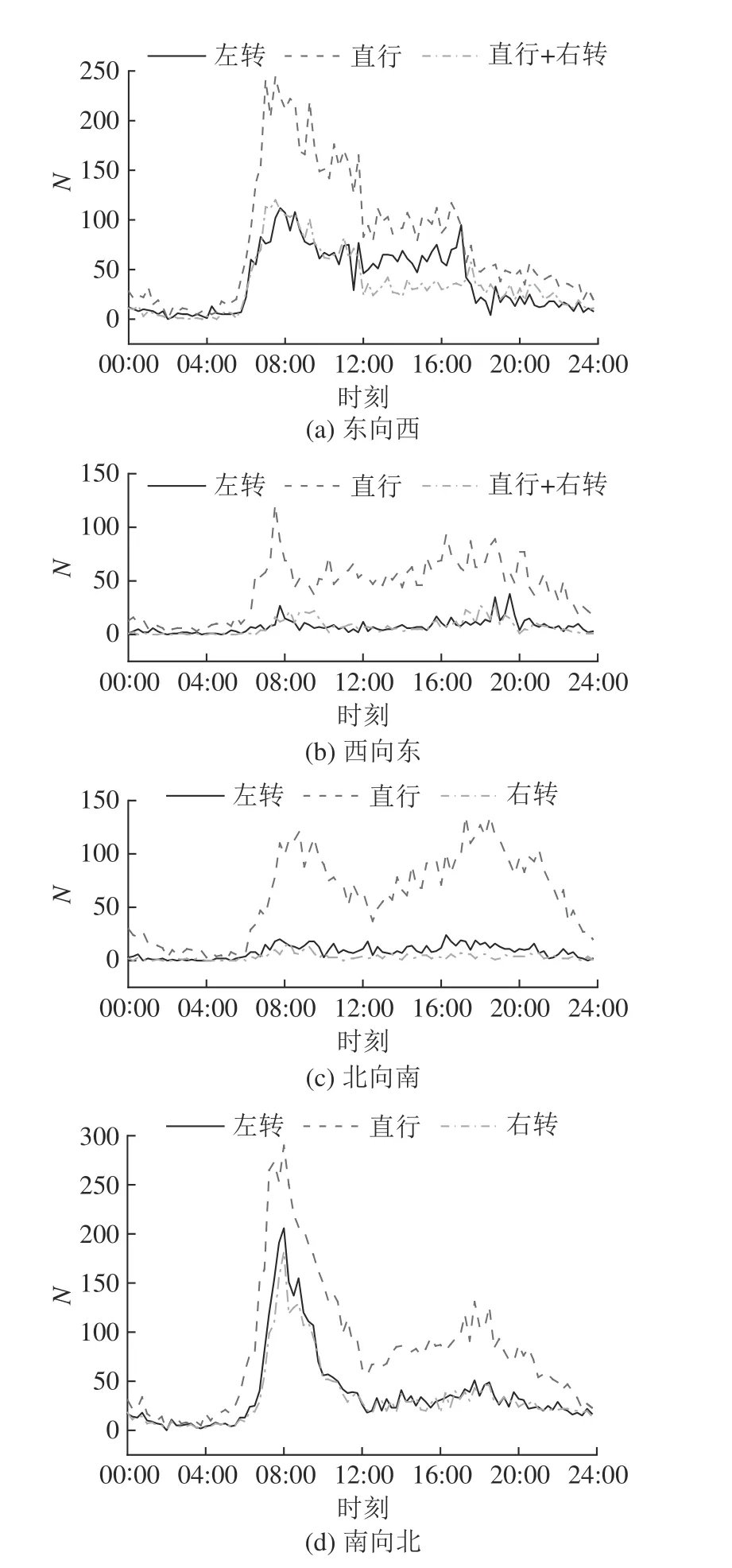
图5 交叉口全天的流量分布图Fig.5 Flow distribution diagram of intersections throughout day
2.2 实验结果与分析
利用2021 年10 月18 日的早高峰数据进行仿真训练,与传统的基于3DQN 算法、感应式信号控制方法Actuated 和Delay-Based[21]以及定时信号控制方法Webster 的控制效果进行对比.不同方法在车辆平均等待时间tw、 平均旅行时间tt和车辆平均速度v上的控制效果如表3 所示.本研究算法在各项指标上均表现出最好的控制效果.相比于定时信号控制,本研究算法在平均旅行时间上减少了22.97%.如表4 所示为采用不同方法控制信号灯时各进口道的平均排队长度,其中Ln、Ls、Le和Lw分别为北进口道、南进口道、东进口道和西进口道的排队长度.可以看出,本研究所提算法相比于其他控制方法能够明显缩短东进口道和南进口道的排队长度.如图6 所示为采用不同方法控制信号灯时路网内车辆平均等待时间的变化情况,其中t为仿真时刻.可以看出,本研究算法相比于其他方法,在车辆平均等待时间上波动更加平稳.
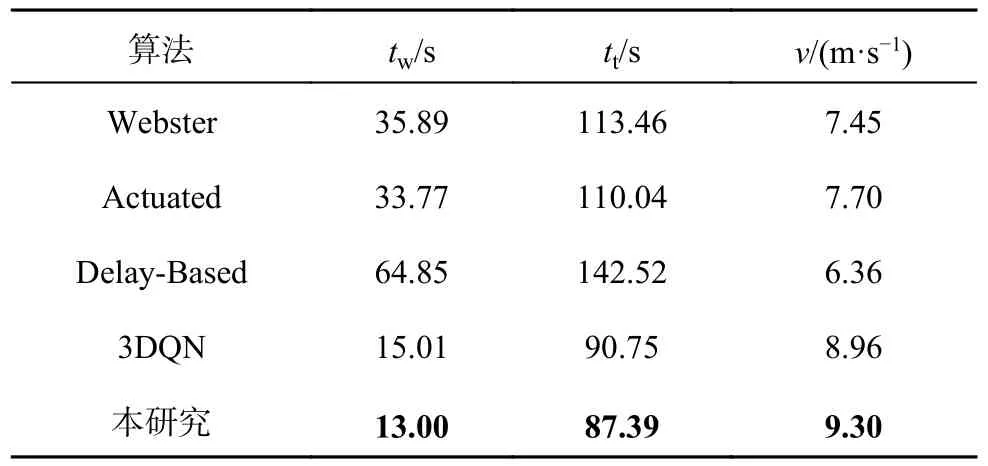
表3 不同方法的控制效果对比Tab.3 Comparison of control effects among different methods
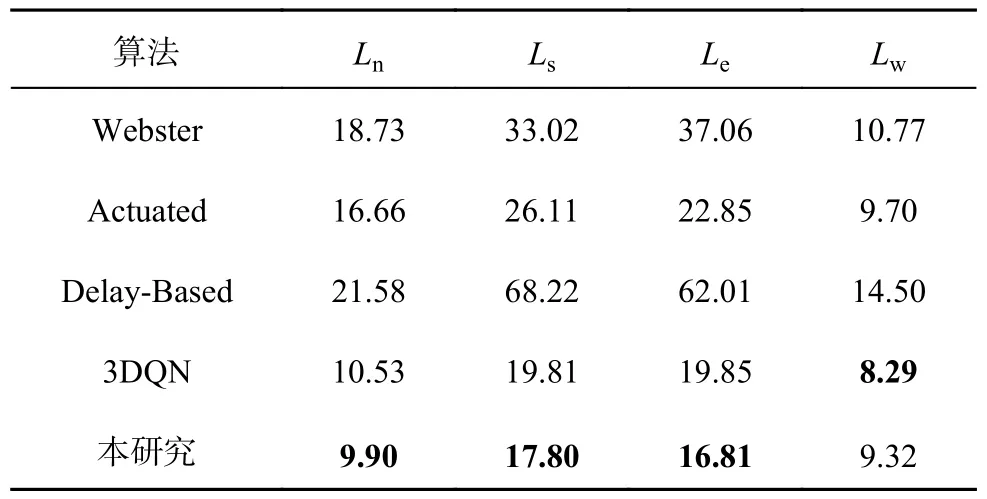
表4 不同方法下各进口道的平均排队长度Tab.4 Average queue length of each approach under different methodsm
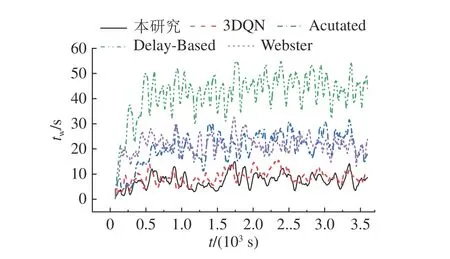
图6 不同方法下路网内车辆平均等待时间变化Fig.6 Variation of average waiting time for vehicles in road network under different methods
为了进一步探究所提方法的性能,选取2021 年10 月18 日 至2021 年10 月24 日 一 周 的 早高峰数据对训练好的模型进行测试,实验结果如图7 所示.可以看出,相比于其他信号控制方法,本研究算法在一周的测试中均表现最佳.
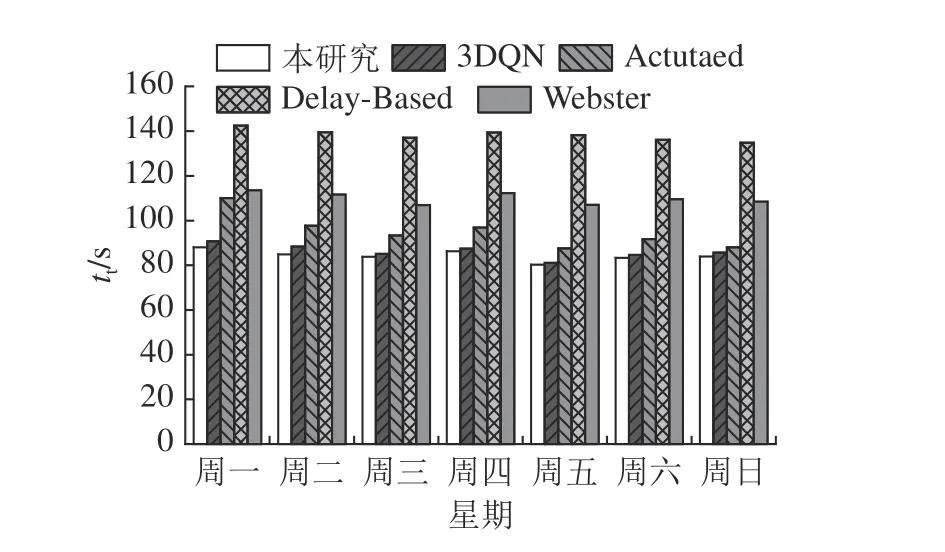
图7 不同方法下早高峰时段一周的平均旅行时间变化Fig.7 Average travel time during morning peak hours for one week under different methods
2.3 方法改进效果验证
为了探究预训练模块以及相位持续时间模块对于收敛速度和控制效果的影响,在不改变其他参数的情况下,分别将加入预训练模块的方法和加入相位持续时间模块的方法与传统3DQN 算法在收敛速度和平均旅行时间控制效果上比较.加入预训练模块的3DQN 算法与传统3DQN 算法对比结果如图8 所示,R为训练过程中智能体在一次仿真过程获得的总奖励,E为仿真迭代次数.可以看出,使用Max-Pressure 方法的经验数据对模型进行初始化能够稳定模型的学习过程,减少前期的波动,同时通过预训练可以帮助智能体更快地达到收敛.产生此种结果的原因在于模型在探索期间使用的动态贪婪策略.当探索系数 ε 逐渐变低时,信号灯的相位将由模型产生的Q 值决定.相比于未预训练的网络,经过预训练后的网络在训练初期能够以更高的概率选择专家动作.
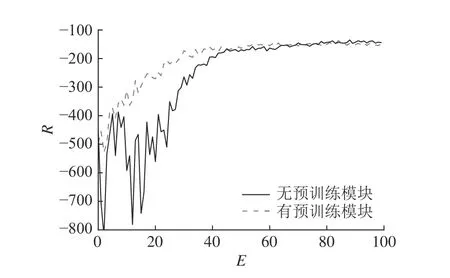
图8 加入预训练模块与未加入预训练模块的双决斗深度Q 网络算法收敛速度情况Fig.8 Convergence speed comparison of double-dueling deep Q network algorithms with and without pretrained module
如图9 所示为加入相位持续时间模块的3DQN 方法(3DQN-DT) 与动作间隔为10 s 的3DQN 方法(3DQN-10)、动作间隔为5 s 的3DQN 方法(3DQN-5)在平均旅行时间指标上的收敛情况.可以看出,3 种不同设置的模型在收敛速度上较为一致,但3DQN-DT 在最终收敛结果上超过了3DQN-10 和3DQN-5,其中3DQN-DT 的平均旅行时间为87 s,3DQN-10 的平均旅行时间为90 s,3DQN-5 的平均旅行时间为105 s.
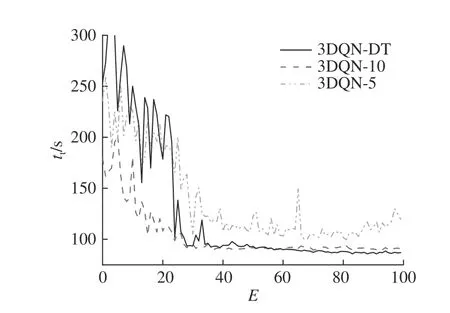
图9 加入相位持续时间模块的双决斗深度Q 网络(3DQN)算法与传统3DQN 算法在平均旅行时间上的收敛情况Fig.9 Convergence analysis of double-dueling deep Q network(3DQN) algorithms with phase duration module and traditional 3DQN algorithm on average travel time
为了进一步探究3DQN-DT 方法与3DQN-10、3DQN-5 的差异,就模型的选择策略、各个相位在仿真过程中的总绿灯时长进行分析.如图10 所示为3 种方法在选择策略上的分布情况.图中,x为动作选择的相位,其中x=1 代表动作选择的是排队长度最大的相位,x=2 代表动作选择的是排队长度次大的相位,y为智能体选择某种相位的次数,PN为智能体选择某种相位的次数占总选择次数的比例.3DQN-DT 共执行307 次动作,其中60.26% 的动作选择了排队长度最大的相位;3DQN-10 共执行280 次动作,其中64.64%的动作选择了排队长度最大的相位;3DQN-5 共执行463 次动作,其中56.59%的动作选择了排队长度最大的相位.3 种模型在选择策略上的变化趋势较为一致,因此相位持续时间模块对模型的动作选择策略影响较小.如图11 所示为3 种模型在相位绿灯时间上的分布情况,其中Ph为动作空间中的8 种相位,tg为绿灯时间.在所有相位的总绿灯时长上,3DQN-DT 的绿灯时间为2 744 s,3DQN-10的绿灯时间为2 800 s,3DQN-5 的绿灯时间为2 315 s.可以看出,3DQN-5 由于动作时间间隔的缩短导致相位交替过快,仿真过程中造成的黄灯损失较多,因此该模型的控制效果不如其他2 个模型.3DQN-10 的绿灯时间最长,但其控制效果却不如3DQN-DT,原因在于3DQN-DT能够根据车道内排队情况动态调整相位的绿灯持续时间减少绿灯空放情况的发生.还可以看出,3DQN-DT 将更多的绿灯时间分配给了相位5 和相位6.周一的交通流数据显示该交叉口存在明显的南北交通流不均衡以及东西交通流不均衡的情况,因此采用单向放行的相位相比于对向放行的相位更能够提高交通流的运行效率,减少车辆的平均延误.此外,3DQN-DT 通过检测交通流对绿灯时间分配进行了进一步的优化,提高了路网交通流的运行效率.
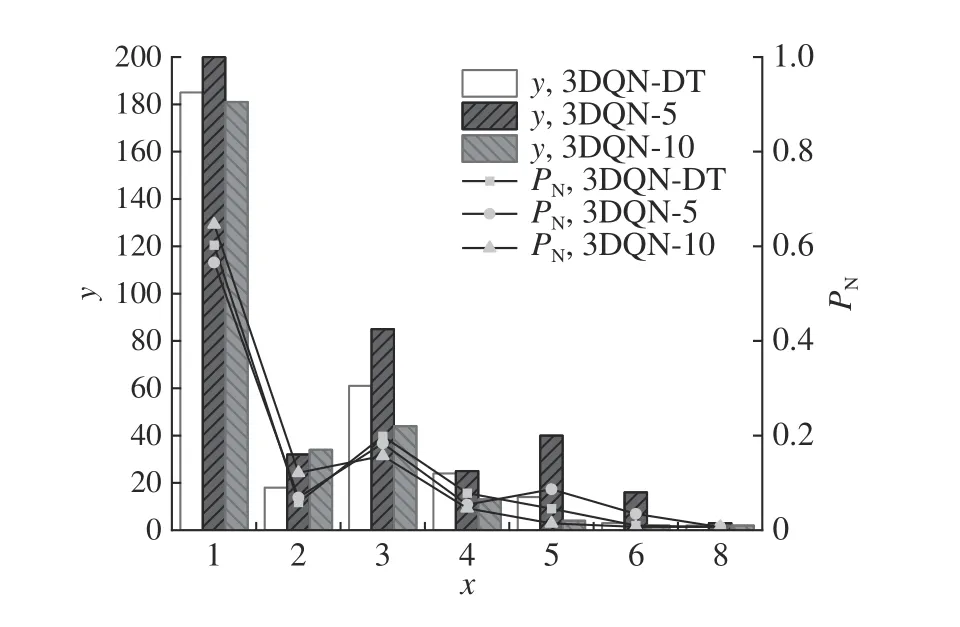
图10 不同间隔时间设置下的模型动作策略示意图Fig.10 Schematic diagram of model action strategy under different intervals settings
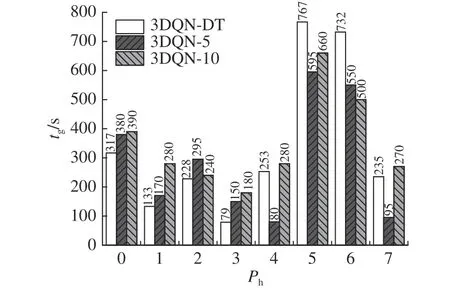
图11 不同双决斗深度Q 网络算法的各相位绿灯总时长对比图Fig.11 Comparison diagram of total green light duration for each phase with different double-dueling deep Q network algorithms
3 结 语
基于深度强化学习方法对单交叉口进行信号控制已经有了长足的发展,以往研究从状态表达、动作设计等不同的角度出发探寻并挖掘了深度强化学习方法在信号控制领域的潜力.本研究提出使用Max-Pressure 方法预先初始化3DQN 算法中神经网络的参数,使得预训练后的3DQN 算法能够在满足贝尔曼方程的基础上模仿Max-Pressure 的策略.针对3DQN 算法存在的动作执行频率过高或过低的问题,本研究引入平均车头时距动态计算每次相位的绿灯持续时间,保证了排队车流释放的顺畅性,减少了绿灯损失.根据真实的交叉口流量数据对所提算法进行验证,结果表明本研究算法能够有效解决现有方法在训练过程中存在不稳定、迭代慢的问题.相比于传统的信号控制方法和感应控制方法,本研究算法能够显著提高交叉口处的运行效率.本研究仅限于单交叉口的信号控制问题,未讨论目标交叉口策略的改变对于邻近交叉口的影响.在城市交通中,交叉口之间的相互关联作用与交叉口之间的距离和交通流量有着密切的关系.通过深度强化学习方法对多个交叉口形成的干线网络或区域网络进行协调控制,并分析流量与距离对协调控制的影响将是下一步研究的重点.

