综合上下行链路的无线能量收集协作网络资源分配

周欣彤，肖琨

(广西师范大学 电子与信息工程学院，广西 桂林 541004)

随着移动通信技术的发展，能量消耗和频谱资源问题日益严重[1].能量收集(energy harvesting,EH) 技术从可再生能源中获取能量以驱动通信设备和网络，降低了系统对电网的依赖[2].资源分配是无线通信网络提升效能的关键技术，通过调整节点发射功率和频谱分配可以有效提高系统的频带利用率和能量利用率[3-5].

在无线EH 协作网络资源分配领域，Han 等[6]针对时变能量收集驱动的水下传感器网络，提出基于分层的深度强化学习框架，通过中继选择和功率分配的联合优化，提升上行链路的累积性能.Zhuang 等[7]在环境反向散射通信中提出混合同步信息和能量传输(simultaneous wireless information and power transfer, SWIPT)辅助中继传输方案，利用拉格朗日对偶理论和次梯度推导得到基于功率分配和时间分配的联合优化迭代算法，最大化反向散射通信的吞吐量.Gu 等[8]研究非线性EH 下两跳多中继网络的吞吐量最大化问题，采用逻辑函数模型和常线性常数模型表征非线性，优化源-中继链路的传输功率和带宽的联合分配以及中继的功率分割(power splitting, PS)比.Liu 等[9]研究基于SWIPT 的全双工放大转发(amplify-andforward, AF)多中继系统的资源分配问题，提出基于可证明收敛博弈论的分布式迭代注水算法；该算法在发射功率和能量收集约束下，最大限度提高了干扰信道的总速率.Euttamaraja 等[10]针对采用解码转发策略的两跳SWIPT 中继网络,提出基于椭球方法的迭代原对偶算法，推导源和中继功率分配以及PS 的最优解析表达式，提高了端到端的可实现速率.Xu 等[11]研究具有窃听者的EH 协作中继网络的功率分配问题，提出基于凸函数差分规划的迭代算法；该算法在保证信息安全传输的同时达到了较高的可实现保密速率.Liu 等[12]考虑基于时频块分配的EH 中继网络的通信场景，以提高下行链路传输速率和降低功耗为目标，将时频块配对算法和块功率分配算法相结合.Chen 等[13]研究混合能量收集的设备到设备(device to device, D2D)辅助边缘计算系统中的资源分配策略，采用量子粒子群优化算法得到次优解；该策略在计算延迟和能量收集的约束下最大限度地提高了系统能效.Salim 等[14]针对中继辅助D2D 的下行链路频谱共享的网络，提出低复杂度的EH 辅助中继选择的资源和功率分配算法，该算法能够有效提高系统网络的频效和能效.Ojo 等[15]研究射频(radio frequency, RF)供电的协作中继网络的最优功率分配问题，提出基于迭代节能算法的节能时间交换中继和节能功率分割中继协议，实现能量效率的最优化.Xu 等[16]利用非线性EH 研究不可信中继的节能安全通信，提出基于优化解耦、分数规划、拉格朗日对偶分解和凸函数差规划的双层算法，所提算法通过优化分段区域选择和功率分配提高能量利用率.

上述工作在开展时，很少考虑上行链路和下行链路的关联性.在上下行链路共享频谱的情况中，信道特性存在差异，综合上下行链路的研究有助于掌握系统的全面性能.同时，EH 是解决无线通信设备能量短缺问题的有效技术[17-19]，无线协作网络不但能扩大小区覆盖，而且能有效节约能量.为了提高系统能效，将在无线EH 协作网络中开展综合上下行链路的资源分配算法研究：1）通过联合优化带宽和功率分配，平衡上行和下行链路之间的能效，建立多中继节点的上下行链路频谱共享的系统模型，以最大化绿色能效和传统能效为目标；2）利用Dinkelbach 方法对优化问题进行转化，通过KKT 分析，求得节能资源分配的最优解，包括最优的发射功率、上下行链路最优的带宽分配、最优的功率分割以及最优的系统能效；3）归纳节能资源分配算法，对算法进行仿真对比，验证算法的有效性.

1 系统模型

无线EH 协作网络模型如图1 所示，模型包含源节点（source node，SN）、S个能量收集型中继节点(relay node，RN)以及S个目的节点(destination node，DN).假设每个中继节点接入1 个目的节点，通过收集无线能量提供自身电力驱动，且中继为时分双工中继，采用解码转发(decode and forward，DF)协议进行传输.由于SWIPT-PS 技术收集能量的稳定性适用线性的能量收集模型[20]，也为了方便数学分析，本研究采用线性能量收集模型.

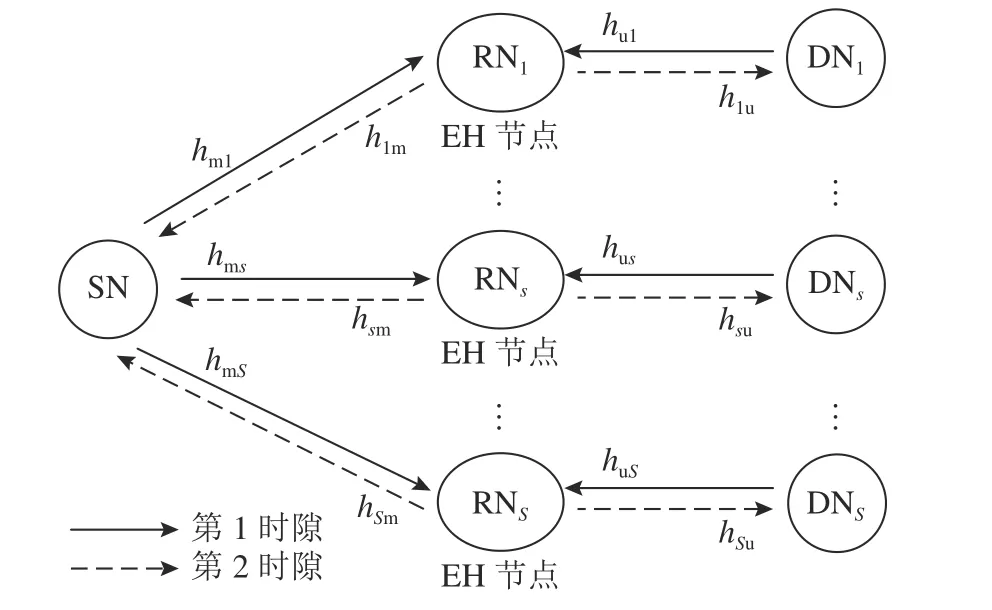
图1 能量收集协作中继网络Fig.1 Energy harvesting cooperative relay network

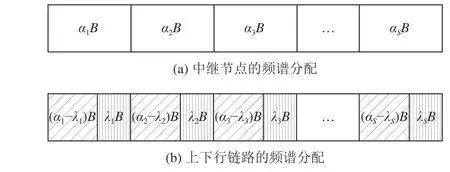
图2 多中继上下行链路的频谱划分Fig.2 Spectrum division of multi-relay uplink and downlink

第1 时隙，SN 向第s个RN 发送信号，SN 到第s个RN 的下行链路传输速率为

式中：hms为SN 与第s个RN 之间下行链路的信道增益，no为噪声功率谱密度.同一时隙，DN 向第s个RN 传输信息，DN 到第s个RN 的上行链路传输速率为

式中：hus为DN 与第s个RN 之间上行链路的信道增益.

第2 时隙，RN 利用上一时隙收集到的能量向DN 发送信息，第s个RN 到DN 的下行链路传输速率为

式中：hsu为第s个RN 与DN 之间下行链路的信道增益；Ps为第s个RN 的下行发射功率，

式 中： ε 为 能 量 转 换 效 率，0 <ε ≤1.同 一 时 隙，RN 向SN 发送信号，第s个RN 到SN 的上行链路传输速率为

式中：hsm为第s个RN 与SN 之间上行链路的信道增益，Ps′ 为第s个RN 的上行发射功率，有

上行传输中的可实现速率受DN 到RN 上行链路速率和RN 到SN 上行链路速率的限制，下行传输中的可实现速率受SN 到RN 下行链路速率和RN 到DN 下行链路速率的限制，因此引入变量Rths为下行最小可实现速率，变量Rrhs′为上行最小可实现速率，

由于上下行链路的非对称特性，假设系统须保证下行可实现速率至少为上行可实现速率的 γ 倍，即Rths≥γRrhs′.

2 优化问题

2.1 绿色能效最大化的优化问题

如果重点关注系统收集能量的使用效率，则定义系统综合上下行传输的绿色能效为

为了便于衡量系统的能效性能，假设系统中源节点和∑目的节点∑的发射功率之和小于或等于P，即.在此基础上，形成最大化系统绿色能效的优化问题P1：

式中：Rmin为下行最小可实现速率；条件C1 约束下行可实现速率至少为上行可实现速率的 γ 倍，限制了最小可实现速率；条件C2 约束源节点和目的节点的发射功率之和的上界；条件C3 约束中继链路的总带宽；条件C4 约束上下行带宽的分配；条件C5、C6 约束能量收集的功率分割因子.通过求解优化问题P1，可以获得节点（包括最优的源节点、中继节点和目的节点）的发射功率、最优的带宽分配以及最优的功率分割.

2.2 系统能效最大化的优化问题

如系统模型所述，中继节点通过收集来自源节点和目的节点的信号能量供电，因此系统消耗的能量仅包括源节点和目的节点的能耗，为了方便推导且不影响结论，不考虑节点的电子器件功耗，只考虑空口的功耗，将系统功耗表示为

此时，定义系统综合上下行传输的能效为

在此基础上，形成最大化系统能效的优化问题P2：

P2 的约束条件与P1 的相同.通过求解优化问题P2，可以获得节点（包括最优的源节点、中继节点和目的节点）的发射功率、最优的带宽分配以及最优的功率分割.

3 优化问题求解

3.1 优化问题P1 的求解

P1 是非线性分式规划问题，为此，定义系统最大绿色能效为

定理1：系统的最大能效当且仅当

成立时得到[21].由于优化问题 P1 的目标函数难以直接求解，受定理1 启发，引入参数φ将该优化问题的分式形式转化为减法形式：

P3 是多变量耦合的优化问题，假设每单位载频的发射功率是恒定的[22]，则SN 到第s个RN 的发射功率满足∀s∈Γ，条件C2 可以转化为C2'：Pms≤λsP,∀s∈Γ.条件C2包含的原始可行性条件为

P3 的拉格朗日函数(Karush-Kuhn-Tucker, KKT)条件具有最优性，根据问题P3 及原始可行性条件，引入拉格朗日乘子，将不等式约束条件转化为等式约束条件，即将离散的问题转化为连续的凸优化问题，构建多变量拉格朗日函数为

由 K 11 可以得到

由 K 12 可以得到

将 K 3 代入(18)得到

联合式(17)、(19)得到

将式(16)代入式(20)，得到下行最优功率分割因子：

联合 K 4 和 式(22)得到第s个RN 的最优带宽分配为

将所求资源分配最优解代入式(12)得到最优能效值：

3.2 优 化 问 题P2 的 求 解

P4 是多变量耦合的优化问题，由优化问题P1 的求解可知Pms=λsP,Pus=(αs-λs)P,∀s∈Γ ，故约束条件C2 转化为

继续使用求解优化问题P1 的证明方法，结合约束条件C2″和K1～K4，构建拉格朗日函数，分别对 α 、λ、 τ 、Rths、Ps求偏导，得到拉格朗日平稳性条件，列出对偶可行性条件.通过讨论互补松弛条件中拉格朗日乘子 βs1、βs2的4 种松弛情况，得到结论：当 βs1>0, βs2>0时 ，满足所有KKT 条件.同理，可以求得信息解码和能量收集的功率分割最优解，下行频谱分配最优解以及第s个RN的最优频谱分配，将求得的最优解代入式(11)得到最优能效值：

4 综合上下行链路的资源分配算法

优化问题的数学推导，可以归纳得到基于绿色能效最大化的资源分配算法步骤如下.

4)一次协作传输完成.

基于能效最大化的资源分配算法与基于绿色能效最大化的资源分配算法具有相似的步骤，区别仅在于推导的参数表达式不同，因此只需要更换相应参数的计算公式即可.

5 仿真分析

通过Matlab 对本研究提出的绿色能效最大化资源分配算法HEEM-RAA 和能效最大化资源分配算法EEM-RAA 进行仿真验证，并与基于时频块分配的资源分配算法[12]TFB-RAA、双向中继资源分配算法[23]DDR-RAA 进行对比，Han 等[23]考虑双向AF 中继辅助的通信场景，综合频谱共享、速率限制、双向功率控制等特征，提出双向资源分配方案.在仿真过程中，仿真模型包括1 个源节点、若干个中继节点和目的节点，SN 与RN 之间的信道以及RN 与DN 之间的信道均为瑞利平坦衰落信道，系统总带宽B=20 MHz.假设能量转换效 率 为理 想 状态，即 ε =1 ，中继 节 点个 数S=8 ，SN 和DN 的总发射功率限制为Pmax=20 W ，下行最小可实现速率Rmin=10 Mbit/s ，下行可实现速率为上行可实现速率的2 倍，即 γ =2.

如图3 所示为在不同的中继个数下，系统的绿色能效随总功率发射限制的变化情况.可以看出，随着总功率的增加，绿色能效降低并趋于平稳.随着总发射功率持续增加，尽管信道容量增加，但各节点的功耗越来越大，绿色能效降低.在同等条件下，HEEM-RAA 优化中继节点的绿色能效，有效降低系统消耗，因此绿色能效较优.当总功率小于一定值时，EEM-RAA 的总能效小于DDR-RAA.原因是在总功率较小时，EEM-RAA 分割给信息解码的能量较少，上下行链路的和速率较低，随着总功率增加，EEM-RAA 收集的能量增加，功耗得到补偿，此时能效大于DDR-RAA 的传统能效.

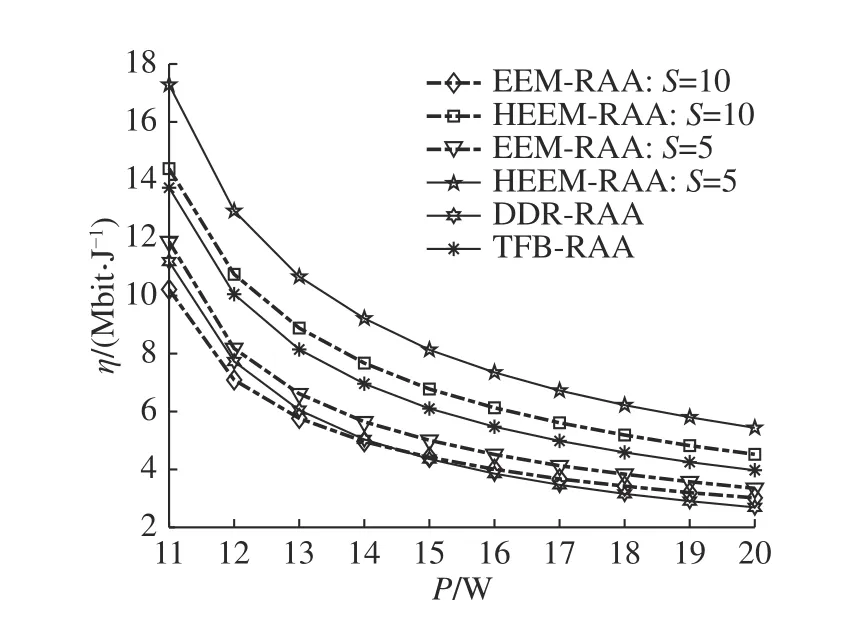
图3 不同算法的系统能量效率和总功耗的关系Fig.3 Relationship between system energy efficiency and total power of different algorithms

如图4 所示为系统的绿色能效在不同功率分割因子 τ 下随带宽分配系数 λ 的变化曲线.仿真结果表明，随着 λ 增大，系统的绿色能效提高并趋于平稳.当 λ 增加时，SN 到RN 下行链路速率提高，RN 收集到的能量增加，RN 到DN 速率随之提高，根据本研究算法上行链路可实现速率也同时提高，因此绿色能效增加.可以观察到，当 λ ≤0.2 时，EEM-RAA 和HEEM-RAA 的能效几乎重合，随着λ增大，HEEM-RAA 的绿色能源使用效率逐渐优于EEM-RAA 的能效，因此绿色能效优于EEMRAA 的总能效；DDR-RAA 对各RN 节点功率进行分配，有效提高了网络能效，但不能对功耗进行补偿，因此其传统能效逐渐低于TFB-RAA.还可以发现， τ 对系统能效也具有影响，当 λ 固定时，随着τ增加，能效得到提升.

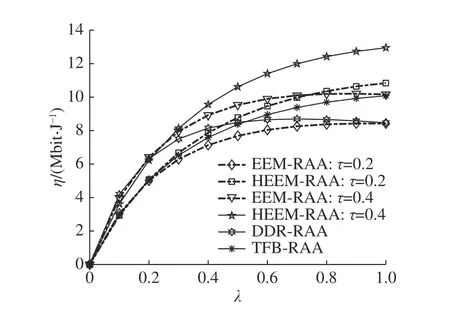
图4 系统能量效率和带宽分配系数的关系Fig.4 Relationship between system energy efficiency and bandwidth allocation coefficient

如图5 所示为在不同的功率分割因子 τ 下，系统能效随中继数量的变化关系.可以看出，随着中继数量的增加，各算法的能效呈下降趋势.中继数量增加，对能量的需求增大，而总发射功率有限，因此能效下降.在同等条件下，EEM-RAA、HEEM-RAA 和TFB-RAA 的中继具有能量收集能力，DDR-RAA 对多中继进行功率分配，未对上下行链路的带宽分配进行优化，因此能效低于其他算法.此外，HEEM-RAA 对收集能量的使用效率进行优化，因此绿色能效下降的趋势较缓慢，优于EEM-RAA 的总能效.

图5 不同算法的系统能量效率和中继数量的关系Fig.5 Relationship between system energy efficiency and numbers of relay node of different algorithms

如图6 所示为系统的绿色能效与上下行速率比 值 γ 在 不 同 功 率 分 割 因 子 τ 下 的 关 系.仿 真 结 果表明，随着速率比值 γ 增大，绿色能效增大.γ 的提高使得共享频谱中用于下行链路的带宽 λs增大，下行传输的最小可实现速率随之增大，上下行链路的和速率提升，因此绿色能效逐渐提高.在同等条件下，HEEM-RAA 考虑收集能量的使用效率，因此绿色能效性能优于EEM-RAA、TFB-RAA的总能效和DDR-RAA 的传统能效.

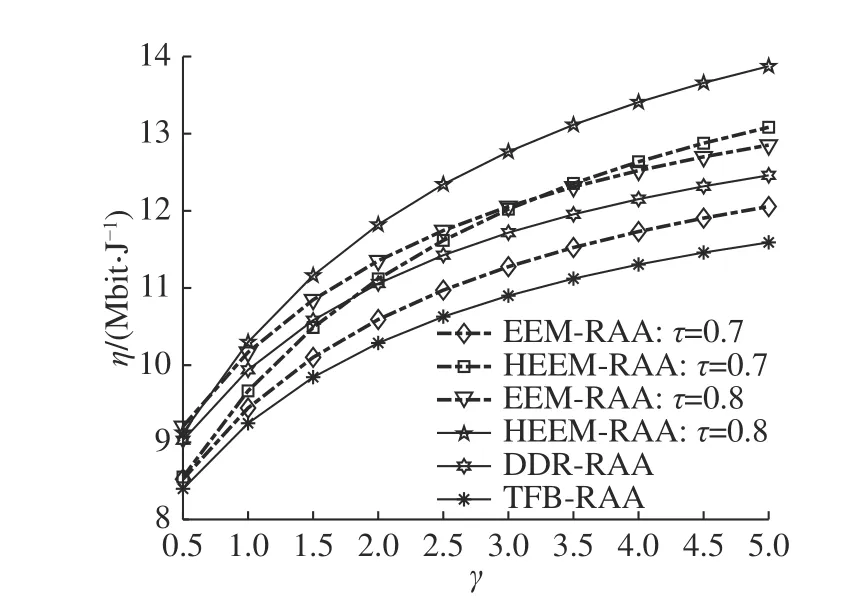
图6 不同算法的系统能量效率和上下行链路速率比值的关系Fig.6 Relationship between system energy efficiency and rate ratio of downlink to uplink of different algorithms

如图7 所示为系统的绿色能效随平均信道增益的变化曲线.仿真结果表明，随着平均信道增益增大，系统的绿色能效得到提高.原因是信道增益影响上行与下行链路的最小可实现速率.在同等条件下，HEEM-RAA 的能耗得到优化，小于EEM-RAA 的功耗，绿色能效优于EEM-RAA，DDR-RAA 没有采用能量收集，因此绿色能效为0.还可以发现，当信道增益固定时，随着 γ 增加，能效也随之提高.

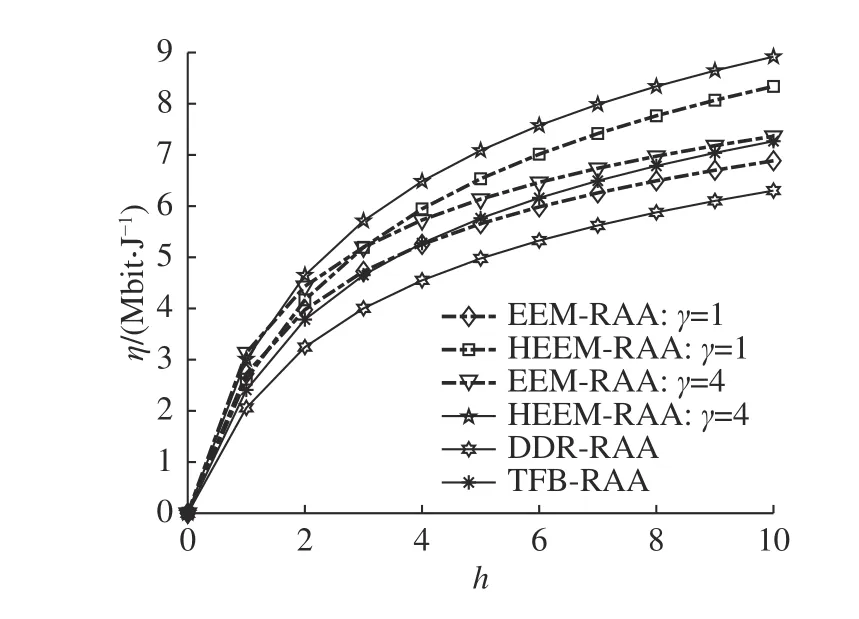
图7 不同算法的系统能量效率和平均信道增益的关系Fig.7 Relationship between system energy efficiency and average channel gain of different algorithms

6 结 语

本研究针对无线EH 协作网络考虑上下行链路频谱共享、中继节点频谱共享、上下行速率匹配等的联合优化问题，通过对优化问题的数学解析，得到功率、带宽、功率分割等的数学解析表达式.提出可行的资源分配算法，并进行仿真验证.仿真结果表明，从系统能效与带宽分配系数、中继数量、上下行传输速率比值、平均信道增益的变化关系来看，本研究算法均都取得良好的性能，对于研究无线EH 协作网络的资源分配具有积极的意义.未来计划考虑窃听场景下的保密协作通信系统，基于物理层安全的资源分配算法进一步研究优化系统的安全能效.