RIS 辅助双功能雷达与隐蔽通信系统性能优化

胡浪涛，杨瑞，黄崇文，刘全金，吴磊，谭镇坤

(1.安庆师范大学 电子工程与智能制造学院，安徽 安庆 246133；2.浙江大学 信息与电子工程学院，浙江 杭州 310058)

双功能雷达通信(dual-functional radar and communication, DFRC)系统与智能超表面(reconfigurable intelligence surface, RIS)都是下一代无线通信网络的关键技术.DFRC 系统可以实现频谱资源共享与硬件平台共享，缓解频谱资源的限制，实现无线通信与雷达传感功能的双赢[1-2].RIS可以通过大量低成本元件巧妙地调节信号传播，实现可重构的无线通信环境，提高未来无线通信系统的频谱与能量利用效率.为了支持同步信息传输和目标检测，有学者开展了DFRC 波形设计研究：Liu 等[3]研究了多输入多输出(multipleinput multiple-output, MIMO)雷达探测，设计了多用户MIMO 通信的波束赋形；Ma 等[4]设计了DFRC 系统的隐蔽波束赋形.

RIS 的每个智能超表面单元的振幅和相位参数都可以调整，以便增强基站的输入信号，并实时反射给用户，从而经济有效地提高网络性能[5].RIS 处的无源波束赋形可由基站(base station,BS)通过RIS 控制.为了使RIS 的增益最大化，基站和RIS 的波束赋形通常是联合设计的[6].RIS 已在辅助雷达系统方面显示出优势[7].为了提高检测性能，Wu 等[8]分别对MIMO 雷达上用于目标检测的主动波束赋形和RIS 上的被动波束赋形进行优化，提出RIS 辅助检测算法，基于该算法的仿真结果表明RIS 可以产生更好的Cramér-Rao 界.上述研究用于RIS 建模的为单连接可重构阻抗网络，Buzzi 等[9]提出广义RIS 模型，其中RIS 网络是全连接，区别于传统的单连接RIS 网络模型[5-8].在DFRC 系统中，雷达和通信之间存在不可避免的折中[10]，这表明需要降低雷达性能以提高通信性能，反之亦然.在DFRC 传输方面，包含在探测波形中的关键信息很有可能会暴露给雷达目标，这些目标有可能成为对方的窃听者.因此，DFRC 系统的安全问题不容忽视.已有从物理层安全的角度开展的DFRC系统的保密性研究[11-12].Deligiannis等[11]考虑了带有恶意雷达接收机的统一通信和无源雷达系统，通过设计雷达波形和通信发射协方差矩阵，在不同的资源调度方案下，最大化雷达接收机的信噪比.Chalise 等[12]针对窃听雷达目标采用人工噪声辅助的安全传输方案，考虑到对目标位置和信道状态信息(channel state information,CSI)不确定性的不同假设，根据通信用户的信干噪比(signal to interference plus noise ratio, SINR)约束，将目标的信噪比降至最低.隐蔽通信与上述物理层安全技术[13]不同，隐蔽通信可以实现通信各方信息的隐蔽传输，防止通信信号被恶意窃听者发现[14-15].Ma 等[16]研究在隐蔽通信中部署RIS 的性能增益，通过联合设计Alice 处的发射功率和RIS 处的反射波束赋形矢量，最大化Bob 处接收信噪比.Zhou 等[17]研究窃听者Willie的位置对隐蔽通信速率的影响.该研究结果表明，当Willie 比合法用户Bob 离RIS 更近时，RIS 会提高隐蔽通信速率.上述有关隐蔽通信的研究中部署的RIS 均为单连接方式，未考虑全连接RIS 给隐蔽通信带来的影响.

本研究设计在双功能基站天线分离部署背景下的RIS 辅助多天线DFRC 隐蔽通信系统，联合设计双功能基站的主动波束赋形和RIS 相位偏转矩阵，最大化Bob 的隐蔽通信速率和目标处的探测功率.从Bob 隐蔽通信速率与目标处雷达探测功率增强方面，分析广义RIS 模型对DFRC 系统的影响，并与传统单连接RIS 模型进行比较.1)研究RIS 辅助的DFRC 隐蔽通信系统，针对双功能BS 天线的分离部署，提出多策略交替优化(multi strategy alternating optimization, MSAO) 算法，对通信波束赋形向量、雷达信号协方差矩阵和RIS 相位偏转矩阵进行联合设计，最大化Bob 的隐蔽通信速率和目标探测功率，使得通信和感知功能达到性能的折中.2)研究更为现实的场景，即Willie的非完美CSI 场景，通过利用所提MSAO 算法优化通信波束赋形向量、雷达信号协方差矩阵和RIS 相位偏转矩阵，来解决这一现实场景下的问题.在该场景下，隐蔽约束问题可通过S 引理与半定松弛(semidefinite relaxation, SDR)技术进行变换处理.3)从隐蔽通信速率、探测功率、波束方向图等方面与基准方案进行对比分析.仿真结果验证所提方案在实现通信质量和目标感知质量之间性能折中的有效性.

1 系统模型

1.1 信号模型

如图1 所示为RIS 辅助DFRC 的隐蔽通信系统, 该系统包含BS、无人机目标用户、合法接收器(Bob)与窃听者(Willie).Bob 接收来自BS 的直接信号和RIS 反射的信号.由于RIS 部署在远离目标的地方，目标在低空飞行，并且与BS 有很强的视距链路，因此通过RIS 反射的雷达回波信号相对较弱，可以忽略[18].在该模型中，假设BS 的M根天线以均匀线性阵列(uniform linear array,ULA)的形式部署.RIS 中部署N个反射元件.该系统在跟踪模式下作为雷达工作，以跟踪方位角为φm的目标.Bob 为单天线用户，假设Bob 可以忽略来自目标的反射信号[16].单天线Willie 在不断检测BS 与Bob 之间的通信信号，并试图识别BS 是否正在向Bob 发送信息.在BS 的分离部署中，有2 组天线：Mr根天线传输雷达信号、Mc根天线传输通信信号.雷达天线和通信天线的功率分别为Pr、Pc.假 设hb∈CN×1、hw∈CN×1分 别 为R I S 到Bob 和Willie 的信道，Hc∈CN×Mc、Hr∈CN×Mr分别为从通信天线和雷达天线到RIS 的信道.从通信天线和雷达天线到B o b 的直连信道分别为db,c∈CMc×1、db,r∈CMr×1，到Willie 的直连信道分别为dw,c∈CMc×1、dw,r∈CMr×1.假设所有信道遵循瑞利衰落，Bob 处的接收信号为

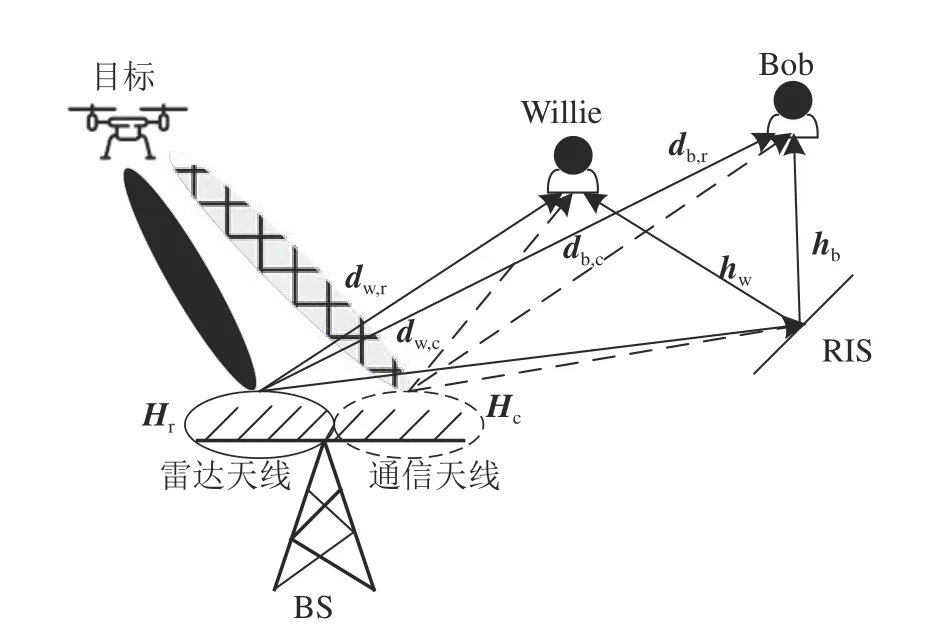
图1 RIS 辅助的DFRC 隐蔽通信系统模型Fig.1 RIS-assisted DFRC covert communication system model

式 中：G为 网 络 的 组 数，Θg∈CNG×NG为 全 矩 阵，NG=N/G为每一组网络的元件数.若G=1 ，则RIS为全连接网络；若G=N，则RIS 为单连接网络.Bob 的SINR、通信速率分别为

沿φm方 向 上 的 探 测 功 率 为

式中：a(φm)∈CM×1为 方向导向向量，对于ULA 部署，

其中 λ 为信号波长，d为天线间距，在不损失一般性的情况下，设置d=λ/2 ;C∈CM×M为整个发射信号的协方差矩阵，通信信号与雷达信号不相关，协方差矩阵可以表示为

式(6)改写为

式中：ar(φm)、ac(φm) 分别为雷达天线和通信天线的方向导向向量.

1.2 隐蔽通信

在本研究考虑的系统中，Willie 的目的是确定Bob 是否在与BS 进行通信.因此， Willie 的接收信号xw须进行2 种假设测试， H 0 为假设BS 仅发送雷达信号； H 1 为假设BS 同时发送雷达信号和通信信号.xw表达式为

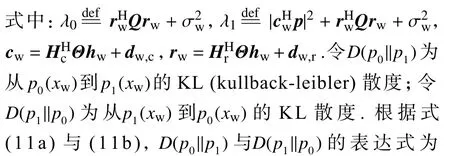
P{D1|H0}与P{D0|H1} 分别为 H 0 下的虚警概率和H1下的漏检概率.D 1 和 D 0 分别为对应于 H 0 和 H 1 的二元决策，即D1 为Willie 检测到Bob 正在通信，D0 为Willie 未检测到Bob 正在通信.检测错误概率是虚警概率与漏检概率的总和[20]:

式 中： 0 ≤ξ ≤1.0.若 ξ =0 ，则Willie 可以 完 美地 检测到BS 的信号传输.若 ξ =1.0 ，则Willie 无法执行正确的检测，Willie 希望最小化条件错误概率 ξ.似然比检验为

在D1 决策下，式(14)取大于等于1；在D0 的决策下，式(14)取小于等于1.

隐蔽通信中，窃听者Willie 试图找到使得总条件检测错误概率 ξ*最小的最佳检测器[21].对于任何给定的小常数 ε ∈[0,1.0]， ξ*满 足标准ξ*≥1-ε[20].因此，隐蔽约束为

下文将式(15a)表示为隐蔽约束 d1 ，式(15b)表示为隐蔽约束 d2.

1.3 优化问题建模

本研究旨在通过联合设计通信波束赋形向量、雷达信号协方差矩阵和RIS 相位偏转矩阵，在满足隐蔽约束、雷达恒模约束与总功率约束的条件下，最大化通信速率和雷达探测功率.将本系统的优化问题表示为

式中： ρ 为正则化参数，Q≥ 0 表示矩阵Q的所有特征值都大于或等于零，即Q为半正定矩阵.式(16)的第一部分为Bob的隐蔽通信速率，其余部分为沿φm方向上的探测功率；式(16a)为雷达施加的恒模约束，目的是保证最佳的低峰均功率比，减少雷达信号失真[22]；式(16b)为通信施加的总功率约束；式(16c)将雷达信号的协方差矩阵Q为赫米特半正定矩阵；式(16d)为RIS 的相位约束.

2 基于完美CSI 波束赋形设计

考虑以下典型的场景：Bob 处的信道状态信息完全已知，Willie 是非法用户.在此场景下，BS 可能会获得hw的完整CSI，使得Bob 在H1 下躲避Willie[23].此时，隐藏约束变为

根据上述隐蔽约束条件，优化问题式(16)可以重新表述为

注意，当隐蔽约束式(17a)与式(17b)同时满足时，可通过式(12a)与式(12b)推导出 λ0=λ1，从而得到cHwp=0 ，且在cHw的零空间中可以找到p的可行解.因此式(1 8 a) 可解.利用本研究提出的MSAO 算法，将问题式(18)分别转化为关于{p,Q}和 Θ 的2 个优化子问题，利用二次约束二次规划(quadratical constraint quadratic programming,QCQP)和SDR 技术来求解优化子问题.

2.1 优化通信波束赋形向量与雷达协方差矩阵

基于 Christensen 等[24]提出最小均方误差(minimum mean square error, MMSE)方法，将式(18)中的最大化Bob 隐蔽通信速率的问题转化为最小化均方误差的问题，过程如下.Bob 通过接收机gb接收到的信号为

均方误差为

MMSE 接 收 机gb,M为

在 Θ 已固定的情况下，式(18)可以转换成最小化均方误差和最大化探测功率的问题，即

由于式(22)中最后一项非凸，根据Xu 等[10]提出的变换方法，最后一项可以变换为

式(24)是QCQP 问题，先进行该问题的均匀化.将式(20)改写为

同理可以得到

利用SDR 技术[25]松弛T=pˆpˆH， 可以得到齐次QCQP优化问题：

2.2 优化相位偏转矩阵

固定p、Q，优化问题式(18)中涉及目标探测功率的部分可以省略：

对式(28)进行拉格朗日对偶变换[26]可以得到

式中： α 为拉格朗日乘子.固定 Θ 时，式(29)是关于α的无 约束 凸 优 化 问 题，最优 α*通 过 ∂f2/∂α=0 得到α*=γ.固定α时，式(29)可化简为分式规划问题.令θ=vecΘT，y∈C，应用Shen 等[27]提出的二次变换(quadratic transform, QT)，将问题式(29)变换为

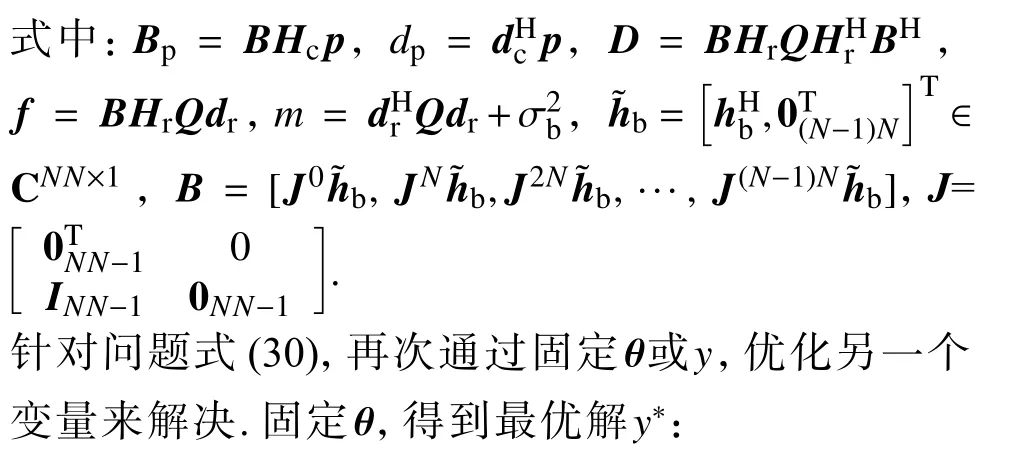
在固定y的条件下，问题式(30)简化为最小化问题：

在G=N(即RIS 为单连接)的特殊情况下，相位偏转矩阵 Θ 为对角矩阵，按照推导式(32)的相同路径，可以将 Θ 优化问题转换为凸的二次规划问题，利用CVX 工具箱求解.本研究提出多策略交替优化算法MSAO 来解决问题式(18)，算法流程如算法1 所示.

3 基于非完美CSI 波束赋形设计

一般来说，BS 很难获得Willie 的CSI，为此考虑更实际的应用场景如下：Willie 是窃听用户，不完美的信道状态信息cw被建模为[28]

式 中：cˆw为 估 计 的CSI， Δcw为 相 应 的CSI 误 差 矢量.Δcw以 椭 球 区 域 为 特 征，即

3.1 隐蔽约束d1

在隐蔽约束为D(p0||p1)≤2ε2的场景下，式(18)的优化问题可以改写为

问题式(35)是非凸问题，很难直接获得最优解，为此利用函数f(x)=lnx+x-1-1,x>0 的性质重新构造 隐 蔽 约 束，隐 蔽 约 束D(p0||p1)=ln(λ1/λ0)+λ0/λ1-1 ≤2ε2等价为

式 中：a、b为 方 程 l n(λ1/λ0)+λ0/λ1-1=2ε2的2 个根.式(36)重新表述为

将cw=cˆw+Δcw代入式(37)，利用SDR 技术松弛T=pˆpˆH，可以得到

式中： η1>0 ， η2>0.将问题式(35)近似为

式(40)为非凸优化问题，可以沿用完美WCSI 场景 下 的MASO 算 法 优 化 {p,Q} 、 Θ.当 固 定 Θ 时，将优化问题式(40)重新表述为

固定 {p,Q} ，将优化问题(40)重新表述为

Willie 非完美CSI 场景下MSAO 算法如算法2 所示.

3.2 隐蔽约束d2

在D(p1||p0)≤2ε2的场景下得到的优化问题与问题(33)除了隐蔽性约束条件不同，其他条件类似.同理，D(p1||p0)≤2ε2场景下的隐蔽约束条件D(p1||p0)=ln(λ0/λ1)+λ1/λ0-1 ≤2ε2等价为

其 中c与d是 方 程l n (λ0/λ1)+λ1/λ0-1=2ε2的2 个根.应用MSAO 方法来解决优化问题，这里省略详细的推导过程.虽然在这2 种场景中使用的方法相同，但在2 种不同的信号约束下，可实现的隐蔽率是完全不同的.

3.3 算法复杂度分析与收敛性分析

以算法1 为例，令问题式(16)的目标函数为f(p,Q,Θ)，这是最大化隐蔽通信速率和雷达探测功率的问题，在功率约束、雷达恒模约束和隐蔽约束约束条件下，f(p,Q,Θ)具 有上界.引入t作 为算法迭代次数，当固定{p，Q}时，根据式(28)与式(29)，有

且依据式(2a) 与式(2b) 对Θ 的约束，可以得到f1(Θ)收敛.

令问题式(22)的目标函数为f3(p,Q)，根据文献[25]对MMSE 算法收敛性的分析，可以判断出f3(p,Q)的第一部分是单调不增的，同时f3(p,Q) 其余部分也满足单调不增，即f3(pt+1,Qt+1)≥f3(pt,Qt).在功率约束、雷达恒模约束和隐蔽约束约束条件下，f3(p,Q)具 有下界，因此f3(p,Q) 整体收敛， 继而得到

即算法1 的收敛性分析成立.算法2 的收敛性分析与算法1 相同.

4 实验仿真分析

在本研究考虑的RIS 辅助DRFC 隐蔽通信系统中，资源平均分配给雷达和通信功能，即Mc=Mr=M/2和Pc=Pr=P/2， 系统功率为P=20 dBm.基站配备有M=16 的 天线ULA 阵列，RIS 配备有N=20 反 射 元件.在不失一般性的情况下，假设仿真模拟的相关具体参数如表1 所示.如图2 所示为在Willie 完美CSI 场景下和非完美CSI 场景下，Bob 的隐蔽通信速率R与算法迭代回合数S的关系.该图表明所提算法的收敛性.可以看出，适当改变 ρ 的大小可以提高Bob 的隐蔽通信速率，且所提算法可以在15 次迭代中达到收敛状态，表明所提算法复杂度较低.对比2 个场景可以明显看出，当 ρ 相同时，相较于Willie 非完美CSI 场景，完美CSI 场景下可以得到更大的Bob 隐蔽通信速率.

表1 RIS 辅助DFRC 隐蔽通信系统仿真参数设置Tab.1 Simulation parameters setting of RIS assisted DFRC covert communication system

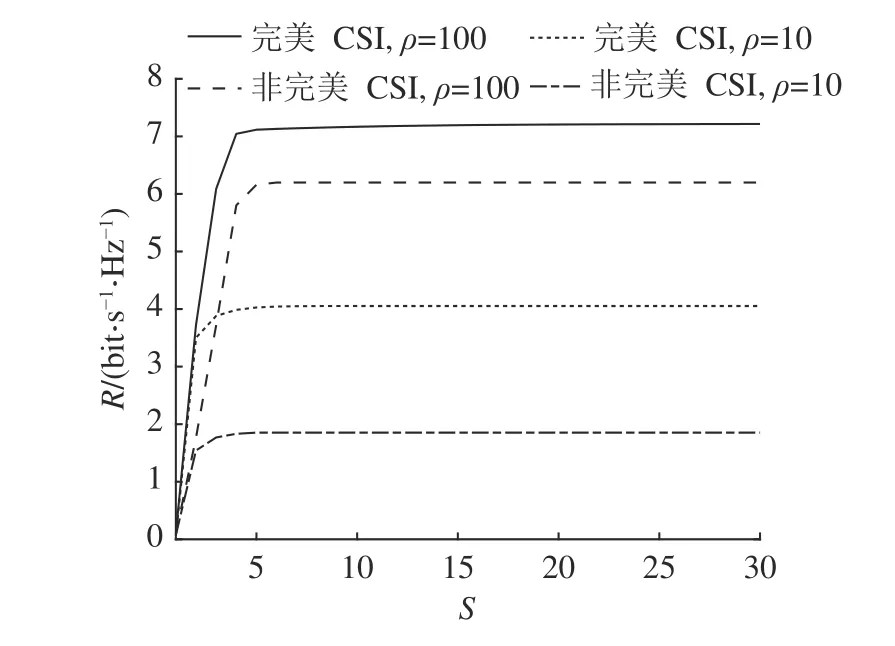
图2 多策略交替优化算法的收敛性Fig.2 Convergence of multi strategy alternating optimization algorithm

图3 为当Bob 隐蔽通信速率为7.6 bit/s/Hz 时，2 种Willie 场景下的波束方向图(beam pattern, BP).图中，PZ为功率增益，φm为角度.选择无RIS 辅助的通信感知一体化隐蔽通信系统[4]作为对比的基准方案.图3(b)中，全连接RIS 辅助相较于基准方案，可对波束方向图功率增益提高1.3 dBm，与单连接DFRC 隐蔽通信系统相比，波束方向图主瓣功率增益提高0.97 dBm.由图可以看出，有RIS 辅助的波束方向图优于无RIS 辅助的波束方向图，有RIS 辅助对旁瓣具有更大的抑制，且在全连接RIS 辅助下实现了目标处的最大探测功率.在Willie完美CSI 场景下，全连接RIS 辅助的系统探测功率比无RIS 辅助下的探测功率提高5.81%.对仅有雷达感知功能的波束方向图进行仿真，结果表明全连接RIS 辅助的波束方向图的主瓣更加接近仅雷达感知时的性能.

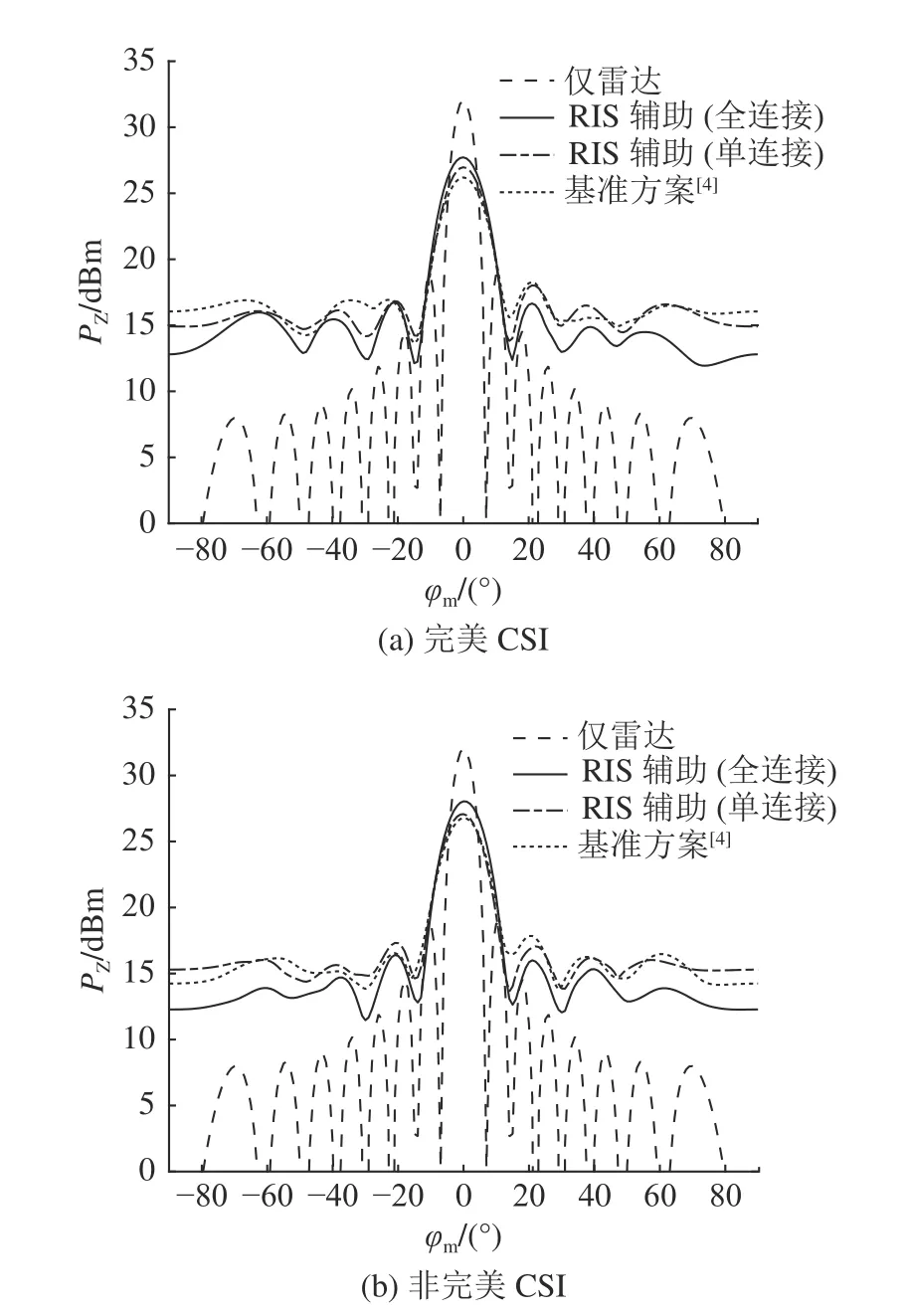
图3 2 种Willie 场景下的波束方向图比较Fig.3 Comparison of beam pattern in two Willie’s scenarios

由于问题式(16)是多目标优化问题，可以通过改变正则化参数 ρ 来获得帕累托最优前沿，这能够揭示不同目标之间的权衡关系，即目标探测功率 β 和Bob 的隐蔽通信速率.如图4 所示为RIS辅助和正常DFRC 系统的帕累托最优前沿.由图可以观察到通信与感知性能的折中现象，即必须降低探测功率以提高Bob 隐蔽通信速率，反之亦然.同样明显的是，与没有RIS 辅助的DFRC 系统相比，有RIS 辅助的情况下，系统的整体性能更具有优势.图中无RIS 辅助可实现速率区域完全包含在有RIS 辅助的可实现的速率区域中，相对无RIS 和单连接模式，广义全连接RIS 辅助的折中曲线向右上角扩张，这表明广义全连接RIS 部署可以提高隐蔽通信系统通信和感知的自由度.还可以观测到，在非完美CSI 场景下，无RIS 辅助时，Bob 隐蔽通信速率明显低于完美CSI 场景下的速率，但在部署RIS 后，Bob 隐蔽通信速率仅略低于完美CSI 场景下的速率，这表明RIS 辅助通信系统具有帮助提高通信速率的优点.在Willie非完美CSI 场景下，Bob 的隐蔽通信速率在单连接RIS 辅助下较无RIS 辅助提高了3.99%.虽然RIS 实现了Bob 隐蔽通信速率的较高上限，但探测功率的上限保持不变，原因是探测功率完全由BS 决定，有无RIS 基本上没有区别.

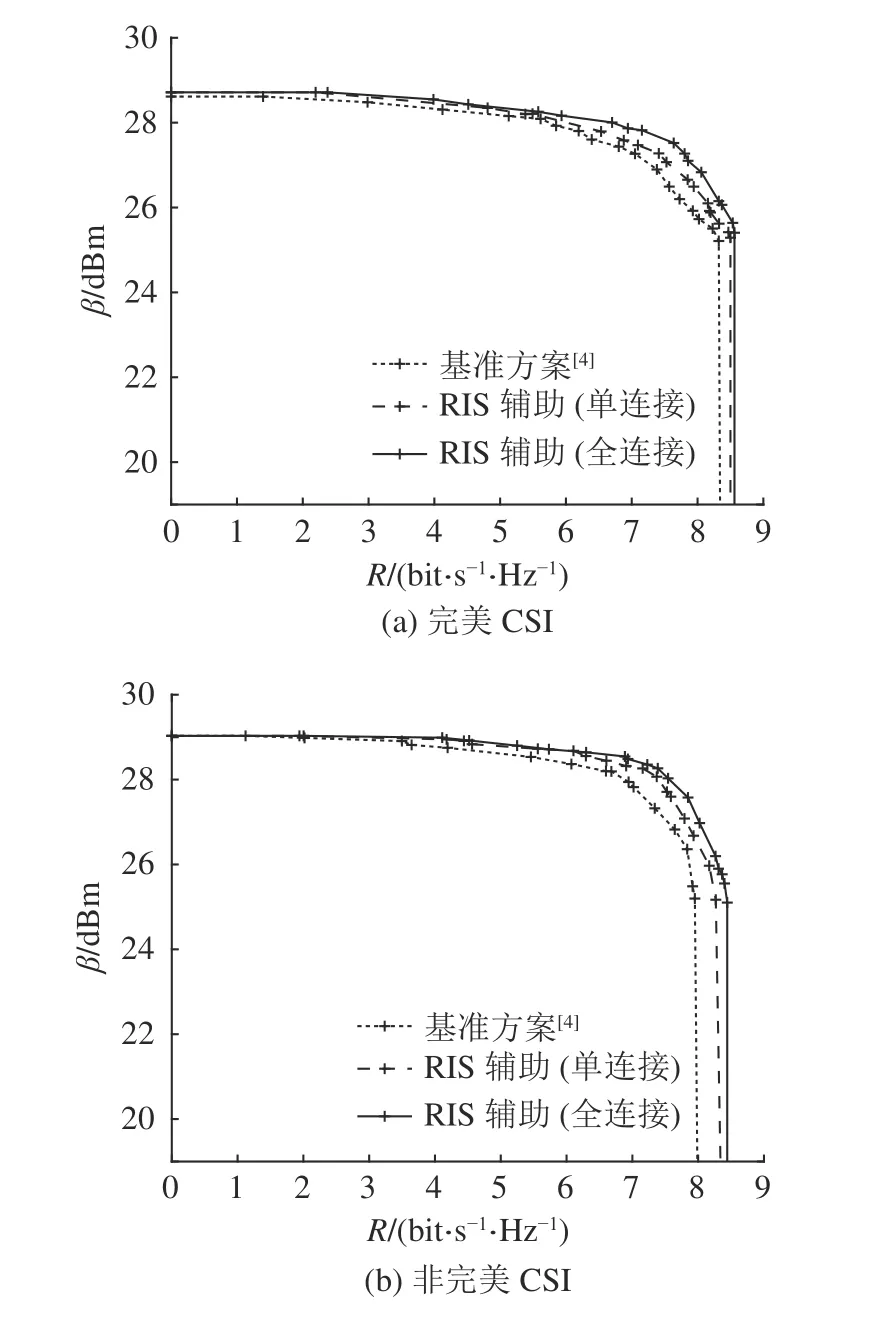
图4 2 种Willie 场景下目标处的探测功率与Bob 隐蔽通信速率的折中Fig.4 Tradeoff between probing power at target and Bob’s covert rate in two Willie’s scenarios

如图5 所示为RIS 反射元件数量对目标处探测功率的影响.由于全连接和单连接RIS 在视距信道中的性能相同，图中只考虑单连接RIS.可以看到，随着RIS 元件数量的增加，在目标处可以实现更好的波束方向图和更高的探测功率，提升系统性能，但这种改进不是无限增长的，而是渐近地达到上限的.如图6 所示为在不同水平位置部署RIS 对波束方向图的影响.仿真可以看到，RIS 的最佳水平位置靠近Bob 位置，RIS 部署在(200, 0) m的位置，实现了最优波束方向图.同时，在RIS 从靠近BS 的位置向Bob 位置移动的过程中，波束方向图体现出逐渐提升的效果.在超过最佳水平位置后，波束方向图是在逐渐衰减，系统性能降低.

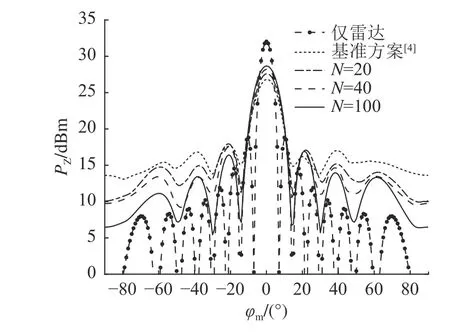
图5 RIS 反射元件数量对波束方向图的影响Fig.5 Effect of number of reflective elements of RIS on beam pattern

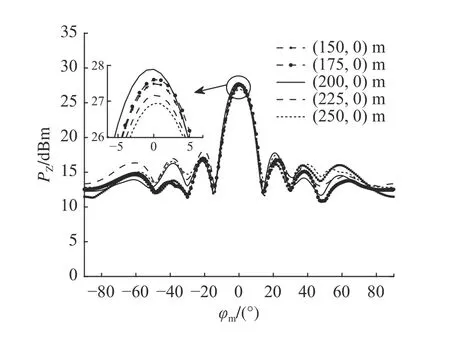
图6 RIS 水平部署位置对波束方向图的影响Fig.6 Effect of RIS horizontal deployment location on beam patterns

如图7 所示为在CSI 误差vw=0.001 的条件下， ε 与Bob 隐蔽 通信速率的关 系.由于 只考虑了单连接RIS，图中展示的模拟结果与理论分析一致，即当 ε 增大时，隐蔽性约束变得松散，导致Bob 的隐蔽通信速率增大.还可以观测到，在隐蔽约束 d1 条件下的Bob 隐蔽通信速率略高于隐蔽约束 d2 条件下的值.如图8 所示为当C S I 误差vw=0.001时，2 种KL 散度情况下的检测误差概率与 ε 的 关 系.图 中，P1-d1 表 示 在D(p0||p1)≤2ε2条 件下的虚警概率，P2-d1 表示在D(p0||p1)≤2ε2条件下的漏检概率，其中P1为虚警概率P{D1|H0}，P2为漏检概率P{D0|H1}，其他符号被类似地定义.仿真发现，在2 种隐蔽约束的条件下，P1与P2均随着ε的增加而减小，且虚警概率总是低于漏检概率.检测误差概率随 ε 的增加而减小这一现象表明，隐蔽性约束越宽松，Willie 的检测性能越好.此外，虽 在 ε =0.01 时，无RIS 辅 助 的 场 景 中 虚 警 和漏检概率略高于有RIS 辅助下的概率值，但随着ε的增大，有RIS 辅助场景中的虚警和漏检概率均高于无RIS 辅助下的概率值，验证了本研究提出的波束赋形器设计在隐蔽通信中的有效性.

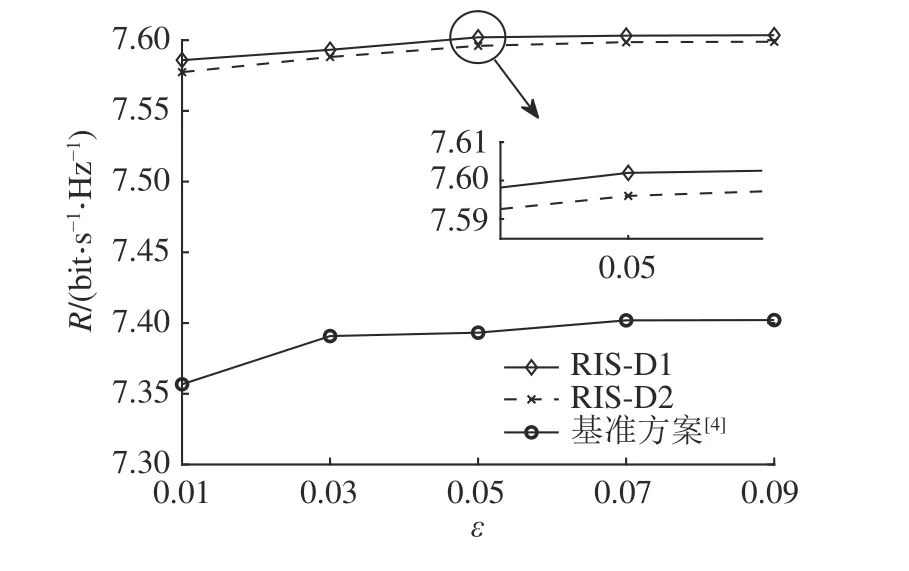
图7 隐蔽性阈值与Bob 隐蔽通信速率的关系Fig.7 Relationship between covertness threshold and Bob’s covert rate

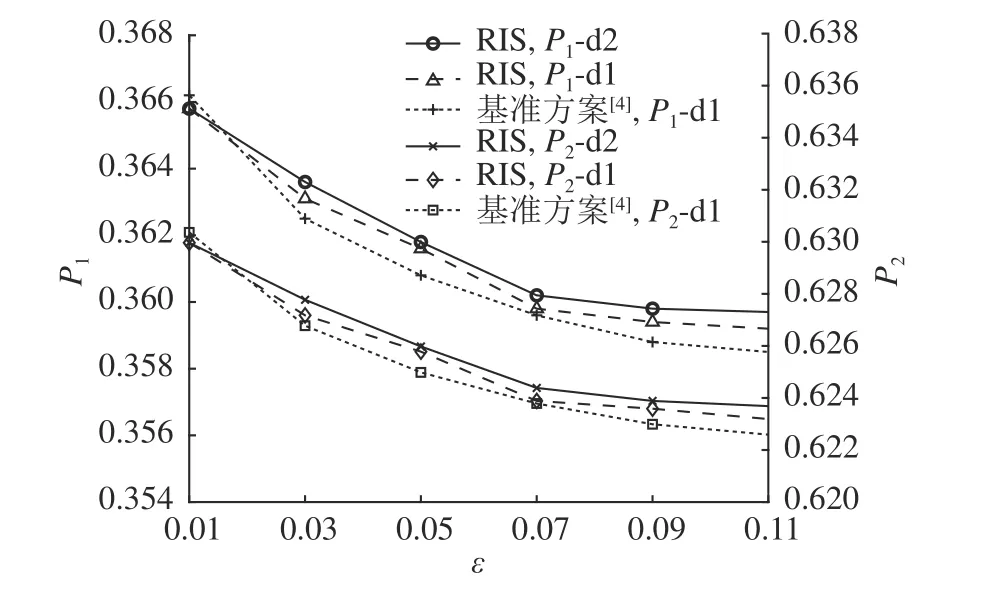
图8 隐蔽性阈值与检测错误概率的关系Fig.8 Relationship between covertness threshold and probability of detection error

5 结 语

本研究通过部署RIS 来提高DFRC 隐蔽通信系统的性能.针对RIS 辅助DRFC 隐蔽通信系统，提出MASO 优化算法，联合设计通信波束赋形矩阵、雷达信号协方差矩阵和RIS 相位偏转矩阵，在满足隐蔽约束、雷达恒模约束和总功率约束的条件下，最大化Bob 的隐蔽通信速率和目标处的雷达探测功率.所提MSAO 算法旨在解决BS 天线分离部署中的主动与被动波束赋形的非凸优化问题.采用广义全连接RIS 模型，并与广泛使用的传统单连接RIS 模型进行比较.实验仿真结果证实了所提方案的可行性与有效性.本研究的RIS 辅助DFRC 隐蔽通信系统基于BS 天线分离部署，并未考虑BS 天线共享部署的场景，因此所提方法是否适用于共享部署的场景有待结合RIS 辅助定位的性能进行进一步研究.