空间几何体外接球问题的四种常见类型

蔡志山

(福建省莆田市妈祖中学)

空间几何体的外接球问题作为高中数学立体几何模块中的一类重点问题,是高考中的热点.求解空间几何体外接球问题的关键是正确寻找外接球的球心或确定外接球的半径.空间几何体的形式多样,题目类型变化多端,给寻找外接球的球心或确定外接球的半径等造成很大的困难.本文结合空间几何体的不同结构特征加以合理归类,总结空间几何体外接球问题的四种基本模型.

1 墙角模型

墙角模型是指三棱锥的三条棱两两垂直或三个平面两两垂直,将该三棱锥放入长方体中,把该三棱锥的外接球转化为该长方体的外接球,不用找出球心的具体位置,即可求出该球的半径.图1给出三种不同情况的三棱锥P-ABC的墙角模型.

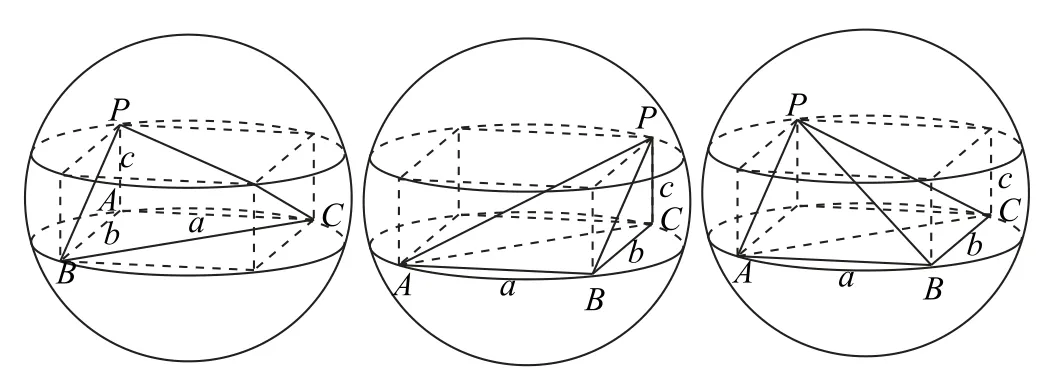
图1

例1 在三棱锥P-ABC中,已知PA,PB,PC两两垂直,且PA＝1,PB＝2,PC＝3,则三棱 锥P-ABC的外接球的表面积为( ).

A.13π B.14π C.56π D.64π_____

把三棱锥P-ABC放置在一个长方体中,如图2所示,则该长方体的外接球即为三棱锥P-ABC的外接球,其外接球的半径为

图2

所以三棱锥P-ABC外接球的表面积为S＝4πR2＝14π,故选B.

求解此类墙角模型问题的关键:一是“见数思形”,需在草稿纸上画出三棱锥的草图,判断是否有两两垂直的三条棱;二是“会构图形”,即灵活构造长方体;三是“会用公式”,4R2＝a2＋b2＋c2(其中R为该三棱锥的外接球的半径,a,b,c为两两垂直的三条棱的长).

2 对棱相等模型

对棱相等模型是指三棱锥的相对的两条棱相等,可以通过构建长方体,将该三棱锥放入该长方体中,使三棱锥的顶点与长方体的顶点重合,进而将该三棱锥的外接球转化为该长方体的外接球,从而求出该外接球的半径.图3 是四面体ABCD的对棱相等的模型.

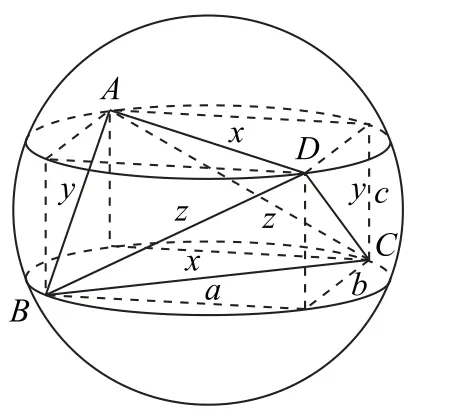
图3

图4

例2 在平行四边形ABCD中,AB＝2 2,BC＝3,且,沿BD将△BDC折起,使点C到达点E处,且满足AE＝AD,则三棱锥E-ABD的外接球的表面积为_________.

E-ABD的外接球相同,所以三棱锥E-ABD的外接球的表面积为S＝4πR2＝13π.

求解此类对棱相等模型问题的关键:一是通过翻折,明确不变与变化的量;二是构造,即根据所给的相等对棱的长度,构造符合条件的长方体;三是列出方程组,即设出长方体的长、宽、高,根据三棱锥的三组对棱的长度,列出方程组,解方程组即可求出所构造的长方体的共顶点的相邻的三条棱的长;四是用公式,利用长方体的体对角线长等于该三棱锥的外接球的直径,求出该三棱锥的外接球半径,最后利用球的表面积与体积公式即可得到外接球的表面积与体积.

3 “心有所依”模型

“心有所依”模型是指对于圆锥、圆台及侧棱相等的棱锥等几何体,可得球心必在该几何体的高所在的直线上,或者在棱锥一个底面的高所在直线上,由此可把相关信息集中到某一个直角三角形内,利用勾股定理求解.图5 是三棱锥P-ABC的“心有所依”模型.

图5

例3 已知三棱锥M-ABC的四个顶点均在表面积为32π 的球面上,,AC＝4,则三棱锥M-ABC的体积的最大值为( ).

根据题意可知△ABC是一个直角三角形,其面积为4,其外接圆的圆心在斜边AC的中点上.设外接圆的圆心为Q,当MQ⊥平面ABC时,三棱锥M-ABC的体积最大(如图6),设球心为O,半径为R,则有4πR2＝32π,解得R＝2 2,而点O到平面ABC的距离为,所以三棱锥M-ABC的体积的最大值为,故选C.

图6

求解此类“心有所依”模型问题的关键:一是确定球心O的位置,先确定底面三角形的外接圆的圆心;二是计算出三棱锥底面外接圆的半径;三是利用勾股定理,即可求出球心到底面的距离,从而求出三棱锥的高.

4 “双心”模型

“双心”模型是指可利用球心、三角形(或四边形等)外接圆的圆心,以及外接圆与球的交点所构成的直角三角形进行求解.图7是三棱锥P-ABC的“双心”模型.

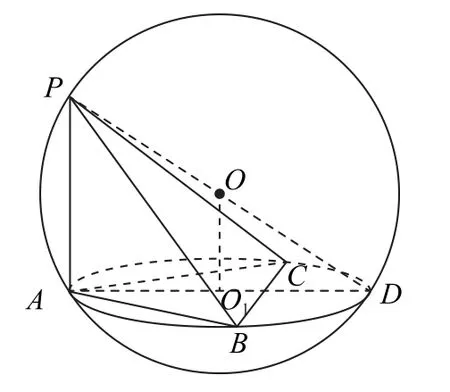
图7

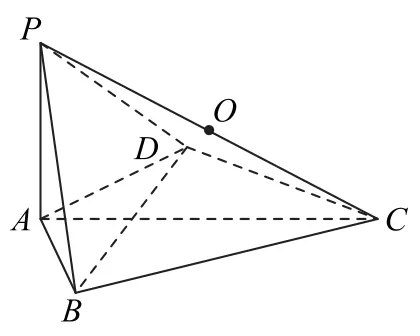
图8

例4 在四棱锥P-ABCD中,PA⊥底 面ABCD,PA＝AB＝AD＝1,BC＝CD＝BD＝3,则该四棱锥的外接球的表面积为__________.

求解此类“双心”模型问题时,外接球球心到各顶点的距离相等,因此可以先考虑到三个顶点的距离相等的点是三角形的外心,球心一定在过此点与此平面垂直的直线上.