一道高中数学小题的算法分析

马建

【摘  要】  本文通过一道数值估算小题，用常用算法、改进算法、巨难算法、最优算法来进行分析比较，对于估值计算，大多情况下学生解题时都要使用到题目中所给出的参考数据.如果出现其他的数据，再寻找关系进行等价转换.类似的问题选择合适的算法，提高运算的速度和解题的正确率，在高考中从容面对各种运算问题，才能顺利解答相关问题，完美体现出数学算法表征．本文又举例一道高考题，学生当年高考的时候也算不出来，分析主要原因在于没有认真审题，所以，数学运算前提都要进行阅读和认真审题.

【关键词】  高中数学；数据估算；数学算法表征

高中学生只有具备良好的运算能力，才能顺利解答相关问题．高考对学生的运算能力提出了较高的要求，运算能力也反映了学生的学习水平．高中学生正处于能力培养的关键阶段，数学教师必须重视其运算能力的培养．因此，在教学的过程中，教师要根据学生的学情和心理状态，应用创新性教学策略，全面提升学生的运算能力．

数学算法表征，是数学其他表征中最突出的一个表征，它与数学的其他表征都有交集和融汇，在各种问题的解决中，必不可少.

下面，通过一道最近的高三数学小测试中数值估算小题来进行研究和分析数学的多元表征中，算法表征的应用.

1  例题

（2022年12月广东省中山市中山纪念中学高三周测训练）已知某种装水的瓶内芯近似为底面半径是4dm、高是8dm的圆锥，当瓶内装满水并喝完一半，且瓶正立放置时（如下图1所示），水的高度约为（   ）（本题使用的参考数据， ）

（A） 1.62dm.       （B） 1.64dm.

（C） 1.65dm.       （D） 1.66dm.

2  数学表征分析

上题中的数学文字表征表述得十分清晰，数学图形表征也是简单明了，并且学生在解答本题的时候对“瓶内装满水并喝完一半”这句话的理解是没有任何问题的，它的准确表示是体积的一半，而不是表示喝了水高度的一半，从题目的问题也能看出来，本题主要是求这个几何体进行体积.

本题的考查目标：数学的文字表征、数学的表征图形、数学的公式表征、数学的运算表征、数学的算法表征等多元表征，同时也考查了学生的审题能力.

3  用常规算法求得准确值但不是正确答案，改进算法后进行原因分析

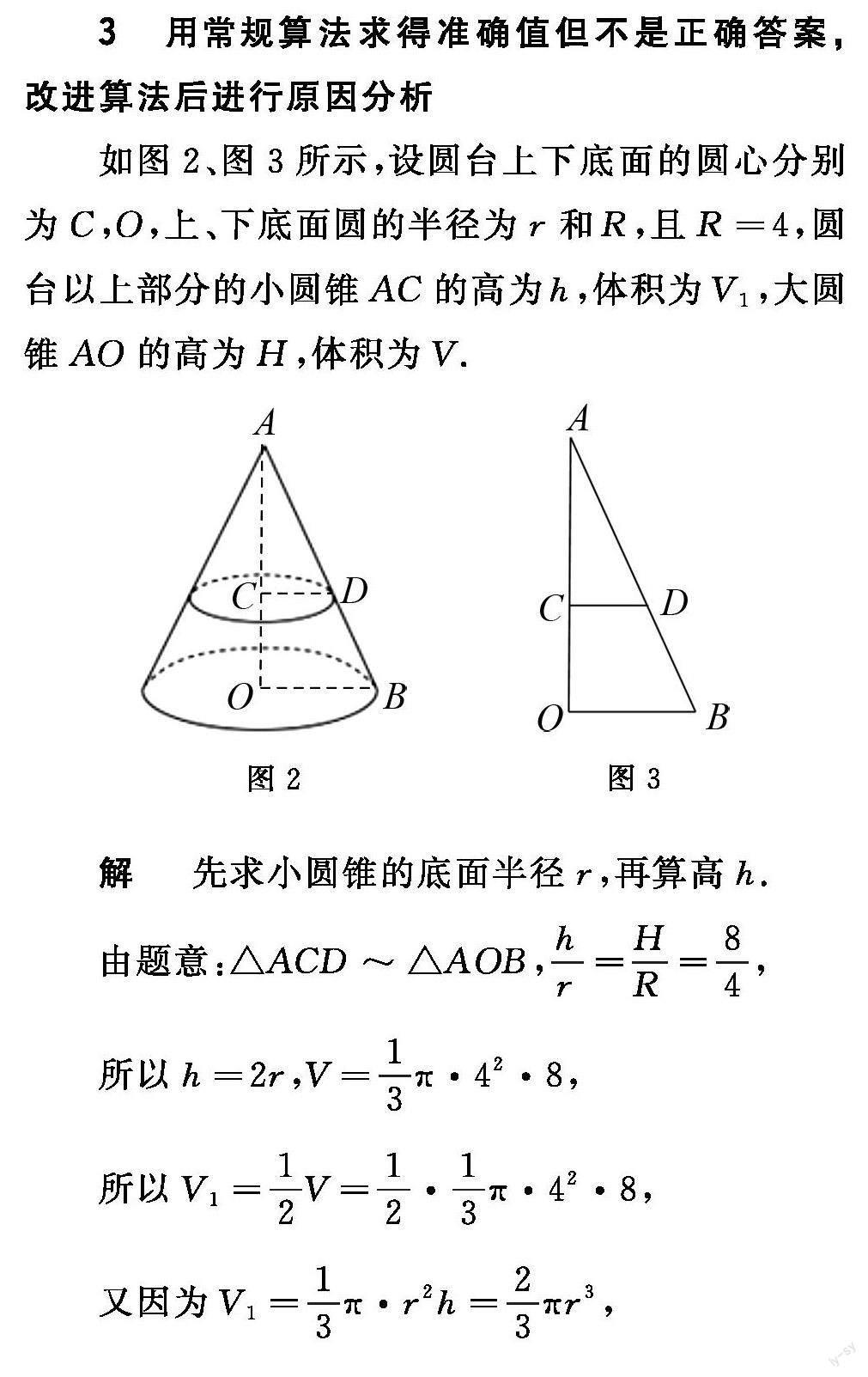
如圖2、图3，设圆台上下底面的圆心分别为，上、下底面圆的半径为和，且，圆台以上部分的小圆锥的高为，体积为，大圆锥的高为，体积为.

解  先求小圆锥的底面半径，再算高.

由题意：，，

所以，，

所以，

，

所以，

得，

所以，

所以，

所以水的高度为，

其实这就是本题问题的准确值，但题目显然是要求利用所给的数据来求水的高度的近似值，而题目中并没有给出的近似值，所以，需要将进行进一步的处理.有同学还发现有这个关系可以用，但是这个数不能够直接完全开出来，接下来就用两种常用的算法对这道题进行计算.

3.1  常用算法1

用手动平方的方法，来估算的近似值.

经过一些手动平方计算发现：，，所以可以取近似值1.26，甚至小数点再向后取一位，这样可以算到已经非常接近了，所以可取的近似值为1.261.

代入最后的式子，求得了水的高度为：，选（D）（错误答案）.

3.2  常用算法2

假如有记忆力非常好的同学，或者是刻意记住了一些特殊根号的近似值，记住了的准确近似值为，直接把代入了最后的式子，最后求得了水的高度为：，选（C）（错误答案）.

以上这两种算法都求出了水的高度的近似值，而且是较准确的值，但并非正确答案，那么问题到底出在哪里，学生到底该怎么计算这道题呢？

3.3  改进算法3

将先求上底面圆的半径，直接改为求小圆锥的高.

把前面得到的结果稍加改变后：，所以，从而得到了，这样小圆锥的高为，这样就出现了题目给出的参考数据：，把这个近似数代入题中，求到了小圆锥的高.

下一步代入最后的式子，求得水的高度为：，得到了正确答案，选（B）.

3.4  学生计算错误的原因分析

虽然由算法1、算法2得到了较准确值，这些值却不是题目的正确答案，分析具体原因有以下两点.

错误原因1  前面两种算法，算法1、算法2算错答案的原因，都是先算小圆锥的底面半径，再算小圆锥的高.小圆锥的底面半径在计算过程中已经开始进行近似取值了，这就能产生由近似值带来的下一步计算产生误差，计算小圆锥的高，让误差加倍，再经过了一次除法运算，然后再取近似值，最后算出的结果，这样的多步骤运算，它的算法和计算数据都能共同产生的误差，这样产生的计算误差我们很难控制.所以，做这样的估值题目，一定要用到题目给出的数据.还有同学根本没有用题目所给的数据，直接得到结果，也属于审题不到位导致错误.

错误原因2  原本题目给出的近似数据就有误差：题目给出的是，但是的更精确的数据可以为，用这两个不同的近似数值计算产生了误差，和之间产生的的偏差，乘以了4之后的结果对小数点后的第二位数有影响.但是，这道近似估值计算题，给的数据保留到小数点后两位也确实是没有问题的，这样算来就产生的误差.

3.4  典型的巨难算法4

直接求圆台的上底面半径或者高，

设圆台的体积为，

则，

整理得：.

这个算法看似非常简单、直接，但得到上面的三次方程后就很难把它解出来了.又或者把求上底面半径转换成求小圆锥的来试一下，

有：.

整理得：，这个三次方程同样很难解出来.

3.5  最优算法5

利用相似几何体的相似比来做这道题.其实，这道题可以直接使用相似几何体的体积比为等于它们对应边比的立方来求解.

由大小圆锥相似，易得：，.

接下来就遇到了和前面同样的困境：无法正确表达出来.

其实，学生除了能找到了和有平方关系外，还可以发现：，然后把结果右边的分数的分子和分母同时乘以来进行这样的处理，

处理之后就得到了：，这样，就可以把成功地转换成来进行近似计算了，代入求得结果：.

从而代入最后的式子，求得水的高度为：，得到正确答案，选（B），题目得到完美解决.

4  分析问题

综上几种不同的计算方法，表面上看都能解决本题的问题，但是，作为近似计算的题目，大多要用到，也是必须用到题目中给出的参考数据，对于计算结果中没有出现的新的数据，学生要想办法寻找数据之间的关系或者变形来进行解决，进行等价转换.不同的算法过程不一样，结果一样，但是得到结果所花费的时间也不一样，学生可以对这些算法进行对比和总结，从而可以找到快速有效解决这些问题的最优算法.

数学高考考试大纲中对数学运算能力的要求实质就是“多思少算”．所以通过研究高考试题的特点，多了解、理解算理，改进计算的方法，减少在高考解题过程的计算量是赢得考试时间和考试成功的重要途径[5].

数学多元表征的类型系统，在科学研究中一般使用语言描述、数值表示和图像显示三种表征形式[2].数学的数值表示在各种问题考核中都是最直观、最清晰的有效表述.在高考中，每道数学题都把数学多元表征的融合表现得淋漓尽致.近年来，为了体现教育公平，有很多省份都陆续加入了全国统一考试的行列，同时，近几年的数学高考题，对数学运算能力的要求也是越来越高，考查的内容和方向也是多种多样，如果没有好的数学运算思想和数学运算方法，在高考答题中一定会大大减慢答题速度，甚至影響到整张试卷答题的完整性，有的甚至出现算了半天，得到了错误的结果，所以，教学过程中要加强对数学算法的分析和总结.

本题不能得到正确答案的原因还有就是，没有经过认真审题，这种错误的原因就是拿到了题目就开始闷头计算，没有看到题目后的小括号里的补充说明，根本没有看到（本题使用的参考数据，），或者学生认为不需要这个他可以直接求出来.事实上，他确实可以求出结果，只不过求到的不是正确答案而已，这种情况完成以自我的中心，根本不管题目.因此，学生在今后的读题、审题过的程中，一定要把题目看完整，也包括把题目中所给的附加括号的条件，或者试卷题头中出现的公式、数字记住，甚至练一个标点符号也不要放过.在高考过程中，学生拿到试卷后打铃前的五分钟，切记不要急于做前面的几道小题，拿到高考试卷后应该先把整张试卷通览一遍，包括试卷前给的文字和公式等，做到心中有数，简单判断了各个题目的大致难易程度，打铃之后再认真地从第一题开始作答.

5  变式练习

本文最后再给大家创造一个训练的机会，不妨将第一个例题进行一个小的改编：若将水瓶倒置喝完水瓶一半高度的水后，再将水瓶进行正立旋置如图1，问：此时水瓶中的水的高度是多少？（参考数据）（参考答案：水瓶中的水的高度约为）

6  结语

在高中数学的解题过程中，审题尤为重要，这是能正确算出结果的一个充要条件.审题关键之一在于要逐字逐句看，看清楚问题.特别是要注意容易看错和被忽略的字词.审题关键之二在于要学会转化问题.对一些题目，题目背景很长，给出的已知条件和结论都很繁杂，在审题时，可将条件和问题重新整理在草稿纸上，并进行简化，学会化繁为简.审题关键之三还在于要注意题目中的隐含条件.有一些题目的题干中给出的条件并不是那么明显，需要对一些隐含的条件要进行深入地思考、分析、挖掘和加工之后才能运用到解题过程中.此外，在审题过程中还可以通过画出相应的图形等直观地进行问题分析.

【基金：广东省教育科学规划2022年度中小学教师教育科研能力提升计划项目一般课题“基于数学表征的高中生运算素养培养实践研究”（课题编号：2022YQJK554）阶段性研究成果之一】

参考文献：

[1]普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社出版，2020.05.

[2]唐剑岚.数学多元表征学习的认知模型及教学研究[M].南京：南京师范大学出版社，2009.07.

[3]姚建法.数学多元表征研究综述[J].江苏教育研究，2020（13）：53-59.

[4]王佳荣.高中学生数学运算能力的培养策略[J].数学学习与研究，2022（26）：116-118.

[5]张展彬、王位高.优化高考运算能力的策略[J].中学数学研究，2010（09）：7-10.

[6]张梅.数学解题的本质——审题[J].课程教材教学研究（中教研究），2022（07）：34-35.