圆中图形繁琐多 化繁为简是条路

刘 琦

(昆明理工大学附属中学,云南 昆明 650031)

中考中对圆的考查大多都是以圆与直线形(线段、射线、直线、三角形、四边形、多边形称为直线形)图形组合成复杂图形为背景,以运动为载体,集代数与几何知识于一体,渗透分类讨论、转化化归、数形结合、函数与方程等数学思想.常涉及垂径定理、弦、弧,圆心角的关系、圆周角定理、切线性质与判定、切线长定理、勾股定理,相似三角形的判定和性质,特殊四边形性质以及锐角三角函数定义与特殊角的三角函数值等相关知识.

下面结合中考真题,谈谈如何在圆的计算题与证明题中分析条件、化繁为简、快速解题.

1 连半径,证垂直

例1(2020年铜仁市中考题)如图1,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.

(1)求证:CD是⊙O的切线;

图1 例1题图 图2 分析附图

分析(1)如图2,此问属于“连半径,证垂直”,即连接OC,利用题设中的直角或垂直条件推导出半径与直线垂直,得出∠OCD=90°即可,抓住△CBE与△ABC这对“共边相似三角形”是关键.

(2)如图2,设BC=k,AC=2k,抓住△DCB与△DAC这对“共边相似三角形”,根据相似三角形的性质即可得到结论.

解(1)如图2,连接OC.∵AB是⊙O的直径,∴∠ACB=90°.

∵CE⊥AB,∴∠CEB=90°,

又∠ECB+∠ABC=∠ABC+∠A=90°,∴∠A=∠ECB.

∵∠BCE=∠BCD,∴∠A=∠BCD.

∵OC=OA,∴∠A=∠ACO,∴∠ACO=∠BCD,

∴∠ACO+∠BCO=∠BCO+∠BCD=90°,

∴∠DCO=90°,∴CD是⊙O的切线.

(2)∵∠A=∠BCE,

设BC=k,则AC=2k.

∵∠D=∠D,∠A=∠BCD,∴△ACD～△CBD,

2 阴影部分面积

例2 (2020年黔西南州中考题)如图3,在△ABC中,CA=CB,∠ACB=90°,AB=2,D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为____.

分析将下方的阴影部分旋转到最上方,转化为计算规则图形弓形的面积.

图3 例2题图 图4 旋转、割补

解法2 如图4,∵∠EDF=∠CDB=90°,∴∠EDC=∠FDB=90°-∠CDF,

∴扇形EDC与扇形FDB面积相等.

∵DN=DM,DB=DC,∴△DCM≅△DBN,

∴阴影部分EMC与阴影部分FNB面积相等,

∴所求阴影部分面积为弓形CFB面积.

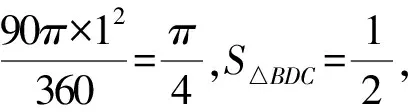
点评求阴影部分面积常有以下方法:①公式法:如果阴影部分是扇形、平行四边形、圆等,直接用公式计算;②和差法:将不规则阴影部分转化为规则图形求面积的和差,有时需要作辅助线进行分割;③等积转化法:将图形平移、轴对称、旋转等转化为公式法或和差法,注意利用平行线中的等底(同底)等高(同高)转化;④容斥原理法:阴影部分是两个基本图形互相重叠得到的,“组合图形面积”=“两个基本图形面积之和”-“重叠图形面积”.

3 线圆相切求半径

图5 例3题图

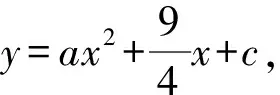
图6 作平行线

综上,抛物线上不存在点Q,使得△QCO为等边三角形.

如图7,当⊙M与x轴相切时,

图7 M在P的上方 图8 M在点P的下方

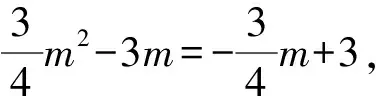
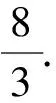
图9 M在点P的下方 图10 M在点P的上方

对于圆这类综合性较强的题目,多采用由因索果以及执果索因相结合的方法进行分析,以便达到条件与结论的有效沟通.同时又要善于挖掘题目中的隐含条件,将问题转化到基本图形之中,再用相关的知识与方法进行解决,这样可以达到化繁为简、快速解题的效果.