一道平行线中角度问题的教学实录

莫益群

(浙江省宁波市余姚市三七市镇初级中学,浙江 宁波 315412)

对平行线问题的处理和简单角度问题的计算,是初中生必备的能力.学生在解决这类试题的过程中,可以提高计算能力,培养直观想象素养.

1 试题呈现

笔者在课堂上呈现如下试题:

如图1所示,已知l∥m,∠1=135°,∠2=95°,求∠3.

图1 试题图

2 百花齐放,解法荟萃

经过2分钟的思考后,生1给出了如下解答.

生1:解法1 如图2所示,作直线n∥l.

教师点评生1的解法思路清晰、过程简洁,很精彩,充分利用了平行线的性质,两条平行线被第三条直线所截,这是平面几何中一个重要的解题模型[1].

图2 解法1图

生2观察生1的解答过程,受到启示,给出了如下的解法.

生2:解法2 延长AB,JC交于点H,如图3所示.

∵m∥l,∴∠1+∠BHC=180°.

∵∠2=∠BHC+∠BCH=∠BHC+180°-∠3,

∴∠1+∠2+∠3=∠BHC+180°-∠3+∠1+∠3=∠BHC+∠1+180°=180°+180°=360°,

∴∠3=360°-135°-95°=130°.

教师点评与解法1相比,解法2也是通过构造平行线被第三条直线所截来做的,构造辅助线后图形不如解法1的对称,相应的解题过程也就更繁琐了.不过能有如此的探究精神,是值得表扬的.

如果应用对称的思想,则图1中AB、BC是平等的,延长AB,JC可以解决,那么延长CB、KA交于一点也必定可以解决,而且过程完全相似.同学们下课后自己去试试.

图3 解法2图

生3这时也举手了,说想到了一种简便方法.

生3:解法3 连接AC,如图4所示.

∵l∥m,∴∠KAC+∠JCA=180°.

又∵∠2+∠BAC+∠ACB=180°,

∴∠1+∠2+∠3

=∠2+∠BAC+∠ACB+∠KAC+∠JCA=180°+180°=360°,

∴∠3=360°-135°-95°=130°.

教师点评解法3也是通过构造平行线被第三条直线所截来做的.与解法2相比,由于辅助线并没有改变原图的对称性,解答过程相应的也简单.生3构造了一个△ABC,用到了三角形的内角和.那么能够通过构造一个四边形来解决么?

图4 解法3图

同学们思考了2分钟后,生4举手了,说已经想到了如何利用四边形的内角和来解决了.

生4:解法4 过A点作直线AH交CJ于点H,如图5所示.

∵m∥l,∴∠KAH=∠AHC,

∴∠1+∠2+∠3=∠BAH+∠KAH+∠2+∠3=∠BAH+∠AHC+∠2+∠3=360°(四边形内角和为360°).

教师点评解法4也通过构造平行线被第三条直线所截来做,只是构造了四边形,不仅用了平行线的性质,而且用到了四边形的内角和.相对与解法2来说,作辅助线后更为对称,相应的解法也更简单.与解法3比较,因为AH可以有无数条,所以不如解法3的图形对称.从对称的角度来看,点A与点C是平等的,既然过A点作直线AH可以解这道题,那么,过点C作直线与l相交也必然可以解决这道题,而且过程完全相似,同学们下课后自行解决.

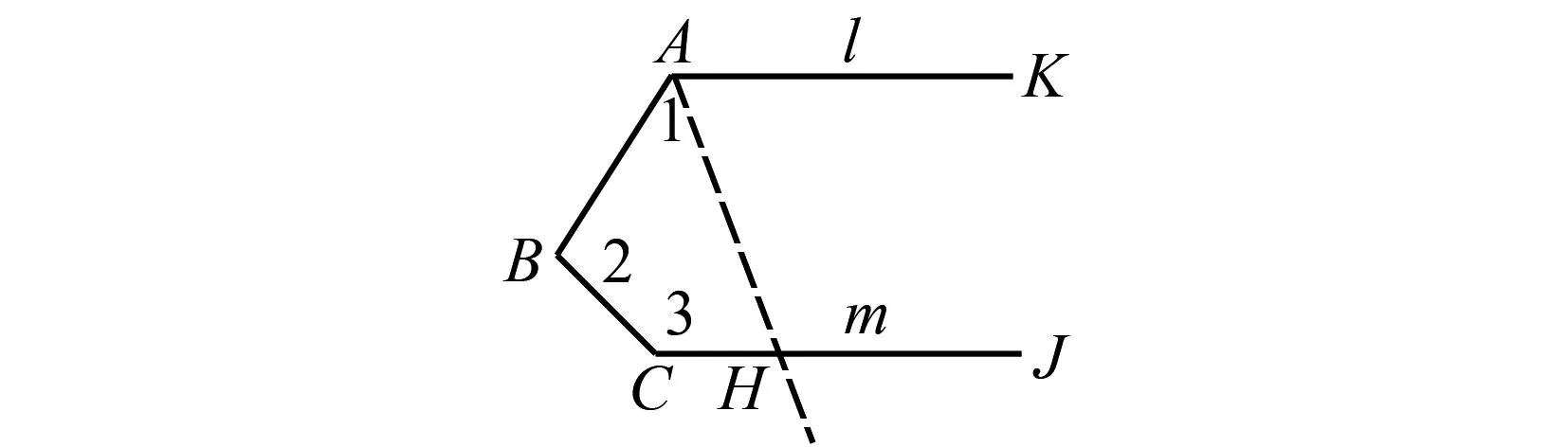
图5 解法4图

这时生5举手了,说自己同样是构造四边形,但这时图象更对称,解答过程更简单.

生5:解法5 作AH∥BC交JC于点H,如图6.

∵BC∥AH,

∴∠2+∠BAH=180°,∠3+∠CHA=180°.

∵l∥m,∴∠KAH=∠CHA,

∴∠1+∠2+∠3=∠KAH+∠BAH+∠2+∠3=∠AHC+∠BAH+∠2+∠3

①

=∠AHC+∠3+∠2+∠BAH

=180°+180°=360°.

∴∠3=360°-135°-95°=130°.

图6 解法5图

教师点评解法5可以像解法4一样,在①式就用四边形内角和得出结论,那过程就如解法3一样.之所以写出上面的解法,是想让同学们知道,解法5的辅助线比解法4更对称美观,所以解答过程可以少用一个知识点(即四边形的内角和).

同样,由于点A与点C是平等的,于是过点C作AB的平行直线与l相交也必然可以解决这道题,而且过程完全相似,下课后同学们自行解决.

这时生6举手说,他想出了一种更为对称的做辅助线的方法.

生6:解法6 作A,B,C关于直线p对称的点A′,B′,C′,连接A′B′,B′C′,如图7所示.

图7 解法6图

∵六边形内角和为(6-2)×180°=720°

∴∠3=360°-135°-95°=130°.

教师点评与前五种解法相比较,解法6的辅助线最对称、最美丽,解答过程相应的也最简洁.

此时教室里响起了一阵热烈的掌声……

3 试题推广

我们下面来看看更为复杂的题:

推广1 如图8所示,已知AB∥CD,求∠A+∠E+∠F+∠G+∠H+∠C.

图8 推广1图

师:用上题中六种方法一一去解它,你会发现,作辅助线后,越具有对称性,解决起来就越简单.下面请同学们用最对称的解法6去解决这个问题.

同学们这时在思考、动笔作辅助线,在计算2分钟后,生7展示了自己的解法.

图9 推广1的解答

师:现在,我们将问题推广到更一般的的情形.

推广2 如图10所示,已知A1X∥AnY,求∠A1+∠A2+……+∠An.

图10 推广2图

同学们在计算,在思考,在作辅助线,经过5分钟后,生8举手了,说自己已经做好了.

图11 推广2的解答

教师点评同学们,今天我们一起学习了平行线中角度问题的计算.我们从最简单的问题开始,各位同学给出了不同的解法,你们都很优秀,很棒,值得表扬,继续努力.经过这堂课的学习,我们不仅会作了各种辅助线,也明白了一个道理:图形越对称,解答越简洁.

数学是美好的,尤其是几何世界里的各种对称问题,希望同学们能领悟对称思想,轻松破解平面几何问题.(叮叮叮……,此时下课铃声响起了)

4 教学反思

通过一节课,解决一道题,引导学生积极思考,最后学生都参与解题,感受到了几何的魅力.问题的设计由浅入深,层层深入,在锻炼学生几何直观的同时,提升了学生直观想象的素养,渗透了对称思想.