浅析高中数学中函数的构造问题
魏明亮
(东莞市东莞中学松山湖学校,广东 东莞 523000)
函数中的构造问题往往是学生很难掌握的内容之一.这类题具有结构独特、技巧性高、综合性强等特点,我们需要熟悉常见的几种函数的构造模型,如果构造合理,将有助于学生快速解题.下面我们将对构造函数的规律方法进行归类总结并举例说明[1].
1 利用f(x)与x构造
例1已知函数f(x)在R上满足f(x)=f(-x),且当x∈(-∞,0]时,f(x)+xf′(x)<0成立,若a=20.6f(20.6),b=ln2f(ln2),c=-3f(-3),则a,b,c的大小关系是什么?
解析已知函数f(x)在R上满足f(x)=f(-x),所以f(x)是偶函数.
构造函数g(x)=xf(x),则g′(x)=f(x)+xf′(x).
由题意可知,当x∈(-∞,0]时,有f(x)+xf′(x)<0成立,即g′(x)<0恒成立,所以g(x)=xf(x)在(-∞,0]上单调递减.
又因为g(x)=xf(x)为奇函数,
所以g(x)在R上单调递减.
因为-3 所以g(-3)>g(ln2)>g(20.6). 即a 因为当x>0时,有xf′(x)-f(x)>0, 所以有h′(x)>0. 因为1<2 即a 推广1若出现nf(x)+xf′(x)形式,则构造函数g(x)=xnf(x)[2]. 例3已知定义在R上的函数f(x)满足f(x)+f′(x)>0,且有f(3)=3,则f(x)>3e3-x的解集为____. 解析构造函数g(x)=exf(x),又因为f(x)>3e3-x,所以f(x)·ex>3e3.即g(x)>g(3). 因为f(x)+f′(x)>0在R上恒成立,所以g′(x)=ex[f(x)+f′(x)]>0在R上恒成立. 所以g(x)=exf(x)在R上单调递增. 又因为g(x)>g(3),所以x>3. 所以f(x)>3e3-x的解集为{x|x>3}. 例4已知可导函数f(x)的导函数为f′(x),若对任意的x∈R,都有f′(x) Af(2) C.e2f(-1)>f(1) D.e2f(-1) 因为对任意的x∈R,都有f′(x) 所以h′(x)<0恒成立. 又因为-1<0<2,根据单调性可知,h(-1)>h(0)>h(2),所以A,C选项正确. 推广3若出现nf(x)+f′(x)形式,则构造函数g(x)=enxf(x). 常用构造的形式有以下几种: (1)g(x)=f(x)sinx,g′(x)=f′(x)sinx+f(x)cosx. (3)g(x)=f(x)cosx,g′(x)=f′(x)cosx-f(x)sinx. 通过观察可以发现这些导函数中都含有f(x),f′(x),sinx,cosx四个相同的量,因为(sinx)′=cosx,(cosx)′=-sinx,所以在f(x)与sinx的构造中,g′(x)出现的是和的形式,h′(x)出现的是差的形式;而在f(x)与cosx的构造中,g′(x)出现的是差的形式,h′(x)出现的是和的形式. 解析根据题意,构造函数g(x)=f(x)sinx,又因为f(x)为奇函数,有 g(-x)=f(-x)sin(-x)=f(x)sinx=g(x). 所以g(x)=f(x)sinx在R上为偶函数. 所以g′(x)=f′(x)sinx+f(x)cosx. 当x∈(0,+∞)时,有f′(x)sinx+f(x)cosx<0恒成立,即g′(x)<0恒成立. 所以g(x)在(0,+∞)上单调递减. 所以h(x)也为偶函数. 这类题型往往是将自变量相同的项放一起,再根据题意构造具体的函数. A.sinα>sinβB.cosα>cosβ C.cosα 即sinβ>cosα,所以选项C正确; 所以选项D正确. 例8若2a+log2a=4b+2log4b,则下列选项正确的是( ). A.a>2bB.a<2bC.a>b2D.a 解析根据指数和对数的运算性质可知 4b+2log4b=22b+log2b. 又因为2a+log2a=4b+2log4b, 即有2a+log2a=22b+log2b. 所以构造函数f(x)=2x+log2x(x>0), 所以f(x)在(0,+∞)上单调递增. 则f(a)=2a+log2a,f(2b)=22b+log22b=22b+log2b+1>22b+log2b=f(a). 即f(2b)>f(a). 因为f(x)在(0,+∞)单调递增,所以2b>a. 即选项B正确. 指对同构经常使用的变换形式有两种,一种是将x变成lnex,然后构造函数;另一种是将x变成elnx,然后构造函数. 例9设a,b都为正数,e为自然对数的底数,若aea A.ab>e B.b>eaC.ab 解析因为b=elnb,所以aea aea 因为a,b都为正数,且blnb>aea>0, 所以lnb>0. 所以构造函数f(x)=xex(x>0). 所以f(a) 又因为f′(x)=ex(x+1)>0在(0,+∞)上恒成立,所以f(x)在(0,+∞)上单调递增. 所以a 所以选项B正确. 数学是一门创造性的艺术,需要极强的数学抽象、逻辑推理能力,巧妙地构造函数在解决数学问题中具有很高的研究和欣赏价值.构造法需要以足够的知识经验为基础,以较强的观察能力、综合运用能力为前提,根据题目的结构特征,对问题进行深入分析,找出已知与所求问题的纽带.虽然构造函数的形式多种多样,但我们可以从尝试解题过程中总结规律,分析结构特征,找到构造函数的依据,从而实现构造.



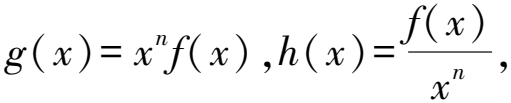

2 利用f(x)与ex构造



3 利用f(x)与sinx,cosx构造












4 构造具体函数关系式












5 同构法构造函数

