大容量推进电机电枢定子建模方法及固有振动特性分析

廖琳, 向阳, 周勇, 潘鹏程

(1.武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063; 2.船舶动力系统运用技术交通行业重点实验室,湖北 武汉 430063; 3.武汉船用电力推进装置研究所,湖北 武汉 430064)

0 引 言

于电力推进舰船而言,推进电机的振动不仅会危害到船舶人员的身心健康,也会降低舰船的声隐身性能,尤其是推进电机发生共振时,会使定子产生较大噪声[1],这对于作战性舰船而言是致命的。振动激励主要来源于电磁激励力和机械激励力,由于船舶推进电机一般为低速旋转设备,其机械激励所致的振动响应比较小,因此本文主要分析电磁激励所致的振动响应。然而,定转子磁场相互作用所产生的电磁激励力一般作用于定子铁磁材料表面,为避免电机定子发生共振以及采取措施来降低其振动,就需要对电机定子的固有频率进行研究分析。

因为电机结构比一般的机械结构要复杂得多,所以国内外诸多学者从多方面对电机的模态进行了研究。WANG Kang[2]同时考虑了轭架厚度、齿深、齿宽、定子线圈、定子外壳和端盖等因素对系统固有频率和模态振型的影响。XIE Ying[3]以1.1 kW的小型异步电动机为样机,采用锤击法进行了模态试验,分析了影响定子固有频率的很多因素。YIN Hongbin[4]提出一种新的定子系统分析模型,该模型可以有效地分析零阶模态,提高模型计算效率。YU Yinquan[5]将定子齿和定子铁心分别建模为悬臂梁和空心圆筒,通过仿真与试验的结果验证了数值计算方法以及仿真模型的正确性和有效性。张镇[6]通过有限元仿真分析获取定子铁心各向同性材料参数并通过锤击法模态试验验证有限元仿真的准确性。代颖、郑清铭等人[7-9]也分析了电动汽车驱动电机机壳、机盖、绕组、铁心对电机模态的影响。此外,也有很多研究者对建模方法进行了研究,其中,王丰华[10]通过有限元法对变压器绕组进行了有限元建模。屈仁浩[11]采用厚壳-梁耦合结构对定子铁心进行简化,计入了定子齿对振动特性的影响。赵斌[12]研究了一种航空发动机整机振动的半实物建模方法,可以对整机的振动特性进行快速准确地分析。张大义[13]利用动力学模型确定整机有限元模型的详细建模方法,并利用该方法对整机的振动特性展开研究。陈云华[14]探讨了电机叠片铁心的建模方法及其振动特性计算方法。ISHIBASHI Fuminori[15]建立了不同复杂程度的电机定子有限元模型来研究线圈和定子齿的不同建模方法对定子整体固有频率的影响。CHAI Feng[16]研究了用于电动汽车轮内电机系统的集中绕组永磁同步电机定子系统的精确建模和模态固有频率。YIN Hongbin[17]建立了小型异步电动机定子铁心和绕组的等效模型来研究材料等效参数对固有频率的影响,结果表明模态固有频率与泊松比成反比和杨氏模量成正比。王平[18]则直接通过实际测试某型发电机组在不同工况下的振动响应与建立的力学模型结合,获取了发电机组轴系的固有频率。

现多数研究学者的电机对象均为小型电机,其定子结构较为简单且材料相对单一,而本文充分考虑大容量推进电机气隙电枢定子的复杂结构及复杂的材料组成。通过缩比定子和全尺寸定子的模态分析,分析两者的相似性。在此基础上,开展全尺寸定子的模态分析,进而获得全尺寸定子的固有频率和振型,并采用机电类比解析法求解定子和定子-绕组模型的固有频率,最后通过模态试验验证定子建模方法,尤其部件之间连接方式的等效处理方法的正确性,为求解大容量推进电机气隙电枢定子固有频率提供新思路。

1 电机定子模态解析理论

对电机定子的模态的解析求解方法,现在多数学者采用机械阻抗法,其原理是机械运动方程与电路中基尔霍夫定律方程进行机电类比而来。机械运动方程与基尔霍夫定律方程如下:

(1)

式中:m为质量;c为阻尼;k为刚度;F(t)为激励力;x(t)为位移;C为电容;E为电源;R为电阻;L为电感;i(t)为电流。机械阻抗法的机电类比关系如表1所示。

表1 机械阻抗法的机电类比关系

以往的研究学者对电机定子铁心的模型等效多数是把定子齿等效成附加质量施加在定子轭上或直接忽略定子齿,且多数学者的研究对象为普通电机,其定子齿和定子轭都是同一种材料且为各向同性材料。但本文研究的电机定子采用气隙电枢结构,其定子齿为复合材料,定子齿、定子轭、线圈为不同的各向异性材料。如此,在验证有限元计算模型建模方法的正确性的同时,也可以验证解析法在定子齿、定子轭、线圈为不同的各向异性材料情况下的适用性。

现将铁心进行等效处理,结合定子的外观,铁心等效为“双圆环”模型。等效示意图如图1所示。

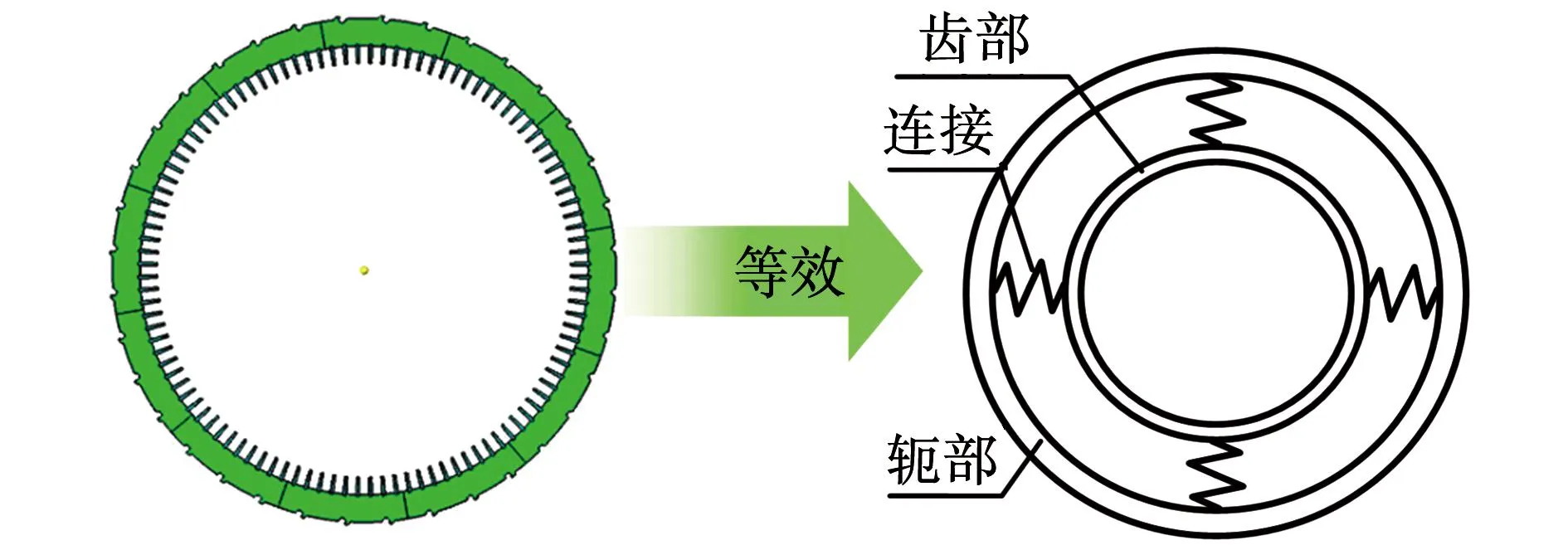
图1 定子模型等效示意图

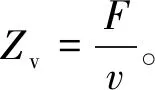
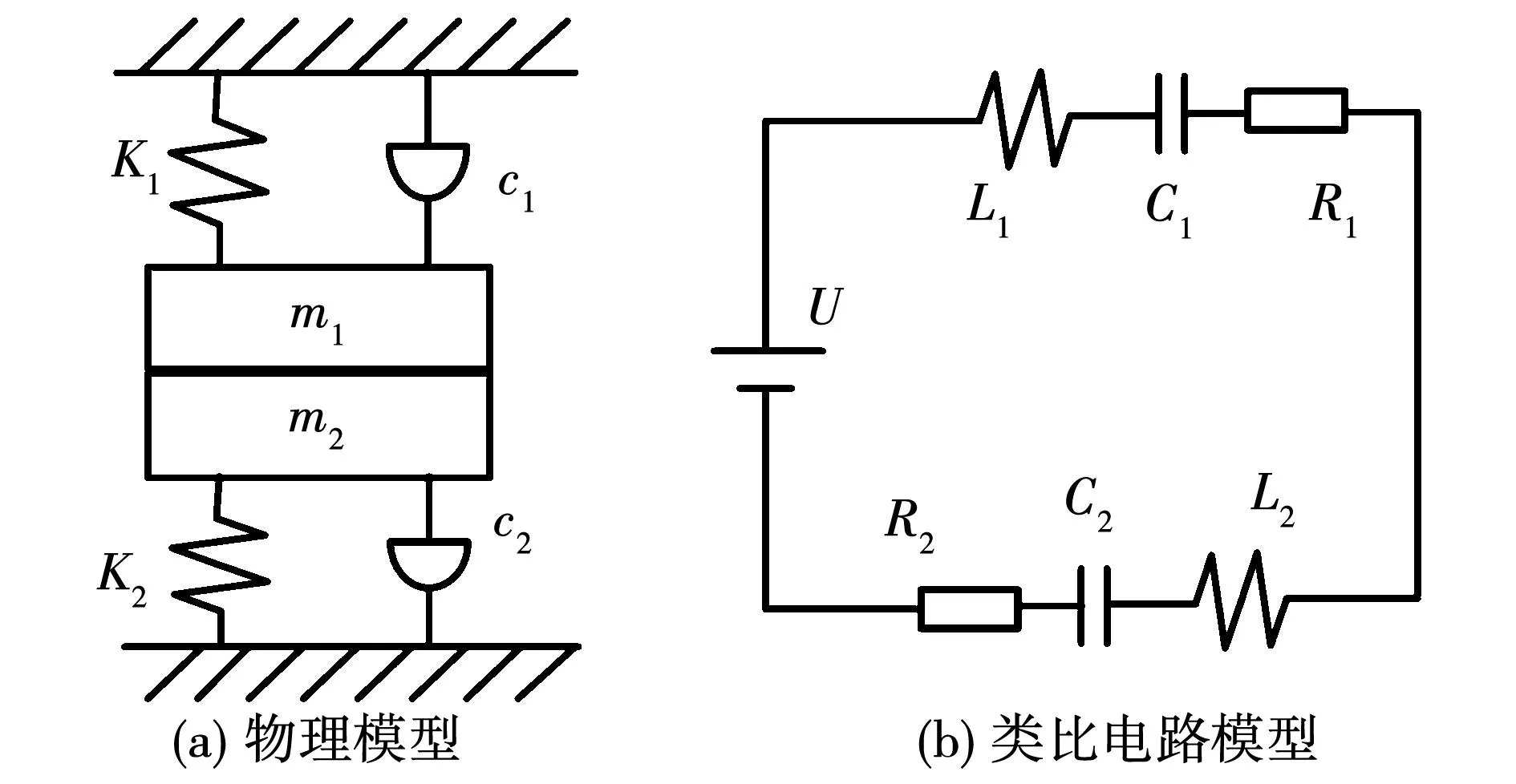
图2 定子铁心机电类比图

在电路中,其电阻求解公式如下:

(2)

式中:Z为总电阻;Z1和Z2均为电阻、电容和电感的总电阻。

再根据表1机电类比原则,当电阻用机械阻抗来表示,式(2)可转化为:

(3)

式中:Zm为机械阻抗,Zm1和Zm2均为刚度、质量和阻尼的总阻抗。

而振动响应参数中的振动速度表示为

(4)

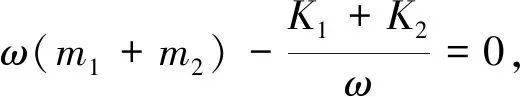
(5)

由文献[19]可知,圆环的质量和刚度表达式为:

(6)

2 定子模态分析

2.1 缩比定子线圈端部简化分析

因为推进电机制造周期长,成本费用高,所以本研究中先建立一个缩比定子的模型,先研究缩比定子的模态振型及其固有频率,并与实验结果进行对比,以验证仿真模型和计算方法的有效性。缩比定子是先将全尺寸定子在周向截取部分,再将截取的部分按一定比例进行缩比,具体缩比尺寸是线圈和定子在轴向方向以1∶2比例缩比,周向长度以2∶3比例缩比,整个缩比过程线圈粗细不变(定子槽尺寸不变),具体缩比示意图如图3所示。

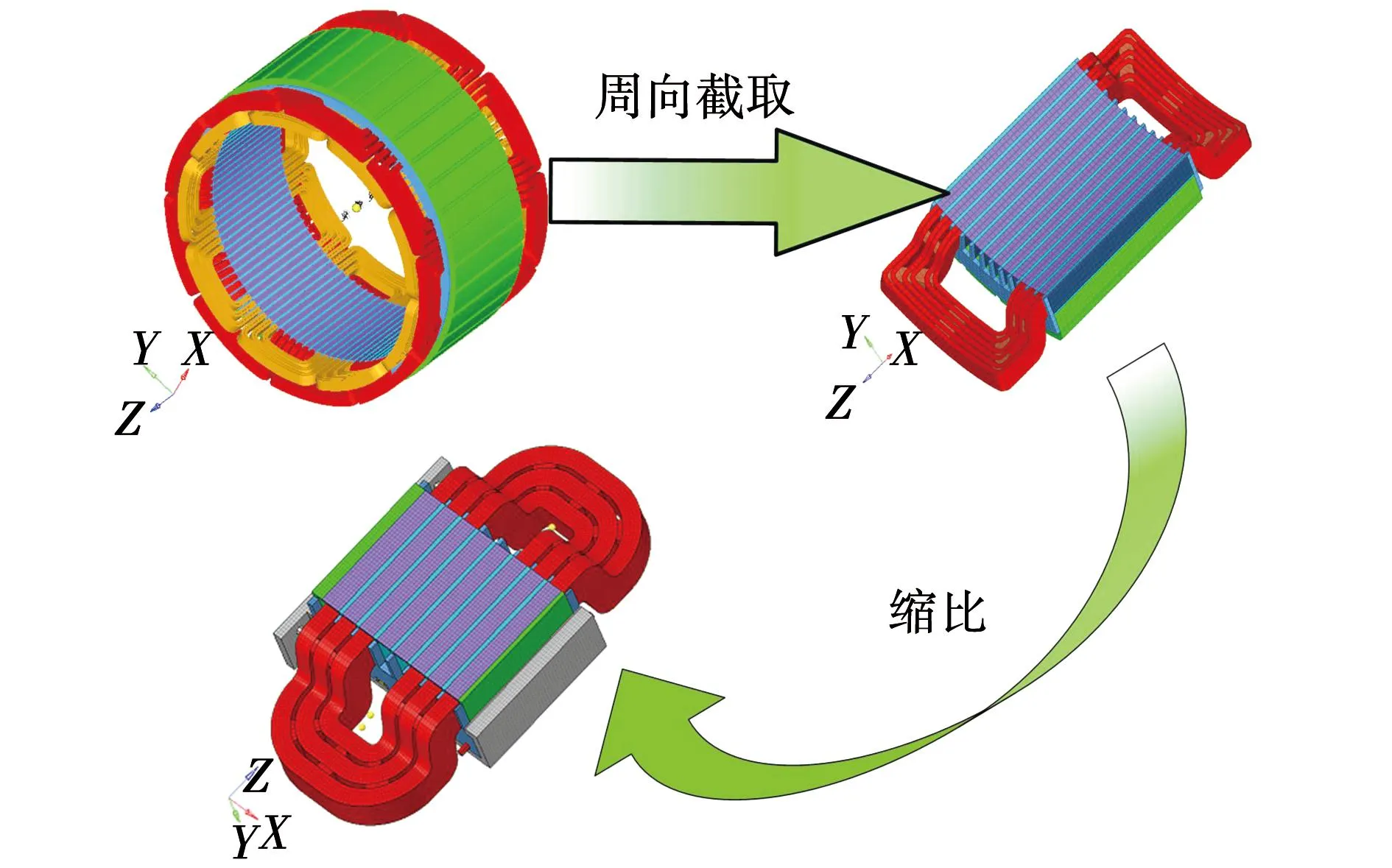
图3 定子缩比示意图

图4展示了缩比定子结构组成,其中紧固螺栓与定子紧固钢是用来紧固铁心的,在建模时简化了螺栓及其对缩比定子的作用,但是,由于绑定线圈的紧固绳对线圈端部局部模态的影响不能忽略,故其不可简化,建立好的有限元模型如图3所示。

图4 缩比定子实物图

在研究电机定子的模态时,因为绕组线圈与线圈之间并非接触状态,在仿真计算时会产生许多绕组端部的局部模态,这样将大大消耗计算资源。因此,需要对端部模型进行简化,忽略绕组端部模型的体积及形状,现提出两种简化方法,一种是等效密度法,通过控制绕组质量,提高直线段线圈的密度;另一种是附加质量法,将端部绕组的质量在Hypermesh前处理软件中以质量点的形式附加在直线圈两端,简化后的模型如图5所示。

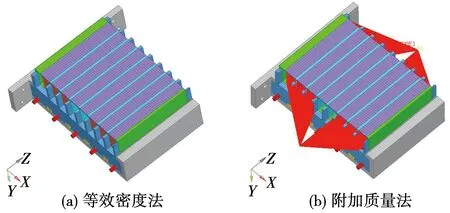
图5 简化模型

对缩比定子分别采用等效密度法、附加质量法以及不简化三种措施处理绕组,各零部件的材料参数如表2所示,在模型分别赋予相应的材料属性后,最后将三种模型导入ANSYS中进行模态仿真计算,计算模态振型阶次以附加质量法的模态振型为参照基准,1～4阶振型图如图6所示(为方便对比,云图显示均将绕组端部模型隐藏)。

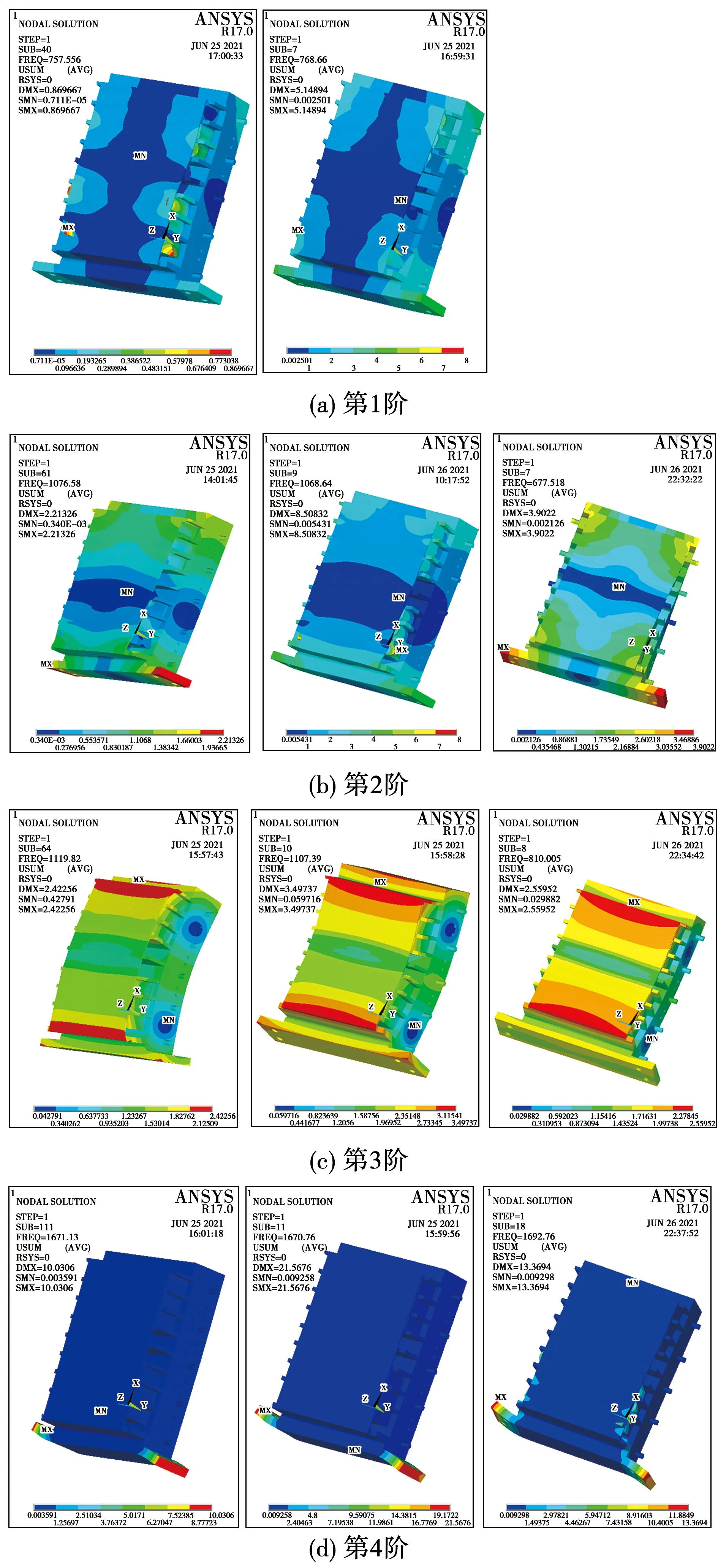
图6 绕组端部原模型(左)、附加质量(中)、等效密度(右)振型图

表2 各零部件材料属性

绕组端部在三种不同状态下各阶次的频率如表3所示。从表中可看出采用附加质量法处理绕组端部所建立的定子模型与原模型的固有频率误差较小,而利用等效密度法建立的定子模型的固有频率与原模型只在第4、5阶的固有频率相差较小,在第2、3阶相差较大。此外,等效密度法建立的定子模型会发生阶次错乱及个别阶次消失的现象,主要原因是采用等效密度法建立的绕组其密度是均匀的,破坏了原有结构的质量分布规律。与此同时,也侧面说明附加质量法建立绕组端部模型的有效性。

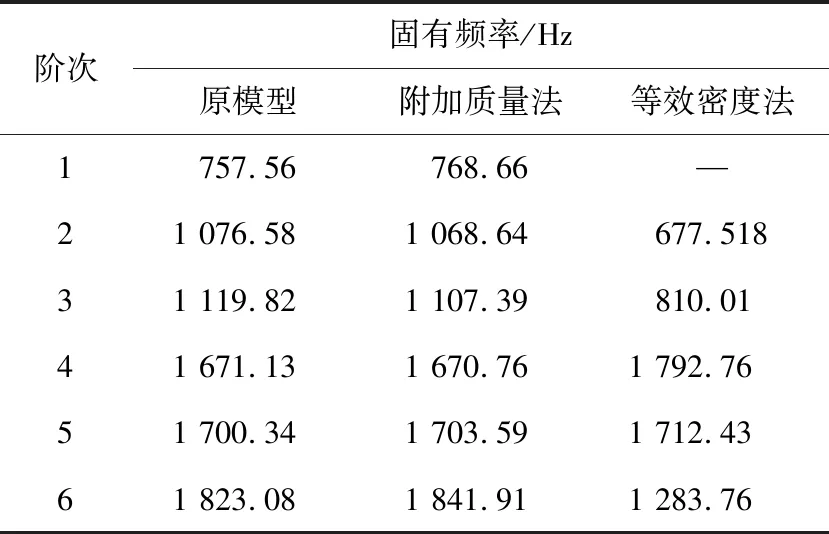
表3 绕组端部在三种不同状态下固有频率

2.2 缩比定子与全尺寸定子相关性研究

在对缩比定子进行建模方法分析后可知,采用附加质量建立绕组端部模型相较等效密度法更为准确。同时,为验证定子有限元分析模型的建立方法,尤其部件之间连接方式的等效处理方法,并在此基础上,开展全尺寸定子的模态分析,进而获得全尺寸定子的固有频率和振型,可对缩比定子与全尺寸定子进行相关性研究。

先分别建立缩比定子和全尺寸定子的周向截断部分有限元模型,对于相同的零部件赋予相同的材料属性,在全尺寸定子的周向截断模型线圈端部位置建立绑定绳的模型,最后对二者分别进行模态仿真计算,计算结果的前4阶振型图如图7所示。

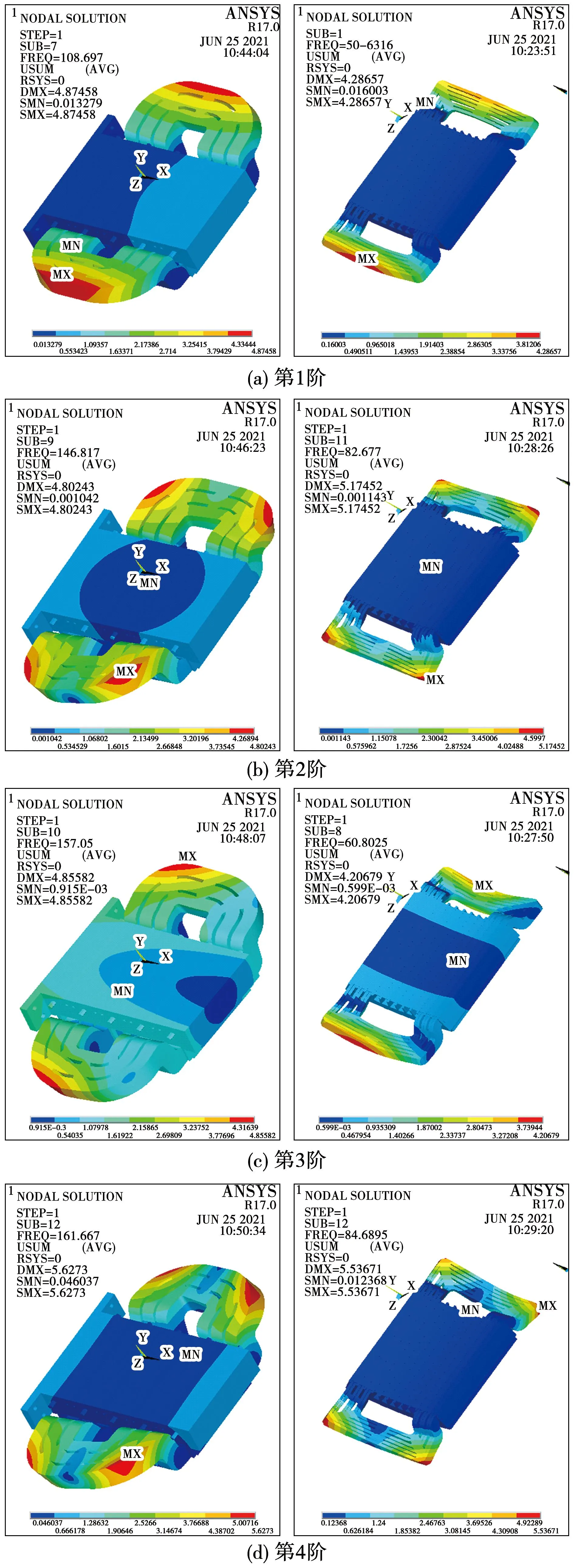
图7 缩比定子(左)和全尺寸定子截断部分(右)振型图

从振型图可以看出,在同一阶次下,缩比定子和全尺寸定子截断部分具有相似的振型,不仅如此,在任一相同阶次下,这二者的最大位移也发生在相同的位置。由此可以说明,通过缩比定子来研究电机定子的材料参数、建模方法是可行的,这对于全尺寸定子的分析具有借鉴意义。

2.3 全尺寸纯定子模态分析

以往的研究学者对电机定子铁心的模型等效多数是把定子齿等效成附加质量施加在定子轭上或直接忽略定子齿,这是造成误差的主要原因。在此,将定子齿的影响考虑进去,将纯定子考虑成“双圆环”模型进行等效。等效后,根据模型的几何尺寸,首先确定定子轭外径为1 303 mm,再由等效前后体积不变原则,推算出轭部等效模型内径为1 167 mm。因为定子齿与轭部之间发生的切向位移几乎为0,若将等效模型理想化,定子齿与轭部之间紧密连接,即二者之间的刚度为0。如此,等效模型中定子齿的外径与轭部内径相等,为1 167 mm,再推算出定子齿的内径为1 146 mm,相关参数代入式(6),求解其模态解析解。

建立定子模型的有限元模型,在赋予相关材料参数后,使用有限元法对其进行模态计算,其振型如图8所示,并将求解模态的有限元解和解析解的结果进行对比,对比结果如表4所示。

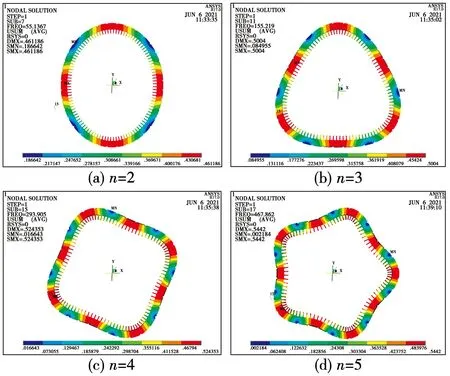
图8 全尺寸定子振型图

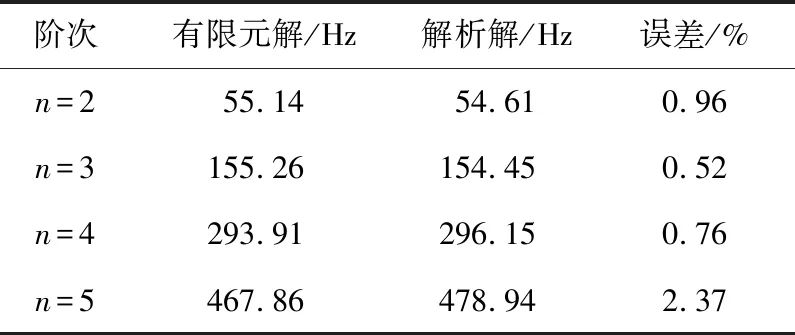
表4 不同求解方法下模态结果对比

由表5可知,无论是定子轭还是纯铁心,其误差均会随着模态阶数的增长而增大,在径向模态阶数范围为2≤n≤5时,定子轭的最大误差不超过5%,纯铁心的最大误差不超过3%,这说明了本文有限元模型建模方法的有效性以及“双圆环”解析模型使用的机电类比解析法同样适用于定子铁心为各向异性材料的情况。为后续研究定子-绕组系统的模态提供了依据。

表5 定子-绕组固有频率有限元解

2.4 全尺寸定子-绕组模态分析

根据缩比定子绕组端部建模方法的分析研究和缩比定子和全尺寸定子的相似性,在对定子-绕组进行有限元模态分析时,需要在前处理软件Hypermesh中对全尺寸定子绕组采用附加质量法简化端部。简化方式要在两边的绕组端部分别建立其质心点,用reb3单元连接质心与线圈直线端节点,在质心点上建立mass21单元,并给质量单元mass21赋予端部质量,简化后的定子如图9所示。

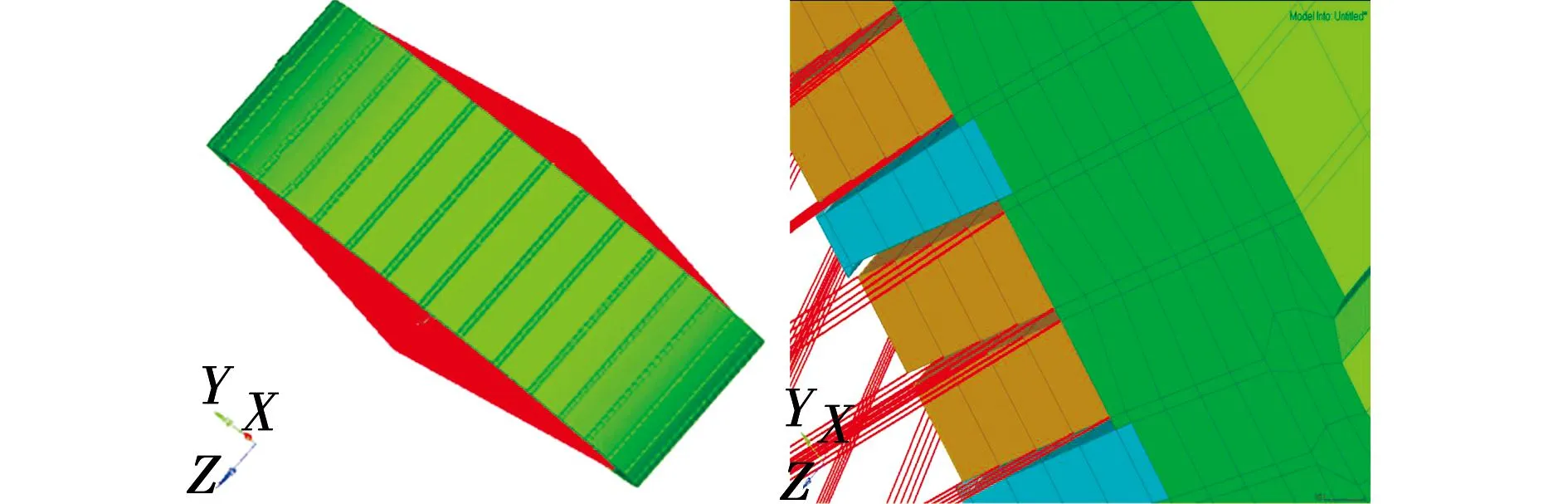
图9 定子的简化示意图

在前处理软件中处理好线圈的模型简化后,并赋予各个材料的属性,将定子-绕组有限元模型导入到ANSYS APDL中进行模态仿真计算,计算结果如表5所示。同时,根据解析理论,可将定子-绕组等效为“三圆环”模型。同时,定子齿与线圈间的连接依旧假想为这两者间不发生切向位移,结合机电类比求解定子铁心径向模态频率推导过程可知,其固有频率如下:

(7)

式中:R3为线圈圆环的平均半径,单位为m;m3为线圈的质量,单位为kg;h3为线圈圆环的厚度,单位为m;E3为线圈弹性模量,单位为Pa,因为在周向上,线圈不同方向的弹性模量不同,即Ex≠Ey,在这E3可取两者平均值。

线圈圆环外径等于定子齿圆环的内径,为1 146 mm,再根据等效前后体积不变可推算出线圈圆环内径为1 069 mm,将定子-绕组模型的相关参数代入式(7),求得定子-绕组的模态解析解。同时,为分析材料的各向异性特点对其模态的影响,对材料属性二次赋予,将3种材料中的弹性模量以E=(Ex+Ey)/2进行近似,再将所求解析解与定子-绕组模型的有限元解进行对比,对比结果如表6所示。

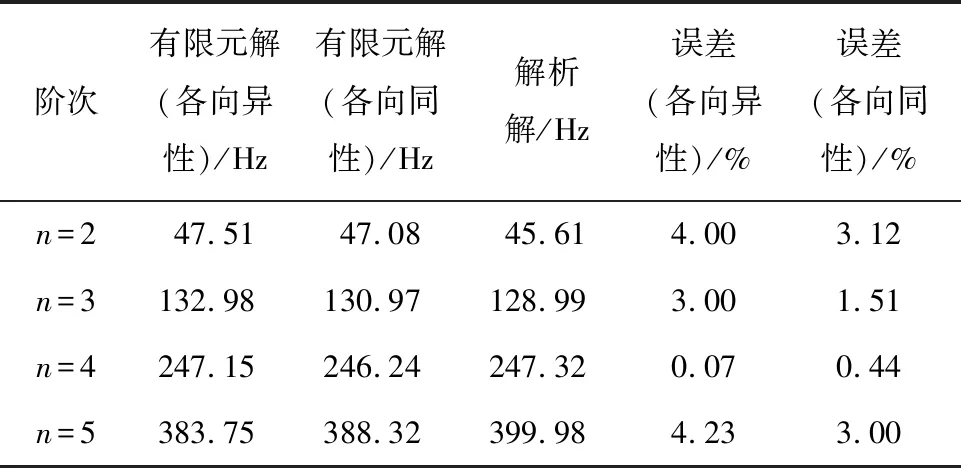
表6 不同求解方法下定子-绕组模态结果对比

由表中数据可知,解析解与有限元解之间的误差也是随着模态阶数的增大呈现先增大后减小的趋势,且通过对比各向同性和各向异性材料定子-绕组仿真值与解析解的相对误差,两者较为接近,说明各向异性对仿真结果影响较小。从材料为各向异性的结果来看,相比纯铁心“双圆环”等效模型,定子-绕组“三圆环”等效模型的有限元 解与解析解误差略大主要原因为:定子-绕组“三圆环”等效模型中,定子齿圆环与线圈圆环间的无切向位移假设相较于纯铁心“双圆环”等效模型有些许偏离实际情况,且在进行解析计算时以附加质量的形式代替定子-绕组有限元模型中绕组端部实体模型,但在定子-绕组模型的径向模态阶数范围为2≤n≤5时,这两者的误差不超过5%,在一定程度上也验证了定子-绕组的“三圆环”等效模型的有效性。

3 参数灵敏度分析

3.1 材料参数影响分析

无论是在对推进电机的解析建模还是仿真计算过程中,材料参数对其固有频率有着不同程度的影响,包括材料密度、弹性模量和泊松比三要素,为进一步分析这几种参数对定子模态频率的影响,现在以定子轭部为例,进行参数敏感度分析。

虽然定子轭部材料为各项异型,但是本文分析的频率为径向模态频率,该类型频率只与x和y方向的材料参数有较大关系,而定子轭部xoy平面上的材料参数(弹性模量)相等,所以在讨论弹性模量对定子径向模态频率影响时,应同时考虑Ex和Ey的变化;对于密度和泊松比则无方向区别,在讨论一个参数变化时,控制其他两个变量不变,通过仿真计算得到三者对推进电机定子径向模态的影响如图10所示。

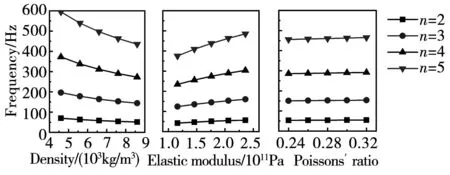
图10 电机径向模态参数影响分析

从图中可以很明显看出,材料密度和弹性模量对定子径向模态影响较大,而泊松比则基本无影响,且该影响(绝对差值)对低阶次模态频率影响较小,还会随着阶次的提高而变大。

3.2 复合参数影响分析

对于解析模型而言,定子轭“单圆环”解析模型径向模态频率表达式为

(8)

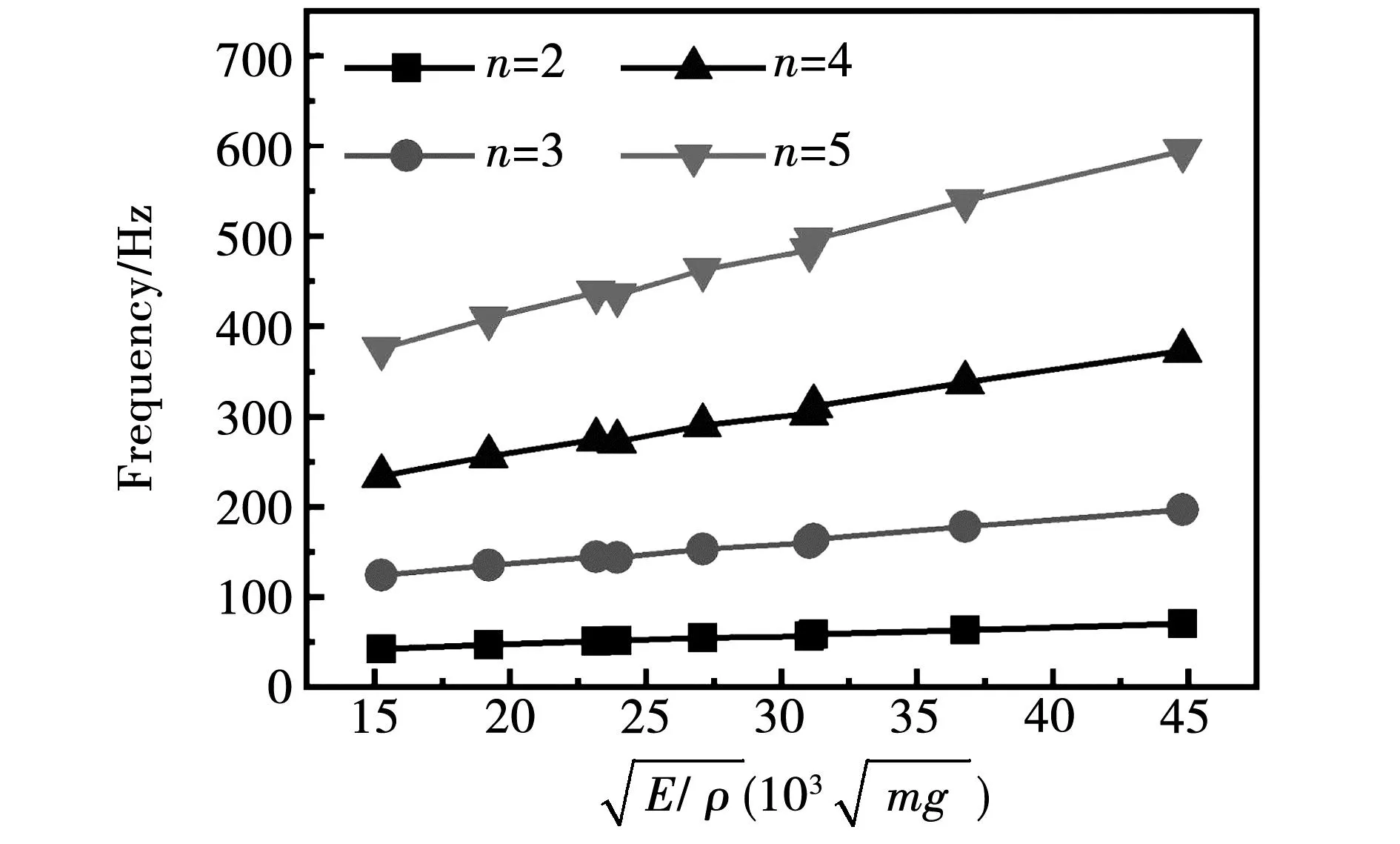
图11 参数对电机定子径向模态的影响

3.3 其他参数无关性分析

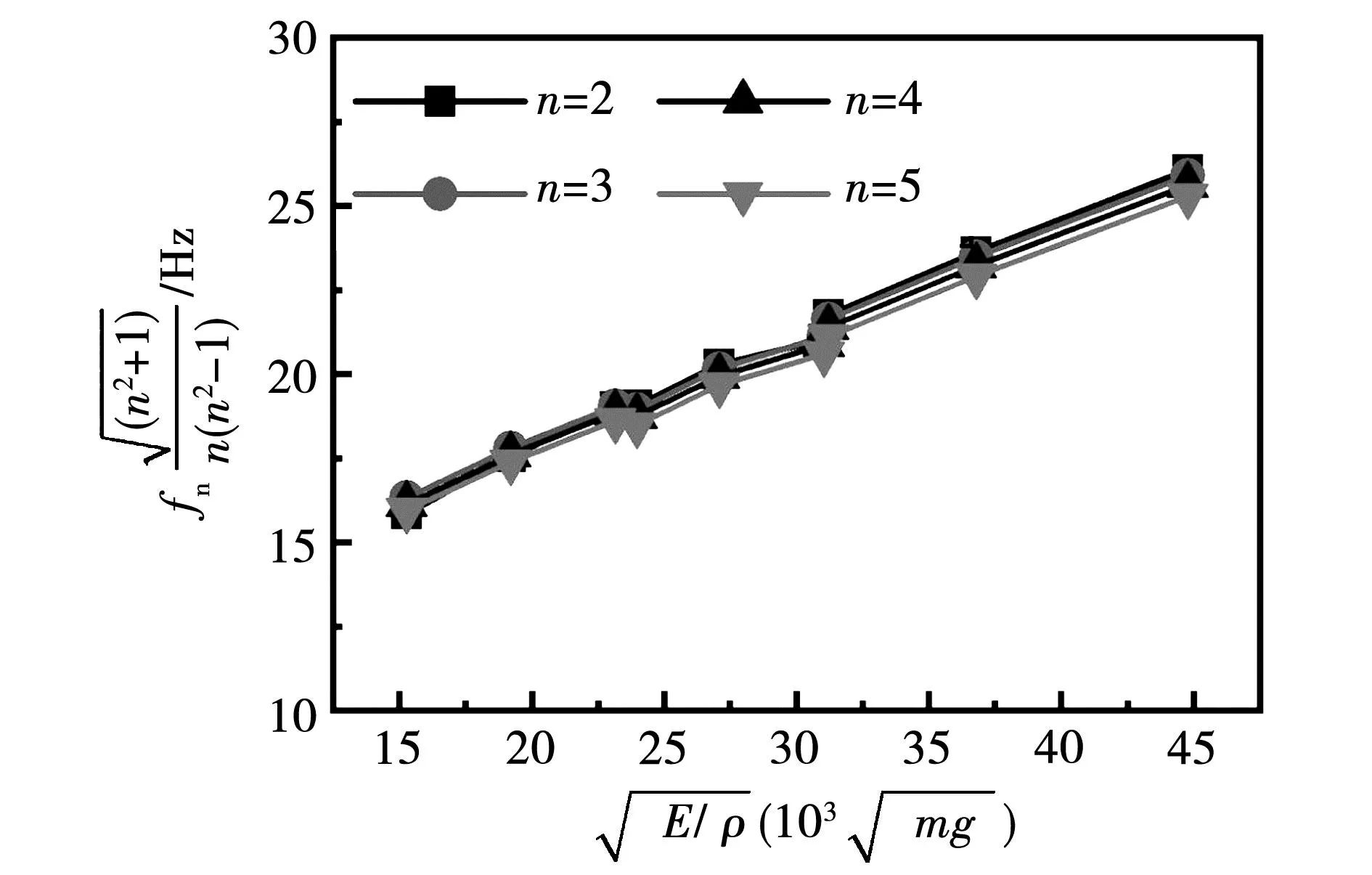
图12 其他参数无关性分析

从图中可以明显看出,各阶次下的变化曲线几乎重合,这意味着电机定子径向模态只受弹性模量和密度两因素的影响,与其他参数无关。

4 试验验证

为了进一步验证建模过程中一些零部件简化的准确性以及建模方法的有效性,对缩比定子采用锤击法进行模态试验。数据采集采用DHDAS测试系统,传感器采用Lance加速度传感器,力锤型号为LC-60KN,测试时采用悬挂的方式使缩比定子处于自由状态,测试现场图如图13所示。

图13 测试现场图

在测试时,由于测试系统为32通道,但测定总共设计了132个测点,所以需要分批次测量,并且要用到交换机连接网线以同时启动32个通道,整个测试系统示意图如图14所示。将模态测试结果与有限元仿真结果进行对比,对比结果如表7所示。

图14 测试系统示意图

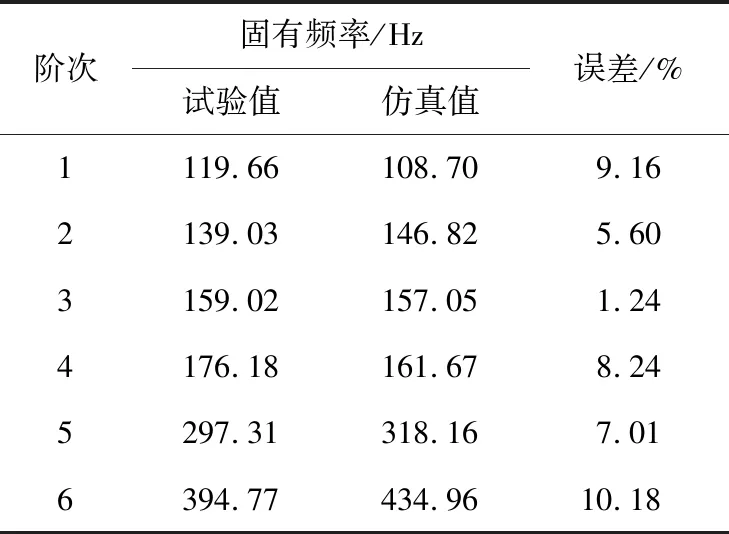
表7 缩比定子固有频率

从表中可看出,虽然仿真与试验存在一定误差,有个别阶次的固有频率仿真值与试验值误差略超过10%,误差来源于线圈与定子铁心之间和铁心与紧固刚之间并非完全刚性连接,其余阶次误差范围均在10%以内,同时说明了前文建模方法与计算方法的有效性。

5 结 论

本文通过建立缩比定子模型及对其进行模态测试与仿真试验,研究了推进电机缩比气隙电枢定子与全尺寸气隙电枢定子之间的相似性,并采用机电类比解析法求解了定子和定子-绕组模型的固有频率,并对材料参数进行了灵敏度分析,得出以下结论:

1)用附加质量法对缩比定子绕组端部模型建模,与原模型的固有频率最大误差为1.73%,相较于等效密度法更准确,同时也说明质量的分布对于模态计算有较大的影响。

2)缩比定子与全尺寸定子之间存在一定的相似性,通过缩比定子来研究电机定子的材料参数、建模方法是可行的。

3)机电类比解析法将定子和定子-绕组模型等效为圆环模型在n≤5的阶次范围内解析解与仿真解最大误差分别为2.37%和4.32%,说明解析法可以有效快速地计算出这二者的模态,为大型推进电机定子的模态计算提供了新方法。