基于机器学习正则化理论的永磁同步电机转矩跟踪型MTPA控制方法

漆星, 郑常宝, 曹文平, 张倩

(安徽大学 电气学院,安徽 合肥 230601)

0 引 言

内置式永磁同步电机(interior permanent magnet synchronous motor,IPMSM)由于其高效、高功率密度、宽调速范围等优点,在工业控制领域中大量应用。IPMSM本身具有的凸极性可以产生磁阻转矩,相较于表贴式永磁电机具有更高的动力输出。然而,IPMSM的凸极性会使得电机内部的交、直轴电感不一致,进而引出IPMSM控制中的交、直轴电流分配问题。在实际工程中,为减小损耗、最大限度地利用磁阻转矩,一般采用最大转矩电流比(maximum torque per ampere,MTPA)方式对IPMSM中的交、直轴电流进行分配[1]。

近年来,一些特定领域的高速发展对IPMSM中的MTPA控制策略提出新的需求。例如,在电动汽车、数控机床等应用领域,其IPMSM中的MTPA控制策略不仅要求能够找出满足最大转矩电流比的最优交-直轴电流,还要求能够精确地跟踪转矩指令,称为转矩跟踪型MTPA控制。在已知给定转矩指令的条件下,如何使得电机的实际输出转矩与指令转矩保持一致,也是转矩跟踪型MTPA控制策略研究中需要解决的问题。

现如今主流的MTPA方法主要分为模型驱动法和数据驱动法两类。模型驱动方法是利用电机本身的电感、磁链等模型,或者是利用谐波注入、在线搜索等手段,通过公式解析的方法推导出IPMSM中交、直轴电流的最优设定值[2-4]。模型驱动法具有结构简单、容易实现和易于解释的特性,其缺点在于使用的是电机的近似模型而非精确模型,往往无法克服模型误差的问题,在处理电感中的交叉饱和效应时难度较大[5-6],从而导致实际转矩跟踪精度下降,往往不能满足转矩跟踪型MTPA方法的要求。

另一类MTPA方法主要基于电机实测数据,称为数据驱动法,具体而言,是搜集电机的有限元分析数据[7]或者电机离线测试数据[8],再通过数据拟合或数据挖掘的方法建立MTPA问题的数据模型。数据驱动的方法不依赖电机的近似模型,并且在数据挖掘的过程中已经考虑了由于电感磁饱和或交叉磁饱和而引起的非线性,因此转矩跟踪精度优于模型驱动方法。不过与模型驱动法使用的解析表达不同,现有的数据驱动方法大多使用非解析的隐式表达,例如神经网络、随机森林、支持向量机等[9-11],或者以网格搜索的形式建立“转速-转矩-电流”形式查找表并存储在电机控制器的MCU中[12]。相较于模型驱动方法,数据驱动方法虽然具有较高的转矩精度,但是存在数据结构复杂、算法结果不易解释等缺陷。

以上两种方法都具有各自的优缺点,而迄今为止还没有一种方法能够融合两种方法之间的优势,从而实现算法简洁、结果精确的转矩跟踪型MTPA控制。基于此,本文借鉴机器学习理论中的正则化思想,研究一种将MTPA问题转化成机器学习理论中的L1、L2正则化问题的方法。首先将MTPA控制问题等效为机器学习中的L2正则问题,再对上述L2正则问题中的转矩约束条件进行L1正则转矩建模,最后使用拉格朗日对偶方法,对正则化后的MTPA问题进行优化求解。理论分析和实验结果表明,将IPMSM中的MTPA问题转化成机器学习中的正则化问题后,可以得到兼顾最大转矩电流比和高转矩跟踪精度的最优解,从而满足转矩跟踪型MTPA的需求。本文方法结构简单、模型易于解释,又避免由于模型误差和电感饱和特性而造成的性能降低,从而融合模型驱动方法和数据驱动方法的优势。

1 IPMSM的MTPA控制和机器学习正则化理论

1.1 IPMSM的数学模型与MTPA控制

假设IPMSM模型为线性,即交、直轴电感为恒值,并忽略温度变化引起的电阻变化,则IPMSM在d-q轴坐标系下的电压方程为:

(1)

式中:usd、usq为d-q轴电压;isd、isq为d-q轴电流;Rs为定子电阻;ωe为电角频率;ψsd和ψsq分别为d-q轴磁链,其中:

(2)

其中:Ld、Lq分别为d、q轴电感;ψf为永磁体磁链。

IPMSM的转矩方程为

(3)

式中np为电机的极对数。

MTPA 控制方法是IPMSM控制中较为常用的方法, 其目的是以最小铜损实现IPMSM的最大转矩控制,以输出电流最小为优化目标,可将传统的模型驱动MTPA控制方法用数学描述为:

(4)

对式(4)使用拉格朗日乘子法,可将其等效为

(5)

式中:L(·)表示拉格朗日函数;λ为拉格朗日乘子。

对式(5)求偏导,最终可得最优的d-q轴电流的设定值为:

(6)

可以看出,使用式(3)～式(6)的MTPA方法需要预知电机的转矩模型,以及ψf、Ld和Lq等模型参数,考虑到模型的非线性和电感的交叉饱和特性,实际电机运行过程中ψf、Ld和Lq的精确值往往难以获得,因此模型驱动方法通常只能获得最优电流值的近似解而非精确解,从而影响到最终的转矩跟踪精度。同时,传统的MTPA控制问题为转矩开环的电流分配问题。例如,从式(3)～式(6)可知,isd、isq的选取只与实际输出转矩Te有关,与指令转矩无关,因此不能构成指令转矩闭环的转矩跟踪控制。

1.2 机器学习中的正则化理论

由于本文方法是建立在机器学习中的正则化理论上的,因此本节对正则化理论进行简要介绍。机器学习中的正则化理论是通过最小化系数矩阵来降低学习器训练过程中存在的泛化误差,防止学习器陷入过拟合。同时,正则化理论可将特征选择和学习器的训练过程融为一体,即在学习器训练过程中自动进行特征选择[13]。

给定数据集D={x,y∈R|(x1,y1),…,(xn,yn)},以线性回归模型为例,未正则化时,学习器的最小化训练损失函数为

(7)

而正则化后,学习器的最小化训练损失函数为

(8)

式中:w=[w1,w2,…,wn]为线性回归模型的系数矩阵;‖·‖P表示P范数;λ为拉格朗日乘子。可以发现,加入正则项后,使得系数矩阵w最小也是其优化训练损失函数的目标。

称P=1时的式(8)求解问题为L1正则问题,其中系数矩阵w的L1范数为

‖w‖1=|w1|+|w2|+…+|wn|。

(9)

称P=2时的式(8)求解问题为L2正则问题,其中系数矩阵w的L2范数为

(10)

L1正则和L2正则在特征选择上的区别如图1所示,其中椭圆和菱形(圆形)区域的切点就是目标函数的最优解。可以发现L1正则和L2正则都有助于降低过拟合的风险,然而L1正则中,均方误差(mean square error,MSE)等高线和L1范数的交点大多在某项坐标轴上,这表明L1正则更倾向于获得多项系数为0的稀疏模型,以使模型具有结构简洁、易于解释的特性;而在L2正则中, MSE等高线和L2范数的交点大多不在坐标轴上,这表明L2正则更倾向于获得各项系数尽可能小的精确模型,以使模型具有高精确性[14]。在本文的方法中,将会综合使用L1和L2正则技巧,从而使得本文方法兼具简洁性、易解释性和高精确性的优势。

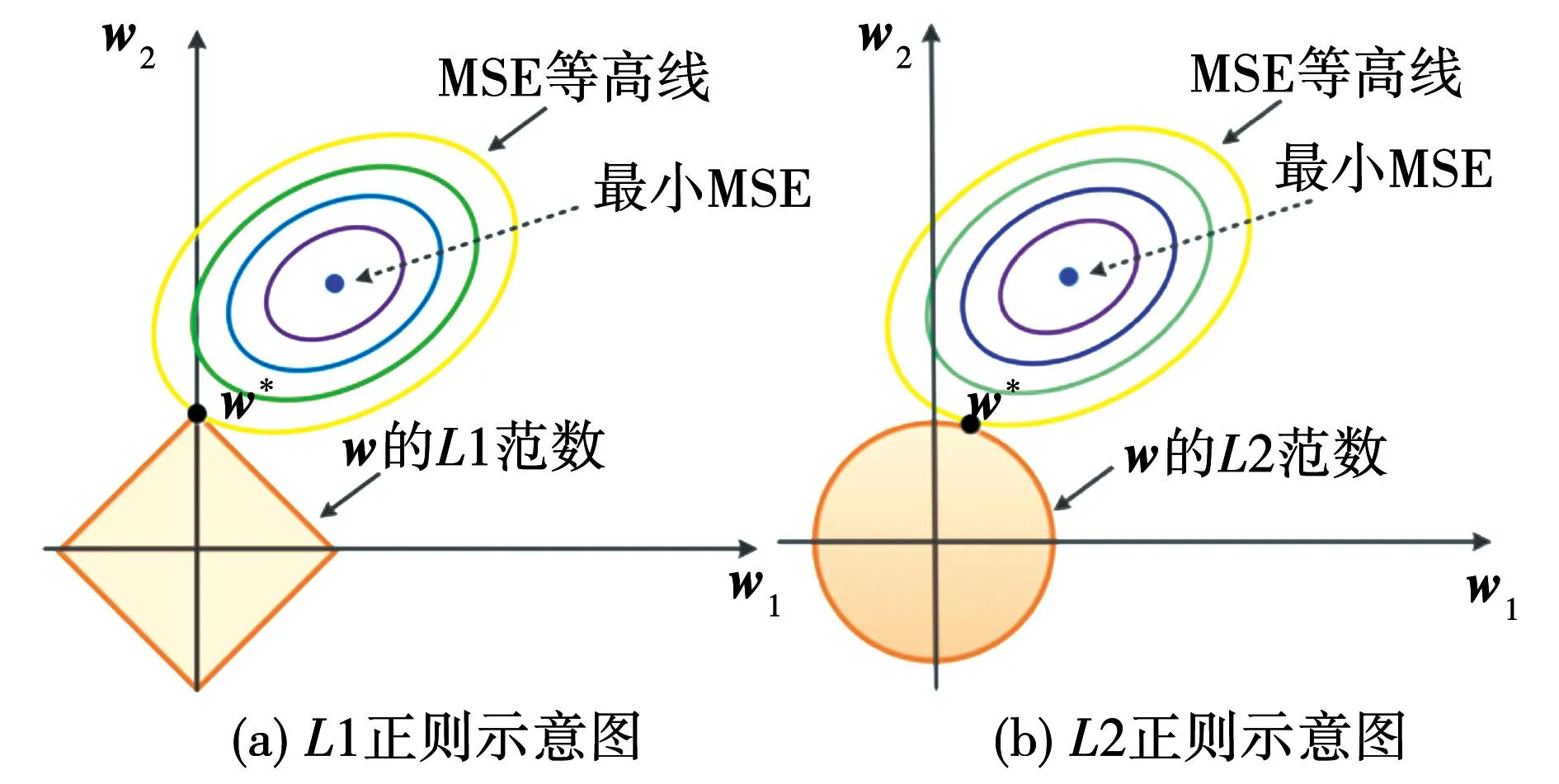
图1 L1和L2正则化示意图

2 基于正则化理论MTPA控制方法

2.1 转化为L1和L2正则问题的MTPA控制方法

本节将IPMSM的MTPA问题转化为L1和L2正则化问题,并给出方法的总体框架。若考虑转矩指令跟踪精度的要求,则可将转矩跟踪精度作为优化目标,即IPMSM的转矩跟踪MTPA问题可重写为以转矩跟踪精度为目标的电流最优分配问题,即:

(11)

再使用拉格朗日松弛法,可得式(11)的等价形式为

(12)

至此得到了式(8)所示的MTPA的L2正则等价形式,根据1.2节正则项的定义,其中转矩误差项MSE保证了转矩跟踪精度最优特性,而正则项L2REG使得输出电流最小,使其具有最大转矩电流比特性,从而兼具了转矩跟踪精度和MTPA的要求。

事实上,可将式(3)代入式(12)中的约束项Te=f(is),则可将式(12)中转化为模型驱动的转矩跟踪型MTPA问题进行求解。然而,根据1.1节分析,由于ψf、Ld和Lq的参数真实值往往未知,并且ψf、Ld和Lq还可能存在着非线性和交叉饱和问题,使用模型驱动求解方法往往无法获得理想的转矩跟踪精度。因此,本文将采用数据驱动的L1正则化方法进行转矩模型Te=f(is)的求解。由此得到的最终模型为:

(13)

或简写成

(14)

由此,便可以将转矩跟踪型MTPA控制问题转化成机器学习中的L1、L2正则化问题。其中L2正则可以保证算法结果的精确性,而L1正则可以保证算法结构的简洁性和可解释性。

在实践中,本文研究方法的实际操作可分为离线测试阶段和在线调节阶段,如图2所示。具体步骤为:

图2 基于L1、L2正则化问题的MTPA控制框图

1)在离线阶段采集电机的测试数据,包括不同转速下的转矩Te、d轴电流isd和q轴电流isq;

2)将步骤1中采集的数据存储至数据池中,并建立电机转矩的L1正则模型,具体方法由2.2节给出;

3)将步骤2中建立的L1正则转矩模型代入式(14)中的L2正则MTPA问题,并使用拉格朗日对偶原理求解最优拉格朗日乘子λ,具体方法由2.3节给出;

4)在求出步骤3中的最优λ后,使用优化理论完成最优isd和isq的求解,从而实现在线的转矩跟踪型MTPA控制。

2.2 基于L1正则问题的转矩建模

本节分析式(13)、式(14)中,基于L1正则化理论的转矩建模方法。首先借鉴传统转矩模型的结构建立字典库,再基于字典库,采用L1正则化理论中的LASSO回归方法建立结构最优的数据驱动转矩模型,使得建立的转矩模型兼具精确性、简洁性和可解释性。具体步骤为:

1)采集电机的台架测试数据{Te,isd,isq};

2)建立数据驱动的转矩模型结构为Te=ΞΘ(is),其中,Ξ=[ξ1,…,ξn]为模型系数矩阵,Θ(is)为在转矩模型中有可能出现的isd、isq的组合,称之为字典库[15]。借鉴式(3)中传统的转矩模型结构,认为Θ(is)中的字典复杂度不会超过is的二次型结构,即

(15)

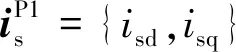
Te=ΞΘ(is)=

(16)

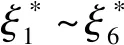
λ‖is‖1}。

(17)

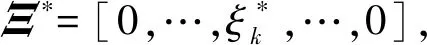
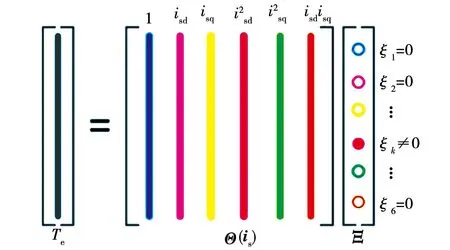
图3 基于L1正则化的转矩建模

4)求得最优稀疏系数矩阵Ξ*后,代入式(14),最终可将IPMSM的MTPA问题转化为

(18)

式中:is=(isd,isq)为需要求解的d-q轴电流值;λ为未知参数。

2.3 使用拉格朗日对偶求解最优参数

对式(18)进行分析可知,λ的选择会影响到最优isd、isq的求解:过低的λ值会导致过大的is绝对值,而过高的λ值会导致过大的转矩跟踪误差,如图4所示。因此在求解最优isd、isq前,须先确定最优λ值,记为λ*。

图4 λ的选择对最优isd、isq的影响

针对上述问题,本节使用拉格朗日对偶方法[17]求解λ*,步骤如下:

首先引入拉格朗日函数L(is,λ,ismax),表达式为

(19)

则可将式(18)重写为

MTPA≜minisminλL(is,λ,ismax)。

(20)

则与之对应的拉格朗日对偶问题为

MTPA≜minisminλL(is,λ,ismax)≜

minλminisL(is,λ,ismax)=

(21)

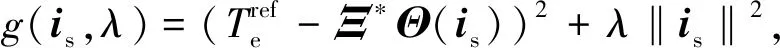
(22)

对式(22)求解可得isd、isq基于λ的表达式,记为isd(λ)和isq(λ)。再将isd(λ)和isq(λ)代入式(18),可将式(18)转化为最优λ*求解问题,表示为

(23)

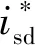
3 仿真算例分析

为能直观地说明本文方法的操作步骤,并验证本文方法的有效性,在MATLAB/Simulink仿真环境下进行实际算例演示,仿真电机参数如表1所示。在本节中,分别考虑Ld、Lq为恒参数值和变参数值这两种情况进行算例分析。

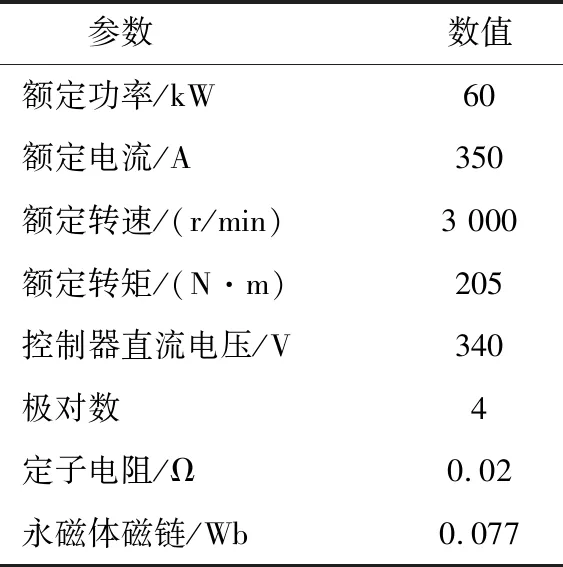
表1 电机参数

3.1 恒Ld、Lq参数值的MTPA控制策略

假定Ld、Lq数值不会随着isd、isq变化,在仿真模型中设Ld=0.000 33 H、Lq=0.000 82 H,根据式(3)得到传统的转矩模型为

Te=0.462isq-0.002 9isdisq。

(24)

在本节的仿真中,不考虑电机的数学模型和转矩模型,而直接让电机运行于不同的转速和转矩,采集转矩Te、d轴电流isd以及q轴电流isq数据,并使用式(16)中的L1正则方法进行Te=ΞΘ(is)求解,解得Te的模型为

0.453 9isq-0.002 9isdisq。

(25)

将式(25)与式(24)中的传统转矩模型Te=0.462isq-0.002 9isdisq进行比较,可以发现,L1正则方法虽然是数据驱动的模型,但是和传统的转矩模型相比结构相同、系数相似。因此,相较于以往的神经网络、支持向量机等数据驱动模型,本文方法具有结构简洁、易于解释的特性。同时,重复上述实验50次,得到的系数均相似,如图5中的箱线图所示,表明了算法的可重复性和可靠性。

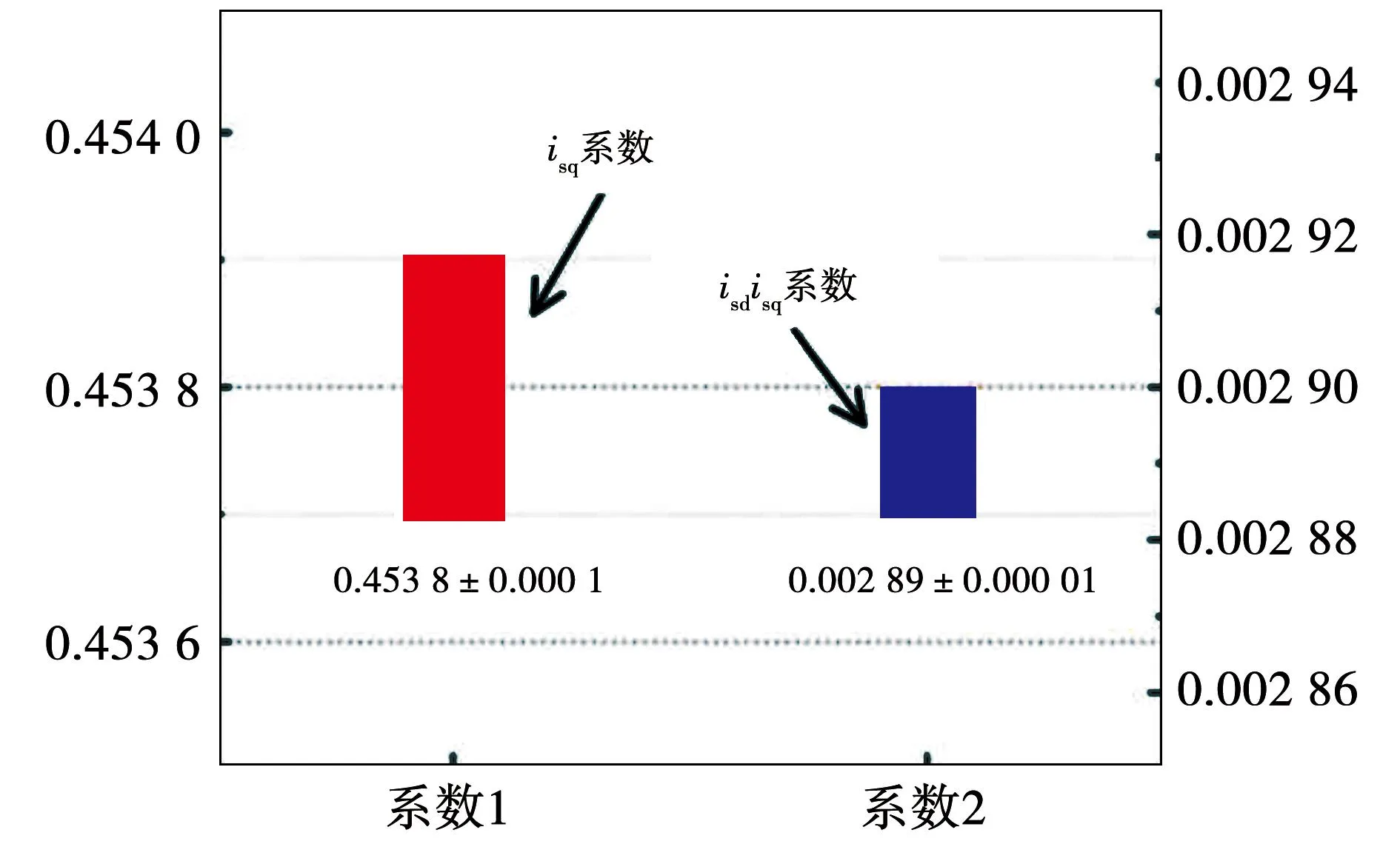
图5 L1正则转矩模型的系数箱型图

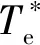
图6 L1正则转矩模型和传统转矩模型的比较

根据式(18)和式(25),可得最终的L1、L2正则表达式为

(26)

再使用2.3节所述方法进行最优λ求解,将式(26)代入式(22),得:

(27)

再结合式(23),经过简化计算,解得最优λ*近似值为

(28)

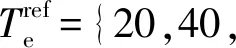
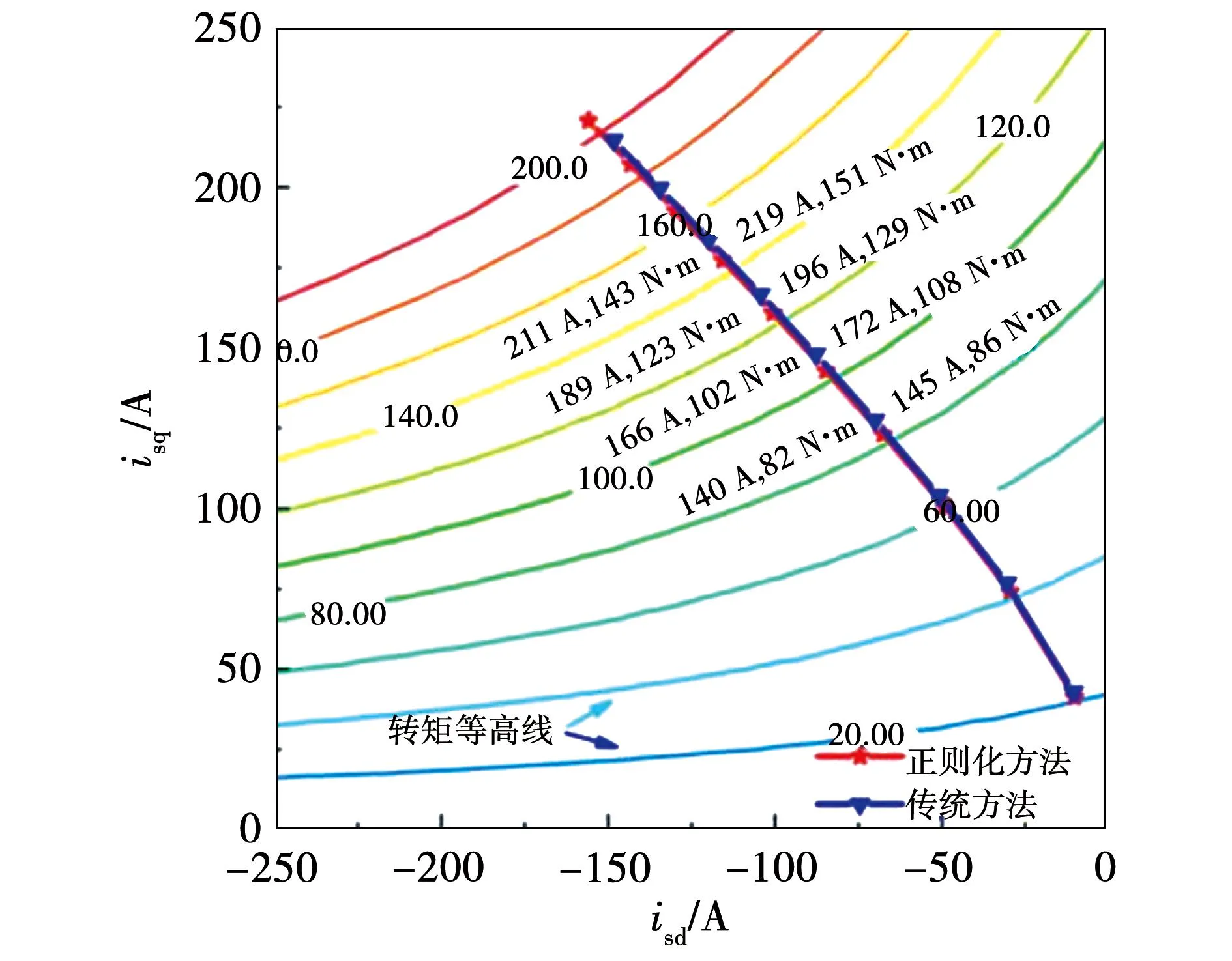
图7 正则化MTPA方法和传统MTPA方法的比较

3.2 变Ld、Lq参数值的MTPA控制策略

考虑磁饱和以及交叉磁饱和的影响,实际中Ld、Lq的值往往会跟随不同isd、isq的值发生变化,在实际中,测得某台电机的Ld、Lq变化如图8所示,根据图8中的isd、isq建立Ld、Lq的查找表。同样在弱磁区以下让电机运行于不同的转速和转矩,并采集转矩数据Te、d轴电流数据isd以及q轴电流数据isq,最后使用式(16)中的L1正则方法进行Te=ΞΘ(is)求解,解得变Ld、Lq参数下的转矩Te模型为

图8 变Ld、Lq条件下的Ld、Lq值分布

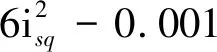
(29)

可以发现,虽然Ld、Lq的变化较为复杂,但基于L1正则方法仍然给出了最简洁的转矩模型。

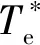
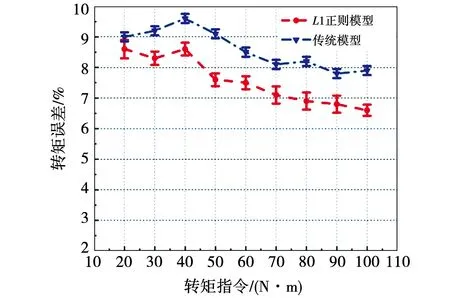
图9 使用L1正则模型和传统模型的转矩比较

根据式(18)和式(29),可得最终的L1、L2正则表达式为

(30)

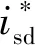
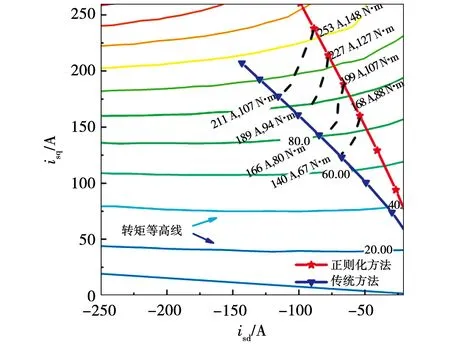
图10 正则化MTPA方法和传统MTPA方法比较

3.3 结果讨论

从3.1节的结果中可以看出,在恒Ld、Lq的工况下,正则化MTPA方法与传统MTPA相比结果相差不大。这是因为在Ld、Lq的精确值已知、且为恒定的条件下,转矩模型较为简单,传统转矩模型和L1正则转矩模型具有相同的结构和相近的系数,同时,在Simulink仿真环境中的电机模型多为理想模型,不用考虑模型误差和外部环境干扰的问题。由此可以得出结论:在模型参数精确值已知且恒定,并且不存在模型误差和外部干扰的条件下,本文研究的正则化MTPA方法相较传统MTPA方法优势并不明显。不过,上述的条件过于理想,在实际工程中并不容易实现。

而从3.2节的结果中可以看出,在Ld、Lq根据不同工况发生变化的条件下,正则化MTPA方法较传统MTPA具有明显优势。这是因为在变Ld、Lq的工况下,使用式(3)已经无法描述精确的转矩模型,从而造成了较大的转矩跟踪误差;而正则化MTPA方法使用实际运行数据来对转矩进行数据建模,从而有效避免了由于电感饱和效应导致的模型误差以及实际运行环境带来的干扰,显著提升了转矩跟踪精度。同时,从式(25)和式(29)可以看出,虽然本文的方法也是数据驱动方法,但是使用L1正则方法可以获得结构简洁、易于解释、利于工程实现的数据模型,这是其他数据驱动方法,例如神经网络、支持向量机等方法不具备的优势。

综上所述,本文研究的正则化MTPA方法适用于存在模型误差和实际环境干扰的运行场合,并且兼顾了精确性、简洁性和可解释性。

4 实验验证

4.1 实验环境与实验步骤

所研究的方法在AVL电机台架上进行试验验证,试验平台如图11所示,由被测电机、被测电机控制器以及测功机构成。实验时,被测电机运行于转矩模式,测功机运行于转速模式。被测内置式永磁同步电机与第3节仿真中的电机参数相同,被测电机控制器的主控芯片为TI公司的TMS320280049型DSP。具体实验步骤如下:

图11 实验平台示意图

1)测功机以300 r/min转速步长分别运行于n={300,600,…,3 000 r/min},被测电机在不同转速n下,以不同的isd、isq电流运行,以便输出不同转矩。

2)在步骤1所述的不同转速、转矩、电流条件下,分别采集被测电机的运行数据,包括转速n、电机转矩Te、d轴电流isd、q轴电流isq,记为{n,Te,isd,isq},共计400组。

3)使用步骤2采集的400组数据进行被测电机转矩的L1正则化建模,L1正则化建模使用式(17)所示的LASSO回归实现,并用MATLAB语言在PC机中完成。所建立的L1正则化转矩模型具有结构简单的特征,可以移植到电机控制器的DSP中。

4.2 实验结果与分析

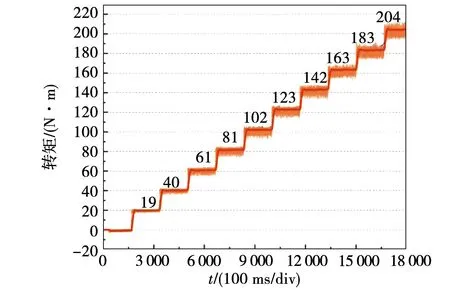
图12 使用本文方法的输出转矩示意图

图13 使用基于模型方法的输出转矩示意图

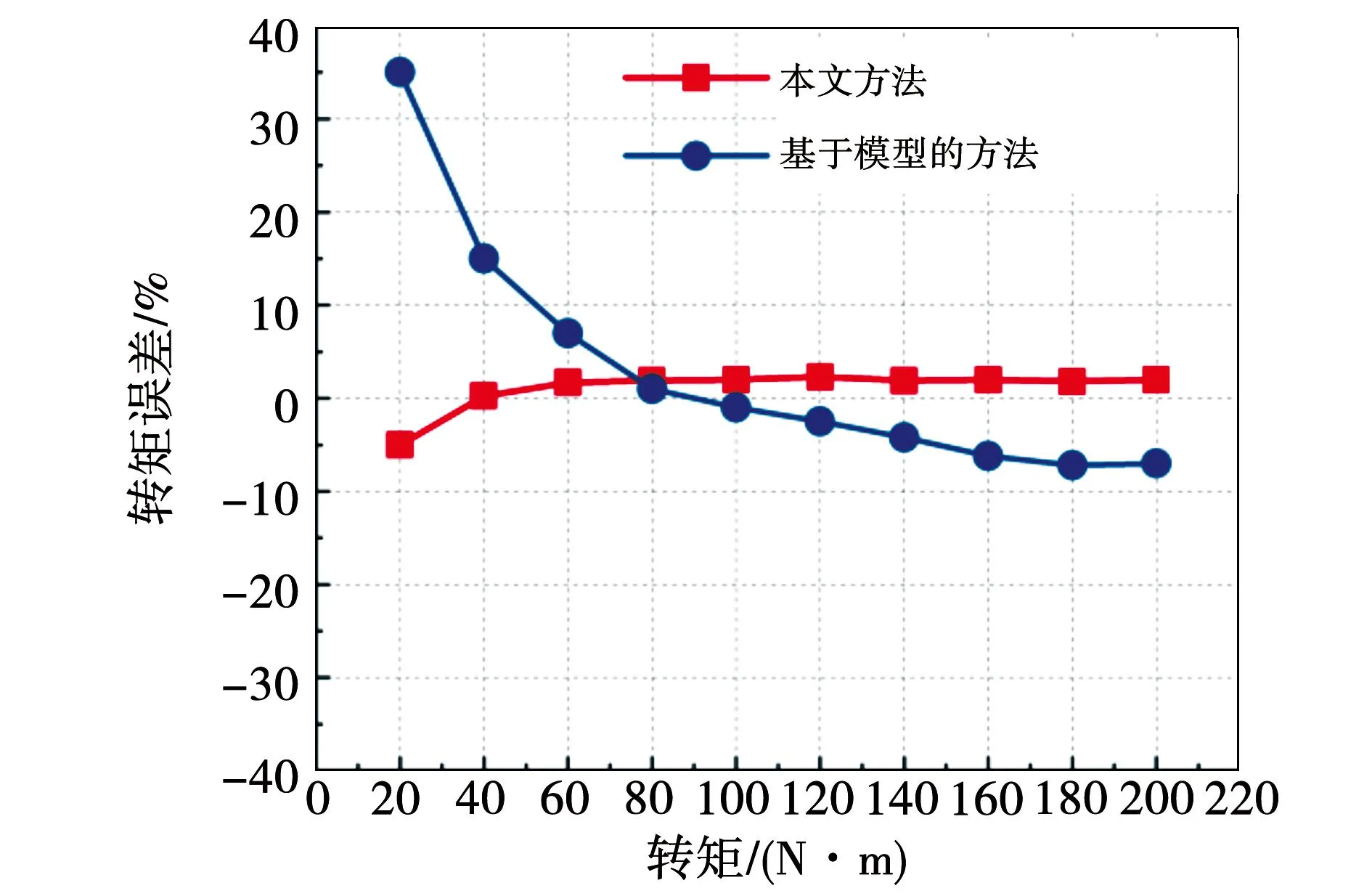
图14 本文方法和基于模型方法转矩跟踪误差

图15为本文方法和基于模型方法的is电流绝对值比较,可以发现,在转矩指令较小时,基于模型方法的is电流绝对值大于本文的正则化MTPA方法,而在转矩指令较大时,基于模型方法的is电流绝对值小于本文的正则化MTPA方法。这是由于图15所示的转矩跟踪误差所导致的。在转矩指令较低时,基于模型的方法会输出远大于指令的转矩,从而需要更高的电流值;而在转矩指令较高时,基于模型的方法会输出远小于指令的转矩,从而需要更低的电流值。而在转矩误差相近的区域,两种方法的电流值相差不大。这表明,基于模型的方法和本文的方法都是以最小电流作为优化指标,因此都可以输出较小的电流值。不过由于转矩误差的不同,两种方法在不同的转矩指令范围内输出的电流值也不尽相同。

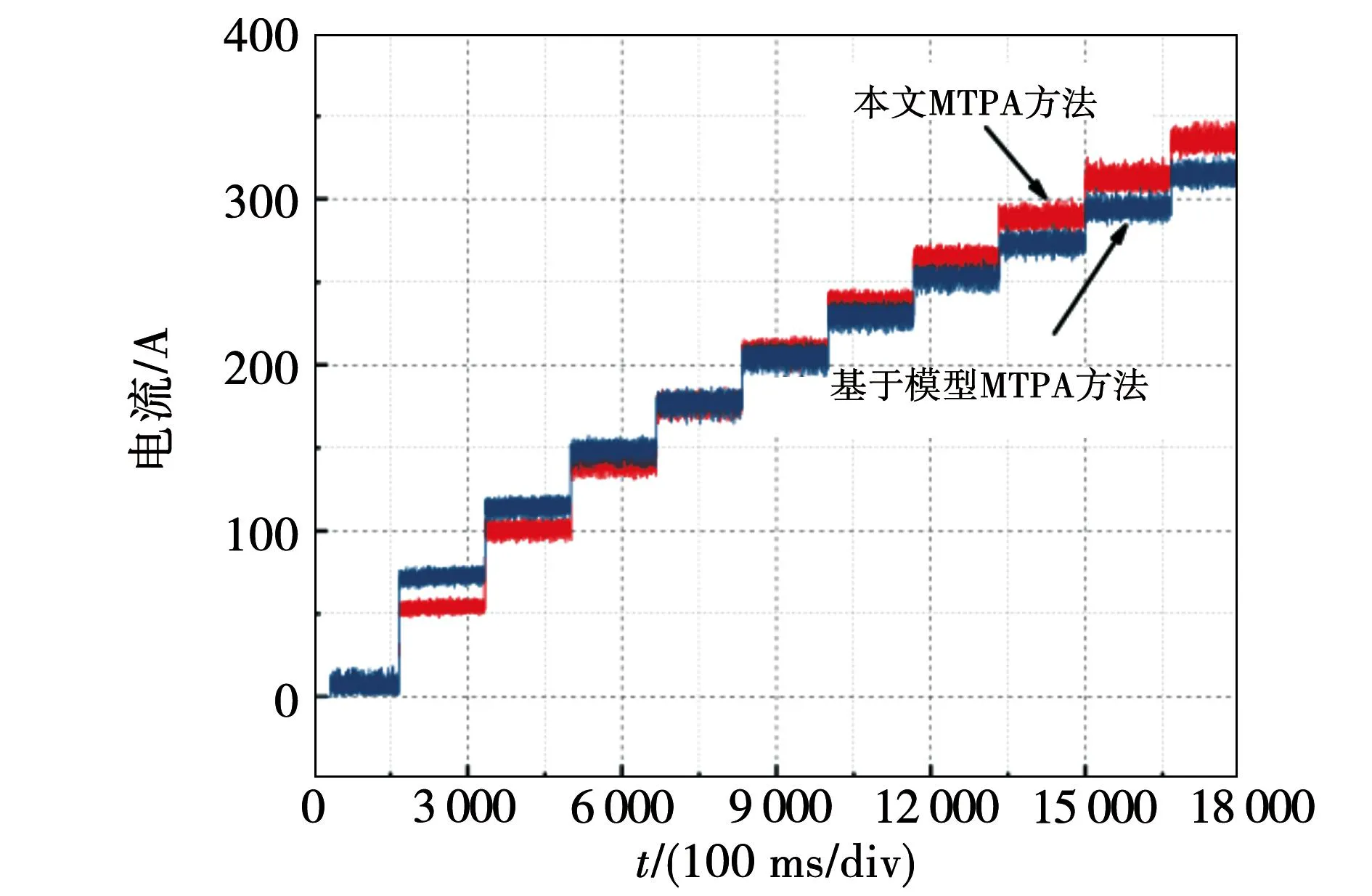
图15 本文方法和基于模型方法的is电流值比较

为验证本文方法在不同转速下的表现以及在转速发生突变时的鲁棒性,设置实验如下:电机初始转速为900 r/min,在电机运行的过程中,转速增至2 400 r/min,然后回调转速至300 r/min。图16为整个运行过程中的电机输出转矩。可以发现,使用本文方法,在不同转速均能使电机稳定、精确地运行。同时,在转速突变时,所述方法也能够进行快速地转矩调节,表明了算法的鲁棒性。

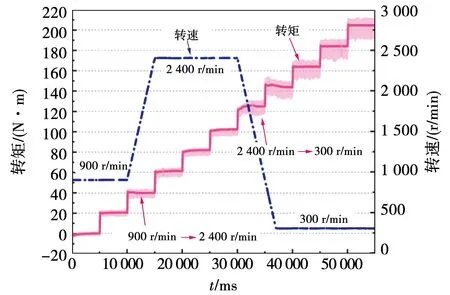
图16 使用本文方法在不同转速下的转矩输出

5 结 论

本文借鉴了机器学习中的正则化理论,提出一种基于L1和L2正则的内置式永磁同步电机转矩跟踪型MTPA方法。研究表明,将内置式永磁同步电机的MTPA控制问题转化为机器学习中的正则化问题进行求解后,其电流计算结果不仅具有传统的最优转矩电流比特性,还具有精确跟踪转矩指令的特性。仿真和实验结果表明,本文研究的方法适用于存在模型误差和实验环境干扰的场合,可以有效地避免由于模型误差和电感交叉饱和特性而造成的性能降低,保证了指令转矩跟踪的精确性。同时,本文的方法既可以得到兼顾最大转矩电流比和高转矩跟踪精度的最优解,又针对MTPA问题可以获得结构简单、易于解释的解析解,从而融合了模型驱动和数据驱动MTPA方法的优势。