新型不对称多电平逆变器拓扑及其调制策略

胡文华, 熊志磊, 余书琨, 丁文斌, 张建辉

(华东交通大学 电气与自动化工程学院,江西 南昌 330013)

0 引 言

近些年,在电力电子行业领域中,多电平逆变器发挥着越来越重要的作用[1-3]。与传统的两电平逆变器相比,多电平逆变具有输出电压电平数量多、输出谐波含量少、开关器件电压应力小、开关损耗低等优点[4-7]。因此,在新能源发电系统中多电平逆变器得到广泛的应用,尤其是在光伏、风力等新能源的开发和利用上具有广阔的应用前景[8-9]。

多电平逆变器被广泛使用的类型包括有以下3种:二极管箝位型[10]、飞跨电容型[11]和级联H桥型[12]。其中,二极管箝位型逆变器想要输出高质量的多电平电压则需要大量的箝位二极管,且这种多电平逆变器设计比较复杂,电路中电容间的电压极易分布不均匀。飞跨电容型逆变器也存在电容间的电压分布不均匀的问题,而且需要的电容数量较多,增加成本的同时也会使电路在电容均压技术方面增大难度。级联H桥逆变器的电路简单,由每个独立的电源为其电路供电,所以不存在电容纹波以及电容电压不均匀的问题,但是级联H桥输出多电平电压时需要大量的电源,这会增加电路消耗成本和开关损耗。文献[13]在传统级联H桥逆变器的基础上提出了一种混合级联H桥逆变器,其优势在于输出同样的电平数的情况下可减少级联单元数从而减少了电源数量,但是这种的多电平逆变器还是需要大量的开关单元进行级联。文献[14]提出一种改进的对称多电平逆变器电路,虽然减少了开关管数量输出多电平,但是使用的电压数量较多,总电压应力较大。文献[15]提出的一种开关电容多电平逆变器,减少了独立直流电源数量,但其使用的开关器件数量比较多。文献[16]提出一种基于H桥的电容型多电平逆变器,通过H桥来控制输出电平的正负。文献[17]为了减少独立电源的数量,提出一种T型开关电容多电平逆变器,该逆变器需要扩展进行多电平的输出,扩展需要增加电容和大量的开关管。

从现在有文献中可以看出,在提高输出电平数量的同时减少使用直流电源、储能元件以及开关管数量方面仍然需要进行大量的改进工作。本文在减少电源数量以及开关管数量的基础上提出一种新的拓扑逆变器,拓扑结构独立于储能元件,不存在均衡充电问题和电容纹波损耗。保证输出电平的质量,电平数越高输出的波形质量越好,输出负载电压波形畸变率(total harmonics distortion,THD)就越低。本文所提的拓扑可以在较低的工作频率下工作,因此,系统的传导损耗以及总损耗显著降低,从而提高整个系统的工作效率。另外,所提拓扑需要的开关管器件数量较少,与现有的拓扑对比,不仅在提高效率的同时,将大大降低成本。

1 多电平逆变器的拓扑结构与原理

1.1 逆变器各单元输出功率分析

上述提出的多电平逆变器的电路结构如图1所示。由10个带有反并联二极管的功率开关器件、5个功率二极管和3个独立直流电压源组成。通过合理设计将3个不对称直流电压源在不同开关组合的条件下,叠加输出得到我们所需的多电平。

图1 新型多电平逆变器拓扑

图1的左半部分的6个开关管(S1～S6)逻辑组合构成多电平发生器,通过控制这6个开关管的通断,可以得到0、E1、E2、E3、E1+E2、E1+E3、E2+E3、E1+E2+E3等多种电平,可以产生正向半波电流,这个模块再与H桥逆变电路相连,此时仅需4个开关管,就可以将半个周期的电压逆变成负电压,正半周期加上负周期,实现输出完整周期的多电平电压。

该电路结构可以使用的对称的独立电源进行供电如电源电压比为1∶1∶1;也可以使用不对称的独立电源像电压比为1∶1∶2、1∶2∶3、1∶2∶4等等。其优势在于灵活运用于低功率可再生能源应用中,用最少的开关器件实现最大的电平输出。为了解决不对称独立电源的隔离问题,以电源电压比1∶2∶4为例,采用蓄电池串联进行供电,独立电源E2和E3分别串联2个和4个与E1型号相同的蓄电池进行供电。该拓扑能最大输出的是十五电平,使用H桥作为逆变器,多电平发生器只会产生零电平和正电平,所以整个电路中不会产生电流倒灌的现象,这也使得总损耗降低,从而提高了系统的整体效率。

1.2 逆变器工作原理分析

以输出十五电平为例,电压比为E1∶E2∶E3=1∶2∶4介绍该型逆变器的工作原理。前面提到了图1左半部分的6个开关管逻辑组合为该拓扑的多电平发生器,在这一部分中能产生0、E、2E、3E、4E、5E、6E、7E等多种电平,每产生一种电平对应一种工作模态,如图2所示,7个不同的工作模态清晰地介绍了7种电平(0除外)的产生。负周期的电平是通过H桥的进行逆变得到的,因此,介绍以下7种模态足以理解整个逆变器电路的工作原理。表1展现了该逆变器输出多电平电压时各个开关管的通断状态,其中1和0分别代表逆变器中开关管的导通和关断状态。

表1 各种电平下开关管的状态

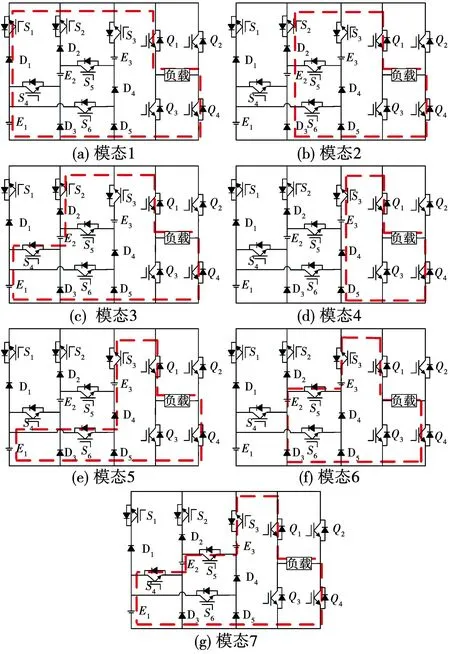
图2 逆变器的工作模态

模态1,如图2(a)所示,单元中开关S1导通,其他开关管关闭,电流如图所示流经整个电路,此时二极管D1承受的是正向电压,D1导通,电源E1单独进行放电,电路输出的电压为E。

模态2,如图2(b)所示,单元中开关管S2导通,其他开关管关闭,电流如图所示流经整个电路,此时D2和D3承受的均为正向电压,D2、D3导通,电源E2单独进行放电,电路输出的电压为2E。

模态3,如图2(c)所示,单元中开关管S2和S6导通,其他开关管关闭,电流如图所示流经整个电路,此时D2承受的为正向电压,D2导通,电源E1和E2同时进行放电,电路输出的电压为3E。

模态4,如图2(d)所示,单元中开关管S3导通,其他开关关闭,电流如图所示流经整个电路,此时D5承受的是正向电压,D5导通,电源E3单独进行放电,电路输出的电压为4E。

模态5,如图2(e)所示,单元中开关管S3和S4导通,其他开关管关闭,电流如图所示流经整个电路,此时D4承受的是正向电压,D4导通,电源E1和E3同时对负载进行放电,电路输出的电压为5E。

模态6,如图2(f)所示,单元中开关管S3和S5导通,其他开关管关闭,电流如图所示流经整个电路,此时D3承受正向电压,D3导通,电源E2和E3同时对负载进行放电,电路输出的电压为6E。

模态7,如图2(g)所示,单元中开关管S3、S5和S6导通,其他开关管断开,电流如图所示流经整个电路,此时D3和D5承受反向电压,二极管截止,电源E1、E2、E3同时对负载进行放电,电路输出的电压为7E。

2 调制策略分析与拓扑对比

2.1 逆变器调制策略分析

本文采用一种新型改进的载波移幅调制策略,在同相载波层叠调制的基础上进行改进,大大减少载波的数量,传统的载波移幅调制需要14个载波进行调制,本文则缩减至7个载波,方法是把正弦波绝对值化得到调制波vm,再将正半轴的7个同相三角载波信号vcr1～vcr7分别和该调制波vm进行比较得到不同的脉冲信号,再根据各个开关管的逻辑导通顺序进行逻辑组合得到开关信号。

调制波的频率为f,幅值为Am,7个载波的频率为fcr,幅值为Acr,如图3所示,由于幅值和频率已知,因此调制波的表达式为

图3 改进的载波移幅调制原理

f(t)=Am|sin(2πft)|。

(1)

调制比为

(2)

载波比为

(3)

在调制周期内,根据所提的新型多电平逆变器的各种原理及各开关管状态分析可以推出,在输出区间[0,E]内,当vcr1vcr7,得到脉冲信号A7,同时开关管S3和S5和S6导通。其中H桥的4个开关管对应的脉冲信号如图Q1,4和Q2,3所示。最后通过逻辑运算得到调制周期时各开关管的驱动逻辑信号为:

(4)

开关管S1～S6以及H桥4个开关管Q1～Q4的通断状态如图4所示。

图4 开关管通断状态

2.2 逆变器损耗分析

多电平逆变器的功率损耗主要来自于开关损耗和通态损耗。其中开关损耗是指在开关通断状态下特定的过渡时间下电压和电流发生重叠时产生的损耗,在过渡时,电压和电流同时变化,而这个过渡时间可以定义为开关打开和关断(ton和toff),所以开关损耗可以分为导通损耗Pon和关闭损耗Poff,计算公式如下:

(5)

(6)

式中:fs为开关频率;Uon,k和Uoff,k为第k个开关管导通或者关断时的压降;Ion,k和Ioff,k为第k个开关管完全接通和断开之前的电流。

结合式(5)和式(6)可得在一个周期T内产生的总开关损耗为

(7)

通态损耗主要是开关管和二极管产生的,因此器件的通态损耗Qc可以表示为:

(8)

(9)

结合式(8)和式(9)可得在一个周期T内产生的通态损耗为

Qc=Qc,sw+Qc,d。

(10)

式中Isw,avg和Isw,rms分别表示的是通过开关管的平均电流和均方根电流,而Id,avg和Id,rms分别表示的是通过二极管的平均电流和均方根电流。根据式(7)和式(10)可以计算出电路的开关损耗和通态损耗,求和得到电路的总损耗Ploss为

Ploss=Psw+Qc。

(11)

多电平逆变器的效率计算为

(12)

2.3 逆变器拓扑对比分析

为了比较出逆变器的性能优劣,本文所提的拓扑将与最新提出的几种优秀的十五电平逆变器进行比较,对比每个拓扑需要的电源数,开关器件数量,电容数量,二极管数量以及开关管电压总应力(total standing voltage,TSV)。对比结果如表2所示。

表2 逆变器拓扑与其他逆变器拓扑比较

从表中可以看出,本文提的逆变器在使用器件数量上是有一定优势的,用最少的开关器件输出最多的电平数。相比文献[17],虽然他仅需一个电源供电,但是需要使用多个电容代替电源对负载进行供电,而且通过电容供电需要考虑电容之间电压均衡的问题和电容纹波的问题。在输出相同电平数的情况下,本文所提拓扑在开关器件以及电容数量等方面具有一定的优势,电压总应力也比文献[17]低3E;对比文献[14],同样使用H桥作为逆变电路进行负周期的电平转换输出,本文拓扑的优势在于,输出同样的电平数下,所需要的电源数少4个,开关管的数量少2个,电压总应力低2E,总体比文献[14]所提的拓扑更具有实用性和经济性。文献[13]所提的是传统的混合级联H桥逆变器的拓扑,此类拓扑最近几年也非常热门,相比此类逆变器,本文所提的拓扑优势在于使用较少的开关器件输出较多的电平数量,所需的电源模块少,开关管的电压总应力比混合逆变器小得多。

3 仿真研究

为了验证本文所提逆变器拓扑及其调制策略的正确性,用MATLAB/Simulink仿真工具搭建逆变器仿真模型进行仿真分析。仿真电路参数设置如表3所示。

表3 仿真参数

图5为本文所提新拓扑在改进的载波移幅调制策略下在不同调制度时输出的电压电流的仿真波形。此次仿真是在阻感性负载的条件下进行仿真,得到的输出电压波形为阶梯状的正弦波,而输出电流波形则为平滑的正弦波。在调制度为0.9和0.6以及0.3的条件下,仿真得到阶梯状的输出电压分别从十五电平变为十一电平再至七电平,而输出电流波形则一直为平滑的正弦波。

图5 不同调制下输出电压电流的波形

图6为本文所提逆变器在改进的载波移幅调制策略下不同的调制度时所输出的相电压频谱分析图。从图6可以看出输出相电压的谐波含量主要集中在4 kHz及其附近。随着调制度的降低,输出相电压的基波幅值也随之降低,相应的THD值则随之增大。根据分析本文的调制策略保留了传统载波移幅调制策略控制简单、易于实现,尤其是能显著降低输出电压的THD值的优点。在显著降低THD值的同时,比传统载波移幅调制所需载波的一半数量进行调制实现多电平的输出。这在多电平逆变器的应用上,尤其是在超过九电平逆变器的载波移幅调制策略调制上,载波数量大幅度减少,控制方法的难度也相应的降低,使得控制起来更加方便。

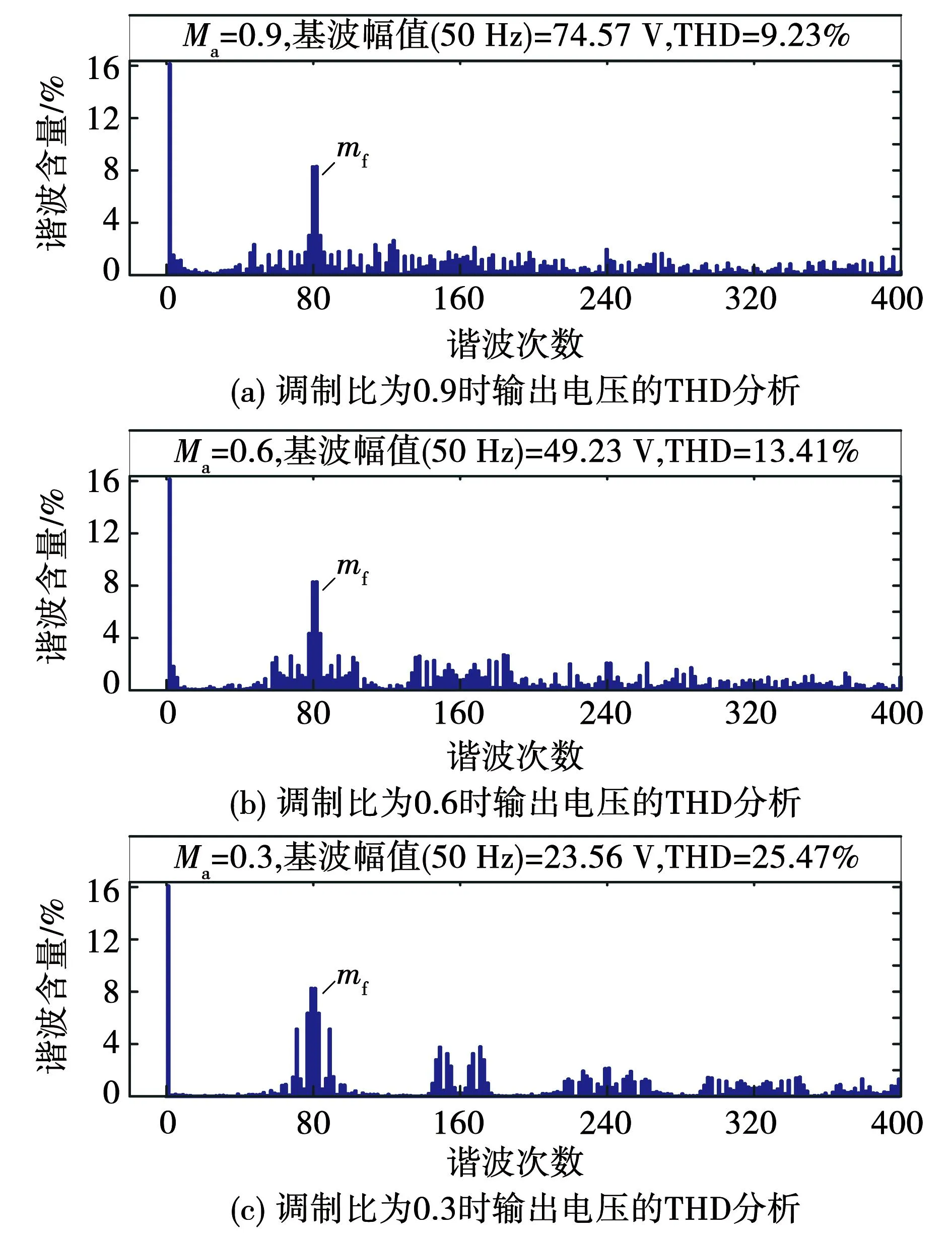
图6 改进载波移幅调制下逆变器输出相电压频谱

4 实验结果分析

为进一步验证所提逆变器拓扑及其调制策略的正确性以及其动态性能,搭建了一套本文所提新拓扑逆变器的实验样机,在输入直流电压幅值为1∶2∶4的前提条件下实现了十五电平的电压输出。本次实验的参数如表4所示。

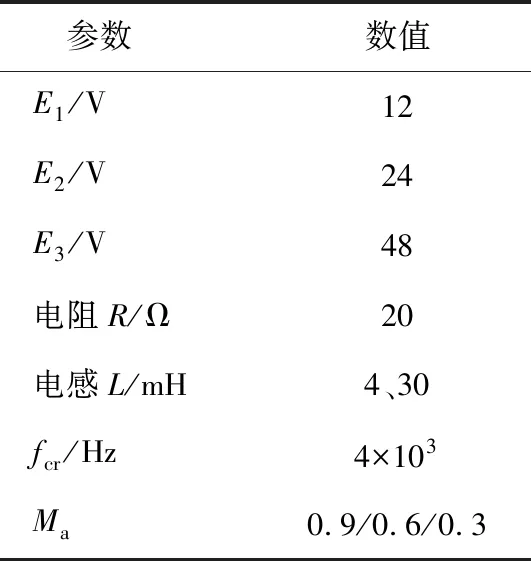
表4 实验参数

4.1 稳态实验结果分析

在调制度为0.9,输入电压为12 V/24 V/48 V,负载为阻感20 Ω、4 mH、30 mH的条件下,得到输出电压和相应的输出电流波形,如图7所示。如图7(b)所示,逆变器输出的电压波形为理想的十五电平波形,得到的输出电压最高电平约为84 V,实现电压增益约1.75倍,同时得到了输出电流峰值约为8 A的一根较为平滑的正弦波。

图7 稳态实验分析波形

稳态实验条件下分析得到逆变器负载为纯阻性时,输出的电流是阶梯波,和输出的电压波形保持一致;逆变器负载为阻感性时,输出的电压波形为十五电平的正弦波,由于电感的滤波作用,输出的电流则是平滑的正弦波,如图7(c)所示。在空载条件得到的输出电压波形如图7(d)所示,输出电压波形依旧为十五电平正弦波,同时无电流输出。

4.2 稳态实验结果分析

为了检验所提逆变器的动态稳定性,在调制比变化、调制波频率变化、负载变化的条件下,对逆变器的动态性能进行实验分析。图8为调制比从0.9变化至0.6再由0.6变化至0.3的输出电压和输出电流波形。在全调制比的范围下,逆变器能正常的工作,而且变化同时响应速度也特别快。

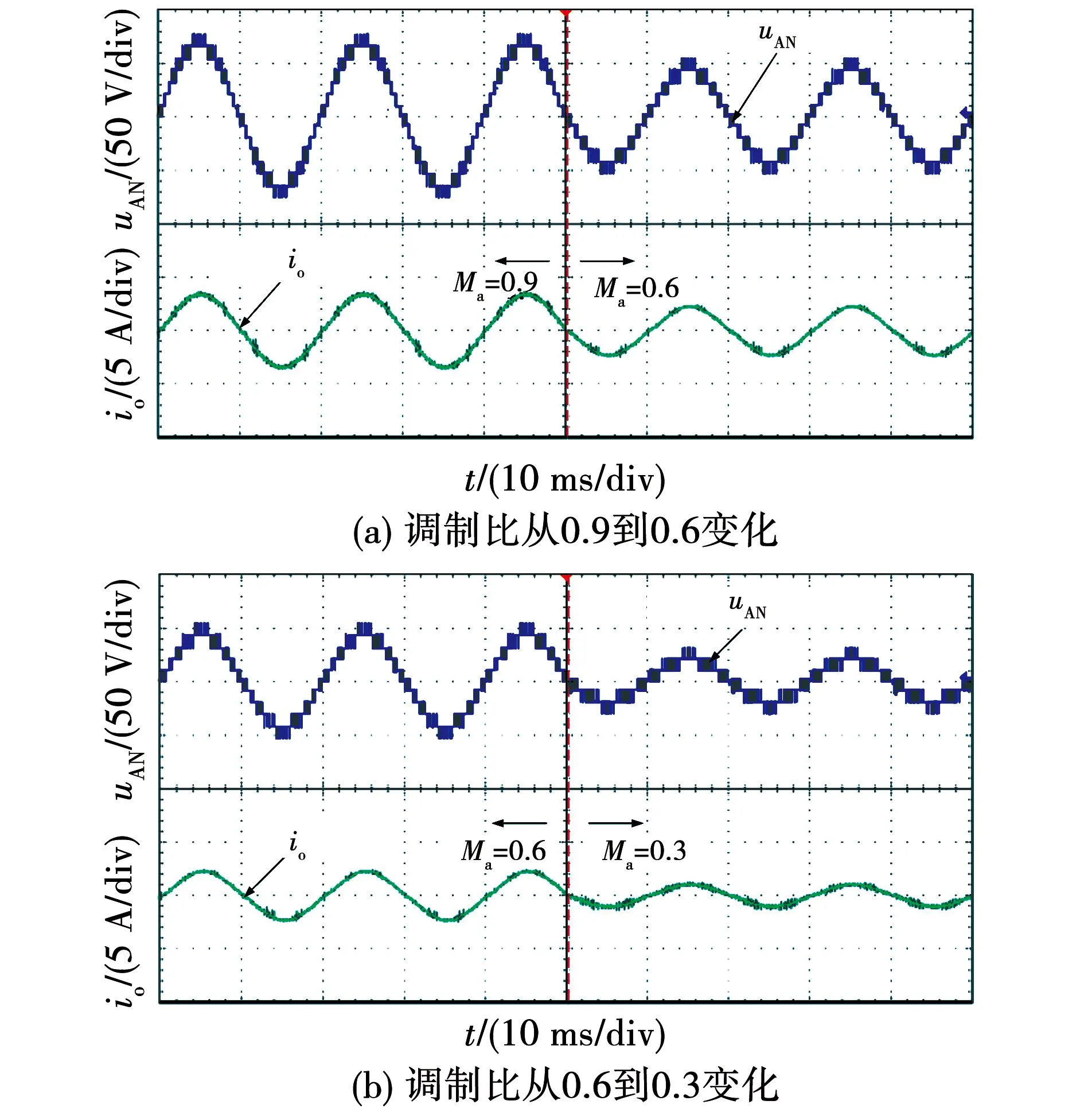
图8 阻感性负载输出电压和电流波形

图9为载波频率改变时所提逆变器输出的电压和电流波形。为了反映逆变器在载波频率发生变化时逆变器的稳定性,在逆变器工作时将频率由50 Hz变化成100 Hz,再由100 Hz换成50 Hz。从中可以得到,逆变器工作时的频率发生变化时,还能正常的工作,并且响应速度也非常快。

改变负载时输出电压和电流的波形如图10所示,分别是纯阻性负载变化至阻感性负载和阻感性负载变化至纯阻性负载这2个动态过程。这2个变化过程中,输出的十五电平电压波形没变化;而输出的电流波形则是由光滑的正弦波变化成输出电压的那种阶梯波和阶梯波变化成光滑的正弦波,响应的速度很快。因此,逆变器可以在负载功率因数发生变化的情况下继续工作。

图10 负载变化时输出电压电流波形

5 结 论

1)本文提出了一种新型的多电平逆变器,该逆变器设计使用了3个不对称的直流电源,在输入直流电压幅值为1∶2∶4的前提下实现了十五电平输出。

2)该拓扑结构独立于储能元件,因此不存在均衡充电问题和电容纹波损耗问题。本文对比了近些年优秀的逆变器拓扑,在输出相同的电平数且开关管电压总应力在可以接受范围内的情况下,该拓扑使用开关器件的数量较少,具有一定的优势。

3)应用改进的载波移幅调制策略对本文所提的拓扑进行调制输出十五电平,比传统的载波移幅调制减少一半的载波数量,使得控制简单,降低了成本并保留了载波移幅调制谐波含量低的优点。

4)对本文所提拓扑结构及其调制策略进行了仿真分析和实验验证,实验结果表明了该拓扑结构及其调制策略的正确性、可行性和优良的动态性能。