非理想电网电压下MMC-UPQC的PBC-SMC控制策略研究

朱纯, 龚波涛, 程启明, 蒋谦, 王晓锋, 黄志豪

(1.国网上海市电力公司,上海 200122; 2.上海电力大学 自动化工程学院,上海 200090)

0 引 言

由于大电压、高功率且可共用的直流侧,模块化多电平换流器(modular multi-level converter,MMC)[1]适于高压直流输电和其他电气领域[2-3]。MMC已用在有源电力滤波器上,它能够抑制电流谐波,它和统一电能质量控制器(unified power quality controller,UPQC)组合而成的MMC-UPQC可以抑制电压与电流谐波[4-5]。MMC-UPQC由并联变换器和串联变换器组成,两个变换器之间协调控制能够同时抑制电流与电压的谐波,提高电能质量,维持电网可靠安全。但当非理想电网电压时,电能质量更难得到保障,此时电流与电压的补偿控制策略成为核心关键因素。

近年来,人们尝试对MMC-UPQC采用了多种不同的补偿控制策略。文献[6-7]采用线性PID控制,对于非线性的MMC-UPQC对象,PID控制效果并不令人满意;文献[8]采用了模糊PID控制,但由于无环流抑制和均压控制,可能会使输出难以稳定;文献[9-10]采用了改进PID控制,尽管系统成本较低,但增加了计算量且控制变得复杂;文献[11-12]仅分析了MMC-UPQC并联侧电流补偿策略,没有分析串联侧电压补偿策略;文献[13]采用PID控制且加上限流措施,分析了串联侧变换器的补偿电压方法,但对并联侧变换器的补偿电流效果一般;文献[14]采用了滞环控制用于变换器控制补偿上,但控制精确度不高、超调较高;文献[15]提出了理想的电网电压下串并联两个变换器的协调控制方法,但补偿效果有待提高;文献[16]设计了不平衡电压条件下正负序相等的控制策略,但串联与并联两个变换器不能同时组合和投入。

由于MMC-UPQC具有非线性特征,应该选用非线性控制策略才能达到很好的控制效果。非线性的无源性控制(passivity-based control,PBC)具有全局稳定性,且物理清晰、结构简单、参数少和响应快,它用能量观点和加入阻尼角度分析系统的稳定性,现已在电气对象控制上得到良好应用[17-19]。但它依赖于对象模型精确度,目前MMC-UPQC的PBC控制方法中控制参数不变,若MMC-UPQC内部参数变化或外部负载变化时,控制性能明显下降,导致MMC-UPQC的精确度低、响应慢,且电能质量的补偿不佳。

非线性的滑模控制(sliding-mode control,SMC)具有对内外变化不敏感,且响应快速、原理简单、实现容易等特点,能够快速适应对象的内部参数变化和外部环境扰动,其鲁棒性和抗扰性很强[20-21],但其会在稳定点上下两侧穿越靠近平衡点,从而产生高频抖振问题。因此,SMC控制用在MMC-UPQC上的电压质量补偿也不佳。

总之,PBC控制和SMC控制各有其特点,且两者优点互补,若把他们两者结合在一起,可弥补其各自的不足,从而提出PBC和SMC组合的PBC-SMC控制方法,使其同时具有PBC控制的响应速度快和全局稳态性等特点,也兼具滑模控制的抗扰性和鲁棒性强等优点。本文首次创新性地在非理想电网电压下将PBC-SMC控制策略用到MMC-UPQC电能质量补偿上。首先,按照无源性控制理论,推出MMC-UPQC的欧拉-拉格朗日(Euler-Lagrange,EL)无源性数学模型,并判别系统是否具有无源特性,进而再设计PBC控制;接着,针对PBC控制存在的问题,提出无源性滑模控制策略,并推导出非理想电网电压下MMC-UPQC串联变换器和并联变换器的PBC-SMC控制策略的控制律。最后,通过MATLAB/Simulink软件仿真,并把PBC-SMC控制与单一的PID、PBC进行对比分析,验证所提的PBC-SMC方法具有抗扰性强、响应快、精确度高和补偿好等特点。

1 MMC-UPQC的拓扑结构和数学模型

1.1 MMC-UPQC电路拓扑

MMC-UPQC系统的拓扑结构如图1所示。由图可见,MMC-UPQC系统的串联变换器和并联变换器均用MMC结构,且两个MMC通过中间直流环节的大电容采用背对背型式连接在一起。

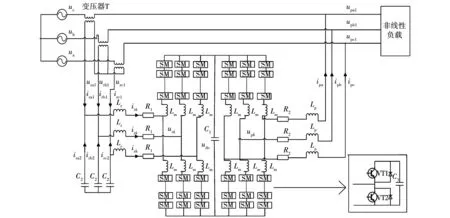
图1 MMC-UPQC电路的拓扑

图中:uk(k=a、b、c)为电网三相电压;upk、urk和ipk、irk分别为MMC-UPQC并联侧(p)、串联侧(r)变换器线路的电压和电流;upk1、urk1分别为MMC-UPQC并联侧的负载线路上电压、串联侧变压器的原边电压;ipk1、irk1为并联侧、串联侧线路上电流;irk2为串联侧电容C2上电流;Lp、Lr为并联侧、串联侧两边连接外部的电感;C1为串联变换器与并联变换器中间的连接电容;R1、R2为串联侧、并联侧的两侧连接的外部电阻。并串两个MMC上下桥臂每一相均包括N个子模块(sub module,SM)和电感Lm,SM包含半桥型电路和电容C3。SM有切(除)、投(入)和闭(锁)共3种运行模式。

1.2 MMC-UPQC的数学模型

由图1的MMC-UPQC电路的拓扑和基尔霍夫定律可得串联侧MMC关系为

(1)

式中:Lreq为串联侧等效电感;Lreq=Lr+Lm/2。

串联端有串接的变压器T,若变压器的变比为m时,存在关系urk1=murk2。类似地可推出并联端MMC关系为

(2)

式中:Lpeq为并联侧等效电感;Lpeq=Lp+Lm/2。

上面的式(1)、式(2)由abc变为dq坐标系下可推出UPQC两侧的数学关系为:

(3)

(4)

式中:下标p、r代表并联侧、串联侧;ω为电网角频率。

2 MMC-UPQC电能质量的补偿原理

MMC-UPQC抑制谐波的原理为:在电网电压不平衡条件下,需要先对电气量做正负序分离,再将无源性滑模控制策略用于电流内环控制上,从而使控制器输出能够适应系统内外部变化的自适应信号。当电网电压质量降低时,串联变换器输出的补偿信号由变压器接到左侧电路上,对电网电压进行补偿,从而维持了电网电压稳定;由并联变换器生成电流补偿信号,并将其并入到线路上,抵除非线性负载引起的电流谐波,以免电流谐波加到电网上,从而使MMC-UPQC电压、电流质量均能得到治理。

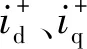
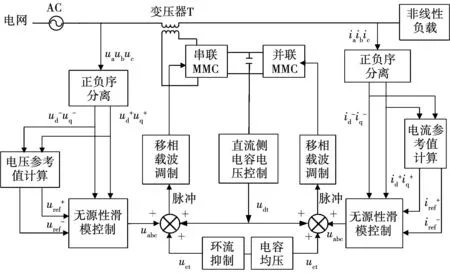
图2 MMC-UPQC的PBC-SMC控制系统框图

3 MMC-UPQC的PBC-SMC控制策略

下面先简介PBC和SMC,再把他们两者组合为PBC-SMC控制策略。

3.1 MMC-UPQC的PBC控制

非线性PBC的原理为系统能量的增量不能大于外部注入的能量,它根据系统的电路结构推出EL数学模型,并使闭环系统具有无源特征,再注入阻尼使系统控制达到预期结果。PBC控制具有控制思路明了、控制系统简单、算法参数少、控制响应快和抗扰性较强优点。

3.1.1 PBC的EL数学模型构建

将式(3)的串联部分和式(4)的并联部分用同一个表达式表示,可得出MMC-UPQC两端输出端数学关系为:

(5)

式中:usd1、usq1为连接MMC-UPQC两侧线路上的三相电压转化为d、q坐标系下的电压;usd、usq为两侧MMC输出电压在d、q坐标系下电压;Rz、L为线路电阻、等效电感;id、iq为d、q轴上线路流过的电流。

PBC控制的EL模型的型式为

(6)

其中:

式中:x、u为状态向量、输入向量;J、R和M为耗散矩阵(半正定)、互联矩阵(反对称)和储能矩阵(正定)。

3.1.2 系统的无源性和稳定性证明

对于下面某系统:

(7)

式中:x、u和y为系统的状态变量、输入变量和输出变量;f(·)、h(·)为Lipschitz函数、某个连续函数。

若式(7)系统存在半正定的储能函数H(x)和正定函数Q(x),且下面的关系式(8)或式(9)成立。

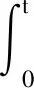
(8)

或

(9)

则这样的系统具有严格的无源特性[17-18],该系统可采用PBC控制且控制系统一定渐近大范围稳定[19-20]。

从式(6)可知

(10)

3.1.3 不平衡电网电压下MMC-UPQC的PBC控制器设计

dq坐标系上MMC-UPQC正序与负序的平衡点为

(11)

系统状态变量的误差如下:

(12)

将式(12)代入式(6)中可得到关系:

(13)

正、负两序系统的储能误差函数可选为

(14)

上面的储能误差函数能够收敛于0,且平衡点也收敛于0,这代表了MMC-UPQC具有严格的无源特性。由于系统的收敛速度不高,通过另外加入一定量的阻尼值,可以使收敛加快、抖振降低、动态特性增强。

本文的MMC-UPQC系统另外注入的阻尼为:

(15)

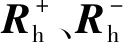
(16)

由此式(13)改写为:

(17)

从而可推出不平衡电网电压下MMC-UPQC正序、负序的PBC控制律为:

(18)

(19)

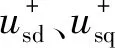
3.2 MMC-UPQC的PBC-SMC控制策略设计

PBC控制与系统数学模型直接相关,且式(18)和式(19)的PBC控制律的中控制参数取固定值,当MMC-UPQC的内部模型参数改变或者外部负荷性变化时,由于PBC的控制参数不能自适应修正,也即控制系统抗性扰性差从而引起系统的响应变慢、精确度变低、谐波补偿质量差。SMC不依赖于系统数学模型,它的抗扰性高、鲁棒性强且响应也快[21-22]。因此,本文把PBC与SMC两者联合起来提出了不平衡电网电压下MMC-UPQC的PBC-SMC控制策略。采用PBC-SMC控制后,既克服了无源控制易受内外和外部变化影响而导致系统稳定性变差,也增加了系统具有响应加快、鲁棒性变强等优点。

在EL模型的PBC控制基础上加入SMC。

首先滑模面s1、s2选择为:

(20)

由式(5)可推出:

(21)

(22)

SMC控制最大问题是高频抖振较大,为此可通过选用sgn(s1)、sgn(s2)符号函数降低抖振。这样SMC的趋近率可取为:

(23)

其中:

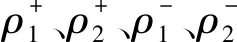
为此可把式(23)中sgn(·)符号函数改为sat(·)饱和函数,这样可更大减小SMC的抖振。这样趋近率修改为:

(24)

由此可以得出结论:

(25)

根据上面公式可得关系:

(26)

因此,不平衡电网电压下MMC-UPQC正序、负序的PBC-SMC控制的控制律为:

(27)

(28)

3.3 PBC-SMC控制策略的参数选取

3.3.1 PBC控制的注入阻尼值选取

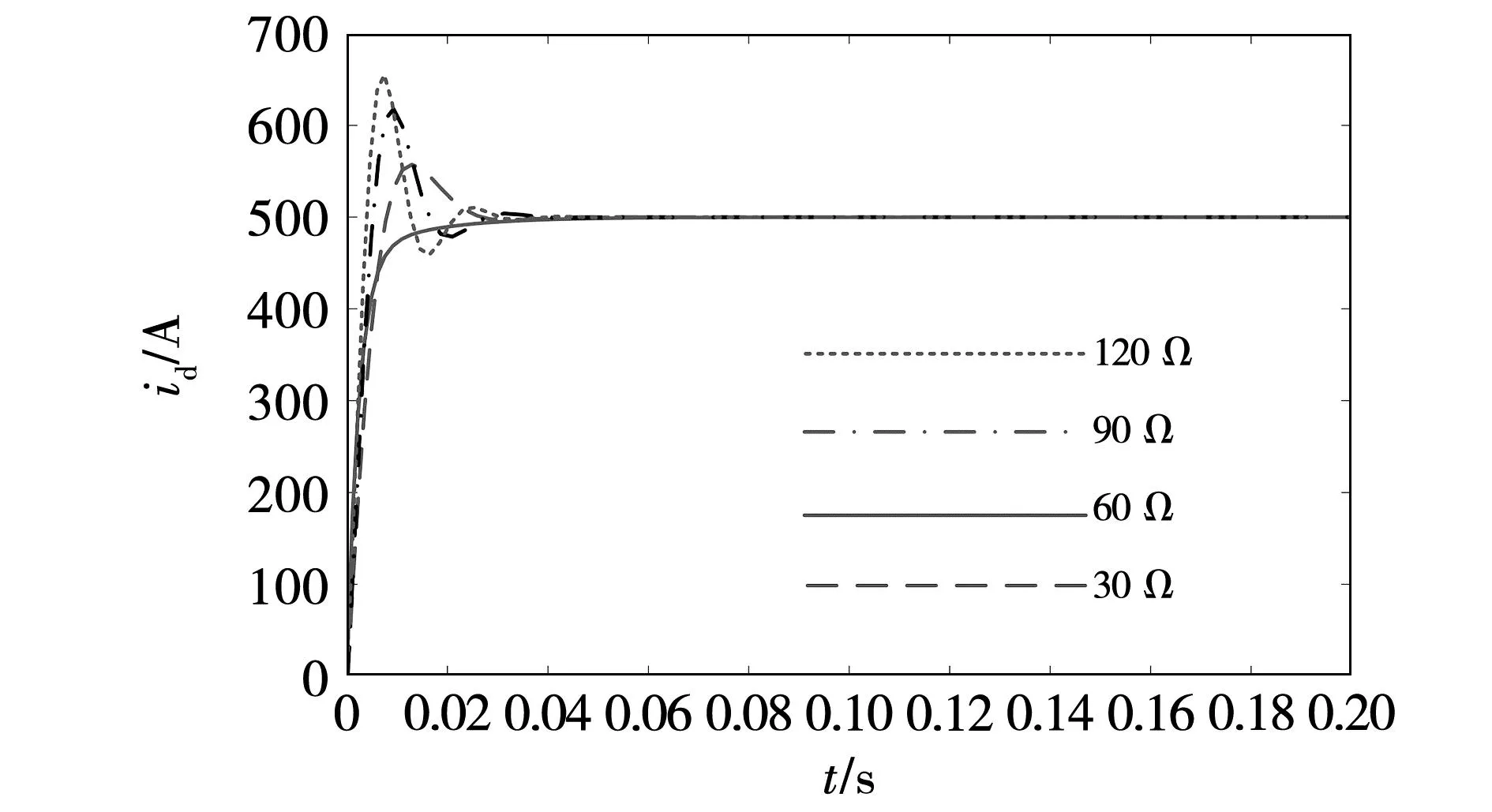
图3 不同阻尼系数下的id波形

由图可见,当R=30、90 Ω时,电流的超调大,稳定慢;而R=60 Ω时,电流的动态性能要好得多。因此,本文的阻尼参数R取60 Ω。

3.3.2 SMC控制器的调节参数的选择

图4 不同调节系数下的id波形

由图可见,当ρ=40时,超调较大;当ρ=10时,尽管超调不大,但0.03 s时出现了小幅振荡现象;当ρ=20、30时,响应快速、输出平稳,并且ρ=20时超调更小,因此,本文的SMC控制参数选取ρ=20。

4 实验结果分析

为了检验PBC-SMC控制策略的优势,本文通过MATLAB/Simulink软件构建了MMC-UPQC仿真模块,并把PBC-SMC、PBC、PID 3种控制方法对比分析。MMC-UPQC的控制系统参数如表1所示。

表1 MMC-UPQC的控制系统参数

下面对PBC-SMC控制、PID控制和PBC这3种控制方法进行了电压暂升/暂降、谐波注入、非线性负载等几种非理想电网工况实验比较。每种情况的实验结果包括7张子图。其中:图5(a)是电网电压或负载不平衡时的电流;图5(b)是PBC-SMC控制恢复后的电压或电流;图5(c)是PBC-SMC控制压控补偿电压或电流;图5(d)是PBC控制恢复后的电压或电流;图5(e)是PBC控制的补偿电压或补偿电流;图5(f)是PID控制恢复的电压或电流;图5(g)是PID控制的补偿电压或电流。

图5 电网电压不平衡下串联侧变换器的电压补偿比较

4.1 串联侧变换器的电压补偿

4.1.1 电网电压不平衡工况

设置a相电压0.02～0.08 s时上升15%,在0.12～0.18 s时下降15%,这样三相电压中a相有升降情况,三相电压出现了不平衡。在这种情况下,3种控制方法的实验对比结果如图5和表2所示。

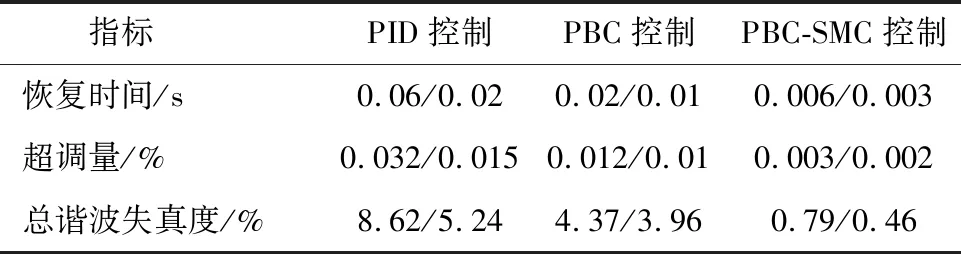
表2 电网电压不平衡下串联侧变换器的电压补偿比较

从图表可知,当a相出现上升或下降时,相比于PBC、PID两种控制,PBC-SMC控制的电网电压波动更小,PBC-SMC、PBC、PID 3种控制的稳定时间分别为0.006、0.02、0.06 s,也即PBC控制的稳定时间更短。PBC控制的电压谐波失真度(total harmonic distortion,THD)仅为0.79%,低于PID、PBC两种控制。因此,串行侧变换器采用PBC-SMC控制能够更加快速、更加准确稳定补偿电压,提高电压质量。

4.1.2 电网电压注入谐波工况

为了检测PBC-SMC控制方法的电压谐波抑制能力,本文加入了20%电网电压的3次谐波,此时THD=28%较大。此时的补偿效果如图6和表3所示。

表3 加入电压谐波时串联侧变换器的电压补偿比较

图6 加入电压谐波时串联侧变换器的电压补偿比较

从图表可知,PBC-SMC控制的补偿效果远优于PBC、PID两种控制。采用PBC-SMC控制时,0.006 s时,THD=0.88%很小,而采用PID控可降低THD,但THD=8.23%,补偿谐波还需提高。此外,PBC-SMC控制的补偿值在0.06 s时就稳定下来,而PID控制的补偿量一直波动变化。因此,相比PID控制,PBC-SMC控制能够更好地补偿电压谐波,提高电压质量。

4.2 并联侧变换器的电流补偿

图7为本文采用的非线性负载。它通过RL阻感电路串接入电阻负载。

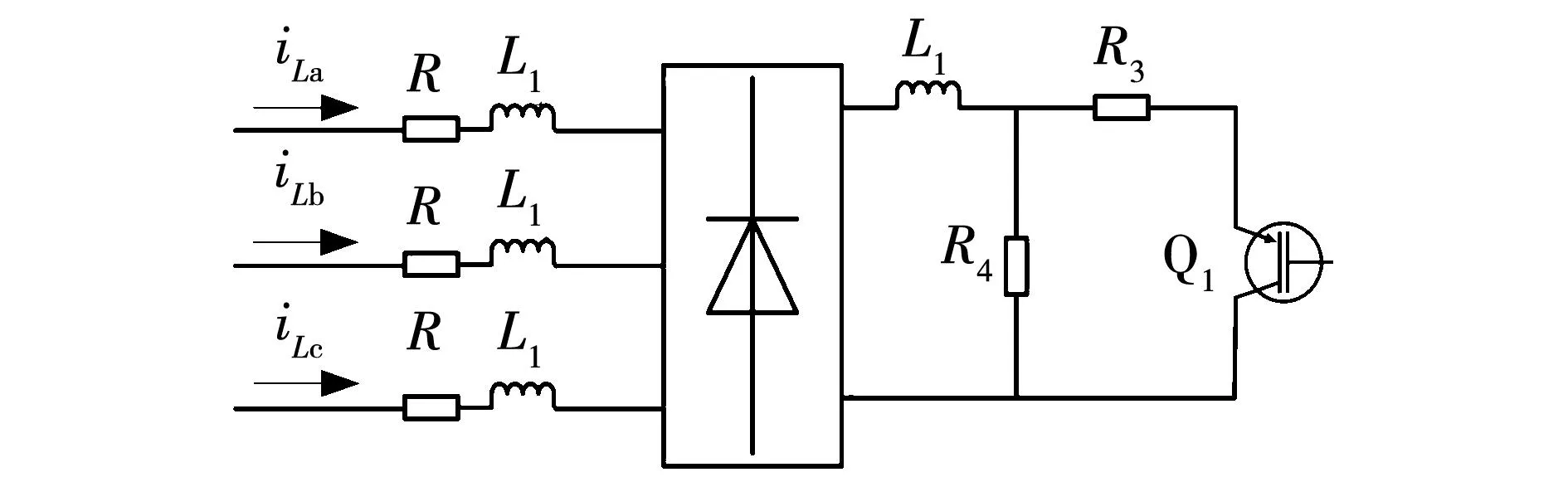
图7 并联侧变换器的非线性负载

4.2.1 非线性负载工况

若在并联侧变换器连入上面的非线性负载时,电网线路的电流谐波会较高,谐波达到THD=22.9%。非线性负载下并联侧变换器的电流补偿方法情况如图8和表4所示。

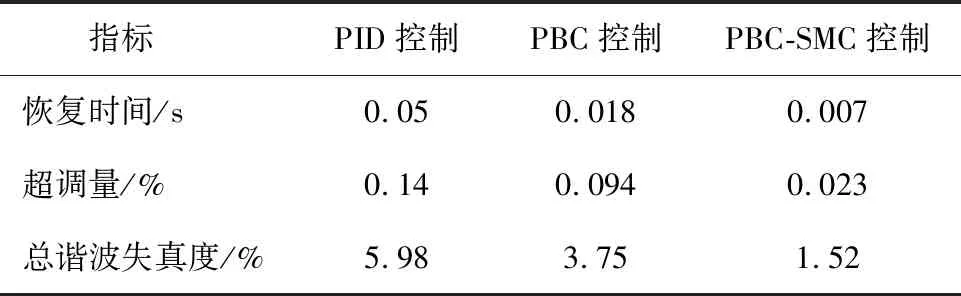
表4 非线性负载下并联侧变换器的电流补偿比较

图8 非线性负载下并联侧变换器的电流补偿比较

从图表可见,采用PBC-SMC控制时,0.007 s时电网电流就趋于稳定,而采用PID控制时,在0.05 s时电网电流才平稳。另外,PBC-SMC的波动小于其他两种控制。尽管PBC、PID两种控制能够抑制电流的谐波,但PBC-SMC控制的THD=1.52%,而PBC、PID控制的THD=3.75%、5.98%。因此,基于PBC-SMC控制的并联侧变换器电流补偿速度和补偿效果更为显著。

4.2.2 电网电压不平衡工况

当电网电压出现不平衡工况时(本文a相电网电压发生20%上升或下降),将会对负荷电流产生很大影响。因此,在电网电压不平衡时,尽快恢复电网电流很重要。图9和表5为电网电压不平衡时并联侧变换器的仿真情况。

表5 电网电压不平衡下并联侧变换器的电流补偿比较

图9 电网电压不平衡下并联侧变换器的电流补偿比较

从图表可见,采用PBC-SMC控制时,在电压暂升、暂降时的电网电流的稳定时间为0.005、0.008 s,而采用PID控制时电网电流的稳定时间为0.05 s,且PBC-SMC控制的波动和超调更小,稳定性更好;PBC+SMC、PBC两种控制的THD分别为0.84%、4.15%。因此,采用PBC-SMC控制能够更好地补偿电流谐波,提高电能质量。

4.2.3 电网电压注入谐波工况

为了检测PBC-SMC控制的电流谐波抑制能力,除采用前面图7的非线性负载引发谐波外,还在0.05 s时再加入3次谐波。图10和表6为非线性负载和加入谐波时并联侧变换器的电流补偿方法。

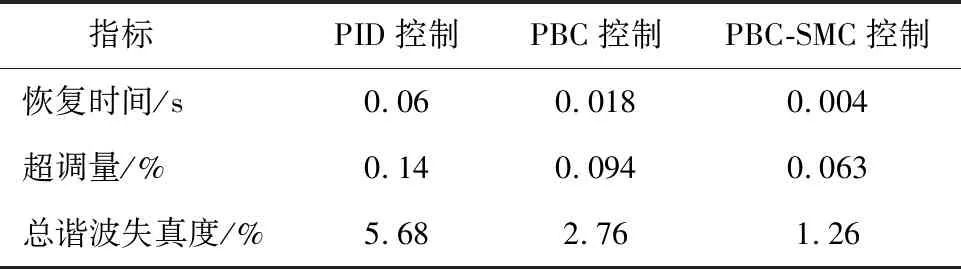
表6 非线性负载和加入谐波时并联侧变换器的电流比较

从图表可知,PBC-SMC控制的电流在0.004 s稳定,而PID控制难以很好地补偿电流,PBC控制的电流补偿质量也一般;PBC-SMC、PID两种控制的THD分别为1.26%、5.68%。因此,若有谐波出现时,PBC-SMC控制谐波抑制能力更强。

根据上述实验结果分析可知,本文所提PBC-SMC控制策略相对于PID或PBC控制策略,具有更好的补偿性能,恢复电流电压的时间更短、超调量更小、THD更低,从而使电网的电能质量更高。

5 结 论

针对MMC-UPQC系统在非理想电网电压下的电能质量补偿控制问题,本文提出了PBC-SMC策略用于解决这一问题。理论分析与实验结果表明:

1)由于PBC的参数恒定,控制系统的抗扰性和适应性不强,PBC与SMC组合的PBC-SMC控制提高了系统的适应性、抗扰性和鲁棒性;

2)与PBC、PID两种控制相比,本文提出的PBC-SMC控制响应更快、稳定性更强、电能质量补偿更高;

3)本文的MMC-UPQC的PBC-SMC控制系统能很好地解决中高压电网不理想时电能质量综合补偿问题,该系统能够很好地解决谐波注入、电网不平衡和负载非线性等工况下的补偿问题。