低速永磁同步电机转子偏心的抑制措施

韩雪岩, 王勇, 高俊

(沈阳工业大学 国家稀土永磁电机工程技术研究中心,辽宁 沈阳 110870)

0 引 言

永磁同步电动机具有效率高[1-3]、性能稳定、轻型化等优点[4-5]。永磁电机由于制造、安装不可避免的形位公差以及运行过程中电机出现的磨损会造成电机转子偏心问题。转子偏心分为三种:静偏心、动偏心、混合偏心。转子偏心会产生较大的不平衡磁拉力(unbalanced magnetic pull,UMP),会使电机振动噪声增加,严重的会影响电机结构强度,减小电机使用寿命[6-8]。因此,对永磁电机转子偏心问题的研究非常重要。

转子偏心作为永磁电机普遍存在的问题,国内外学者对转子偏心下的不平衡磁拉力、气隙磁场解析计算以及偏心故障诊断进行了深入的研究。文献[9]提出电机转子和定子的尺寸公差会导致不平衡磁拉力频谱中的附加谐波和特征谐波发生变化,指出在定义偏心检测程序时,必须将其考虑在内。文献[10]给出了静态偏心下作用在定转子上力的频率的数学表达式,通过有限元分析和实验验证了表达式的正确性,并研究了定子槽开口、绕组、永磁体厚度等对静偏心下振动的影响。文献[11]提出一种具有三层定子结构的8极12槽多自由度球形永磁电机,用拉普拉斯方法分析了电机转子偏心和不偏心时的气隙磁场,验证了拉普拉斯方法的准确性。文献[12]采用矢量磁位推导了永磁电机偏心下空载气隙磁场磁通密度的表达式,建立了一种基于边界摄动法的静态偏心解析模型。文献[13]运用解析法推导出转子发生静态偏心和动态偏心时的径向电磁力波解析表达式,经分析表明,静偏心和动偏心会产生不同的新的电磁力波分量。因而,提出一种利用振动速度频谱分析的电机偏心的快速诊断方法。文献[14]分析了混合偏心对低速大转矩永磁电机的影响,采用车削法改善了气隙磁密分布,降低了转子的疲劳寿命,但并未分析车削后不平衡磁拉力变化情况。文献[15]利用定转子辅助槽来抑制在一些特定极槽配合永磁电机中由于磁场不对称产生的不平衡磁拉力。以上文献多是采用解析法及有限元法分析偏心对电机的影响以及提出偏心的诊断方法,对偏心抑制措施的研究较少。

本文提出利用辅助槽及车削法对三种转子偏心的抑制措施。通过定子辅助槽、转子辅助槽、车削法分别对静偏心、动偏心、混合偏心进行抑制,并对辅助槽数量对UMP的影响规律进行研究,并对车削法对混合偏心的抑制进行分析。对采用三种抑制措施下的UMP值进行计算,结果表明,采用抑制措施后,转子偏心下UMP大幅下降,抑制效果显著。

1 低速永磁电机模型

本文以一台210 kW低速永磁电机为例,电机模型如图1所示,电机基本参数如表1所示。

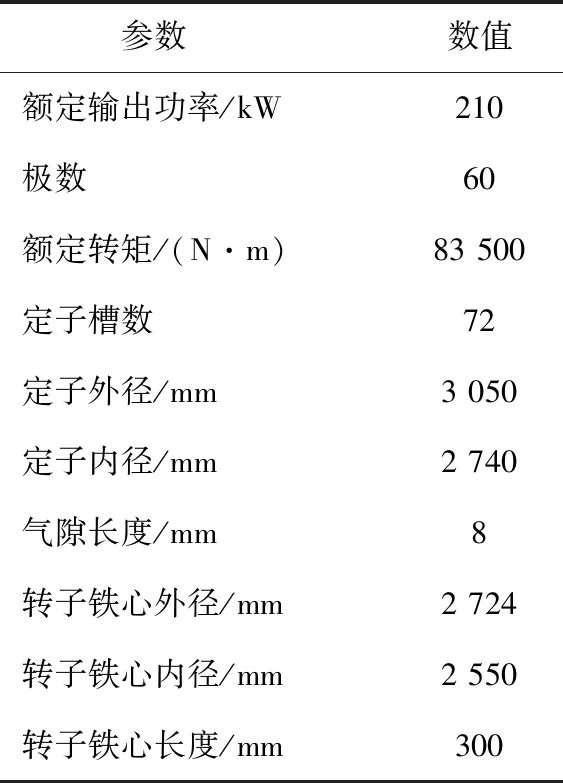
表1 低速永磁同步电动机基本设计参数

图1 210 kW低速永磁电机模型

2 转子偏心不平衡磁拉力模型

静态、动态偏心示意图如图2所示。

图2 静态、动态偏心示意图

当O′既是转子几何中心也是旋转中心时为静态偏心,当O′为转子几何中心,O为转子旋转中心时,为动态偏心。混合偏心为静态偏心与动态偏心的叠加,示意图如图3所示。

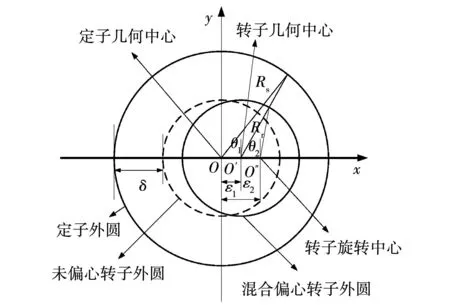
图3 混合偏心示意图

图2中:δ为未偏心时气隙长度;ε为转子偏心距离。图3中:ε1为静态偏心偏移距离;ε2为动态偏心偏移距离。

静态偏心气隙长度为

δe=δ-εcos(θ-γ)。

(1)

式中:δ为理想情况下有效的气隙长度;ε为转子偏心距离;γ为转子偏心角度;θ为空间角。

偏心下的气隙磁导分布函数为

(2)

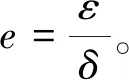
定义静态偏心和动态偏心时的磁导修正系数[1]分别为:

(3)

(4)

混合偏心气隙长度为

δ′=δ-ε2(cosθ1+cosθ2)-ε1cosθ1。

(5)

式中:δ′为混合偏心时气隙长度;ε1为静态偏心偏移距离;ε2为动态偏心偏移距离;δ为理想状态下气隙长度;θ1为静态偏心气隙位置角;θ2为动态偏心气隙位置角。

混合偏心时气隙磁导的分布函数为

(6)

定义混合偏心时的磁导修正系数为

(7)

永磁电机中,气隙磁通密度表示为

B(θ,α)=F(θ,α)λ(θ)。

(8)

偏心下的气隙磁通密度为:

Bs(θ,α)=EδsF(θ,α)λ(θ);

(9)

Bd(θ,α)=EδdF(θ,α)λ(θ);

(10)

Bm(θ,α)=EδmF(θ,α)λ(θ)。

(11)

由文献[16]可知,任一位置的径向力密度可以表示为

(12)

式中μ0为真空磁导率。

用Cartesian坐标分析求解,任一位置的局部径向力密度可分解为x轴分量、y轴分量,表达式为:

(13)

对局部磁拉力密度进行积分,得到总的磁拉力为:

(14)

将式(9)～式(13)代入式(14)中可得3种偏心下的不平衡磁拉力分别为:

(15)

(16)

(17)

由式(15)～式(17)可以看出,转子偏心下的UMP与永磁体磁动势以及气隙磁导有关,转子发生静态、动态、混合偏心时主要引起气隙磁导发生变化。因此,本文提出的辅助槽、车削法主要是通过改变气隙磁导,从而达到对转子偏心的抑制。

3 抑制措施

本节主要研究在转子偏向侧开定子辅助槽、转子辅助槽(包括槽位置、槽高、槽宽、槽数量)以及车削法分别对静态、动态、混合偏心的抑制效果。

3.1 静态偏心抑制措施

静态偏心特点为最大、最小气隙位置不随转子转动发生改变,因此选择在小气隙侧开定子辅助槽对静态偏心进行抑制,如图4(a)所示。辅助槽示意图如图4(b)所示。

图4 定子辅助槽示意图

图4(b)中,h1为槽高,w1为槽宽,θ1为槽位置,齿部中线与槽宽中线重合时为0位置,槽宽中线在齿部中线左侧θ1>0,否则θ1<0。

槽位置、槽深、槽宽、槽数量对静态偏心下UMP的影响如图5～图8所示。开辅助槽定会引起空载反电势的变化,因此图5～图8中也给出了空载反电势的变化情况。

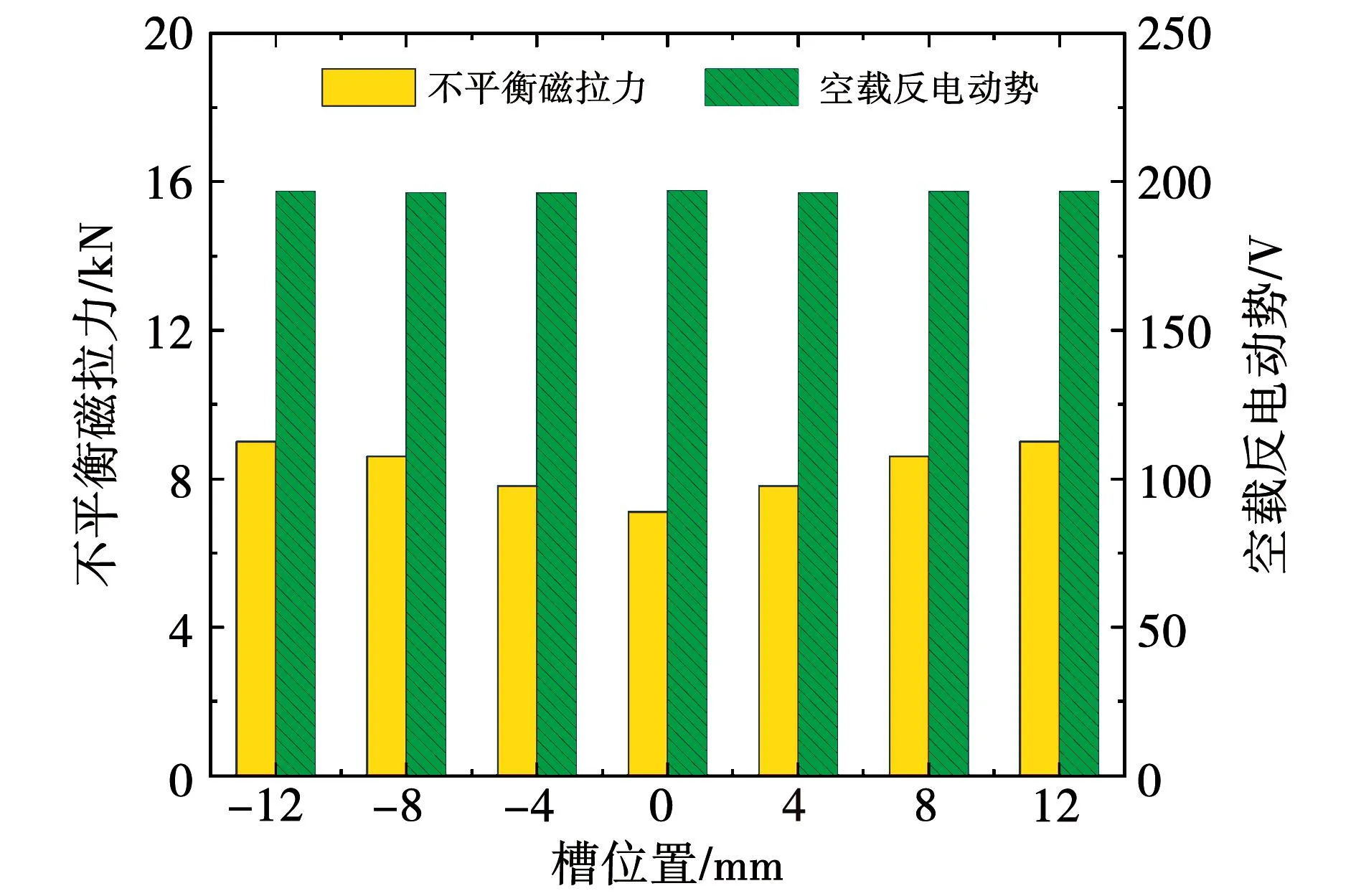
图5 槽位置的影响

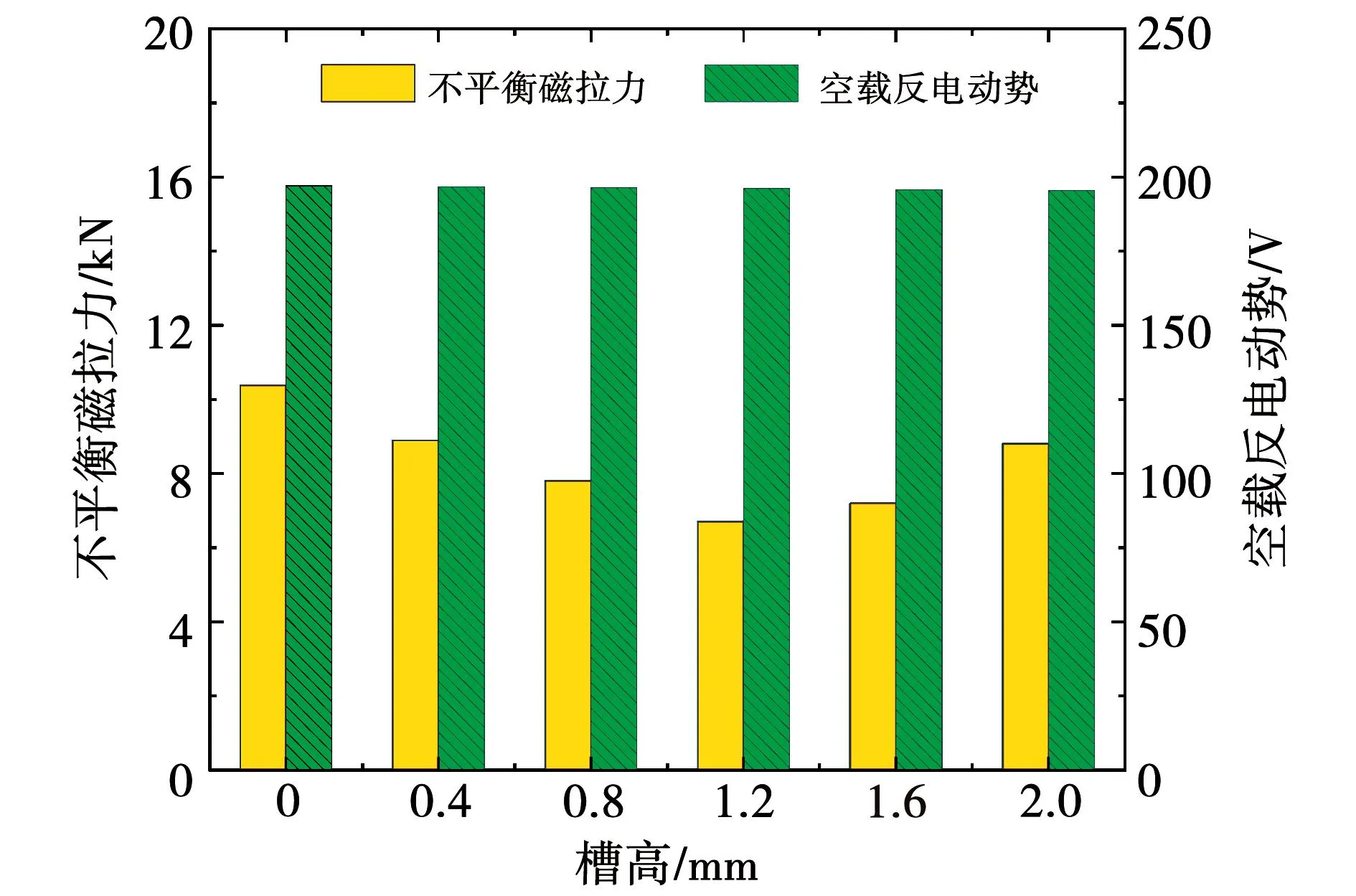
图6 槽高的影响

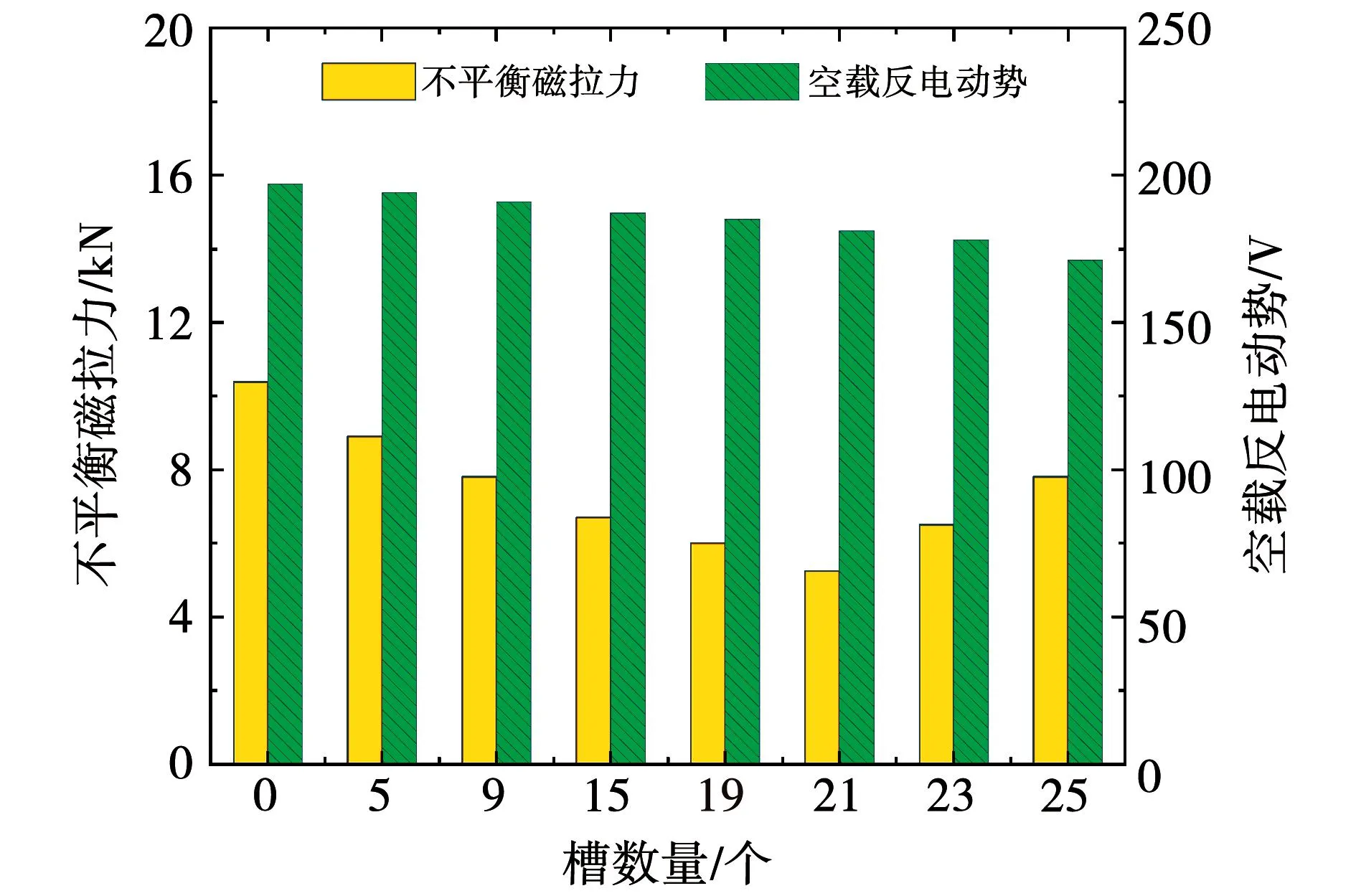
图8 槽数量的影响

从图5～图8中可以看出,辅助槽在0位置,槽高为1.2 mm,槽宽为30 mm,槽数量为21个时,对静偏心下UMP抑制效果最明显。辅助槽开在定子齿部中间位置抑制效果最好,槽高、槽宽选取的合适才能减小UMP值。随着辅助槽数量增加,UMP值随之减小,当数量达到21个时,UMP值逐渐增加。槽位置、槽高对空载反电动势的影响较小。槽宽、槽数量的增加对等效气隙长度有影响,因此对空载反电势的影响略显著。随着辅助槽宽度及数量的增加,空载反电势值有明显的下降趋势,辅助槽尺寸的选择要充分考虑槽宽、槽数量对反电势的影响。

采用定子辅助槽前后,偏心率为10%的静偏心下UMP对比曲线如图9所示。静偏心下UMP的最大值由原来的10.38 kN下降到5.21 kN,下降了49.8%。

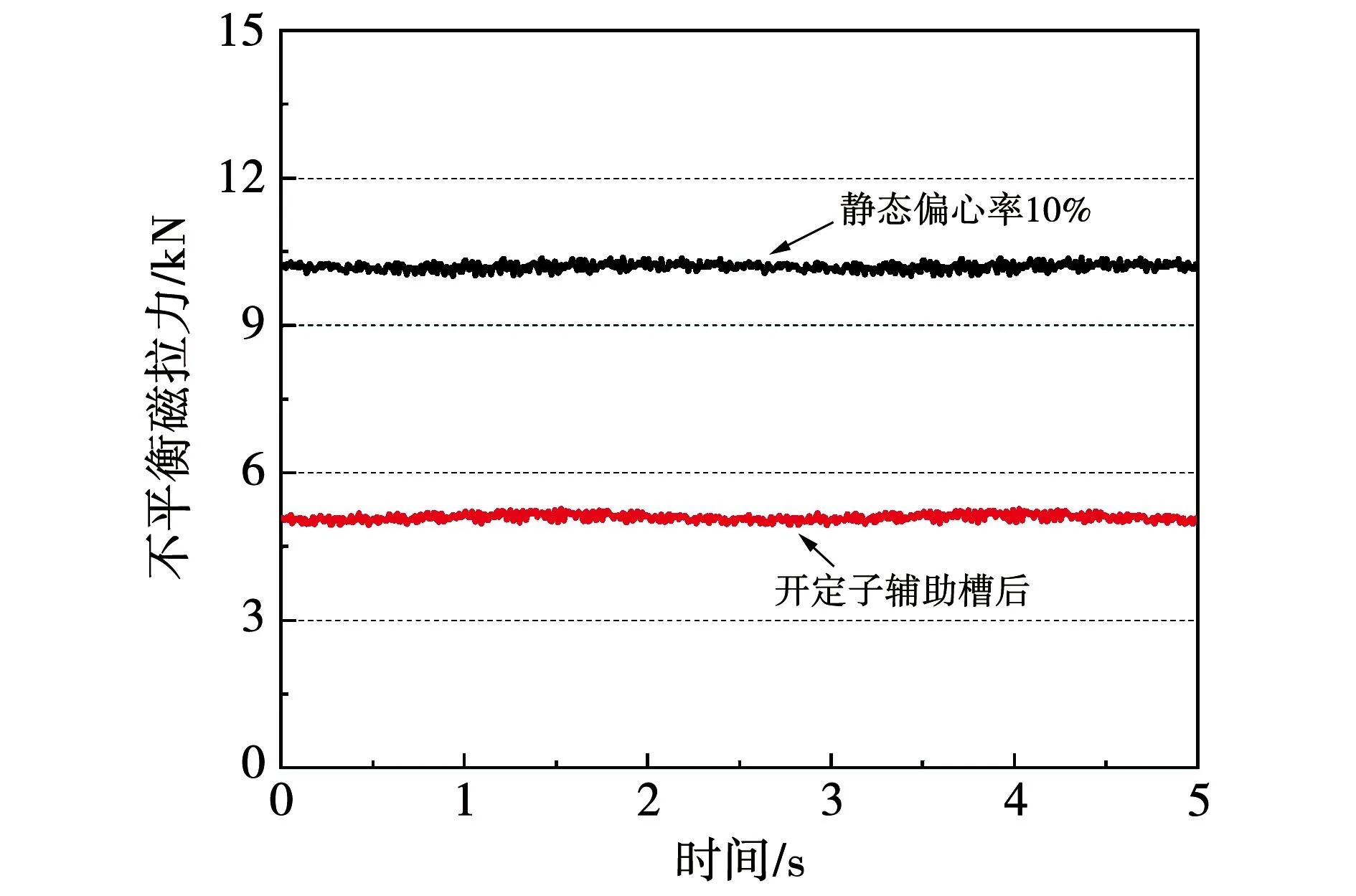
图9 定子辅助槽对静态偏心的抑制效果

3.2 动态偏心抑制措施

动态偏心的特点为最小气隙位置随着转子转动发生改变,因此选择在小气隙处开转子辅助槽对动态偏心进行抑制,如图10(a)所示。辅助槽示意图如图10(b)所示。

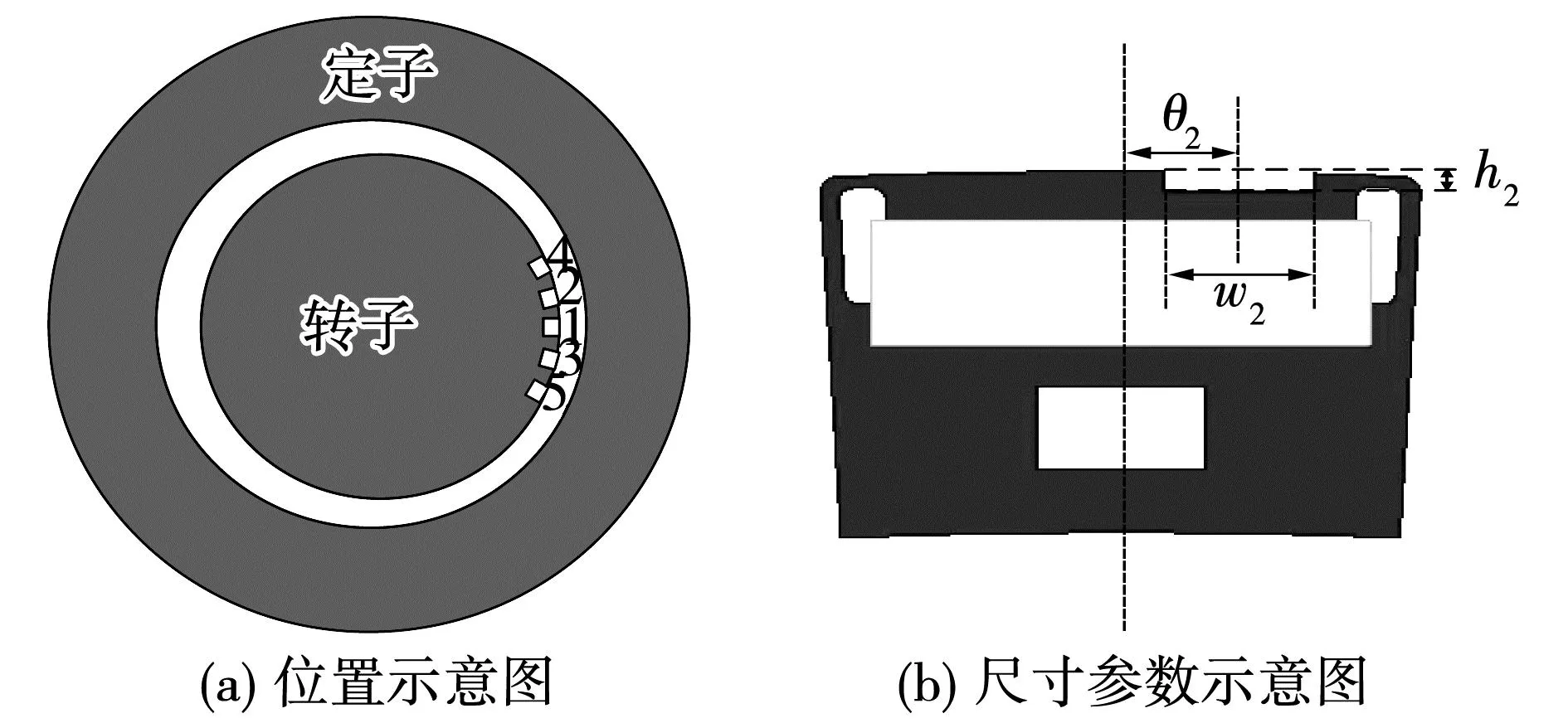
图10 转子辅助槽示意图

图10(b)中:θ2为槽位置;h2为槽高;w2为槽宽。槽位置定义与定子辅助槽相同。

辅助槽尺寸及数量对动偏心下UMP的影响如图11～图14所示。

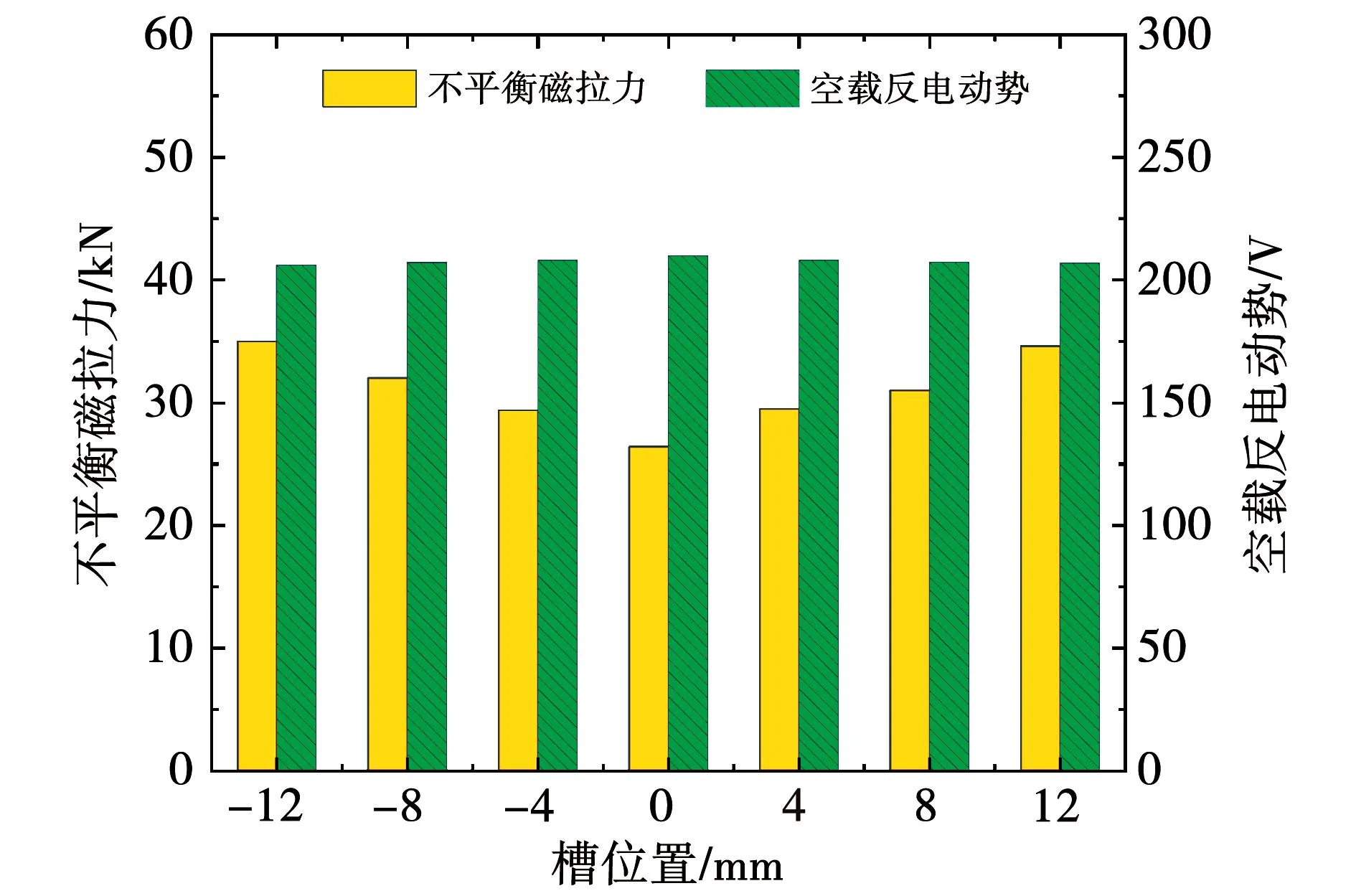
图11 槽位置的影响

图12 槽高的影响

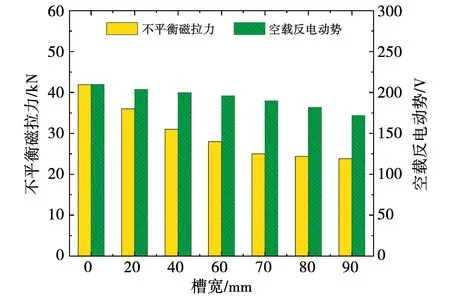
图13 槽宽的影响

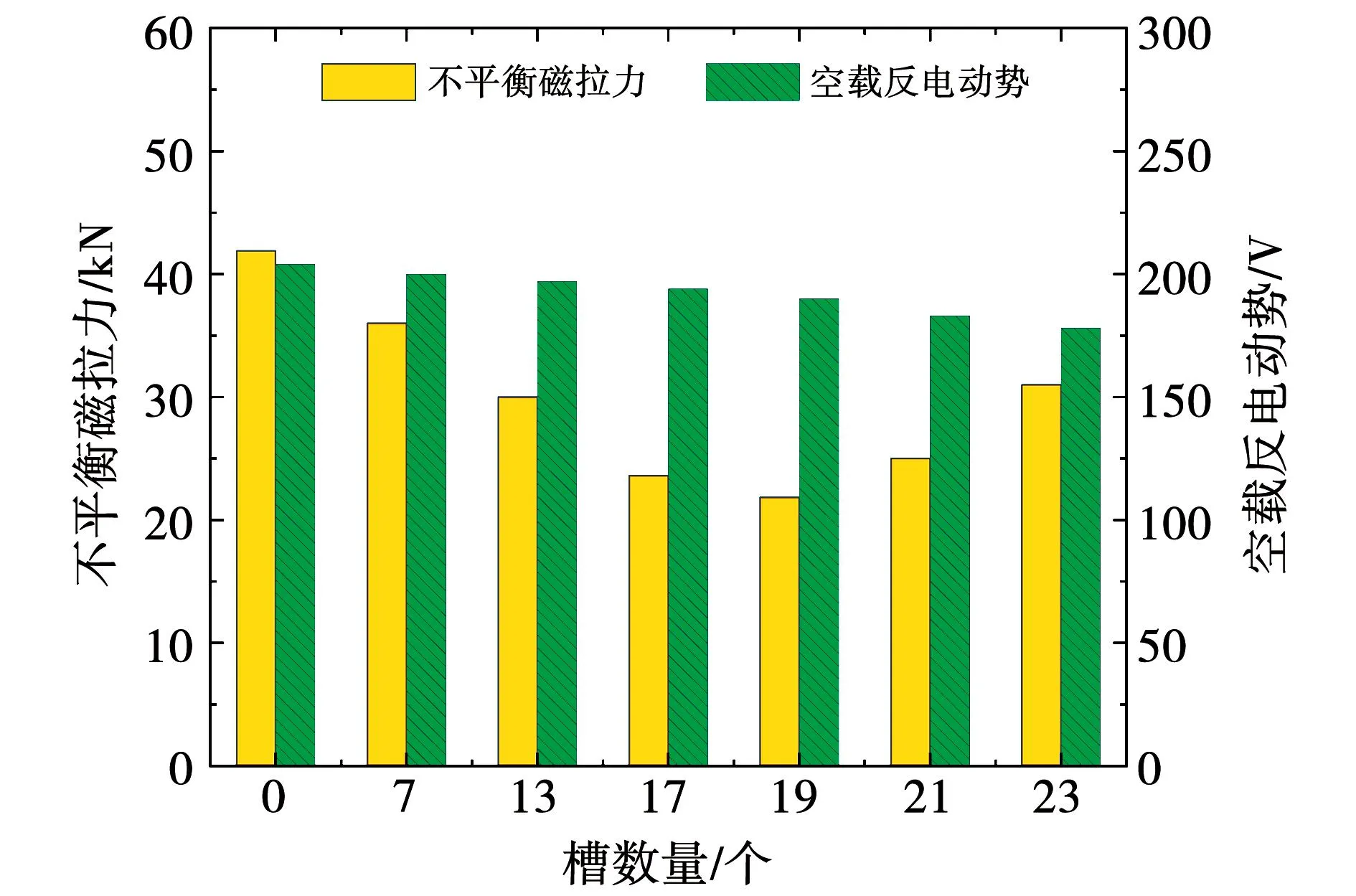
图14 槽数量的影响

本文研究所用电机转子为分块结构,从图11～图14可以看出,辅助槽位置在每块转子中间位置时,对动偏心下UMP抑制效果最好。槽高为7 mm时,UMP值最小。随着槽宽的增加,UMP值随之下降,槽宽达到70 mm后,下降趋势减缓。考虑到槽宽对空载反电势的影响,本文所研究电机的槽宽选取在70 mm左右最为合适。槽数量对空载反电势也有影响,数量增加,反电势值下降。因此,对动态偏心下UMP的抑制要考虑到空载反电势的变化。本文所研究电机的槽数量选取在19个最为合适。

采用转子辅助槽前后,偏心率为40%下的动态偏心的UMP曲线对比如图15所示。采用转子辅助槽后动态偏心下的UMP最大值由原来的41.9 kN下降到22.1 kN,下降了47.2%。

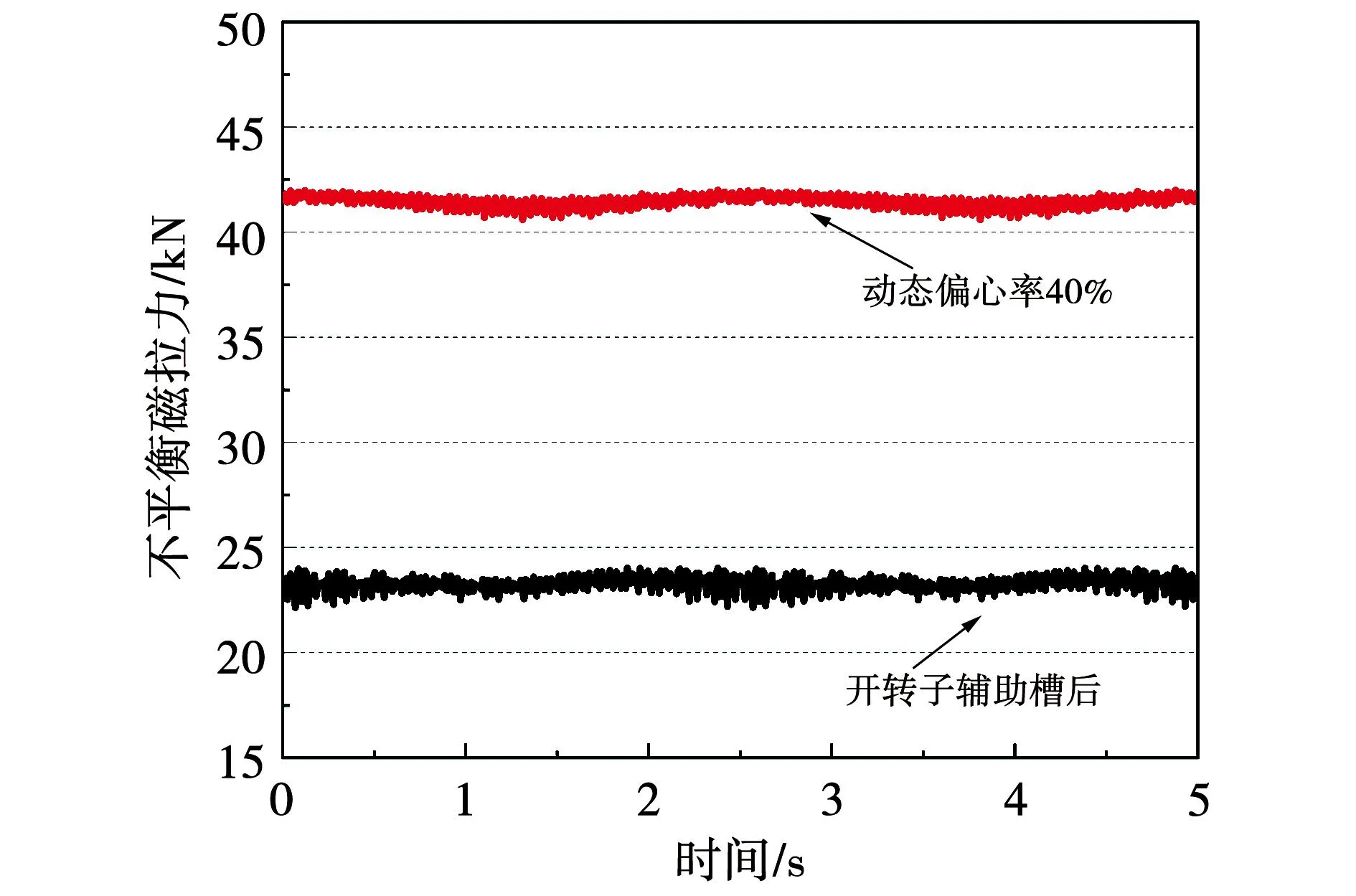
图15 转子辅助槽对动态偏心的抑制效果

3.3 混合偏心抑制措施

混合偏心为静偏心与动偏心的叠加,最大最小气隙位置随转子转动作不规则周期性变化。本文采用车削法对混合偏心进行抑制。车削法示意图如图16所示。

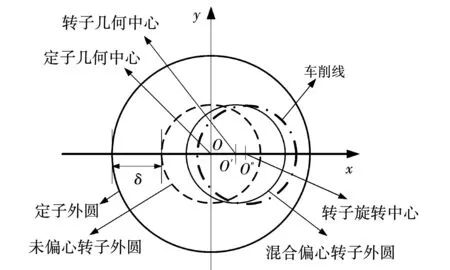
图16 车削法示意图

混合偏心时,转子几何中心与旋转中心不重和,以旋转中心为原点作与转子半径相同的圆,如图16中点划线所示,将点划线外的转子部分车削。

车削转子主要对等效气隙长度有影响,因此对车削后的空载反电势进行计算,转子未发生混合偏心以及发生混合偏心车削前后空载反电势变化情况如表2所示。

表2 空载反电势变化

车削转子前后,混合偏心下UMP曲线如图17所示。可以看出,车削后UMP最大值由原来的76.8 kN下降到13.86 kN,下降81.95%。

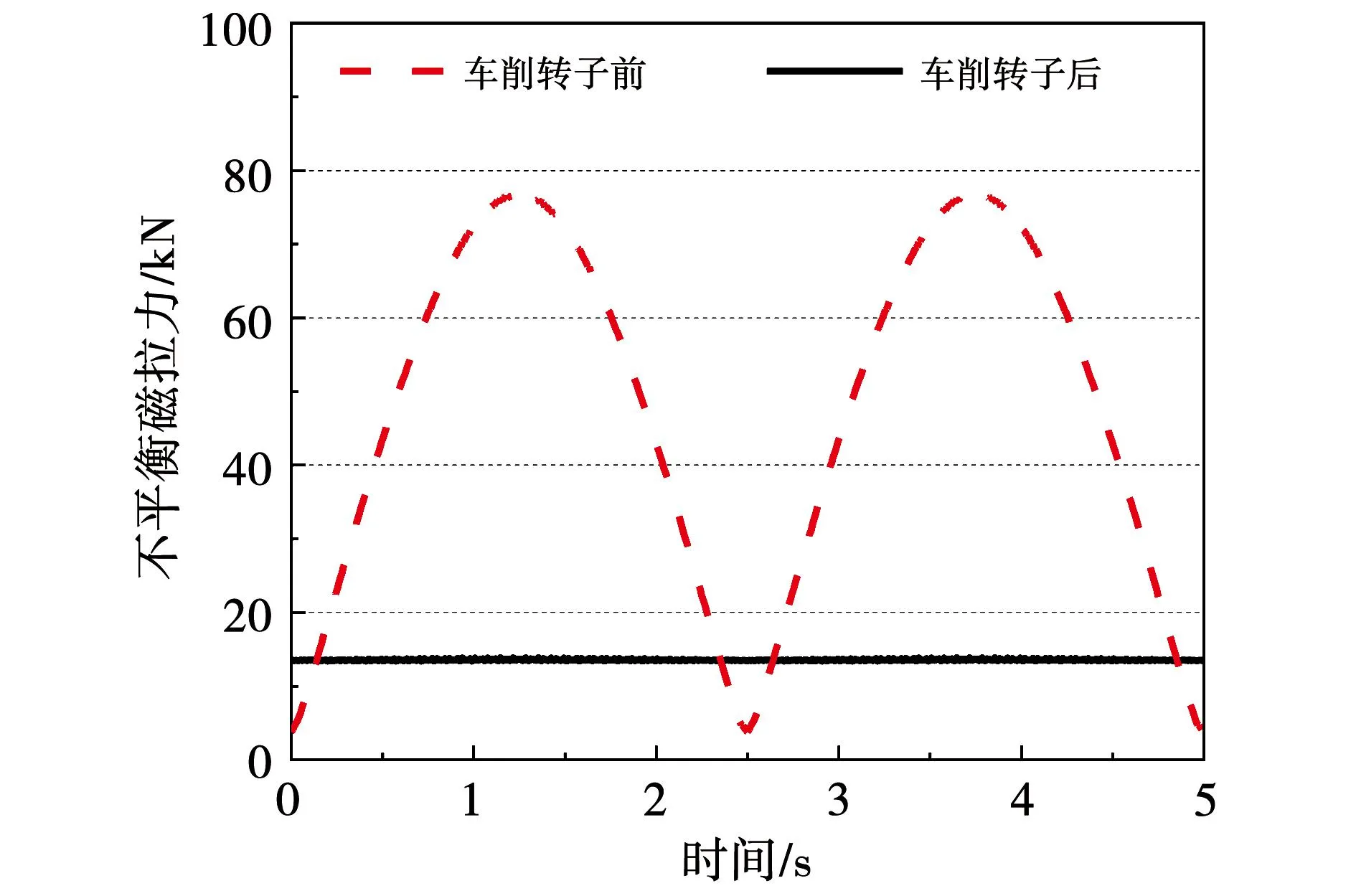
图17 车削法对混合偏心的抑制效果

4 结 论

本文以一台210 kW低速永磁同步电机为例,基于对转子偏心下不平衡磁拉力模型的分析,提出分别针对静偏心、动偏心、混合偏心的抑制措施——定子辅助槽、转子辅助槽、车削法。对辅助槽尺寸及数量、车削转子对偏心下UMP的影响进行研究,并得出以下结论:

1)在转子偏向侧开定子辅助槽可以有效抑制静态偏心产生的UMP,采取抑制措施后静偏心下UMP值下降49.8%。

2)在转子偏向侧开转子辅助槽可以有效抑制动态偏心产生的UMP,采取抑制措施后动偏心下UMP值下降47.2%。

3)车削转子可以有效抑制混合偏心产生的UMP,采取抑制措施后混合偏心下UMP值下降81.95%,空载反电势值下降4.22 V,在允许范围内。