一种多模型融合的风电系统永磁同步发电机数字孪生建模方法

刘利强, 尹彦博, 齐咏生, 李永亭

(1.内蒙古工业大学 电力学院,内蒙古 呼和浩特 010080; 2.内蒙古自治区电能变换传输与控制重点实验室,内蒙古 呼和浩特 010080; 3.内蒙古自治区机电控制重点实验室,内蒙古 呼和浩特 010051 )

0 引 言

数字孪生技术(digital twin,DT)在被提出开始,便受到了电力设备状态监测和故障诊断领域的广泛关注。随着传感器、模型仿真、物联网等相关技术的不断完善与成熟,将DT应用于风电机组的状态监测与故障诊断已成为当前的研究热点[1]。

目前国内外学者已分别在风电系统不同部件中进行了关于风机DT技术应用的研究。文献[2]以风机齿轮箱为例提出了根据实时数据、历史数据等,对风机进行多维虚拟模型构建,完成对物理风机的虚拟映射。并通过物理风机与虚拟风机的同步运行与交互,进行物理与仿真数据融合分析及应用的五维建模思路。在风机的传动系统方面,布鲁内尔大学研究团队提出了一种实时、交互式且动态的神经网络孪生模型,用于风机轴承的状态监测[3]。在风机的电力电子器件方面,奥尔堡大学研究团队提出了一种基于数字孪生的功率变换器状态监测方法。构建了器件的数字孪生模型,并应用了粒子群优化算法实现对物理实体内部参数更新优化,以最大程度地减少孪生模型与其物理实体之间的差异[4]。综上可知,目前针对风电系统设备数字孪生的研究虽已取得一些成果,但对风电系统发电机的研究鲜有报道。发电机作为风电系统的核心部件,其健康状态的正常与否影响着整个系统的稳定运行。然而由于发电机设备原理复杂、关联系统较多、各物理场之间联系紧密等因素,导致针对发电机部分的数字孪生的研究成为了当前研究的重点与难点。因此进行针对风电系统发电机设备的数字孪生相关技术研究对风力发电领域数字孪生技术的发展与应用有着重要的价值。

目前对于风力发电系统DT技术的研究虽然有了一定的进展,但实例化的应用尚未获得实现,且该技术背后的传感器、模型仿真、虚实互联等关键技术均未实现突破。尤其在建模相关技术的研究中,鉴于数字孪生技术要求虚拟模型具备“完全”映射物理实体的特点,进而使得对孪生模型有了多物理场、多耦合、多集成以及实时性等需求[5]。然而当前针对风电系统的建模多是基于MATLAB/Simulink的数学模型,这类模型虽然具有结构简洁、逻辑清晰等优势,但对于系统中发电机设备无法做到细致建模,使得设备的虚拟模型存在着过于理想化和标准化的不足,尤其对于发电机这样的复杂机电设备,简单的数学模型无法满足实现数字孪生的需求[6]。在诸多关于数字孪生虚拟模型建模技术的研究中,文献[7]构建了基于GA-BP神经网络的光伏功率预测孪生模型,将气象数据作为输入进行计算,从而得到预测初始值。该建模方法虽然智能简便,但难以对发电机设备的内部物理特性进行分析。文献[8]则借助有限元分析软件COMSOL创建了变压器的数字空间模型;基于变压器实际运行条件,通过模拟变压器不同运行条件,对其进行电热特性分析,并与国标导则对比完成孪生模型的验证。虽然针对设备本体的有限元模型可以做到对发电机设备的精细化设计和内部多物理场分析,但由于风电系统发电机设备受风力机、控制系统的影响不可忽视,因此这类建模方法在考虑系统耦合方面存在欠缺,同时有限元模型在保证计算精确度的同时往往会使计算速度变得缓慢,这与DT模型实时性的理念相悖[9]。另外,常规的建模平台不具备部署物联网的能力,使得所建虚拟模型无法实现后期与实体风机的数据交互及融合分析。

为解决上述风电系统发电机设备基于DT建模技术的不足,以2 MW永磁同步发电机(permanent magnet synchronous generator,PMSG)为研究对象,采用Maxwell 2D对电机本体及电磁模型进行构建。为考虑系统对电机的影响,根据风电系统结构在DT建模平台搭建外电路,在DT模型建模平台中搭建控制电路并对二者进行联合仿真,以实现场路耦合。基于上述模型,对PMSG进行瞬态热分析,此外,为解决有限元分析流程复杂,计算缓慢的不足,引入一种改进的PSO-SVM的代理模型构建方法,针对粒子群算法局部收敛问题,结合差分变异策略,提出使用信息熵作为变异判据的方法,对PSO算法进行改进,进而对SVM惩罚因子和核参数进行优化。最终将降阶模型集成至DT建模平台完成PMSG数字孪生模型的搭建。通过模拟不同工况,对该模型物理特性进行验证分析。最后,利用实体风机SCADA运行数据对DT模型进行了有效性验证。

1 风电系统PMSG模型

1.1 PMSG二维电磁场模型

PMSG作为具有电磁特性的典型能量转换装置,可通过麦克斯韦方程组对其内部电与磁场进行关联。为使场量与场源之间的物理概念清晰,常引入有旋磁场矢量磁位A以减小未知数的量,考虑二维情况下只有Z轴分量的特点。则有直角坐标系下

(1)

式中:Jsz为电流密度;v为电机磁导率。由于孪生模型要求电磁模型提供PMSG的损耗、磁链等计算参数,以支撑场路耦合与磁热耦合的计算分析,需考虑求解域内媒质运动情况。因此,电机二维动态电磁场控制方程为

(2)

1.2 PMSG控制系统

如图1所示风电系统PMSG的控制系统主要由PMSG、PWM机侧变流系统、风力机模型、双闭环控制电路组成。

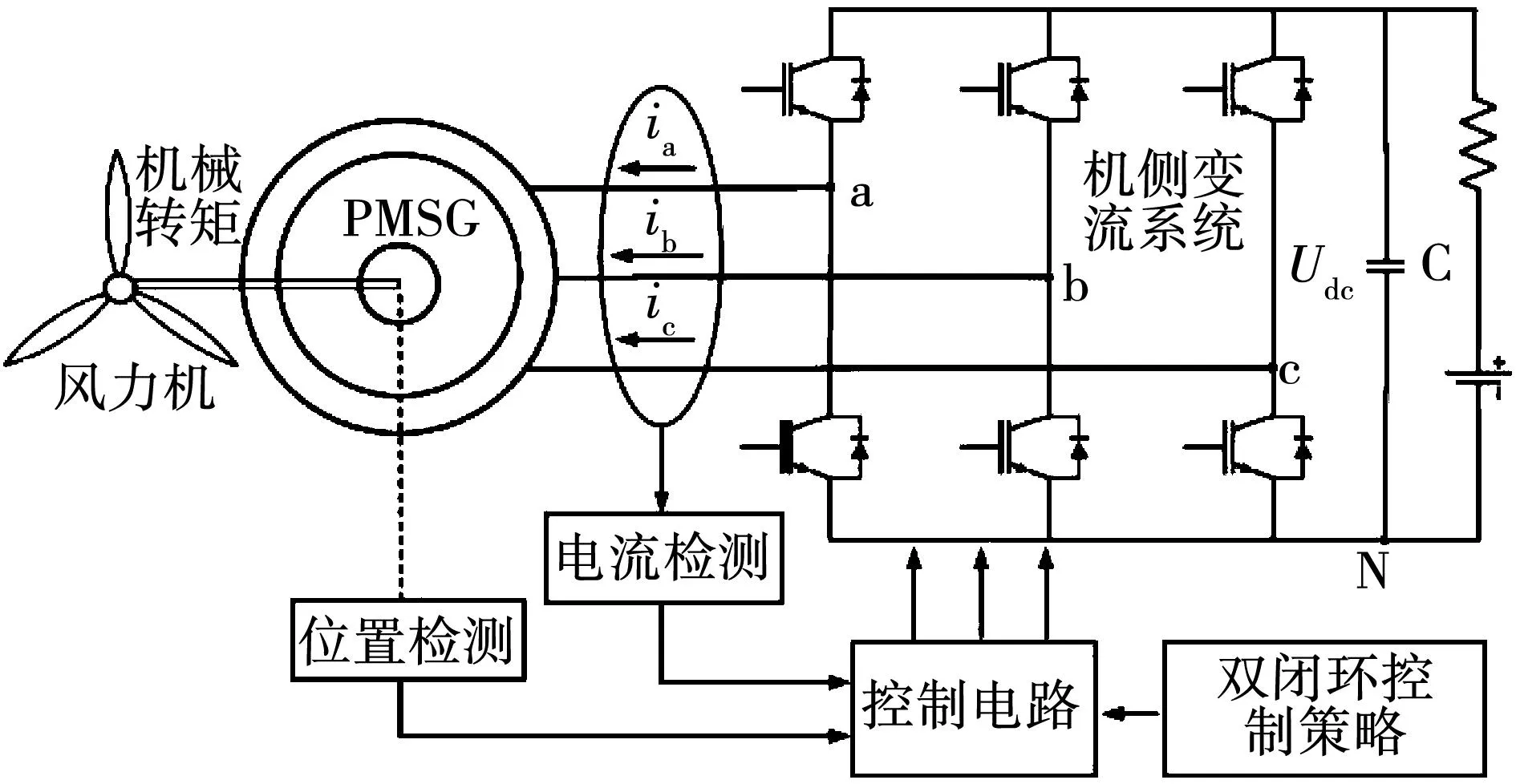
图1 机侧PWM变流系统结构图

直驱风电系统风力机的作用是将风能转换为机械能,为PMSG提供机械转矩从而带动电机转子转动。风轮输出机械功率和转矩为:

(3)

式中:Pwt为风轮机械功率;Twt为机械转矩;ρ为空气密度;R为叶片半径(m);CT、Cp分别为风轮功率系数和转矩系数;λ为叶尖速比;β为桨距角。

图2 双闭环控制策略 Fig.2 Double closed-loop control strategy

1.3 PMSG磁热耦合模型

针对永磁同步发电机三维瞬态温度场有限元分析,数学模型根据传热学理论建立,以描述物体温度变化规律,其中三维瞬态方程可表示为

(4)

式中:T为物体待求温度;λx、λy、λz分别为求解域内各种材料沿不同方向的传热系数;qv为电机内各损耗产生的内热源热功率;ρ、c、τ分别为密度、比热容和时间。电机的温升不仅取决于发热,而且要考虑散热的影响。以热媒为传热载体的辐射散热和以空气为载体的对流散热是PMSG的主要散热方式,由于辐射散热系数相比于对流散热系数而言相对较小。因此,本文不考虑辐射散热对于电机散热的影响。对流散热系数的确定与PMSG散热方式相关,由于本文所研究直驱风电系统采用风冷冷却方式,则风电系统PMSG对流散热系数可表示为

(5)

2 基于数字孪生技术的建模方法

数字孪生技术对虚拟模型的本质要求是能够将运行参数映射到模型中,并通过在虚拟模型中的仿真获得不同工况条件下的PMSG特征参量,进而准确反映或推演物理实体设备的运行情况及关键物理场特性。为实现这一目标,本文通过构建2 MW PMSG电磁模型、外电路模型、磁-热耦合模型,进而实现DT模型的磁-路-热耦合。考虑到DT模型后期需要部署至云平台与实体设备进行数据实时交互及故障诊断、健康预测等相关应用,因而对于模型的系统集成及实时计算能力具有较高要求。因此,本文采用代理模型代替原有复杂的磁-热耦合有限元模型,可有效提升运算效率和实时性;之后,采用可与物联网实现部署交互的DT建模平台进行集成。如图3所示,为构建孪生模型的总体算法框图。

图3 基于数字孪生技术的PMSG建模流程图

由图可知,孪生模型构建过程主要包括4个模块,分别为:1)建立2 MW PMSG电磁模型;2)建立2 MW PMSG外电路及控制电路;3)建立磁-热耦合模型;4)基于改进的PSO-SVM方法对热模型进行降阶并集成。该方法能够实现设备物理属性与系统控制的兼顾与融合,具备实体与虚拟模型数据的实时交互能力。

2.1 电磁模型建模

电机本体及电磁模型的作用是能够反映实体电机的几何构造及物理属性。因此,对于PMSG电磁模型的创建需要依据可靠的电机几何参数和准确的电磁场分析计算。结合实际风机实体指标数据和已经验证的实体样机几何数据,利用电机有限元电磁分析软件Maxwell对2 MW永磁同步发电机数字孪生模型电机本体进行设计,参数如表1所示。电磁耦合模型的研究对象为定子与转子部分,PMSG类型为表贴式,由于是兆瓦级发电机,因此绕组形式采用分数槽。求解域的确定则根据计算效率高的需求,并结合磁场分布特性,确定选取二维模型的1/12圆周来表示[11,17]。由于三角形网格剖分对于二维模型的描述有着细微平滑的优点,因此对PMSG定转子各部进行剖分时采用此类型网格。同时,为避免计算时每个离散单元的误差影响计算精确度,网格密度不宜过大。根据经验,发电机定转子铁心部分密度为6 mm,定子绕组部分为7 mm,磁钢部分为3 mm。所设计的PMSG二维电磁场模型及网格剖分图如图4所示。

表1 2 MW PMSG设计参数

图4 PMSG 有限元模型

2.2 外电路及控制电路建模

外电路及控制电路模型作为虚拟模型实现电磁与磁热模型与外部控制电路耦合的核心,其作用是向PMSG提供机械转矩,控制电机转速及转矩实现功率控制、整流逆变稳定并网等。因此在DT虚拟模型建模平台需完成2 MW PMSG的主电路和控制算法,该平台具备多学科领域元件库可满足系统级的动态建模、仿真[18]。本文建立的PMSG主电路包括三相逆变电路及与电机电磁模型联合仿真集成部分。由于DT虚拟模型只针对PMSG本体故仅对变流系统机侧部分进行搭建,因此,直流母线直接给定直流电压源1 100 V以等效直流母线电压,功率开关器件S1～S6采用IGBT,SVPWM信号调制模块采用平台已封装模型。将通过SVPWM模块中得到的三相PWM信号输入到IGBT中。主电路中加入电流、转速等测量元件。在电磁模型机械输入端设置转动惯量及转矩源。由于二维电磁场模型无法对发电机定子端部绕组进行建模,因此,需要加入定子电阻和端部漏感来等效电机定子的端部效应,从而保证场路耦合计算的精确性。

控制电路由风力机模型、转速和电流双闭环控制电路构成。如图5所示。当风电系统处于变功率输出阶段时,风力机模型根据风速和桨距角的输入,基于前述风力机数学模型计算,输出转矩。发电机转速指令由控制器给定,机侧变流器负责控制跟踪给定转速。为了实现最大功率跟踪,使用查表法,利用最大功率曲线,查出风速对应的最佳转速,将其作为给定值输入转速外环。通过双闭环控制策略生成定子d-q轴给定电压。然后,将转矩、电压信号经平台联合仿真接口输入至DT建模平台分别向PMSG提供转矩和生成IGBT驱动信号的电压信号。最终,PMSG经所提供的转矩输入后起动,计算过程中测量原件将测得的电流、转速、位置角信号导入到控制电路中,实现数据的交互,完成PMSG相关电磁特性与运行特性的计算[19]。

图5 控制电路图

2.3 PMSG热模型

PMSG几何模型和热源损耗是热模型构建的基础,其中,几何模型由电磁模型部分提供,根据实体样机资料,设置材料属性。其中定转子铁心部分为结构钢,绕组为铜导线,永磁体材料选择为钕铁硼45SH。为保证计算结果的准确,对定子槽部、气隙等温度变化剧烈的区域进行加密。电机的热源损耗是发电机温度升高的根源,PMSG的损耗热源包括定子绕组导体的铜耗、定、转子铁心齿部与轭部产生的铁耗和涡流损耗等,这些不同工况条件下的热源通过外电路及控制电路的相关设置,对电磁模型进行计算获得。基于上述模型提供的几何模型和相关热源计算,对2 MW PMSG数字孪生模型热模型部分进行建模。首先根据电机材料属性及结构确定铁心、绕组、永磁体等各部分的导热系数。发电机各部分导热系数如表2所示,发电机定子表面与外界空气的散热系数根据不同风速条件通过计算获得。由于电机运行期间定转子间发生相对运动,因此需采用等效热对流系数,来简化并替代定转子气隙间发生复杂的热对流效应[13～16]。

表2 PMSG各部分导热系数

2.4 模型降阶

利用上述有限元方法进行热模型的计算,虽然更精确、直观,但也有着构建流程复杂和计算缓慢的不足,与数字孪生技术要求不符。为解决高阶复杂的虚拟模型能够在保证多物理场计算精确度的同时又满足实时性的要求,基于机器学习的模型降阶技术成为了解决这一数字孪生建模环节技术难题的热门方案之一[20]。为此,引入一种PSO-SVM的融合算法实现模型降阶,该算法兼备PSO的寻优准确和SVM的小样本预测优点。然而在算法运行过程中发现,PSO算法容易陷入局部最优解,导致常常出现局部收敛问题。为此,提出采用信息熵结合差分变异中的变异策略来解决该问题,它可以有效克服PSO算法在后期迭代中种群多样性迅速降低的缺陷。优化过程如图6所示。

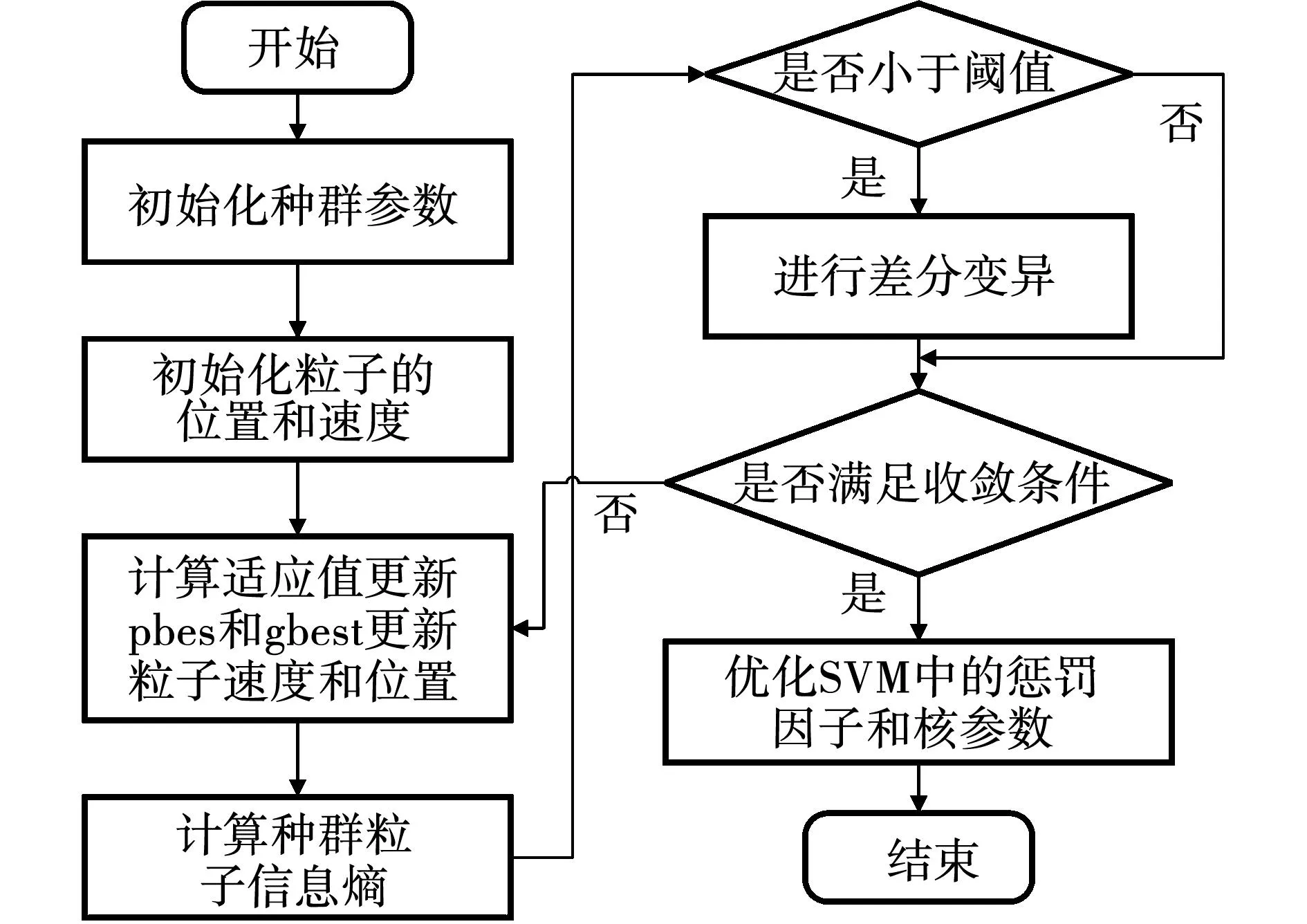
图6 代理模型搭建过程

由图6可知,当引入信息熵后,通过计算种群的信息熵并对比设定阈值,可使种群自动判别是否需要进行差分变异,从而避免种群重复变异,在提升计算效率的同时保证粒子群算法陷入局部最优解。其中信息熵数学表达式为

(6)

式中:U为信源符号;pi为不同信源符号所对应的概率。对数的底根据经验取2。

确定变异后,在迭代前期采用采用DE/best/1/bin变异策略,迭代后期采用DE/rand/1/bin策略,可以让算法在前期更注重于全局搜索,在后期更注重于局部精细化搜索。此外,本文还对学习因子和惯性权重因子也做了改进,由于c1从2.05变到0.5会有比较好的效果,而c2从0.5到2.05会有比较好的效果,惯性权重系数采用自适应公式进行改进。具体参数的改进公式如下:

(7)

式中:c1max和c2max均为2.05,c1min和c2min均为0.5;t为当前迭代次数;tmax为最大迭代次数;ωmax为最大惯性权重因子,本文取0.9,为ωmin最小惯性权重因子,本文取0.5[21-22]。

另外,传统电机代理模型多是面向于结构优化设计,输入变量也多为电机结构参量,基于此参量构建的代理模型虽然可以提高优化设计速度,却无法与系统模型所计算的数据融合。因此,本文以发电机运行特性参量和环境参量作为输入变量构造代理模型,可使构造模型部署至平台与系统耦合,当整个模型启动时,代理降阶模型可根据联合仿真所计算出的PMSG运行参数和实际风场环境参数对目标值进行预测。

2.5 模型集成

虚拟模型与实体设备的交互是实现兆瓦级PMSG完整数字孪生技术框架的重要体现。因此,要求所构建的2 MW PMSG数字孪生虚拟模型具备实时计算、部署方便的特点。在数字孪生建模平台搭建PMSG控制系统及机械部分,可很好的完成发电机设备与风电系统的耦合。将构建的降阶模型利用DT建模平台的联合仿真模型接口进行集成。集成后的降阶模型可通过系统电路输入相关变量来快速计算输出,在保证热模型计算精确度的同时,使计算流程简化提高计算速度。集成后的数字孪生虚拟模型后期可凭借该平台的云关联能力,部署至云平台与实体风机进行交互,通过对数据的融合分析及开发,最终可实现整个风电系统PMSG的数字孪生技术应用。

基于上述研究思路,搭建了基于多模型融合的PMSG数字孪生虚拟模型,图7所示为搭建的2 MW PMSG数字孪生模型结构图。由图可知,在集成后的PMSG数字孪生虚拟模型中,有限元电磁模型作为核心部分,通过不断地计算向系统提供控制信号输入源,机侧外电路根据控制电路输出的信号实现相应控制,并依托机械部分完成PMSG电磁模型的启动。

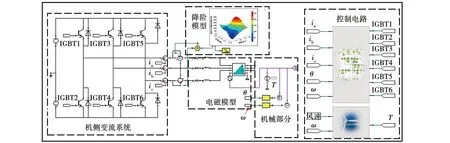
图7 2 MW PMSG结构集成图

3 仿真分析与验证

3.1 电磁模型分析

2 MW PMSG电机几何模型的参数如表1所示。将模型导入Maxwell生成电磁模型,为验证所构建电机电磁模型满足性能及技术要求,通过空载试验及负载试验对电机性能进行分析。此处仅对空载特性进行分析,负载特性基于外电路模型的设置进行分析。

首先,由于PMSG空载状态时,其内部无负载电流,仅有永磁体励磁。因此,对发电机进行空载设置时,应将电枢绕组激励采用电压源方式,电流值不做考虑因而设置为0。空载特性如图8所示。

图8 PMSG空载特性图

图8(a)为电机空载运行的磁力线分布图。由图可知相邻磁极间的磁力线构成磁流通路径,极间出现磁势的最大值与最小值,相邻两个极间之间存在一定程度的漏磁。图8(b)为电机空载反电动势波形图,对反电动势进行谐波分析,还需对其进行傅里叶变换,得到图8(c)的频谱图,可以看到输出电压中存在奇次谐波和偶次谐波,但含量较少,分析原因可知,电机模型在设计时采用了分数槽绕组。空载时齿槽转矩的变化如图8(d)所示,可见平均齿槽转矩为3 700 N·m,与额定转矩相比仅相差0.037,可以很好的减缓电机运行时产生的转矩波动。

3.2 外电路模型分析

为验证所设计电磁模型是否满足预期的技术指标,采用搭建外电路模型的方法模拟额定负载工况。由于机组发电机的启动速度与轴转动惯量大小密切相关,过大的转动惯量会导致PMSG启动缓慢,不利于效果分析。因此,为更好的观察控制电路控制效果,这里将发电机转动惯量设置为2 400 kg·m2。风力机模型叶片半径依据实际运行风电机组参数设置为48 m,空气密度采用标准空气密度1.225 kg/m3,风速设定为额定风速11 m/s。额定负载条件下的发电机特性如图9所示,由图9(a)、图9(b)可知电机转矩在发生振荡后达到额定转矩1 149 kN·m。转速通过控制电路转速环控制,经过短暂超调后达到额定转速17 r/min,并逐渐稳定。额定负载工况下电流波形和输出功率波形如图9(c)、图9(d)所示,电流值为2.5 kA,折合有效值为1.8 kA,输出功率经一段时间的波动后,随着转矩的稳定,随后稳定至2 MW。综上分析可知,所设计的2 MW PMSG数字孪生模型电磁模型符合预期技术指标的要求。但为验证外电路及控制电路是否满足控制要求,还需对不同工况下的运行特性进行进一步的分析。

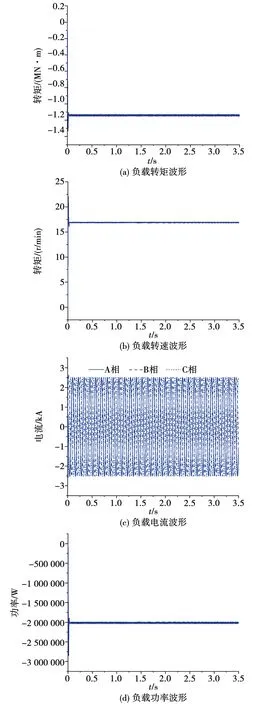
图9 PMSG负载特性图

通过设置11、10、8、6 m/s 4种不同风速工况,对PMSG运行性能进行分析。其中风速变化采用阶梯式变化。不同风速下的PMSG运行特性如图10所示。由图可知,当风速在额定风速11 m/s时,发电机的转速达到17 r/min,转矩、电流、功率也均达到额定状态。当风速向7 m/s逐渐降低时,经过短暂的动态过程,即可达到稳态,控制性能良好。由于转速外环的控制,转速和转矩在稳态时的波动都很小,转速超调也在可接受范围,输出功率各阶段值较符合该等级风机的技术指标,电流值在随着风速变化而降低的同时,幅值也逐渐增大。上述仿真实验结果表明,所设计的外电路及控制电路模型可以实现对PMSG的控制。

图10 不同风速下的PMSG运行特性

3.3 热模型分析与验证

对PMSG在额定风速11 m/s、转速17 r/min的额定运行工况下进行稳态热分析,其中设置环境温度为25 ℃,得到在该运行条件下的PMSG定子温度云图如图11(a)所示。由图可知,定子绕组计算的平均温度为103.21 ℃,定子铁心平均温度为68.446 ℃。由(a)可以看出,定子绕组温度最高,可达到106.19 ℃,其次是定子铁心齿部和轭部,定子端部温度最低。而沿着轴向,温度从电机中部到端部温度定子铁心温度低于定子绕组。定子齿部与绕组间的温差较大,可到达15.74 ℃,这是由于端部与空气间存在热交换。

为验证热模型的有效性与合理性,选取所研究的实体PMSG实际运行SCADA数据作为验证依据,该PMSG运行时以10 min为周期采集的发电机定子绕组温度的平均数据。机组运行时的风速、温度等相关环境参数选取该时段内的风场实际记录数据。基于上述条件对PMSG热模型构造相对应的工况断面,并进行瞬态热计算。计算时通过在场路耦合模型中进行风速设置得到相应的损耗,散热系数根据环境参量计算获得[23]。

分别对9.3、8.2、7 m/s 3种不同风速,同种环境温度运行工况下的热模型进行计算,定子温度云图如图11(b)、图11(c)、图11(d)所示,并对额定运行工况下0、10、20、30、40 ℃ 5种不同环境温度条件下的热模型进行计算。最后,通过与上述运行条件相符的定子绕组温度SCADA数据进行对比分析,对比结果图如图12所示。由图12可以看出实测值与计算值较为近似,经计算相对误差最大为3.4%,最小为1.8%。均未超过5%,经对比分析验证了热模型的有效性与合理性,本文所建热模型能够反映PMSG的定子温升特性。

图12 定子温度实测值与计算值对比图

3.4 基于改进的PSO-SVM降阶模型的分析与验证

为验证改进效果,采用Schwefel函数来进行测试,其函数表达式为

(8)

本文中取d=3;x的范围在[-500,500]。测试结果如图13所示。由图可知,经过信息熵结合差分变异策略优化后的PSO算法的效果明显优于传统PSO算法。

图13 改进效果对比图

支持向量机中的惩罚因子C和核参数g对数据比较敏感,采用改进粒子群算法对SVM进行优化,使模型得到最佳。迭代收敛图如图14所示。由图可知优化效果较好。

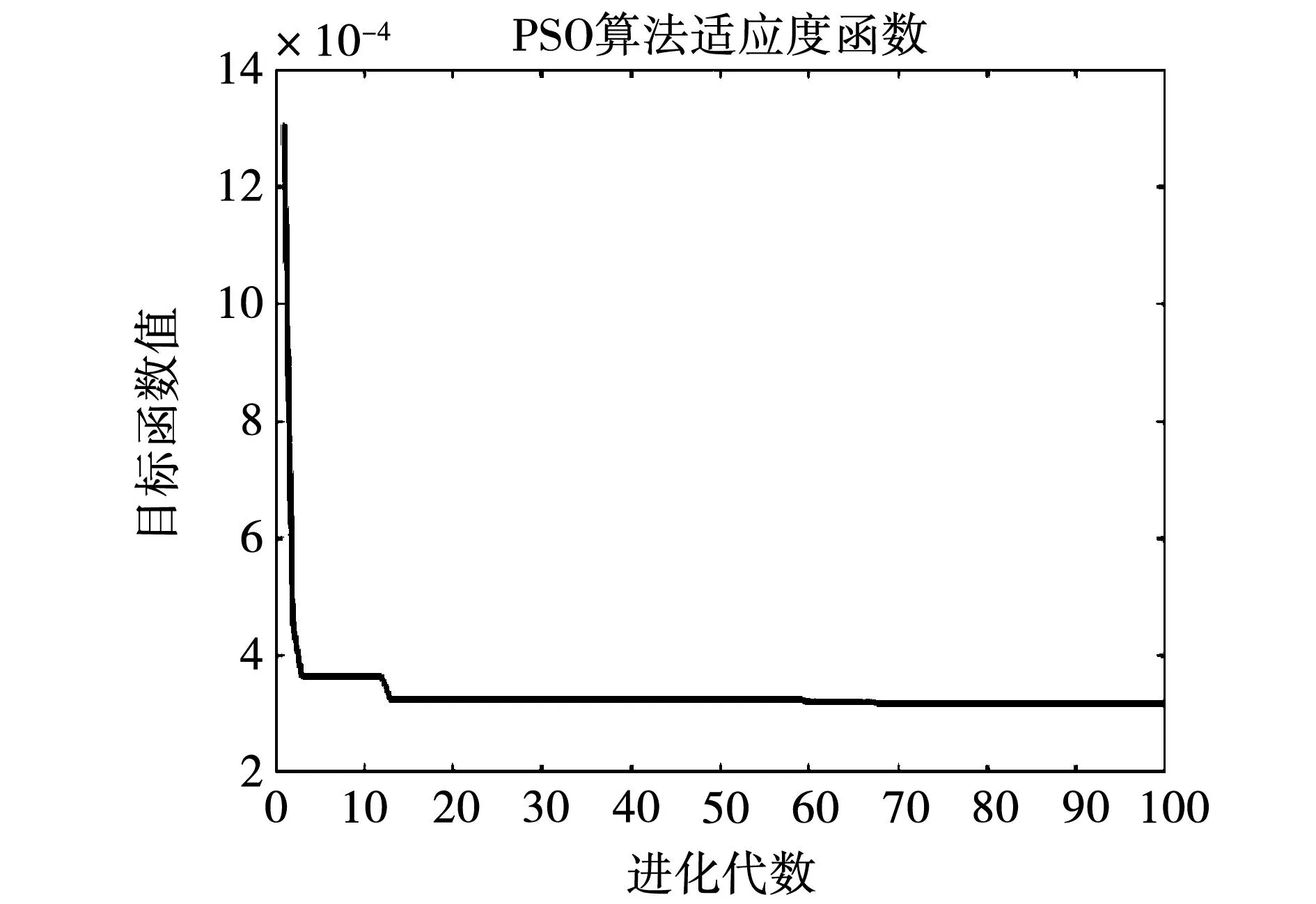
图14 迭代收敛图

定子绕组温度作为衡量PMSG工作状态的关键指标之一,其温升的趋势可以直观地反映设备的运行情况,因此,本文将定子绕组平均温度作为输出变量。考虑后期与风电控制系统集成的影响,本文选取PMSG运行风速与功率作为输入变量。为验证改进PSO-SVM代理模型预测精确度,基于多物理场模型并结合风机实际运行工况参数,进行不同工况下仿真推演,得到89组可以有效反映输入输出关系特性的数据,选取75组作为降阶模型训练数据,14组作为测试数据,对构建的降阶模型进行测试,误差分析方式采用均方误差MSE和方差R2的形式进行判定,MSE越接近于0,R2的值越接近于1.0,表明精确度越高,降阶效果越好[24]。测试结果如图15所示。

图15 预测结果对比图

从图中可以看出,定子绕组平均温度的预测值与热模型计算值非常接近。训练集结果中MSE为0.002 110 1,R2为 0.994;测试集结果中MSE为8.783e-5,R2为 0.999 77。由此可见,建立的降阶模型具有较高的置信度,可替代原有的热模型。

最终,对训练后的降阶模型选择合适的核函数,求解SVM系数,构造相应的回归函数,根据回归函数构造输入与输出关系的响应面。改进PSO-SVM降阶模型的响应面形式如图16所示。

图16 改进的PSO-SVM代理模型响应面形式

3.5 2 MW PMSG数字孪生虚拟模型验证

与实际风机进行有效的数据互联是数字孪生虚拟模型的重要功能,也为后期PMSG数字孪生实现状态监测及维护指导奠定基础。为验证该模型是否具备反映实际PMSG运行情况及完成数据互联的能力,使用技术指标与虚拟模型相一致的实体2 MW直驱风机SCADA运行数据进行互联,该数据记录周期为5 s,即一个SCADA数据表示机组状态参数在5 s内的平均值,由于发电机组传感器采集技术及安装技术的限制,仅能获取反映发电机部分特性的运行数据。因此,本文以PMSG的转速与输出功率为监测量,选取10个不同风速条件下的转速值及功率值与虚拟模型计算值进行对比,为有效避免无效数据对验证结果的影响,对所选取数据通过核密度估计法进行预处理[25]。通过计算可获得虚拟模型转速与输出功率值,与SCADA数据对比误差结果如图17所示。可以看出计算值与实测功率值较为接近,功率正负误差范围不超过100 kW。转速正负误差范围不超过0.3 r/min。功率与转速最大误差分别为4.6%、4.8%,最小误差分别为1.2%、0.32%,平均误差率小于5%,结果表明所设计的虚拟模型可以初步满足数字孪生技术关于虚拟模型部分与实体设备运行数据互联的要求。但是真实的风电系统运行特性具有随机性,数据以周期平均值形式进行描述,所构建的数字孪生虚拟模型在构建过程存在一定简化处理,另外模型的几何参数及物理特性相关参量与实体风电系统PMSG并不完全一致。因此,对于图中处于不同风速运行工况下的PMSG虚拟模型计算值与实际运行数据稍有差异。

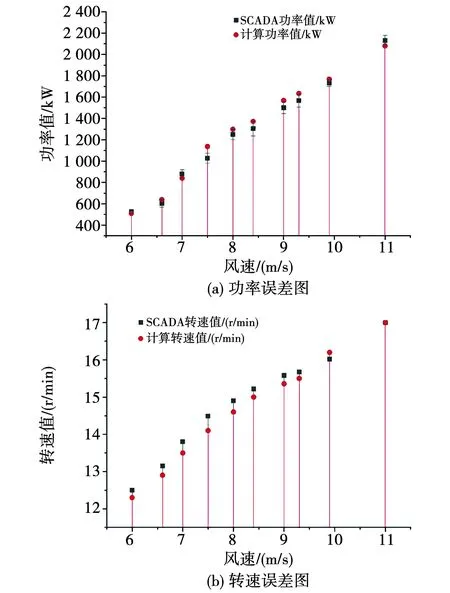
图17 误差分析图

此外,为了验证集成后的降阶模型的精确性,随机抽取14个热模型计算数据作为样本。将降阶模型集成至DT建模平台,根据选取样本的进行相关参数的设置,并进行计算。将样本值与降阶模型计算值进行误差分析。误差分析结果如图18所示。由图可知,定子绕组平均温度的预测值与热模型计算值非常接近,误差最大仅为1.4%,表明集成后的降阶模型符合在保持精确度的同时,满足简化模型提高计算效率的要求。

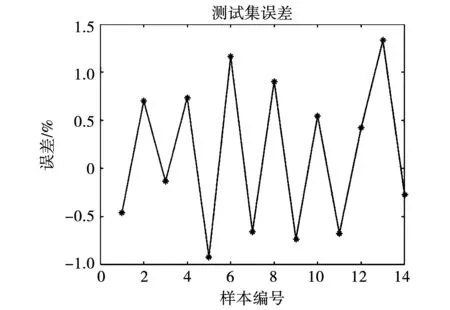
图18 误差分析图

4 结 论

以2MW PMSG为研究对象,采用DT技术建模方法,对发电机电磁模型、外电路及控制电路模型、热模型及代理模型进行设计,从而完成整个DT虚拟模型的构建。通过仿真分析测试验证得到以下结论:

1)设计发电机电磁模型,利用数字孪生建模平台进行外电路搭建,并与控制电路进行联合仿真,通过模拟不同工况进行分析。结果表明,所设计的电磁模型符合相关技术指标,构建的外电路及控制模型可实现系统耦合的要求。

2)建立热模型,并进行瞬态热分析。与SCADA数据对比可知,误差在可接受范围内。引入信息熵与差分变异策略相结合的方法改进PSO-SVM代理模型技术,使代理模型能够解决PSO在后期迭代中种群多样性迅速降低,从而搜索不到全局最优解的缺陷,提高对SVM的优化效果,从而对热模型进行降阶,通过误差分析验证了降阶模型的准确性。

3)将集成后的2 MW PMSG数字孪生虚拟模型进行分析计算。采用SCADA数据与计算结果进行比对可知,平均误差不超过5%。结果表明虚拟模型可以有效的反映PMSG的运行特性。

该模型的建立为后期通过云平台部署及实现完整的风电机组DT技术的应用打下坚实基础。