边界条件含特征参数的三阶微分算子的自伴性和特征值的依赖性
林秋红, 钱志祥
(广东理工学院 基础课教学研究部, 广东 肇庆 526100)
众所周知,机械振动、电路、声学散射等物理上的问题,都涉及到求解微分算子的边值问题[1-4].微分算子的边值问题是微分算子理论的一个重要部分,特别是微分算子特征值的扰动问题,近年来引起了广大学者的关注,并出现了许多有意义的研究成果.其中关于偶数阶微分算子的情形,已经有了比较完善的结论[5-14].然而,关于奇数阶微分算子的边值问题,研究成果却很少.近年来,Ugurlu[15]研究了一类三阶微分算子分别在分离,实耦合和复耦合边界条件下所产生的边值问题,通过证明问题生成的微分算子是自伴算子得到特征值是实数,进一步研究了特征值关于问题的连续依赖和可微依赖性,得到了相应的微分表达式.同年,Ugurlu[16]考虑了具有转移条件的情形并得到了类似的结论.在文献[15]的基础上,2020年,Li等[17]研究了边界条件带有谱参数的三阶微分算子的自伴性以及格林函数,2022年,Bai等[18]进一步考虑了这类三阶微分算子的特征值关于给定参数的连续性和可微依赖性.同年,孙康等[19]考虑了一类边界条件含谱参数且具有转移条件的三阶微分算子,运用类似的方法证明了算子的自伴性.
在文献[15-18]的基础上,本文考虑一类具有转移条件且边界条件带有特征参数的三阶微分算子的自伴性及特征值的连续性和可微性.通过构造相应的Hilbert空间和线性算子T,运用算子理论证明了问题生成的线性算子T是自伴算子,进一步得到问题的特征值是实数,在这个基础上,考虑了特征值和特征函数的连续性,研究了特征值关于边值问题参数的可微性,并得到了相应的微分表达式.
1 预备知识
考虑如下三阶对称微分方程:
(1)
两端具有特征参数的分离型边界条件:
转移条件:
式中:-∞ q0,q1,p0,p1,w∈Lloc(J,R),q0>0,w>0 参数αk,βk(k=1,2,3,4)及d1,d2是任意的实数,并且满足: (8) 定义y的拟导数如下[20]: (9) (10) 式中 Lmaxy=l(y)y∈Hw 最大算子域为 对任意的y,z∈Dmax,通过分部积分可得Largrange恒等式 (11) 式中 (12) 通过拟导数的定义,可将微分方程(1)转化为以下一阶系统 Y′+QY=λWYx∈J (13) 令直和空间H=Hw⊕C⊕C,对任意F=(y(x),h1,h2)T,G=(z(x),k1,k2)T∈H,hi,ki(i=1,2)均为复数,在空间H中定义内积如下: (14) 式中:ρ1=1/τ1,ρ2=1/τ2. 显然H是一个Hilbert空间.定义算子T如下: 式中 (15) 为了简便,令 (16) 即 因此,可通过在H中讨论微分算子方程TF=λF研究边值问题(1~7). 由以上算子T的定义,显然有如下结论. 引理1边值问题(1~7)的特征值与T的特征值相同,特征函数是算子T相应特征函数的第一个分量. 引理2算子T的定义域D(T)在H中是稠密的. 证明这与文献[19]定理2.1的证明过程类似,因此省略. 定理1线性算子T是对称的. 证明设任意的F=(y(x),M1(y),M2(y))T,G=(z(x),M1(z),M2(z))T∈D(T),由式(10,11)可得 (17) 由边界条件、转移条件,式(12,16)可得 由式(12)和式(17,21)得〈TF,G〉-〈F,TG〉=0,因此算子T是对称的. 定理2线性算子T是自伴的. 证明由于算子T是对称的,要证明T在H中是自伴的,只需证明:若对任意的F=(y(x),M1(y),M2(y))T∈D(T),有〈TF,G〉=〈F,U〉成立,则G∈D(T),且TG=U.其中G=(z(x),m1,m2)T,U=(u(x),n1,n2)T,即 1)z(x),z[1](x),z[2](x)∈ACloc(J),l(z)∈Hw; 2)m1=M1(z)=α1z(a)-α3z[2](a),m2=M2(z)=d1β1z(b)+d2β3z[2](b); 3)Liz=0(i=3,4,5,6); 4)u(x)=l(z); 5)n1=N1(z)=-α2z(a)+α4z[2](a),n2=N2(z)=-d1β2z(b)-d2β4z[2](b). 下面证明1)~5)成立. 即 〈l(y),z〉w=〈y,u〉w 由经典算子理论[21]可得,z(x)∈D(T),故1)成立. 因为算子T是对称的,所以有〈TF,G〉=〈F,TG〉,再由上述F的取法可得 〈l(y),z〉w=〈y,l(z)〉w,结合〈l(y),z〉w=〈y,u〉w,得到〈y,l(z)〉w=〈y,u〉w,即l(z)=u.故4)成立. 再由4)可知,对任意的F∈D(T),〈TF,G〉=〈F,U〉,又〈TF,G〉=〈F,TG〉,故有 于是,有 结合式(11)可得 (22) 为了方便,下面记 由Naimark Patching Lemma[22]可知,存在(y1(x),y11,y12)∈D(T),使得 Y1(b)=Y1(c-)=Y1(c+)=0 代入式(22)可得m1=α1z(a)-α3z[2](a). 类似的,存在(y2(x),y21,y22)∈D(T),使得 Y2(a)=Y2(c-)=Y2(c+)=0 代入式(22)可得 m2=d1β1z(b)+d2β3z[2](b) 所以2)成立.利用同样的方法,可证5)成立. 下面证3)成立.选取(y3(x),y31,y32)∈D(T),使得 代入式(22)可得L3z=0.用同样的方法,可以得到L4z=L5z=L6z=0.则3)成立. 综上所述,线性算子T在H中是自伴的. 由算子T的自伴性,可得下面推论. 推论1算子T的特征值是实的,并且没有有限的聚点. 推论2设λ1和λ2是算子T的两个不同的特征值,(u1(x),u11,u12)和(u2(x),u21,u22)分别为其对应的特征函数,则u1(x)和u2(x)在下述意义下是正交的: 首先根据常微分理论中解的存在唯一性定理[17]给出边值问题(1~7)特征值存在的充分必要条件. 为了方便,将边界条件(2~4)写成矩阵形式,即 式中 下面给出特征值所满足的判别函数. 设φ11(x,λ),φ12(x,λ),φ13(x,λ)是微分方程(1)在区间[a,c)满足初始条件: 的线性无关的基本解组,其中E是三阶单位矩阵.它的Wronski行列式与变量x无关,且是关于特征参数λ的整函数,记为W1(λ),则 设φ21(x,λ),φ22(x,λ),φ23(x,λ)是微分方程(1)在区间(c,b]满足初始条件(5~7)的线性无关解,它的Wronski行列式与变量x无关,且是关于特征参数λ的整函数. 其中ci∈C(i=1,2,…,6).若u(x,λ)满足转移条件,则c1=c4,c2=c5,c3=c6. 现在区间J=[a,c)∪(c,b]上定义函数 其中 x∈[a,c) x∈(c,b] 这里Φ1(c,λ)=Φ(c-,λ),Φ2(c,λ)=Φ(c+,λ).对任意的x∈J,Φ(x,λ)是关于λ的整函数. 引理4一个复数λ是算子T的特征值当且仅当λ满足Δ(λ)=det(Aλ+BλΦ(b,λ))=0.称Δ(λ)=det(Aλ+BλΦ(b,λ))为判别函数. 证明结合引理3,通过与文献[19]定理3.1的类似证明,可得结论成立. 下面引入Bananch空间及相应的范数. X=L(J)×L(J)×L(J)×R5×M2×2(R)×M2×2(R) 对任意的ω=(p0,p1,ω,θ,a,b,c-,c+,A,B)∈Ω⊂X,在空间X的范数定义为 其中 引理5设ζ∈J=[a,c)∪(c,b],y=y(·,ζ,c0,c1,c2,p0,p1,p2,w)是微分方程(1)和(13)满足条件y[j](ζ,λ)=cj(j=0,1,2.)的解,则该解对其所有的变量都连续. 证明由一阶系统(13)和文献[23]定理 2.7可得结论. 定理3设λ=λ(ω)是算子T的特征值,对ω0=(p00,p10,w0,θ0,a0,b0,c0-,c0+,A0,B0),有λ=λ(ω)在ω0处连续.即对任意的ε>0,存在δ>0,使得对任意的ω∈Ω,当 ‖ω-ω0‖= |θ-θ0|+|a-a0|+|b-b0|+|(c-)- (c0-)|+|(c+)-(c0+)|+ ‖A-A0‖+‖B-B0‖<δ 有|λ(ω)-λ(ω0)|<ε. 证明这与文献[18 ]定理3.2的证明过程类似,因此省略. 引理6设ω0=(p00,p10,w0,θ0,a0,b0,c0-,c0+,A0,B0)∈Ω,λ=λ(ω)是算子T的一个特征值.若λ(ω0)是单重特征值,则在Ω中存在ω0的某邻域U(ω0),满足对∀ω∈U(ω0),λ(ω)是单重特征值. 证明若λ(ω0)是单重特征值,则Δ′(λ(w0))≠0.因为Δ(λ)是λ的整函数,由定理3可知结论成立. 定义1设u(x)满足边值问题(1~7),u1=M1(u),u2=M2(u)且有 成立,则称(u(x),u1,u2)T为规范化特征函数. 定理4设λ=λ(ω)(ω∈Ω)是Ω内ω0的某个邻域内所有ω的n(n=1,2,3)重特征值.若 (uk(x,ω0),uk1(ω0),uk2(ω0))∈H(k=1,2,3) 证明首先证明λ=λ(ω)(ω∈Ω)是算子T的单重特征值时结论成立. 设λ=λ(ω0)是算子T的单重特征值,(y(x,ω0),y1(ω0),y2(ω0))∈H是其对应的特征函数,且满足: 由引理6知,存在ω0的邻域M,满足对∀ω∈M,λ(ω)是单重特征值.由定理3知: 当ω→ω0时,λ(ω)→λ(ω0)成立. 令边界矩阵(Aλ,Bλ)3×6(ω)=(Aλ(ω),Bλ(ω))3×6,则当ω→ω0时,(Aλ,Bλ)3×6(ω)=(Aλ,Bλ)3×6(ω0).由文献[5]中定理3.2可知,当ω→ω0时,存在特征值λ(ω)对应的特征函数(y(x,ω),y1(ω),y2(ω))∈H,使其第一个分量y(x,ω)在区间J上满足: (23) 再由式(15,16)可得,当ω→ω0时, y1(x,ω)→y1(x,ω0),y2(x,ω)→y2(x,ω0) (24) 下面令λ(ω0)对应的规范化特征函数(u(x,ω0),u1(ω0),u2(ω0))T及第一个分量的拟导数u[k](x,ω0)(k=1,2)分别为 类似的,令λ(ω)对应的规范化特征函数(u(x,ω),u1(ω),u2(ω))T及第一个分量的拟导数u[k](x,ω)(k=1,2)形式分别为 由式(23,24)知结论成立. 设特征值λ(ω)关于ω0的某一邻域内所有ω的重数为n(n=2,3).由定理3和文献[6]中定理3.5可知,当ω→ω0,存在n个线性无关的特征函数 (yk(x,ω),yk1(ω),yk2(ω))∈Hk=1,…,n 使其第一个分量yk(x,ω)在区间J上满足: 通过类似上面的讨论可得定理的结论. 定义2[6]设Γ是Banach空间X到Banach空间Y上的映射,若存在有界线性算子dΓx:X→Y,对h∈X,当h→0时,有 |Γ(x+h)-Γ(x)-dΓ(h)|=ο(h) 则称映射Γ在点x处是Fréchet可微的. 引理7[6]假设函数f∈Lloc(J),则 定理5设ω=(p0,p1,w,θ,a,b,c-,c+,A,B)∈Ω,λ=λ(ω)是算子T的特征值,(y(x,ω),y1(ω),y2(ω))∈H是其对应的规范化的特征函数.E为单位矩阵,S为2×2实数矩阵.若λ(ω)在ω的某一邻域内的几何重数不变,则λ关于方程系数函数p0,p1,权函数w,边界条件参数θ和特征参数依赖的边界条件矩阵A、B都是可微的且导数公式如下: 1) 固定ω中除p0之外的所有变量,令λ=λ(p0)为特征值,则λ是Fréchet可微的且有 h∈L(J) 2) 固定ω中除p1之外的所有变量,令λ=λ(p1)为特征值,则λ是Fréchet可微的且有 h∈L(J) 3) 固定ω中除w之外的所有变量,令λ=λ(ω)为特征值,则λ是Fréchet可微的且有 h∈L(J) 4) 固定ω中除θ之外的所有变量,令λ=λ(θ)为特征值,则λ是Fréchet可微的,有 5) 固定ω中除边界条件参数矩阵A之外的所有变量,令λ=λ(A)为特征值,且det(A+S)=-τ1,则λ是Fréchet可微的且有 6) 固定ω中除边界条件参数矩阵B之外的所有变量,令λ=λ(B)为特征值,且det(B+S)=-τ2,则λ是Fréchet可微的且有 证明为了方便,对于给定的参数γ,令λ=λ(γ)和λ=λ(γ+h)所对应的规范化特征函数分别为 (25) 式中 (26) 1) 固定ω中除p0之外的所有变量,令λ=λ(p0)和λ=λ(p0+h)所对应的规范化特征函数分别为F(p0)和G(p0),F(p0)和G(p0)具体如式(25,26). 由空间H上内积定义可得 由式(1)和分部积分法,可得 (27) (28) (29) (30) 由式(18,19,27~30)可得 (31) 由拟导数的定义(9)可知: 把式(32)和(33)代入式(31),可得 因此,1)成立. 2) 固定ω中除p1之外的所有变量,令λ=λ(p1)和λ=λ(p1+h)所对应的规范化特征函数分别为F(p1)和G(p1),类似1)的方法,由分部积分法可得 因此,2)成立. 3) 固定ω中除w之外的所有变量,令λ=λ(w)和λ=λ(w+h)所对应的规范化特征函数分别为F(w)和G(w),F(w)和G(w)具体如式(25,26),则有 由式(1,25,26)可知: i[q1z′+(q1z)′]+p1z} i[q1y′+(q1y)′]+p1y} 因此有 (34) 由式(18~21,34)可得 因此3)成立. 4)~6)与文献[18]定理4.1证明过程类似,因此省略. 定理6设ω=(p0,p1,ω,θ,a,b,c-,c+,A,B)∈Ω,λ=λ(ω)是算子T的特征值,(y(x,ω),y1(ω),y2(ω))∈H是其对应的规范化的特征函数.若λ(ω)在ω的某一邻域内的几何重数不变,则λ关于内部不连续点c左右两侧c1,c2和边界点a,b是可微的且导数公式如下: 1) 固定ω中除c1之外的所有变量,令λ=λ(c1)为特征值,则λ是Fréchet可微的且有 λ′(c1)=Y*(c1)KY′(c1) 2) 固定ω中除c2之外的所有变量,令λ=λ(c2)为特征值,则λ是Fréchet可微的且有 λ′(c2)=-d1d2Y*(c2)KY′(c2) 3) 固定ω中除a之外的所有变量,令λ=λ(a)为特征值,则λ是Fréchet可微的且有 λ′(a)=-Y*(a)KY′(a) 4) 固定ω中除b之外的所有变量,令λ=λ(b)为特征值,则λ是Fréchet可微的且有 λ′(b)=d1d2Y*(b)KY′(b) 证明1) 固定ω中除c1之外的所有变量,令λ=λ(c1)和λ=λ(c1+h)所对应的规范化特征函数分别为F(c1)和G(c1),F(c1)和G(c1)具体如式(25,26),则有 (35) 注意到当h→0时, 由引理7可知: 所以对式(35)两边同时除以h,并取极限h→0,得 因此1)成立. 2) 固定ω中除b之外的所有变量,令λ=λ(b)和λ=λ(b+h)所对应的规范化特征函数分别为F(b)和G(b),F(b)和G(b)具体如式(25)和(26),则有 (36) 注意到当h→0时,有 由引理7可知: 因此对式(36)两边同时除以h,并取极限h→0,得 因此4)成立. 2),3)的证明同1),4)类似.

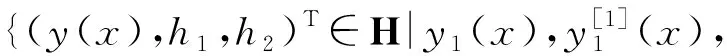
2 算子T的自伴性
3 特征值和特征函数的连续性
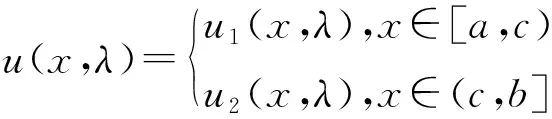




4 特征值的可微性





