配电网中电压不平衡治理设备的优化配置方法

何 峰, 魏光明, 尹巧荣, 倪源宏, 王 杰

(国网甘肃省电力公司兰州供电公司, 甘肃 兰州 730050)

随着光伏渗透率的不断提高,配电网的电能质量受到了极大挑战,尤其以公共连接点的电压不平衡现象表现最为突出,电压不平衡会造成系统中线路损耗过大、设备发热增加,影响配电网的安全稳定运行.

对于配电网中三相电压不平衡的治理,主要采用换相技术对负荷调整尽量使其对称化[1-2],但该方法对配电网中分布式负荷控制较弱且需要断电操作.此外还有采用相间电容[3]和调节分布式电源电压负序分量[4]的方法,但该方法不能连续平滑调节,补偿能力有限,且影响到母线的电能质量.康勇等[5]提出了一种采用SVG对电网提供无功功率补偿的方法以达到治理目的.翟灏等[6]采取单台SVG对7节点系统进行电压不平衡现象治理,并根据非线性规划原理和集合辅助分析对模型求解,但面临复杂网络时,只采取单台补偿措施显然难以达到治理效果最优.包正楷等[7]对电网运行场景进行分区,提出了不同电压跌落程度下的SVG和新能源无功协调补偿策略,实现了既定控制目标.Zhao等[8]提出利用储能系统具有移峰能力和充放电响应速度快的特点与SVG配合使用,建立双层协同规划模型,上下层分别采用自适应交叉率和变异率的精英保留策略遗传算法和二次规划算法求解以实现优化配置.Sun等[9]将损耗最小和利润最大作为目标函数从而建立SVG优化模型,采用主从分裂法通过对PCC处的电压和功率交互作用进行求解.Wang等[10]提出一种含SVG的多装置分散最优电压调节方法,并通过双层博弈竞价过程解决了这一问题.

上述文献多采用SVG和其他补偿策略配合使用对电压不平衡现象治理,但未考虑到设备所接入系统中的具体位置对电压不平衡的影响程度.本文提出了一种基于电压灵敏度法矩阵和Gamultiobj函数的电压不平衡治理设备优化配置方法.引入电压灵敏度矩阵法求解电压薄弱节点作为接入位置集合,根据治理需要建立目标函数和约束条件模型,并通过引入权重和惩罚因子建立动态模型以保证解集的准确性,利用小生境技术对Gamultiobj函数遗传算法[11]的子种群适应度进行改进,最后通过仿真验证本文方法的可行性和有效性.

1 基于电压灵敏度矩阵的电压薄弱节点求解方法

对于系统第k条线路而言,其首末端电压差可以表示为

(1)

其中:P和Q分别为流经此线路的有功和无功功率;R和X分别为此线路的电阻和电抗值.

在改变分布式电源的注入功率P和Q时,此线路的电压降增量可表示为

(2)

由此可得此段线路末端对应的第k个节点电压的变化量为

(3)

其中:i为节点编号.则节点k电压对有功功率注入的灵敏度为

(4)

对无功功率注入的灵敏度为

(5)

将道路关联矩阵T[12]引入到式(1)中,得到第k-1个节点的电压为

(6)

化简可得

(7)

其中:U为除平衡节点外所有节点的电压幅值向量;E为n×1阶的全1矩阵;∘为Hadamard乘积,对应Matlab软件中的点乘;·为叉乘.

式(7)求导后的表达式可衡量任意节点间无功功率变化对于某节点电压的影响,即为

(8)

整理可得电压-无功灵敏度矩阵为

(9)

当网络拓扑结构和阻抗参数确定后,根据式(9)即可得到网络的电压-无功功率灵敏度矩阵.矩阵中的数值绝对值越大,代表此节点的电压越容易受到波动.

2 SVG多目标优化配置的模型

2.1 目标函数

三相电压不平衡度计算公式依据GB/T 15543-2008《电能质量 三相电压不平衡》标准规定:

(10)

其中:U1、U2为正序、负序电压值.

在配电网中,还需要考虑SVG接入的经济性.故需计及装置配置的经济性指标f2:

(11)

式中:S为节点i处SVG的固定投资成本;Qi为接入SVG的数量;CSVG为SVG正常或故障时的维护费用;DSVG为SVG的折旧费用;m≤n.

潮流等式约束:

(12)

其中:PGj、PLi表示发电机和负荷注入的有功功率;QGi、QLi表示发电机和负荷注入的无功功率;QSVG_i表示节点i最终的无功补偿容量;Ui、Uj表示对应节点的电压幅值;Gij、Bij表示系统导纳矩阵的实部和虚部;θij表示两节点之间的电压相角差.

不等式约束:

(13)

其中:Uimin、Uimax为电压幅值约束;PGimin、PGimax为发电机有功功率约束;QGimin、QGimax为发电机无功功率约束;PPVmax为光伏电源最大功率约束;QSVG_imin、QSVG_imax为SVG接入容量约束.

2.2 引入惩罚因子的自适应权重动态优化模型

多目标优化方法中的目标函数实际上是相互矛盾和制约的,所以本文针对目标函数和约束条件,分别加以改进,以满足优化需要.

针对固定权重的分配方式所带来的难以识别场景,引入权重因子α将两个目标函数合并建立总目标函数F使其最小:

其中:β1、β2为相应线性关系系数,满足β1、β2≥0.当f1越大时,与之相关联的α也要随之增大,代表此时不平衡度已逐渐扩大,所以经济性指标f2的权重(1-α)需要减小,以弱化网络运行成本.

在多目标函数求解过程中,不等式约束条件是保证系统稳定运行的关键因素.求解过程中所得到的解不一定时刻满足约束条件,所以需要引入惩罚因子对约束条件做进一步的限制[13].

将式(13)改为罚函数:

其中:Ti为式(13)中的Ui、PGi、QGi、PPV、QSVG_i.故对不等式约束条件的改进为

G=ωigTi

(18)

其中:ωi为惩罚因子,一般最初值设为0.01.

3 基于遗传算法的Gamultiobj函数求解

包含Gamultiobj函数的遗传算法为多目标优化问题提供了良好的解决方法.该函数中定义了初始种群信息,通过不断判别种群适应度对遗传算法进行重构,优化了种群.

3.1 帕累托前沿

多目标问题的遗传算法可在1次求解过程中就获得近似帕累托最优解集,其优点在于将子目标函数值的基因表达进行简单连接,使其相互独立参与算法进化过程.

通过引入协同进化概念,将整个搜索空间分化为众多子区间,而应用于这些子区间的各个子种群便在进化过程中相互合作和竞争,从而形成帕累托前沿.在多目标函数优化过程中,当满足x*∈R时,使得fi(x)≤fi(x*)(i=1,2,…,k)中至少有一项成立,则x*为多目标求解问题中的一个可行解[14],故帕累托最优解集为

Z={p=f(x*)|x*∈P}

(19)

而单目标函数的最优帕累托解集为帕累托前沿,其表达式为

P={x*∈R|∅x∈R,f(x)≤f(x*)}

(20)

3.2 帕累托求解

对下一代种群的进化是多目标函数Gamultiobj在优化过程中的核心步骤,因此种群进化的取值对算法是否保持最优性起到了重要作用.为了解决算法中出现的漂移现象[15],采用能够修复子种群环境适应度的小生境技术[16],这是一种基于共享机制所衍生的算法,其目的是保证帕累托解集的最优性:

其中:h(i)为修复过程之前个体的适应度值;Ai为当前个体i在群体中的共享度比例;ha(i)为修复过程之后个体的适应度值;A(L)为共享函数,它反映出个体之间的距离L是负相关关系;Lij为个体i和j之间的欧氏距离;ζ为小生境半径,可用帕累托最优解集中所有个体之间的期望间距最小值来确定.

图1为Gamultiobj函数结构流程图.

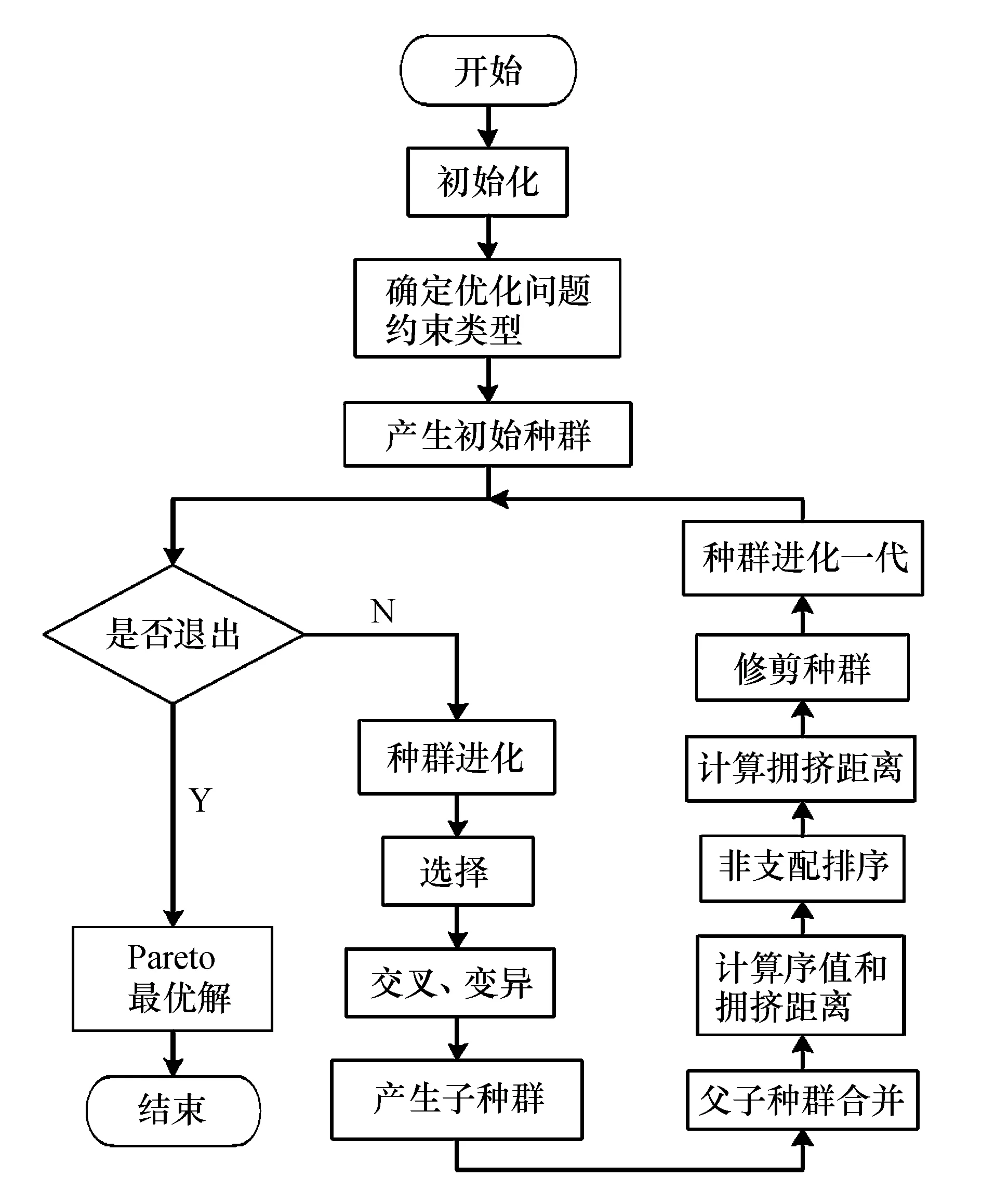
图1 Gamultiobj函数求解流程图Fig.1 Gamultiobj function solution flow chart

4 算例分析

本文选取了IEEE30节点系统,如图2所示.系统的基准容量为10 MV·A,光伏逆变器标称功率500 kW,逆变器直流侧电压为500 V,交流输出270 V,通过变比0.27/10的升压变压器接入到10 kV配电网.将单机容量为1 MW的光伏电站接入到节点5、8、9、13中,进行仿真实验.

图2 IEEE30系统节点图Fig.2 IEEE30 System node diagram

图3 节点电压灵敏度数值图Fig.3 Numerical diagram of node voltage sensitivity

4.1 电压灵敏度矩阵法对节点电压的分析

根据第1节内容所述,求得IEEE30系统中各电压节点灵敏度数值如图3所示.灵敏度数值绝对值越大代表节点越薄弱,在这些节点施加装置可以取得较好的效果.根据图3可以看出,节点6、10、18、26的数值绝对值最大,分别为:0.101、0.113、0.110、0.103.故在后续模型求解过程中,以此4个节点为节点备选集合,进行实验分析.

4.2 SVG优化配置方法的帕累托解集和不同方案对比

将前文所述所求得的帕累托解集投影至二维平面,则距离原点最近的点是以电压不平衡度和经济性为目标函数所求取的最优解,结果如表1所列.

表1 SVG接入节点方案

为了进一步验证考虑经济性下的SVG装置接入配电网后对电压不平衡度治理效果,采用不同节点组合的方式进行实验.在备选节点集合中通过更换接入节点,对比不同情况下的电压不平衡度.其中,在约束条件下的帕累托最优解如表2所列,电压不平衡度的对比如图4所示.

表2 约束条件下的帕累托最优解

图4 SVG不同接入节点方案下的电压不平衡度对比Fig.4 Comparison of voltage unbalance in SVG with different access node solutions

根据表1和图4可知,以方案1、4为一组,方案2、3为一组,综合对比可知,多投入一台SVG设备,会使电压不平衡度大为下降,治理效果更加优异;对比方案1、4可知,方案1的治理效果将稍优于方案4,这是因为方案1中将SVG接入到了电压最薄弱节点中,造成电压不平衡度显著下降并维持较低水平,且根据表2此方案的经济成本最低,符合多目标优化模型和算法的要求.因此,最优接入的方案为:节点6、节点10和节点18.

5 结论

针对配电网中高比例光伏发电系统导致的电压不平衡问题,提出了一种基于电压灵敏度矩阵法和Gamultiobj函数遗传算法的电压不平衡治理设备优化配置方法.仿真实验结果表明,在多目标算法中通过小生境技术以解决遗传算法中出现的漂移现象,可得到帕累托最优解集.通过4种方案对比不同治理措施下的电压不平衡度和经济性指标,结果表明在电压最薄弱节点中接入SVG装置可有效抑制电压不平衡,仿真结果验证了本文方法的有效性.

致谢:本文得到国网甘肃省电力公司科技项目(SGGSLZ00FCJS2000712)的资助,在此表示感谢.