思维导图与波利亚解题思想融合的教学实践研究
霍云

摘要:二次函数是初中数学知识体系的重要构成.在新的教育生态下,如何整合现代教育技术与数学解题思想,引导学生学会思考、学会解题,是当前培养和发展初中学生数学解题能力的应有之举.以波利亚解题思想作为理论支撑,以“二次函数”教学实践为载体,活用思维导图,探索优化数学解题过程、提高学生数学解题能力的实践路径.
关键词:思维导图;波利亚解题思想;初中数学;二次函数
数学解题的思维过程是学生迁移运用数学思想、感知数学本质的过程.在新课程改革持续推进的背景下,数学教育工作者如何在传授知识的基础上,促使学生学会思考、学会解题,是数学教学顺应新课程改革、提高教学质效、培养和发展学生核心素养的应有之义.波利亚的数学解题思想则为提高学生解题能力、教会学生思考提供了理论支撑.波利亚的解题思想具体地体现在《怎样解题》一书中,他将解题过程分为“理解问题、拟定计划、执行计划、检验回顾”四个步骤.思维导图作为一种现代教育形式,可以将抽象的数学知识具体化,从而帮助学生理解问题、明晰解题思路.本文中以“二次函数”教学为例,探索思维导图与波利亚解题思想的有机融合,提高学生问题解决能力.
1 以图示意,理解问题
理解问题是解决问题的前提.在理解问题的过程中,教师应引导学生找出题目蕴含的未知和已知信息,分析已知量与未知量的关系,帮助学生明确问题的本质、求解的条件和目标.在此环节,教师可以引导学生通过题目中的已知条件,整合已有知识经验,绘制思维导图,以图示意,在梳理题目信息的过程中找到解题的关键信息.
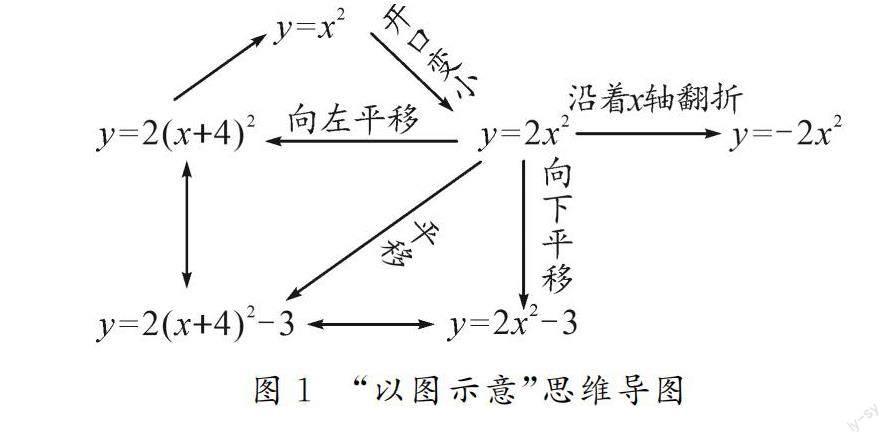
例1 根据“上加下减、左加右减”的图象平移规律,分别画出函数y=x2,y=2x2,y=-2x2,y=2x2-3,y=2(x+4)2,y=2(x+4)2-3的图象.
师:以一般式y=ax2+bx+c(a≠0,a,b,c为常数)为例,其中的系数a,b,c分别有什么作用?
生1:a的正负决定抛物线的开口方向.
生2:a与b决定对称轴的位置.
生3:c决定抛物线与 y 轴的交点坐标.
师:y=a(x-h)2+k(a≠0)是二次函数的什么形式?h和k的意义分别是什么?
生:顶点式.h和k分别是抛物线顶点的横坐标和纵坐标.
师:顶点式和一般式可以相互转化吗?如果可以,顶点式中的h和k与一般式中的系数a,b,c之间是否存在关系?存在怎样的关系?
生:顶点式和一般式可以相互转化.h=-b/2a,k=4ac-b2/4a.
在师生的对话交流中,带领学生复习和梳理关于二次函数图象的知识点,从而形成如图1所示的思维导图.
2 按图索旨,拟定计划
拟定计划是解决问题的关键,同时也是发展学生数学思维、引导学生形成解题思路的重要过程.波利亚解题思想认为在拟定计划阶段,解题者在理解问题的基础上,应对要解决的问题进行模式识别,熟练运用已有的解题经验和掌握的数学思想方法,在知识迁移运用的基础上,产生题目的解决方案.按图索旨,让学生通过思维导图重构自身的知识结构,将零散的知识信息变为系统化的知识体系,使学生在面对问题时,可以快速在脑海中找到解决问题所需要的知识.
例2 将抛物线y=(x-3)2-4沿着直线y=2x-10的方向平移,平移后的抛物线经过点M(0,10),则平移后得到的抛物线的解析式是什么?
分析:例2是例1的延伸,学生面对此问题时,会在已有经验中搜索关于此类问题的解题方法,根据“上加下减,左加右减”的平移规律,形成如图2所示的思维导图.同时,在数学建模思想的作用下,设平移后的抛物线解析式为y=(x+h)2+k,根据二次函数顶点式的性质得出平移前的抛物线y=(x-3)2-4的顶点为(3,-4),且点(3,-4)在直线y=2x-10上,由此推断出平移后的抛物线的顶点坐标(-h,k)也在该直线上,将(-h,k)代入y=2x-10中,得k=-2h-10,又10=(0+h)2+k,很容易就会求出h和k的值,从而得到平移后的抛物线解析式.
3 以图梳理,执行计划
执行计划是学生将解题思路具体化的阶段,也是锻炼学生数学运算能力、养成良好答题习惯的重要过程.解题者可以通过思维导图梳理解题思路,使解题过程的书写逻辑性更强.
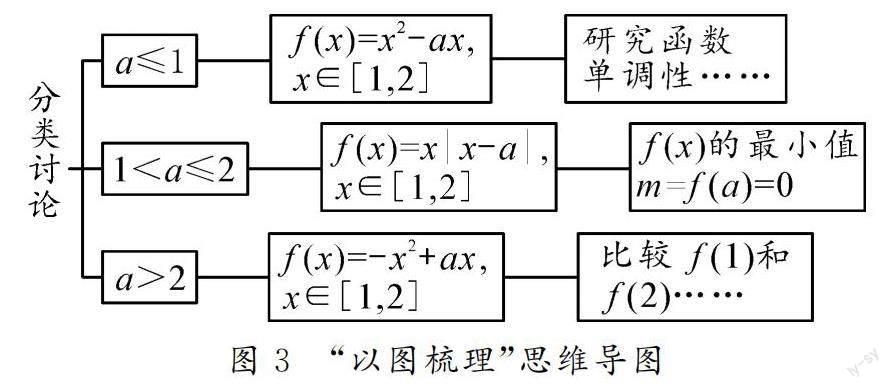
例3 已知a∈R,二次函数f(x)=x|x-a|,求f(x)在区间[1,2]上的最小值.
分析:该函数的关键为|x-a|的取值,结合定义域发现,此题需要运用分类讨论思想,根据a的取值分为三种情况讨论f(x)在区间[1,2]上的最小值.本题的思维较为复杂,如图3所示的思维导图可以帮助学生在复杂抽象的问题情境中明晰解题过程,绘制思维导图的过程也是拓展学生思维的过程.
4 借图发散,检验回顾
检验回顾是促进学生强化、内化知识的过程,在帮助学生检验问题解决准确性、梳理解题过程的基础上,引导学生归纳总结问题中蕴含的知识点,以及解决问题所运用的数学思想和方法,更新知识体系,同时思考是否存在更优化的解题方法,积累解题经验.
例4 某一运动服装专卖店,在8月份上市了新设计的运动套装,已知该运动套装的进价为180元/套,若售价为340元/套,则每月可以卖出50套,售价每下降10元每月就会多卖出6套运动套装,为了获得最大利润,现将每套运动套装降价x元(x为10的倍数),每月运动套装的销量为y(单位:套),月利润为W(单位:元).
(1)写出y与x之间的函数解析式;
(2)如何确定售价才能获得最大利润,最大利润是多少?
分析:第(1)问部分学生通过绘制思维导图(如图4),找到了y与x之间的关系,随即确定函数解析式为y=50+35x.在检验回顾环节,教师可以引导学生思考,得到除以上解题思路外是否还有其他解题方式,如比例法,同时,延伸比例法在相似图形解题过程的应用,拓展学生解题思路.
第(2)问考查二次函数最值问题,一般来讲,二次函数的最值在顶点处取得,但是也存在特殊情况.教师应有意识地引导学生根据实际问题具体分析自变量的取值范围,进而求出最大值或者最小值.
根据波利亚解题思想与思维导图的融合,在以图示意、按图索旨、以图梳理、借图发散的过程中,引导学生体验理解问题、拟定计划、执行计划、检验回顾的解题过程.一方面,帮助学生梳理解题思路,为学生指明解题思维方向,优化解题过程,发展和培养学生的解题能力;另一方面,在解题过程中促进学生重构数学知识结构、感悟数学问题所蕴含的数学思想方法.
参考文献:
[1]吴冬霞,桂改花.波利亚解题法与思维导图在立几证明中的应用[J].中学数学,2021(15):29-30,42.
[2]朱佳炜,任宏章.活用思维导图 助力微课生长——以“二次函数的图象、性质与系数的关系”微专题教学设计为例[J].中学数学月刊,2022(8):15-16,22.
[3]沈敏.思维导图在数学中考復习中的功能与应用策略——以二次函数复习为例[J].中学数学研究(华南师范大学版),2021(18):40-41.
[4]单雪昀.浅谈波利亚四步解题法在数学解题中的应用——以一道平面图形的动点问题为例[J].中小学数学(初中版),2021(4):17-19.
[5]贺文,夏小刚.波利亚解题思想对数学教学中“教思考”的启示[J].数学教学通讯,2022(12):16-18.
[6]温定.圆锥曲线“定值问题”的解题表设计探究——基于波利亚“怎样解题”的思想[J].数学之友,2022,36(11):85-87.

