两种混合模型对教师资格考试中学数学试题的性别DIF研究

罗成禹 杨宏博 刘惠玲

[摘要]教师资格考试在性别方面进行项目功能差异（DIF）研究十分重要。当前教师资格考试女生考生人数远远高于男生，即使是报考中学数学教师，女生人数仍约为男生的2倍。采用基于非参数模型的SIBTEST-观测分绘图法和基于参數模型的3PLM-GRM-特征曲线面积法，逐一分析2019年上半年中学数学初、高中2套试卷试题在男女性别上是否存在DIF。结果表明，2套试卷均未发现存在显著的DIF，可以判定教师资格考试中学数学试题对男女生是公平的。相较而言，SIBTEST-观测分绘图法操作简单，易于理解，是更可取的方法。

[关键词]教师资格考试；项目功能差异；性别；SIBTEST；3PLM；GRM

[中图分类号]G424.74[文献标识码]A

[文章编号]1673—1654（2023）05—021—010

项目基金教育部教育考试院“十四五”规划支撑专项课题“基于‘四有好老师职业内涵下的中小学教师资格考试大纲修订研究”（NEEA2021082）。

教育公平是社会公平的基础，是人生公平的起点，事关人民幸福、社会安定，对实现中国梦具有重要意义。作为教育“指挥棒”的考试，试题的公平性是大规模教育考试需要关注的重要问题。如果一项考试存在公平性问题，那么它的分数解释、做出的决定和结论都将是无效的、不合理的，甚至是有害的[1]。试题的有效性、稳定性和公平性是试题质量的重要方面，项目功能差异（differential item functioning）是衡量试题是否对某个群体有偏差现象的重要指标。若具有相同能力水平或熟练水平的不同群体考生对某个题目正确作答的概率不同，则这个题目就可能存在项目功能差异[2]。

坚守“促进公平，科学选材”的初心，维护国家教育考试公平，对教师资格考试进行项目功能差异分析十分重要。当下由于一些客观因素，我国中小学教师、师范院校学生存在着较为严重的男女比例失衡问题。单从教师资格考试男女生报考人数的比例来看，考生男女比例约为1∶5。女生的总体成绩和笔试通过率均高于男生，除男女考生群体本身在知识、能力等方面的差异外，是否有的试题是有利于女生而不利于男生？因此，研究教师资格考试笔试成绩的性别差异就具有非常重要的意义。

目前国内外关于项目功能差异的研究，绝大多数集中在0/1计分的题型上。对于多级计分题型的DIF检验方法多停留在理论研究上，要么方法过于复杂，要么存在一类错误较高、统计检验力较低的问题，缺乏样本量选取的依据，应用研究很少。实际工作中，尤其是对教育考试的研究中，试题既有0/1二级计分的客观题型，也有多级计分的题型，而且多级计分题型赋分占全卷总分比重较大是我国教育考试的一大特色。本研究针对中小学教师资格考试《数学学科知识与教学能力》进行项目功能差异的相关研究，并试图探讨一种“混合模型”，即0/1计分试题采用0/1评分模型，多级计分试题采用多级评分模型，以期获得一种高效、便利、直观的DIF检验模型，为教育考试DIF检验研究提供实际应用方面的参考。

一、研究对象与方法

（一）研究数据

选取2019年上半年中小学教师资格考试《数学学科知识与教学能力》（初级中学304、高级中学404）考生作答数据进行研究（见表1），初、高中数学实考人数男女生比例约为1∶2。

初、高中数学试卷均由17道题目组成，其中单项选择题8道，每题5分，共40分，可以统一按照二级计分的客观题来处理；其余试题均为多级计分试题，共110分，具体详见表2。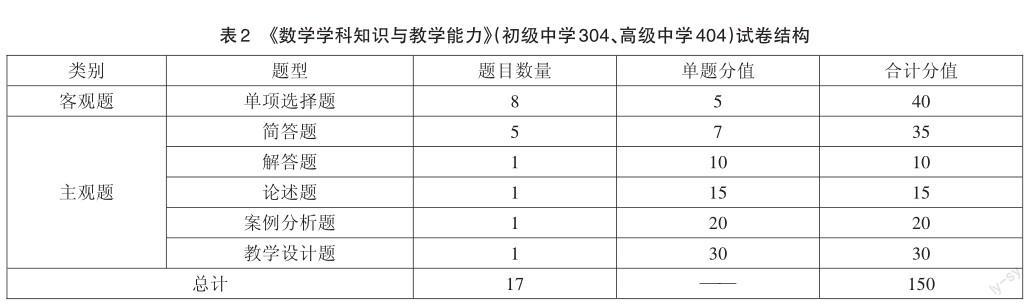

（二）研究方法

第一步，对男女考生的数学成绩进行描述性统计分析，对总成绩是否存在性别差异进行t检验。第二步，对考试分数的内部一致性信度和局部独立性进行检验。第三步，对所有试题是否存在DIF进行分析，并具体分析造成DIF的原因，以期进一步提升命题质量。在对试题DIF进行分析时，尝试采用两种混合模型，探索更适用于实际的DIF检验模型。

1.非参数混合模型：SIBTEST-观测分绘图法

教育考试主观题型常有10分（11评级）以上的大分值题型出现，不少模型常会出现数据溢出、拟合差、收敛慢的问题，使得很多测量软件有评分级数的限制，而等级反应模型没有评分级数的限制，是分析主观题的首选模型。根据题型的不同选择不同的模型对数据进行分析，并且模型中的参数标刻在同一量尺上。其基本思想是：对0/1二级评分题型用3PLM，对多级评分题型用GRM，依据局部独立性假设，2个模型计算的似然函数相乘得到一个总似然函数，从而保证3PLM与GRM的参数在同一量尺上[7]。

二、结果分析

（一）男女考生考试成绩差异分析

对参加2019年上半年中学数学考试的全体考生成绩进行统计分析，剔除零分试卷后，利用SPSS 25.0软件分析得到男女考生数学考试的平均分、标准差、2群体差异、t-检验效果量见表3。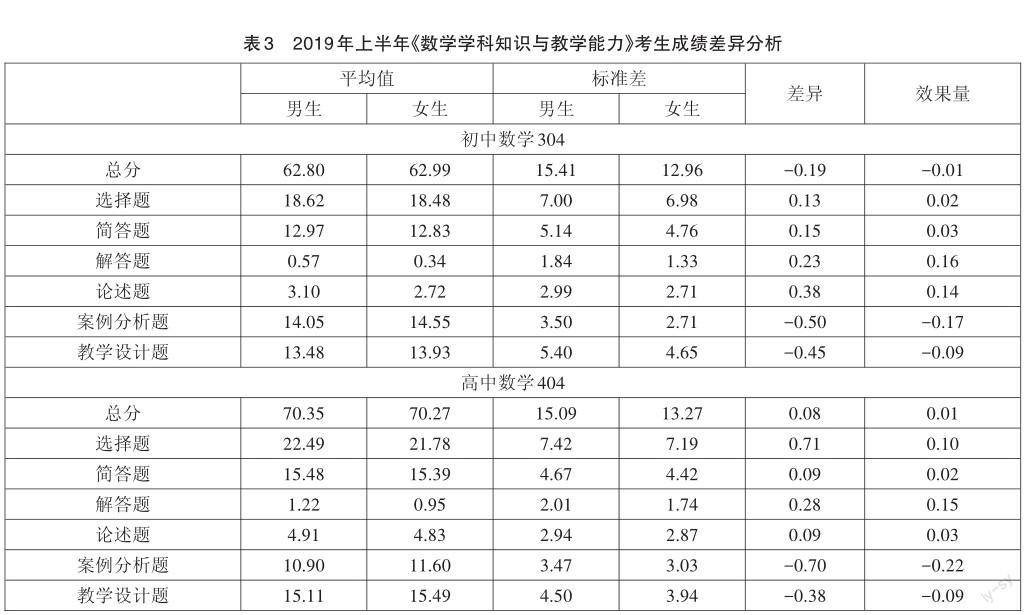

纵观全卷，无论是卷面平均得分还是各题型分项平均得分，男女考生群体相差都很小。除高中数学案例分析题效果量绝对值大于0.2外，其余初高中数学各题型均小于0.2，说明男女考生群体差异不显著。但仅凭这些数据并不能说明试题对于男女考生群体不存在项目反应差异，因为有可能在相同水平下，一部分试题对男生有利，另一部分试题对女生有利，相互抵消后表现出无DIF情况；也有可能男女考生群体整体水平存在差异，但因题目存在DIF而弱化了这种差异。因此，需要对试题是否存在性别DIF进行检验。

（二）内部一致性与局部独立性分析

分析结果表明，试卷内部一致性较高，从因子分析的结果看，第一特征值为第二特征值的3倍以上，基本可以判定中学数学试题是满足单维性的；同时，KMO检验值均大于0.7，说明因子分析的结果是具有统计学意义的。

（三）SIBTEST-观测分绘图法DIF检验结果

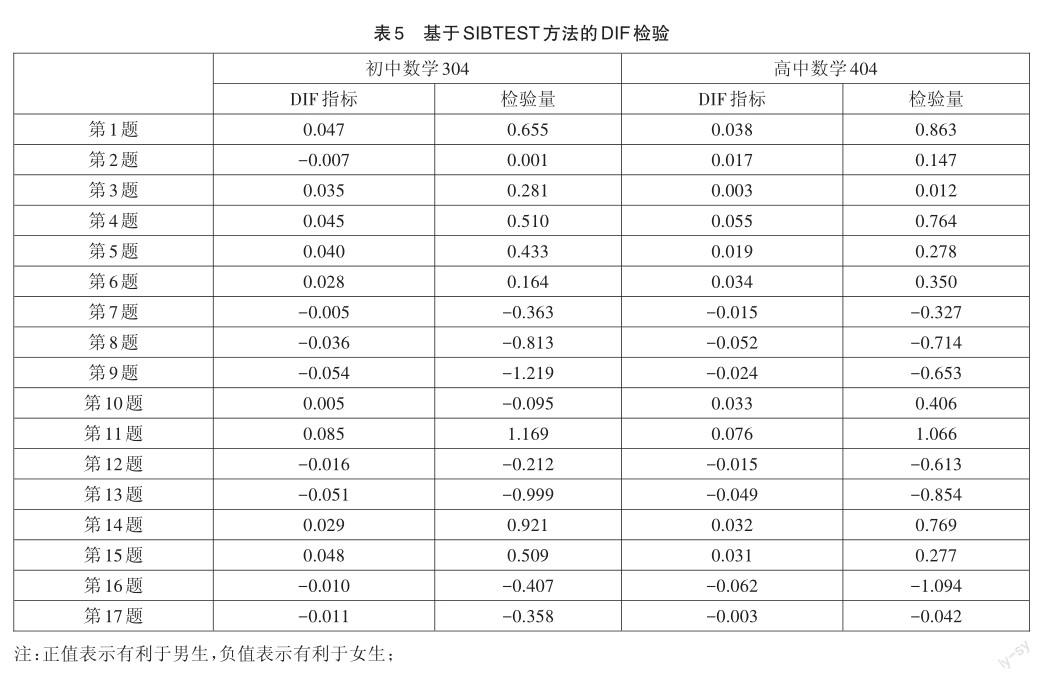
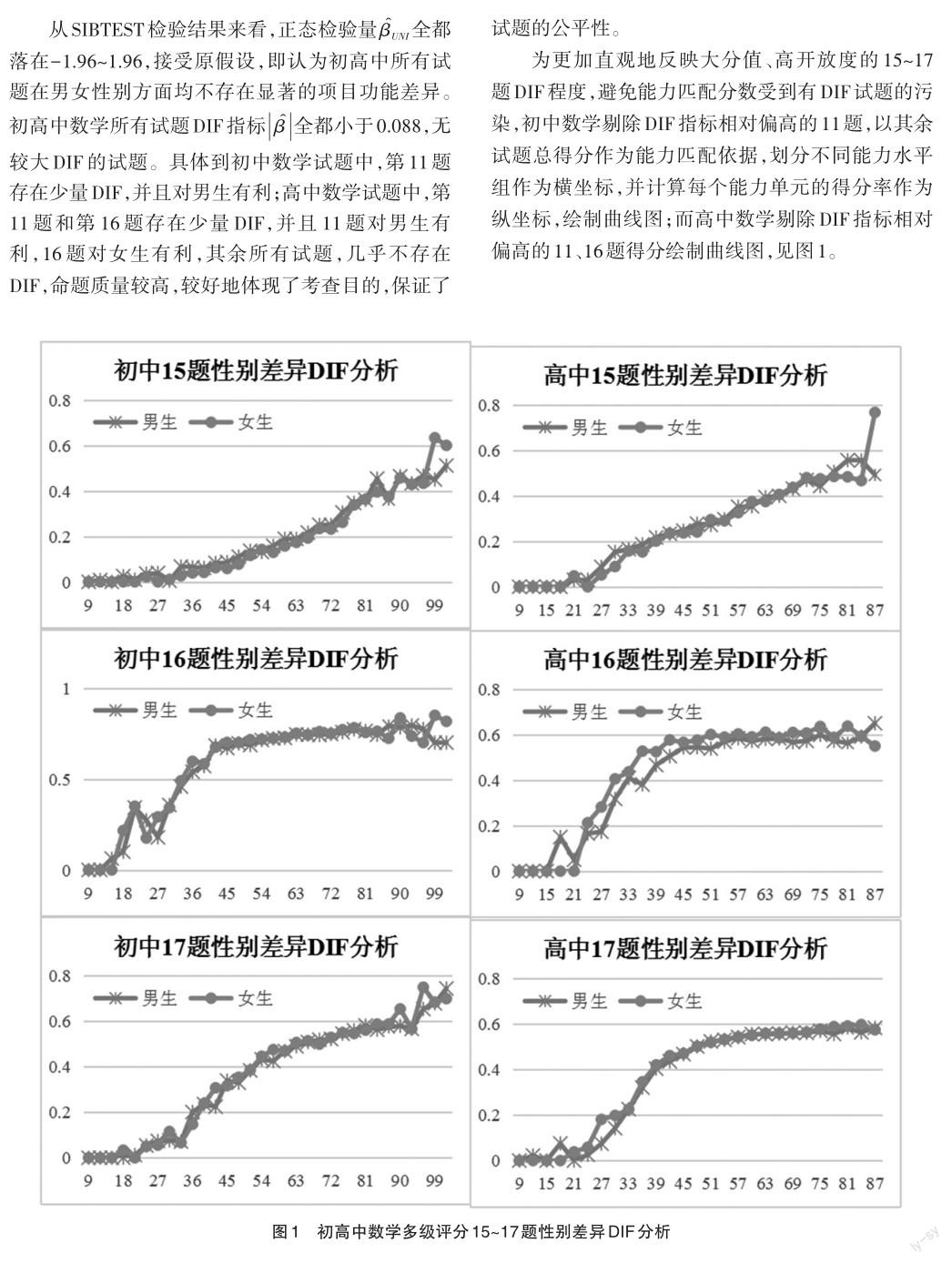
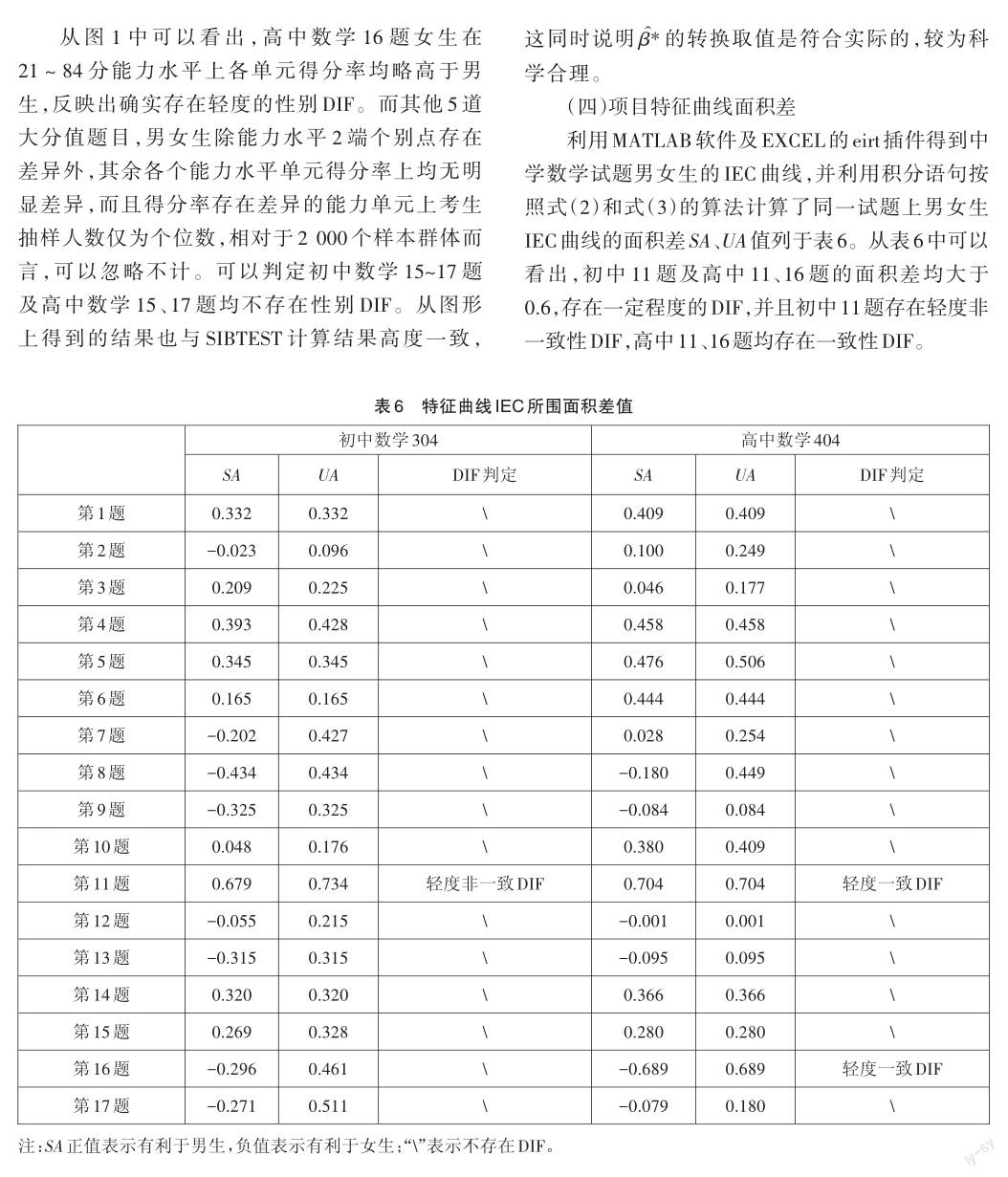
由于面积指标作为DIF度量指标最大的困难在于缺乏面积测度抽样标准误，这给评价任何所发现差异的显著性带来了困难。为了更直观地考察多级计分试题的DIF程度，本研究绘制了面积差法所检测出的3道试题按式（1）得到的IEC曲线见图2。3道试题确实存在一定程度的DIF，但差异并不显著。对照表5与表6的数据，无论是正负号还是数值的相对大小以及DIF检出率都高度一致，从不同角度不同方法验证了结果的一致性，再次证明2019年上半年中学数学试题在性别上均不存在显著的DIF。

三、结论与展望

以2019年上半年教师资格考试初、高中数学试卷为对象，分析在男女性别上的项目功能差异。结果表明，初、高中试卷中无论是客观题，还是主观题均未出现显著的项目功能差异，试题质量较高，较好地保证了考试在男女性别上的公平公正。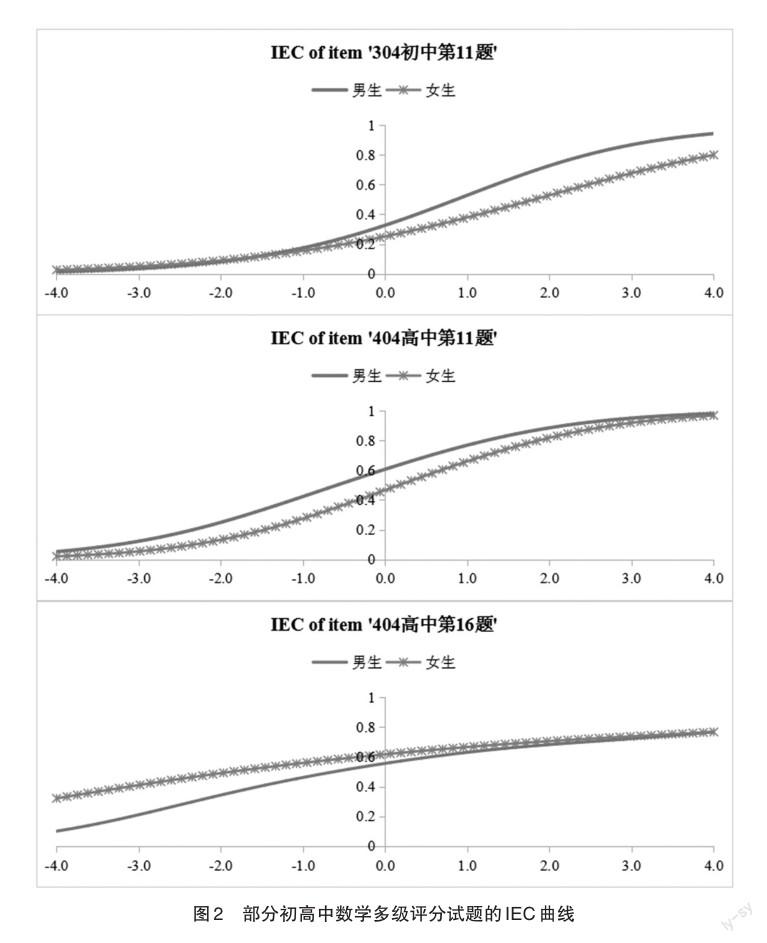

具体到试题方面，初中11题考查方程根的问题，属于学科知识代数内容，区分度达0.41，需要考生具有较好的转化能力和灵活应用能力；高中11题考查方程组解的问题，属于学科知识代数内容，区分度达0.43，需要考生具有较好的转化能力和推理论证能力；高中16题考查以教学提问为案例的分析题，属于教学能力教学评价内容，区分度达0.52，需要考生具有较好的分析能力、阅读能力、表达能力。有研究表明，男生在逻辑思维能力、空间想象能力、创新能力、推理和解决问题的能力方面以及需要多种解决策略的任务时具有优势；女生在运算求解能力方面具有优势，在完成计算技巧、记忆以及阐述性的任务上更好[12]。初高中11题由于数字设计较为巧妙，计算简单，难点在于转化和推理论证，可能对更擅长计算的女生较为不利；高中16题，表格式长篇幅的案例文字阅读可能对男生较为不利，存在轻度DIF主要是题型结构和考查内容的不同所致，并非试题命制的公平性造成差异。简答题语言规范简洁，表述清晰明确，案例题紧扣课堂教学，贴近教学实践，这3道试题难度适中，区分度高，仍是不折不扣的好题。

与西方国家以选择题等客观题为主的考试形式不同，我国的教育考试以大量大分值主观题为主，但当前国内外对于多级评分试题DIF的研究很少。本研究侧重应用给出了同时检验多个大分值试题DIF的新思路，未来在方法的合理性、理论依据推导上需要进一步讨论、研究、完善。在教师资格考试试题公平性问题的研究方面，除了性别外，城乡差异、地区差异、师范生非师范生差异等也值得进一步研究，不斷提升命题质量，维护教育公平，为国家科学选才。

参考文献：

[1]关丹丹，乔辉，陈康，等.全国高考英语试题的城乡项目功能差异分析[J].心理学探新，2019，39（1）：64-69.

[2] KIM M.Detecting DIF across the Different Language Groups in a Speaking Test [J].Language Testing，2001，18（1）：88-114.

[3]董圣鸿，等.三种常用DIF检测方法的比较研究[J].心理学探新，2001，（1）：43-48.

[4] FRENCH B F，FINCH W H，et al. Differential Item Functioning on Mathematics Items Using Multilevel SIBTEST [J]. Psychological Test and Assessment Modeling，2016，58（3）：471-483.

[5]张龙，涂冬波.多级计分题项目功能差异常用检测方法及比较[J].江西师范大学学报（自然科学版），2015，39（5）：441-448.

[6]杜文久.高等项目反应理论[M].北京：科学出版社，2014：61-68.

[7]涂冬波，蔡艳，戴海琦，等.项目反应理论新进展：基于3PLM和GRM的混合模型[J].心理科学，2011，34（05）：1189-1194.

[8]杨志明.考试公平性之题目及试卷功能差异探析[J].教育测量与评价，2017，（9）：5-12.

[9]朱乙艺，韦小满.DIF值和样本量对SIBTEST检测方法的影响研究[J].中国考试，2012，（9）：9-14.

[10]黃晓婷，韩雨婷，吴方文.高考语文作文试题的城乡公平分析[J].中国考试，2018，（2）：1-5.

[11]朱乙艺，韦小满.我国成就测验的项目功能差异研究述评[J].教育与考试，2012，（1）：78-81.

[12]李付鹏，宋吉祥，杜海燕，等.基于Rasch模型的高考数学性别DIF检验[J].中国考试，2019，（3）：43-47.

[13] LI H H，STOUT W. A New Procedure for Detection of Crossing DIF [J]. Psychometrika，1996，61（4）：647-677.

[14] Chalmers R Philip.Improving the Crossing-SIBTEST Statistic for Detecting Non-uniform DIF [J].Psychometrika，2018，83（2）：376-386.

Gender DIF Research on Math Subject of the NTCE Based on Two Mixed Model

Luo Chengyu Yang Hongbo Liu Huiling

National Educational Examinations Authority，Beijing，100084

Abstract：It is very important to conduct research on the Differential Item Functioning（DIF）of the NTCE in terms of gender.At present，the number of female test-takers in the National Teacher Certification Examination（NTCE）is much higher than that of male test-takers.Even if they are applying for mathematics teachers in middle schools，the number of female test-takers is still twice that of male test-takers.This study analyzes test gender fairness of the mathematics teaching abilities test in the first test of NTCE 2019 through conducting DIF analyses，which based on the SIBTEST-score drawing method and 3PLM-GRM-item characteristic curve area difference method.The result shows that no significant DIF values were found in the two NTCE papers between male and female test-takers. This paper considers that the SIBTEST-score drawing method is simple and easy to understand，and is a preferred method.

Key words：NTCE，DIF，Gender，SIBTEST，3PLM，GRM

（责任编辑：吴茳）