基于IRT框架采用Angoff法进行合格标准设置的探索

杨观惠 王晓慧

[摘要]学业水平考试分界分数的划定关系到教育决策的科学性和公平性，涉及标准设定技术。为探究在项目反应理论（IRT）框架下采用Angoff法进行合格标准设置，以某地区初中学业水平考试某学科的模拟考数据为分析对象，将专家第三轮打分结果作为“最低合格能力考生”的作答数据，与真实考生的数据汇总，进行IRT参数估计。最终以“最低合格能力考生”能力分数的平均值-0.85作为合格的分界分数，该合格分数线的信息量为28.13，专家判断与实际结果的Pearson相关系数为0.9，表明采用该方法进行标准设定具有较高的质量和推广性。

[关键词]标准设定；分界分数；合格分数线；Angoff法；学业水平考试；IRT

[中图分类号]G424.74[文献标识码]A

[文章编号]1673—1654（2023）04—059—008

一、引言

随着教育改革的深化，基础教育阶段各科目新版课标都明确了学业水平考试的学业质量水平，这为基于标准的教育考试提供了有利条件，使学业水平考试成为真正意义上的标准参照性测验。在考试实践中对分界分数的划定鲜有体现基于标准的理念[1]，这会影响考试结果的效度。目前常用的百分比法划定分界分数仅能提供学生在常模参照群体中的相对位置，无法提供说明学生知识、能力的信息[2]，考试结果仅能进行常模参照性解释，科学性和公平性难以保证。这也无法反映学校对课程标准的执行情况，对教育教学的促进作用有限，使学业水平考试的评价反馈作用和教育监测功能受到限制[3]。关于考试合格水平的标准，我国传统上用满分的60%作为合格分数线（简称“60分法”），60分法由于简单直观在校本考试和部分大规模考试中运用广泛。60分法是一种考前标准设置方法，在考试之前，文件规定了60分（含）以上为合格，60分以下为不合格。通过命题阶段的质量控制技术[4]，使刚刚合格考生的平均分接近总分的60%。若命题阶段没有做好命题质量控制，则会影响考试效度，有的考试用60分法仅是沿袭这一习惯，实际并没有与合格表现标准链接，没有合理规划试卷的难度结构，此时的60分就失去了意义，并不能代表达到合格水平。因此有些观点认为60分法仅是形式上的一致[5-6]。

标准参照测验的结果一般直接用于决策，如是否通过某项考核或能否获得资格证，标准设置可为决策提供依据[7]。要科学地对学生进行分类决策，标准的设置应当具有科学的依据和可操作的方法，能够被学界和社会同时认可与接受。探索合格标准设置方法有助于推动考试科学化，同时有利于促进学校认真执行课程标准，保障学业质量。

标准设置方法有很多，不同方法可能会产生不同的临界分数，对考试结果的解释也不同。在教育考试领域标准设置方法主要分为试题中心法和考生中心法[8]，前者是基于标准的判断，后者是基于常模的判断。试题中心法包括Angoff法及其变式、标签法、Nedelsky法、Ebel法等；考生中心法包括临界组法、对照组法等[9-10]。1971年提出的Angoff法是典型的试题中心法，也是最常用的标准设定方法，它的基本任务是界定各级别“最低能力考生”，对他们的表现标准达成共识，然后据此逐题判断各级别最低能力考生的得分情况[11]。若要确定合格分数线，则需界定“最低合格能力考生”群体应达到的合格水平表现标准。在划定分数的过程中将每一道试题与合格表现标准比对，若试题的能力要求低于或等于合格表现标准，那么“最低合格能力考生”应得分；若试题的能力要求高于合格表现标准，那么“最低合格能力考生”不得分。Angoff法的结果受专家的主观性影响，一般需要多位专家对试题打分，至少经过3轮打分直到估计值比较稳定为止，以最后一轮的结果作为分界分数[12]。由此可见，Angoff法在标准设定过程中将表现标准转化为试题的分界分数，实现与学业标准的连接，用该方法得到的分界分数可以有效地解释学生的学业水平是否达到合格。该方法在最大程度上兼顾了科学性和可操作性，是国际上应用最广泛的标准设定方法[13]，在我国主要运用于职业资格考试和大规模语言考试对标中[6-7，14-17]。

为贯彻基于标准的教育测量理念[2，18]，本文运用Angoff法和项目反应理论（IRT）将每道试题的能力要求与“最低合格能力考生”的能力水平进行对比判断，探索一种与合格表现标准链接的标准设置方法。在命题完成后组织专家对试题进行打分，该方法将Angoff法第三轮打分结果作为“最低合格能力考生”的作答反应数据，在IRT框架下估计“最低合格能力考生”的能力分数，以平均值作为合格的分界分数θ0，并进行分界分数的信度分析[19-20]和一致性分析。在學业表现标准不变的情况下，不同年度的考试通过等值技术[1，14，21-23]可以使用相同的能力分数作为合格分界分数，实现不同年度合格标准的稳定性和可比性。

二、研究思路与方法

（一）研究思路

运用Angoff法需要专家根据相应的表现标准来判断“最低合格能力考生”在每道试题上的作答表现。在判断前，要确定该学科的水平标准。根据新版课程标准，学业质量标准是对学生学业成就表现的总体刻画，是界定学科“最低合格能力考生”表现标准的依据。学科专家和评价专家运用赋分得分法判断出“最低合格能力考生”在每道试题上的得分；在IRT框架下估计“最低合格能力考生”的能力分数，并计算该能力分数的信息量和信度作为分界分数的质量指标。为验证标准设定的一致性，本研究对专家判断和实测结果进行相关分析[16]。

（二）研究方法

目前，我国初中学业水平考试的功能定位是“两考合一”“兼顾毕业和升学”，具有标准参照考试和常模参照考试的性质。单从升学角度看，标准设置获得一个可信的合格分界分数显得尤为重要。本研究以某地区初中学业水平考试某学科的模拟考数据为研究对象，采用改良Angoff法工作流程[23]组织7位专家判断“最低合格能力考生”在每道试题上的得分情况。每轮打分结束后进行汇总，对差异较大的试题进行讨论，再进行下一轮打分。以第3轮打分结果作为7位“最低合格能力考生”的作答反应数据，和真实考生的作答反应数据汇总在一起。使用R语言IRT分析工具，对该测验的试题参数、考生能力分数（θ）（包括“最低合格能力考生”的θ）进行估计[24]，计算不同能力分数（θ）的信息量I（θ）、误差Se（θ）和信度R（θ），并作图反映该测验的测量特征。以7位“最低合格能力考生”的能力分数的平均值作为合格的分界分数θ0，在信息量和信度图中呈现及解释合格分数线的位置及质量指标。一致性分析以分界分数上下一个测量误差范围的学生作为实际合格边界考生[25]，计算专家判断结果与实测结果的相关系数。

三、研究结果

（一）改良Angoff法赋分

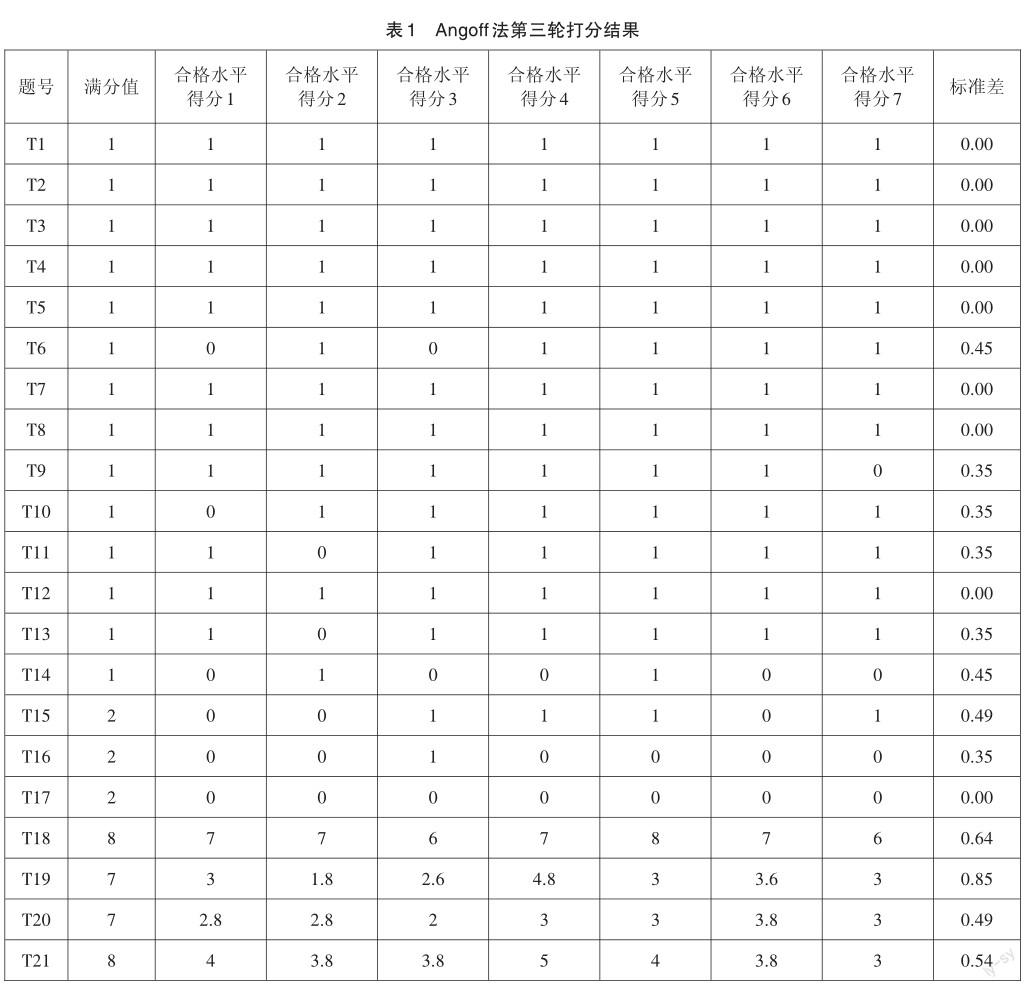
在改良Angoff法工作流程后，让专家根据合格水平的表现标准在设计的打分表上采用赋分得分法[12]判断“最低合格能力考生”在每个试题上的得分，例如某道试题满分分值为3分，若认为“最低合格能力考生”能得2分，则赋2分。经过三轮打分后，结果趋向稳定。将7位专家第三轮打分的结果作为“最低合格能力考生”作答反应数据，如表1所示。从标准差数据可以看到，大部分试题专家判断结果的内部一致性较高。

（二）项目反应理论分析

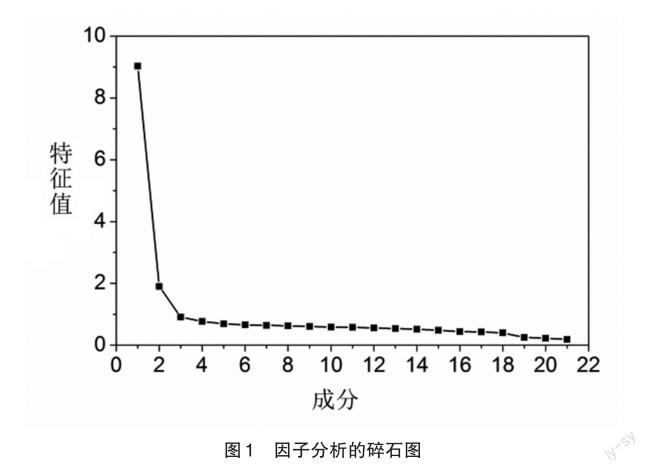
为确定测验的维度，通过SPSS对测验的各试题进行因子分析，碎石图如图1所示，第一特征值为 9.027，第二特征值为1.901，比值大于3，可以认为测验符合单维性假设[26]。

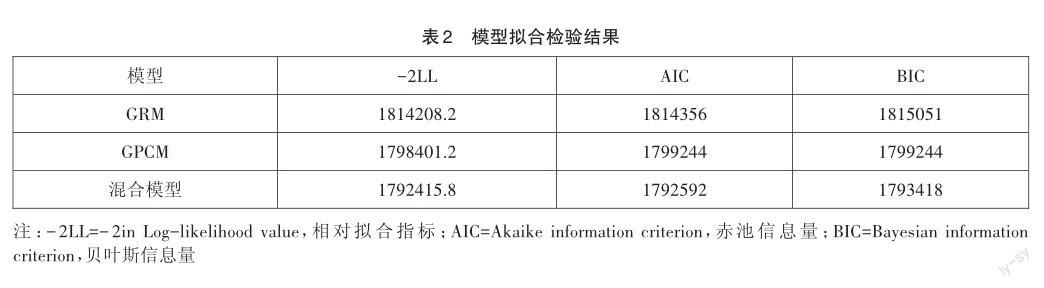
使用R语言对真实考生的应答数据进行模型拟合检验。测验中前14道题为单选题，为0—1计分试题；T15-T17题为不定项选择题，T18-T21题为简答题，属于多级计分试题。因此对该测验分别检验了单维等级反应模型（简称“GRM”）、单维分部评分模型（简称“GPCM”）和单维混合模型[27]（前14题采用 logistic三参数模型，3道不定项选择题采用GRM，4道简答题采用GPCM）的拟合情况，结果如表2所示。根据相对拟合指标值越小拟合性越好的原则[28]可知，混合模型拟合效果更好，因此根据该模型进行后续分析。

对试题进行局部独立性检验（Q3统计量）[24]，结果如表3所示，Q3统计量的值均小于0.36，可知所有試题满足局部独立的假设。

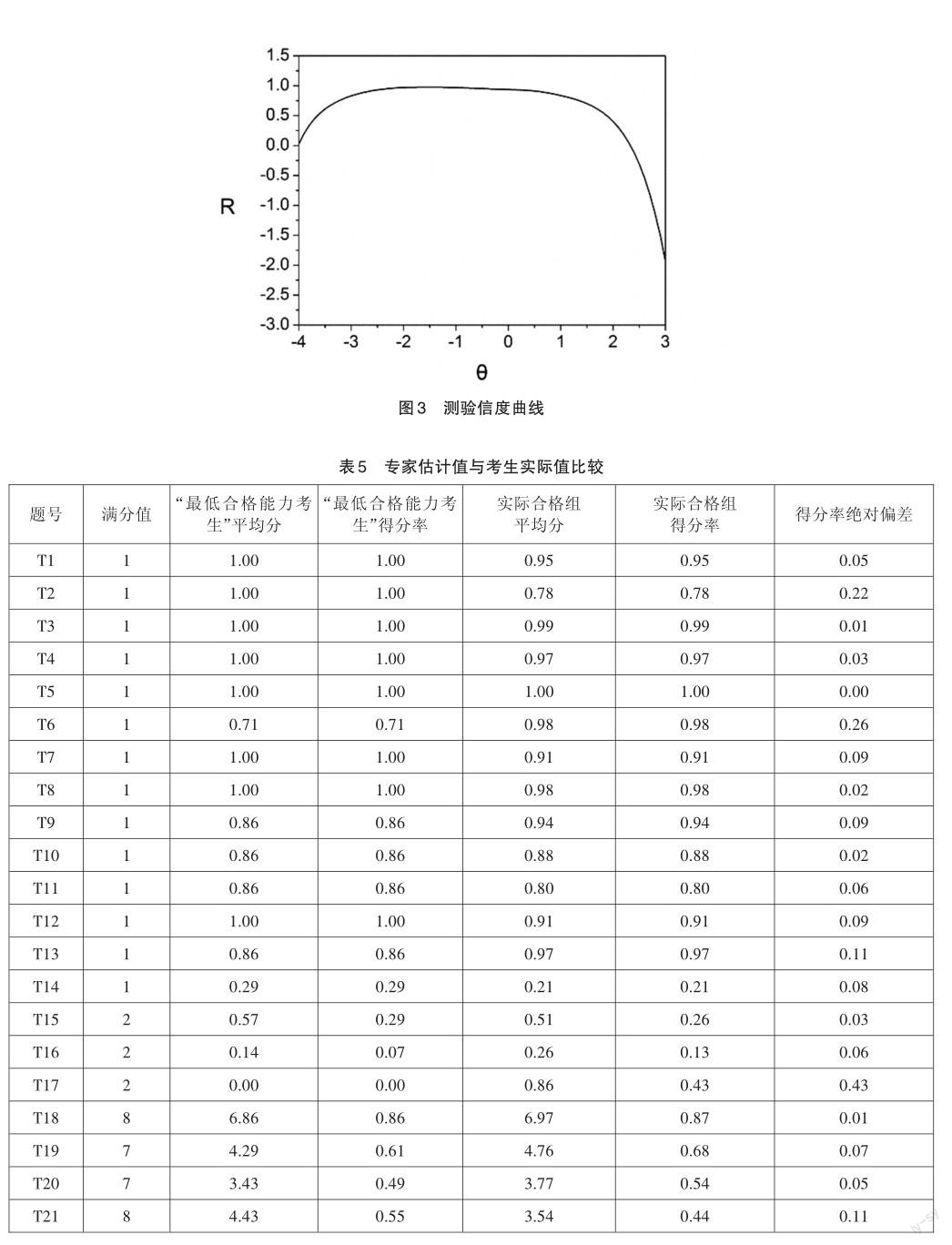
将7位“最低合格能力考生”作答反应数据和9895名真实考生的作答反应数据汇总在一起，共同作为本文的数据分析对象。IRT分析框架可以在同一量尺上估计试题的难度和学生的能力，使用R语言可得到试题的难度、区分度和猜测参数（单选题）的估计值以及每位考生能力θ的估计值。其中，7位“最低合格能力考生”的能力分数θ如表4所示，平均值为-0.85，以此作为合格的分界分数θ0。计算测验信息量I（θ）、测量误差Se（θ）和信度R（θ），并作图反映该测验的测量特征，测验信息与误差曲线如图2所示，参考线对应的θ为-0.85，测量误差为0.19；测验信度曲线如图3所示。

（三）一致性分析

为了检验改良Angoff法专家赋分结果的有效性，计算专家判断与实测难度（得分率）的相关性，以此作为标准设定的一致性证据。将能力分数在分界分数上下一个测量误差（-0.85±0.19）范围内的被试看作实际合格边界考生（简称“实际合格组”），统计专家判断的“最低合格能力考生”和实际合格组在每道题上的平均分、得分率和得分率绝对偏差，如表5所示。偏差较大的试题为T2、T6和T17，其余试题的判断绝对偏差在0.11以内。计算平均分与实际平均分（第3列与第5列）、得分率与实际得分率（第4列与第6列）的Pearson相关系数，分别为0.98和0.90，p值为0.000（显著相关），说明专家判断与实测结果高度一致。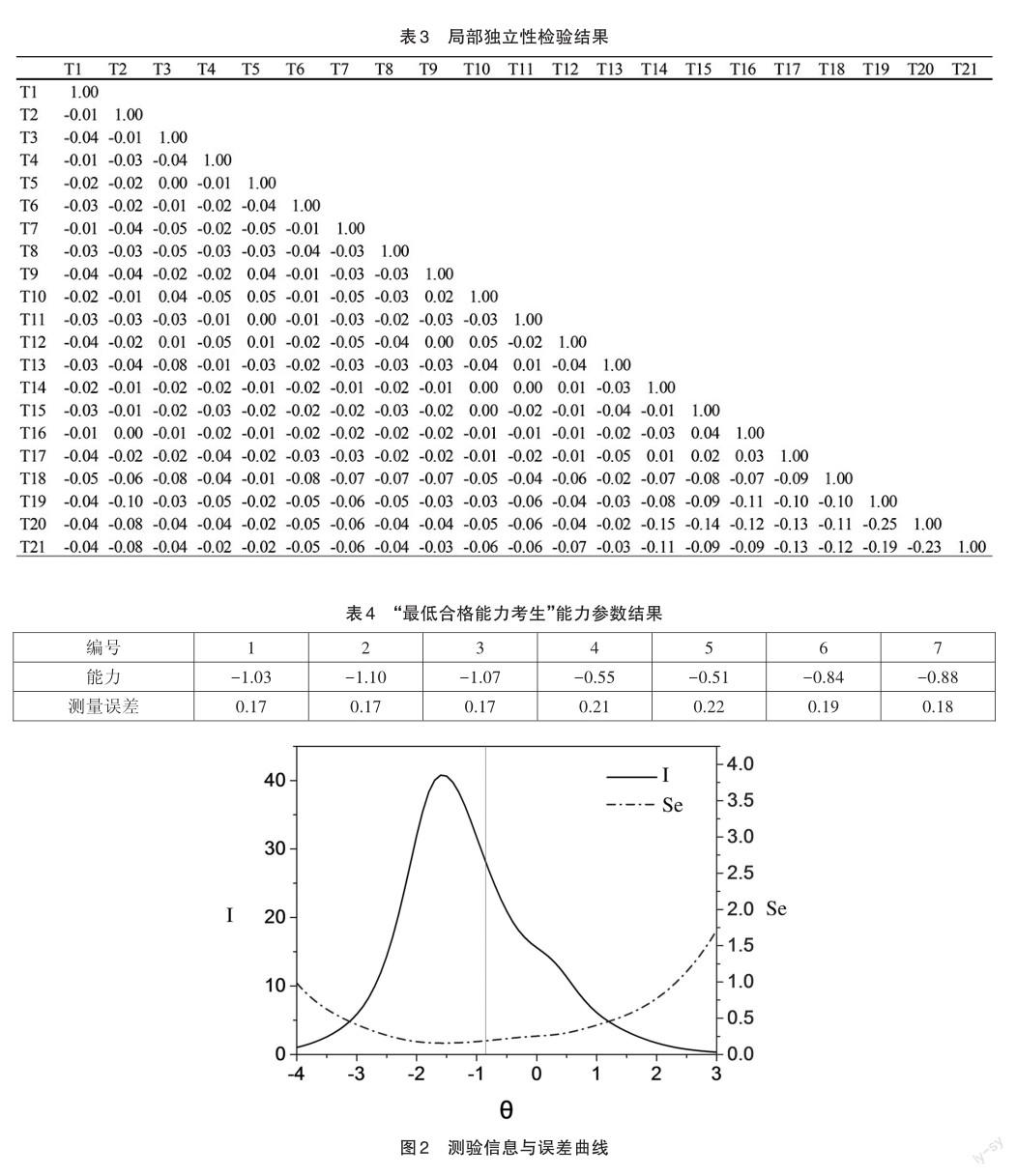

四、讨论

项目反应理论中，信息量反映测验的质量：信息量越大，对被试能力估计的误差越小。对于标准参照测验，应在分界分数及其附近有精确的估计和高区分的能力，信息量大于25表明测验质量理想[19]，因此可将分界分数点的信息量作为标准标定的质量指标。由图2可知，分界分数θ0的信息量I（-0.85）= 28.13，信度R（-0.85）=1-1/I=0.96，表明该分界分数具有较高的测量精度和区分能力，采用该方法进行标准设定的质量较好。在表现标准不变的情况下，不同年份的考试通过等值技术可采用相同的能力分数作为合格的分界分数，具有稳定性和可比性，容易被社会接受。

目前，基础教育阶段新版课程标准中都明确了各学科学业质量标准，为基于标准的教育与评价提供了有利条件。考试机构可以依据学业质量水平开发标杆卷，依据科学的标准设定方法划定分界分数，在每年的测验编制中做好等值设计，再通过等值处理将测验的分数转化为标杆卷的能力分数，由此可依据标杆卷的分界分数进行分类，避免频繁进行标准设定。

该合格标准设置方法目前仅使用模拟考数据进行了检验，尚未推广。一是Angoff法工作流程比较复杂；二是在分数解释时，需要有一定的测量基础才能够理解。因此，若在实际中进行推广，需要对利益相关者进行深入的科普和宣讲，并且需要教育行政部门的支持和广泛的社会认同。

学业水平考试分界分数的划定关系到教育决策的公平性和科学性，分界分数应具有较高的信度。本研究通过Angoff法工作流程组织专家界定“最低合格能力考生”并逐题判断他们在每道题上的得分，以此作为“最低合格能力考生”的作答反应数据，将这些数据和真实考生的作答反应数据汇总在一起，在IRT框架下进行参数估计。从能力参数估计的结果获得“最低合格能力考生”的能力分数θ，以平均值-0.85作为合格的分界分数，对应的信息量为28.13，表明分界分数具有较高的信度。专家估计值与实测值的相关分析表明专家判断与实际结果一致性较高，因此采用该方法进行标准设定的质量较好。该方法可推广至多个等级分界分数的划定或其他标准参照性考试。此外，通过等值技术可实现不同年度合格标准的稳定性，避免频繁设定合格标准。

参考文献：

[1]罗莹，韩思思.高考改革选考科目等级评定标准研究[J].教育科学研究，2018，（06）：11-14.

[2] Tognolini Jim，Stanley Gordon，杜承达.基于标准的评核：教育领域人力资本和能力提升的工具与方法[J].考试研究，2010，6（02）：4-20.

[3]宋宝和，赵雪.高中学业水平合格性考试的设计及价值分析[J].中国考试，2019，（01）：19-23.

[4]王晓华.基于标准的教育考试合格标准研究[J].教育科学，2012，28（05）：15-21.

[5]赵世明.科学确定专业人才资格考试的合格标准[J].中国人才，2007，（17）：66-67.

[6]景汇泉，郭永松，孙宝志，等.考试合格标准设置的国内外现状[J].中国高等医学教育，2007，（10）：56-57.

[7]汪存友.科学设定职业资格考试合格标准[J].中国考试，2012，（04）：43-47.

[8]余嘉元. Angoff方法有效性的检验研究[J].教育研究与实验， 2008，（01）：54-57.

[9]李珍，辛涛，陈平.标准设定：步骤、方法与评价指标[J].考试研究，2010，6（02）：83-95.

[10]向冠春.标准设定与等级划分[J].成人教育，2013，33（01）：14-20.

[11]闵尚超.接受型语言考试与语言标准对接的效度问题——一致性[J].现代外语，2019，42（05）：696-708.

[12]范士娟，王晓慧.上海市普通高中信息科技学业水平合格性考试合格标准划分初探[J].考试研究，2020，（03）：47-52.

[13]汪存友.ETS iSkills～（TM）测验的标准设定及其对NTET的启示[J].电化教育研究，2012，33（02）：59-64.

[14]汪存友.关于设定全国中小学教师教育技术水平考试合格标准的思考[J].中国远程教育，2013，（03）：49-53.

[15]闵尚超，姜子芸.校本听力考试与《中国英语能力等级量表》对接研究[J].外语教学，2020，41（04）：47-51.

[16]张洁，王伟强.接受型语言考试与语言标准对接的效度问题——来自标准设定过程的证据[J].现代外语，2019，42（05）：684-695.

[17]何惧，何佳，安滔，等. Angoff法及其衍生方法在資格考试合格线设定中的比较研究[J].中国考试（研究版），2007，（06）：23-26.

[18]雷新勇.学业标准——基于标准的教育改革必须补上的一环[J].上海教育科研，2009，（06）：15-18.

[19]温红博，卜文娟，刘先伟.初中学业水平考试中固定比例法标准设定的信度分析[J].考试研究，2017，（05）：55-63.

[20]江西师大现代教育和心理测量通用分析系统研制组，漆书青，周骏，等.用信息函数法对标准参照测验作质量分析[J].心理与行为研究，2003，（01）：34-39.

[21]杨志明.学业水平考试事后等值的概念、条件与设计[J].教育测量与评价，2016，（11）：4-8.

[22]杨志明.做好高中学业水平考试所必须的四项测量学准备[J].中国考试，2017，（01）：8-13.

[23]杨志明.高中学业水平考试等级设定的若干方法[J].教育测量与评价，2016，（10）：4-9.

[24]罗照盛.项目反应理论基础[M].北京师范大学出版社，2012.

[25]汪存友，余嘉元，张颖.调和Angoff法在设定执业医师资格考试分数线中的应用[J].中国考试，2011，（10）：38-43.

[26] Slocum S L. Assessing Unidimensionality of Psychological Scales：Using Individual and Integrative Criteria from Factor Analysis[D]. University of British Columbia，2005.

[27]涂冬波，蔡艳，戴海琦，等.项目反应理论新进展：基于3PLM和GRM的混合模型[J].心理科学，2011，34（05）：1189-1194.

[28]单昕彤，谭辉晔，刘永，等.项目反应理论中模型——资料拟合检验常用统计量[J].心理科学进展，2014，22（08）：1350-1362.

Exploration of Qualified Standard Setting with Angoff Method Based on IRT Framework

Yang Guanhui Wang Xiaohui

Shanghai Municipal Educational Examinations Authority，Shanghai，200433

Abstract：Setting cut-off scores for the academic proficiency test is related to the scientificity and fairness of the educational decision-making，which involves standard setting techniques. This study explored the adoption of Angoff method for the qualified standard setting according to Item Response Theory（IRT），taking the mock test data of a subject in the junior high school proficiency test in a certain area as an example.The experts third round scoring results were used as the response data of the "minimum qualified candidates"，and the data of real candidates were put together for parameter estimation by R. The average of the ability score of the "minimum qualified candidates" is -0.85. Taking it as the qualified cut score，the information content of this point is 28.13. Additionally，the Pearson correlation coefficient between expert judgment and actual result was 0.9. The results showed that this method had high quality in standard setting.

Key words：Standard Setting，Cut Score，Passing Score，Angoff Method，Academic Proficiency Test，IRT

（责任编辑：吴茳）