国内基础教育及高等教育数学试题难度研究的文献综述

杨聪聪 闫芳

[摘要]运用内容分析法、文献计量法，借助VOSviewer软件，对国内基础及高等教育数学试题难度研究的文献进行综述。在知网数据库中搜集并筛选获得关于数学试题难度研究的期刊文献130篇，从文献的期刊来源、年份分布、作者情况、关键词分布、研究内容、评估方法6个维度进行剖析，发现研究总体呈上升趋势，但期刊较分散、各刊发文量较小、核心期刊文献较少，近年来多采用比较研究的方法对综合难度系数模型、数学核心素养等热点问题进行研究。据此，对未来研究方向提出加强义务教育阶段和高等教育阶段数学试题难度研究，通过合著提高研究质量、研究内容及预估算法应当更加多样化等建议。

[关键词]数学试题难度；综合难度；内容分析法

[中图分类号]G424.74[文献标识码]A

[文章编号]1673—1654（2023）04—040—013

作者简介杨聪聪，学科教学（数学）硕士研究生，云南师范大学数学学院；闫芳（通讯作者），博士，副教授，云南师范大学数学学院。云南昆明，650500。

一、引言

2019年《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》指出，科学设置试题难度，命题要符合相应学业质量标准，体现不同考试功能，建立命题评估制度，提高命题质量[1]。2020年新一轮高考改革启动，高考数学试题由文理分科逐渐向不区分文理过渡。新高考数学全国卷从2020年在山东省和海南省试用，到2021年使用省份已增加到10个。另外，2021年高考数学还将以往高考的全国Ⅰ卷、Ⅱ卷进行合并，统称为全国乙卷，全国Ⅲ卷改为全国甲卷。2022年的高考数学试卷类型、使用省份与2021年保持一致。到目前，北京、上海、天津、浙江高考数学科仍然采用自主命题。在此大背景下，高考数学试题的难度越来越受到学生、家长、教师以及广大数学教育者的关注。不仅如此，鉴于高考制度目前仍然是我国教育的“指挥棒”，高考数学改革也会影响到其他教育阶段的考试评价，其试题难度是否也会发生相应的变化？这是目前有待探究的问题。

试题难度是评价试题质量的一个重要指标，无论是对于教学过程中的教学测量，还是最后高考的选拔性考试都有着很大的影响。我国大规模教育考试试题难度的预估和控制非常敏感，既是科学问题，也是社会问题[2]。一份高质量的试题，一定具有良好的信度、效度、区分度以及适当的难度，使之达到教育测量的预定目标。怎样才能编制出一份高质量的试题呢？毋庸置疑，这首先与出题者的经验有很大关系，如果出题者有丰富的教学经验、先进的教育理念，一定能够让试题的质量大大提高。但是单纯依靠经验是不够的，试题质量还必须依赖于试题本身所反映的客观信息。如果能够挖掘试题中潜在的客观信息，提前较为准确地预知试题的各个评价指标，那么命题者就可以根据预知指标有针对性地对试题作出调整，进而提高试题质量。可见，建立客观、科学、合理的试题难度评价体系及模型十分有必要。本研究基于国内已有的对数学试题难度研究的文献，总结国内的研究现状及研究动态，发现需要改进或进一步研究的问题，提出未来研究的方向，以期为数学试题难度研究提供一定的参考。

二、研究方法

通过知网分别以“数学试题难度”“数学综合难度”为主题词，搜索期刊论文，共获得143篇文献，经过研读和筛选排除掉关联性较小的文献，最后保留130篇研究文献。运用内容分析法、文献计量法，并借助VOSviewer软件对这些文献进行整理综述。主要从期刊来源、年代分布、作者情况、关键词分布、研究内容、评估方法6个维度进行剖析，总结国内关于数学试题难度研究的基本状况，分析尚存的问题，提出未来研究的方向。

三、结果与讨论

（一）期刊来源

通过整理和统计发现，130篇文献分别发表于73种不同的期刊，其中发表相关文献超过2篇及以上的期刊有19种。130篇文献中有47篇发表于核心期刊，占总发文量的36.2%。其中有19篇文献既属于核心期刊，也属于CSSCI期刊，占总发文量的14.6%（如表1所示）。由以上数据能够看出：一方面，目前国内发表有关数学试题难度研究的期刊较多，但是大部分都只是发表1篇相关文献，连载量较少；另一方面，有关数学试题难度研究的文献发表于核心期刊的量较少，仅占总发文量三分之一多一点。总体来看，国内发表数学试题难度研究的期刊较分散，载文量较少，发表于核心期刊的文献较少，相关研究的质量有待提高。

（二）年份分布

为了分析数学试题难度问题研究随时间发展的趋势，图1给出了相关文献发表年份分布图，从图中能够直观地看出，国内数学试题难度相关研究开始于1987年，在2008年之前发文量一直较少，只有2001年发文4篇，2008年后相关研究的增加趋势明显。究其原因，自2000年以来，中国大范围地启动了基础教育课程改革工作。2004年我国实施新课改，考试内容增加了对知识的综合理解以及运用知识分析、解决实际问题的能力的考查，剔除了“偏、难、怪”试题，保证了试题具有适当的难度和较好的区分度。特别是从2007年开始，我国首次进行了高中课程标准改革后的科目设置与命题，其主旨是考试科目设置与内容要契合教学目标的改变，符合“三维”教学理念与人才培养目标，考试内容突出了基础性、时代性、选择性的特点[3]。2012年，教育部提出在统一高考基础上，积极探索建立符合高校自身培养目标和要求的创新人才选拔标准，完善多位一体的高校人才选拔综合评价体系[4]。2016年教育部成立了高考考试内容改革专家委员会，对高考内容改革进行战略性研究与顶层设计，以保证科学、公平、合理、有效的考试内容，全面突出我国创新人才选拔与培养的目标[3]。2020年实施新一轮高考改革，其中一大变化就是不分文理科。除自主命题省份，高考数学全国卷历来分文理科，但2020年首次在山东和海南采用不分文理科的数学新高考全国卷。2021年采用新高考全国卷的省份增加到10个，另外将全国III卷改为全国甲卷，将全国I卷和II卷合并为全国乙卷。从以上的相关教育政策或高考改革政策可以发现，这些政策的颁布对试题难度研究的热度有很大的导向作用，每个政策提出的当年或后一两年，一般都会成為研究热度较高的年份。

（三）作者情况分析

1.作者单位类型分布

图2直观呈现了作者单位类型分布情况。可以看出，关于数学试题难度的研究绝大部分集中在高等院校（66篇），其发文量达到总发文量的50.8%；然后是中小学（37篇），占总发文量的28.5%；再次是教研机构（17篇），占总发文量的13.1%；最少的是这三类机构间的相互合作发文，仅占总发文量的7.6%。在高等院校的66篇文献中，有50篇来自于师范类院校。究其原因，师范类院校以培养教师等教育行业从业人员为人才培养目标，其教学、科研等比较关注国家教育政策、高考改革以及试题调整等各方面的变化，因此师范类院校对这方面的信息比较敏锐，进而相关研究也较丰富。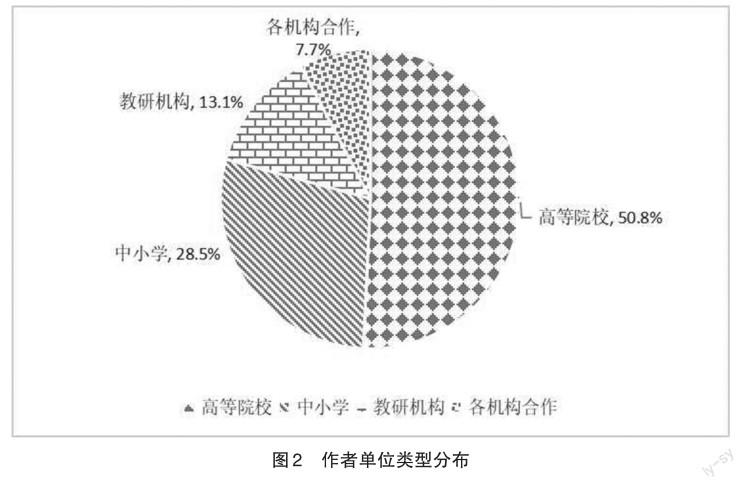

从以上分析可以看出，各机构间的合作研究较少。各高校师生虽然对国家教育政策、高考改革以及试题调整等各方面的变化比较敏锐，但是考虑问题多从理论出发，缺乏一定的实践基础。一线教师长期从事中小学教学工作，对政策的实施、试题的变化等有更切实的体会，对学生的实际情况更加了解，这些实践经验都有利于数学试题难度的相关研究。另外，相关的教育研究机构可以根据每年学生统考的情况，掌握大数据信息，这对数学试题难度的研究来说是非常重要的资源。因此各机构间若能够加强合作，相信对于数学试题难度的研究会大有助益。

2.作者合著情况

图3显示了作者合著情况。可以发现，目前相关研究以单人为主（65篇），其次是两人合著（32篇），接下来是三人合作（25篇），四人及以上合著的较少。另外，在多人合著（3人及以上）中，基本都是高校研究生与导师或研究生与研究生的合著，也有教研单位的多人合作，涉及高校师生与教研人员、高校师生与一线教师的合著很少。

一门学科的发展离不开团队，尤其是多人（3人及以上）参与的团队合作，群体成员间的共同努力会产生强大且持久的力量，期待未来的相关研究主体会有更多的“多人团队”出现，以此壮大和发展该领域的研究实力与学术地位。

（四）关键词分布

关键词频次可用于判断数学试题难度研究的热点、层次、趋势以及有待探讨的方面。利用VOSviewer软件，对130篇文献进行关键词分析：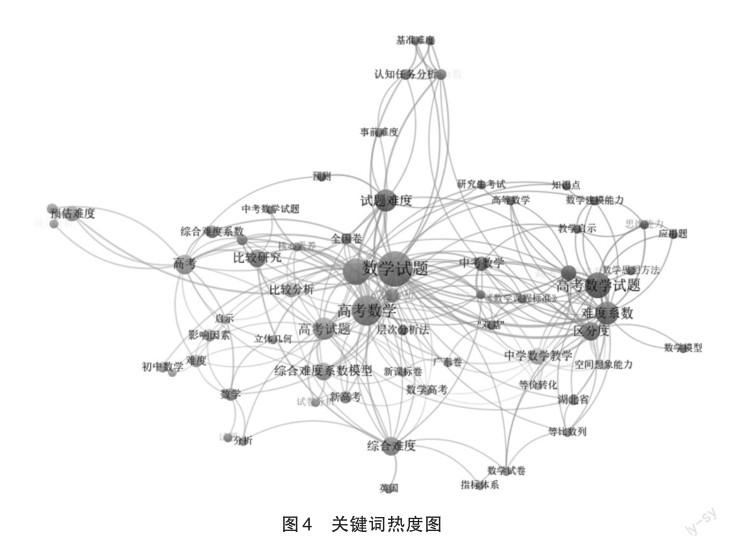

从图4能够清晰地看到关于数学试题难度研究热点，出现频率较高的关键词依次有（点越大代表该关键词出现的频率越高）：数学试题、高考数学、综合难度模型、高考数学试题、难度系数、试题难度、区分度、比较研究等。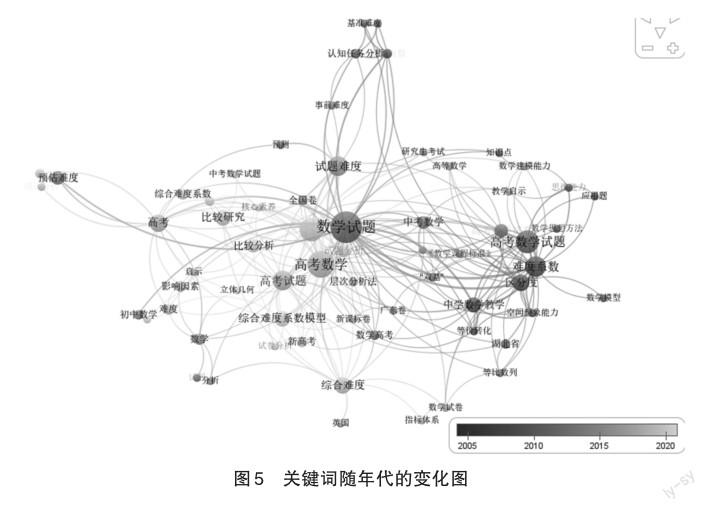

图5颜色的变化显示出关键词按照年份热度变化的情况，近几年的研究热点集中在浅灰色区域，关键词包括综合难度系数模型、数学核心素养、比较分析，其热度图依次如图6、图7、图8所示。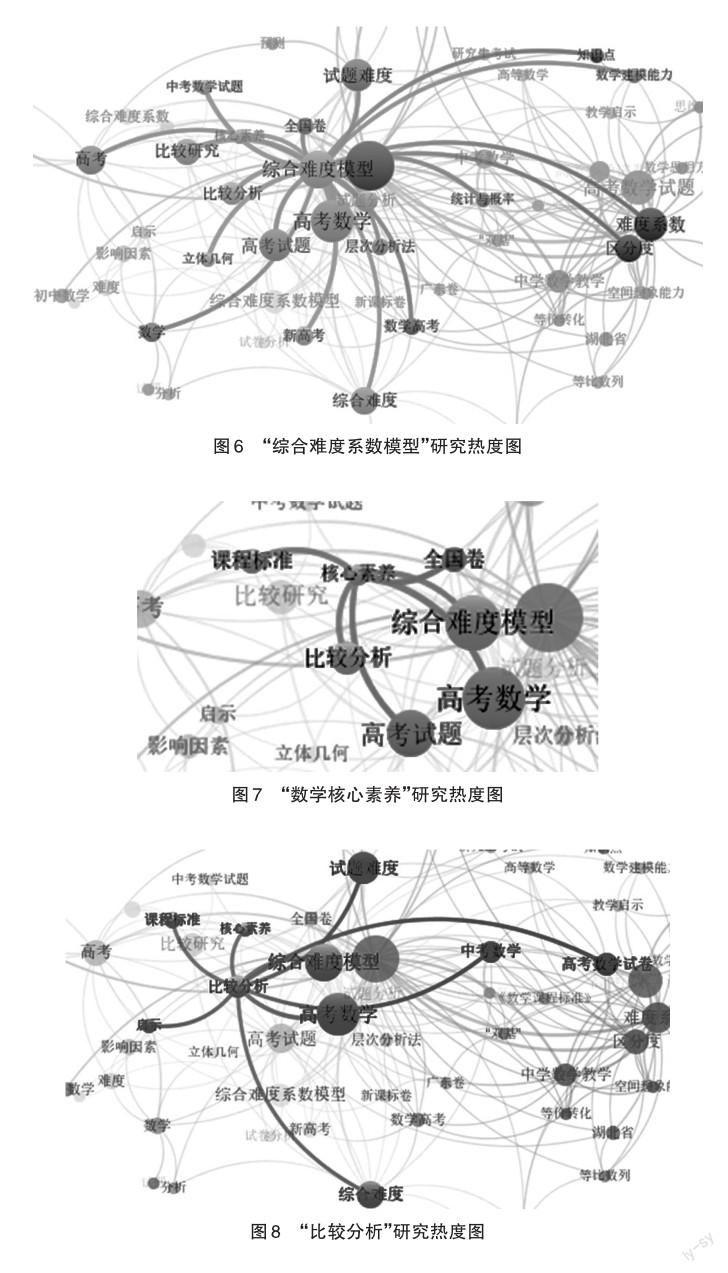

可见，近几年研究热度较高的问题是综合难度系数模型、数学核心素养，采用较多的方法是比较研究。

通过对以上关键词进行分析可以发现：

1.关于数学试題难度的研究，多以高考数学试题为研究对象，详见表2。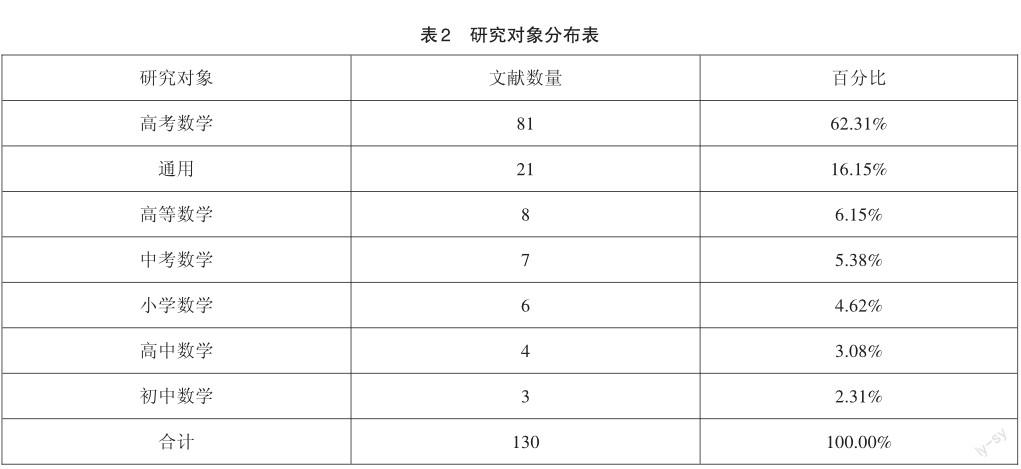

研究对象最多的为高考数学试题，其次是对数学试题难度的整体研究，即未注明具体学段，高等数学试题、中考数学试题和小学数学试题方面的研究基本持平，对于初中和高中平时检测的试题难度研究则较少。这也反映了相关研究中有待加强之处，一方面高考数学试题和学生平时的检测试题由于其考查目的不同，所以难度设置等各方面存在差异，将高考数学试题难度的研究结果直接应用于学生平时的检测试题可能会产生偏差，所以对于学生平时测验试题难度的研究可以作为后期研究的一个切入点。另一方面随着减负政策的出台，中小学生作业负担和培训负担问题得到全面整治，这一政策将如何影响义务教育阶段试题难度的变化还有待探究。2009年，《国家中长期教育改革和发展规划纲要（2010—2020年）》提出要“提高人才培养质量，着力培养信念执着、品德优良、知识丰富、本领过硬的高素质专门人才和拔尖创新人才”。作为当前检测人才培养成果方式之一的高校课程考试能否有效检测出学生的水平？其试题难度在发生怎样的变化？目前与此相关的研究较少。因此，还需加强义务教育阶段和高等教育阶段数学试题难度的研究。

2.近几年学者研究较多的内容是综合难度系数模型与数学核心素养。鲍建生教授于2002年在《中英两国初中数学期望课程综合难度的比较》[5]中首次提出了数学题的综合难度模型，随后有不少研究者基于此模型对试题或试卷难度展开探究。本研究的130篇文献中，有20篇引用了鲍建生教授2002年的研究成果，有15篇引用了2014年王建磐教授和鲍建生教授共同发表的《高中数学教材中例题的综合难度的国际比较》[6]，还有19篇引用了武小鹏和张怡2018年共同发表的《中国和韩国高考数学试题综合难度比较研究》[7]，这几篇文献都是关于数学试题综合难度的研究。其中前两篇发表于《全球教育展望》，第三篇发表于《数学教育学报》，均属于北大核心和CSSCI期刊，具有权威性。数学试题综合难度研究使得试题难度的评价更为全面、科学、客观。

另外，自2017年高中数学课程标准中明确提出高中数学教育要注重培养学生的6大核心素养以来，基于核心素养展开研究的课题较多，试题难度是其中一个。有研究者基于核心素养视角探析数学试题难度，使难度的衡量更加符合时代要求[8]。

3.对于数学试题难度的研究近几年多采用对比研究的方法，这与数学试题综合难度的计算方法有很大关系。数学试题综合难度的研究多是分析影响数学试题难度的因素，然后根据各因素对综合难度的影响大小，给予不同的权重并进行赋值量化。虽然这种方法使得试题难度评价更为全面，但是利用这种方法得到的难度单独呈现出来时，其意义比较模糊，综合难度系数本质上反映的是试题的绝对难度，它能够在多大程度上反映相对难度（事后难度）则难以明确，只有当几套试题放在一起进行比较时，其优势才能够体现出来，即较为清晰地比较出几套试题的难度差异。由此可见，进一步探究绝对难度与相对难度的关系十分必要，只有明晰二者的联系，才能够更好地利用绝对难度来预估相对难度。

（五）研究内容分析

通过对130篇文献进行整理，可将其研究内容划分为8大类（如图9所示），分别是绝对难度（试题本身的客观难度，即指从试题的背景因素、知识点含量等客观角度对试题难度进行评价）、试题整体分析、相对难度（试后的统计难度）、绝对难度与相对难度二者结合、影响因素、试题库、数学试题难度文献综述，以及其他的相关研究。其中研究较多的是绝对难度（57篇），其次是试题整体分析（24篇），然后是相对难度（12篇）、二者结合（11篇），影响因素的相关研究有8篇，试题库、文献综述的研究较少。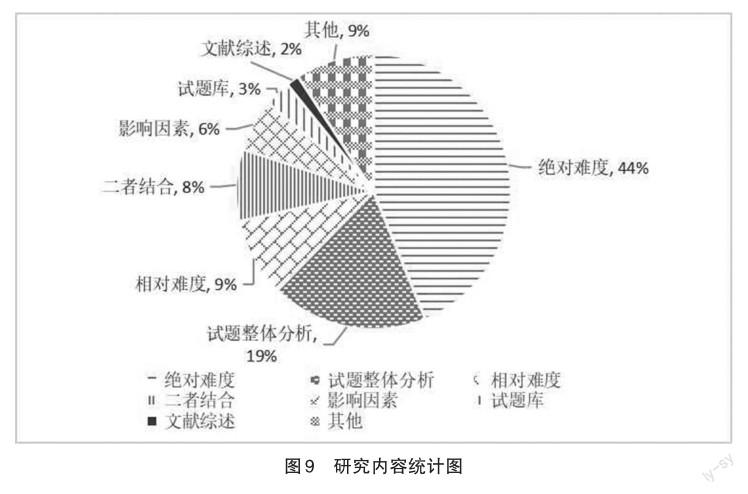

在绝对难度研究方面，研究者多对影响数学试题难度的因素进行水平划分，然后针对具体试题进行绝对难度的计算。王秋海教授结合实践并吸收国内的先进经验，得到了一种数学试题客观难度测量方法——EQR法，对知识点类型和应用方式进行赋值[9]。林雪明以潜在倾向理论为基础，结合区分度算法，提出了一种新的建立和实现试题难度系数数学模型的方法[10]。李二霞、邵志芳在前人设计的对试题难度进行事前评定的框架和实施程序的基础上，将试题的事前难度进一步划分为基准难度和解决难度，使得评价更为科学合理[11]。曾建国应用SOLO分类理论，从知识点考查的视角来评价高考数学题，并以三角函数模块为例进行评价分析[12]。张碧霞等人结合核心素养，对综合难度模型进行改进，分析在背景因素、认知水平、运算水平、推理能力、知识含量和数据分析的不同水平上的差异[13]。张玉环等人采用定性和定量相结合的方法，对2015年至2019年中国高考理科数学全国Ⅰ卷与法国本土业士考试（也称毕业会考）试卷进行难度和典型案例分析[14]。韩金璇等人运用综合难度模型对美国大学入学考试试题与中国高考试题进行对比分析，发现中国高考试题的推理因素难度较大，美国大学入学考试试题的背景因素难度较大，二者在参数因素上相差不大[15]。

对于相对难度的研究往往以学生试后成绩为基础，结合经典测量理论或项目反应理论，对试题进行难度、区分度等指标的分析。昌国良分析了2002年至2006年部分高考数学试题的相对难度，发现部分高考数学试题的难度偏离国家规定的标准，由此对高考数学试题的编制提出相关建议，以便更好地体现新课程改革的理念和创新精神[16]。李瑛基于经典测量理论，通过设定标准选择当年参加高考的少量学生入围进行试测，结合对试测生实测数据的分析，达到预测试卷难度的效果[17]。张天德等人利用双向细目表分析了2021年新高考数学I卷的知识点、关键能力、学科素养、情境等考查情况，另外结合山东省高考数学学科的成绩统计，分析了题目的难易程度，并在此基础上提出2022年新高考的動向以及备考策略[18]。

将相对难度与绝对难度进行结合的研究，一般是先结合评价框架进行绝对难度预估，然后再结合相对难度，分析二者的关系。周华辅采用累加点表估计难度，并将预估难度和实测难度进行比较，预估效果较好[19]。王晓华提出采用基于AHP的模糊综合评判方法对试题难度进行预估，并将该方法应用于大规模教育考试数学试题的难度预估和控制，取得了显著的成效[2]。王煜等人在CAT事前难度评定与综合难度评定的基础上，给出了事前综合难度的概念，建构了事前综合难度评定框架，并对2013年至2017年的全国高考数学Ⅱ卷（理科）试题进行了事前综合难度评定，拟合出预测事后难度的回归方程[20]。吕世虎等人在试卷相对难度和绝对难度的基础上提出了试卷综合难度的概念，结合中考数学试题，构建了6个要素刻画的数学试卷综合难度指标体系[21]。宋慧媛等人基于深度神经网络模型，利用试题文本信息，同时结合考生作答记录，建立试题文本信息与实际难度间的关联性，进而解决测试中试题难度参数的预估等问题[22]。

对于试题的整体分析，多从试题的整体考试范围、考试内容、试卷结构、整体难度、命题趋势、复习建议等方面进行综合分析，一般不会涉及测量理论或算法模型，研究者根据自己的经验对试题做出分析评判。黎郭凯对2017年美国SAT试题数学部分和全国高考理科乙卷试题，从试题形式、题量以及答题时间、试题考查内容、试题考查特点等方面进行对比分析，发现我国的高考试题在各个维度上都比SAT试题难度更高，但是SAT试题中丰富的现实情境素材、直观的图像表征方式和新颖的题型，以及试题与生活的紧密联系等都值得借鉴[23]。李志敏通过对比2016年全国新课标卷与广东卷数学试题在试卷结构、考试范围、题型、知识点考查等方面的差异，发现全国新课标I卷数学试题重视基础知识、突出重点知识、不忘“新增”内容和“边缘”知识，试题有机渗透了“函数方程思想”等多种思想，对学生的抽象与概括等多方面能力进行了全面的考查，作者在此研究基础上对高三数学复习提出了建议[24]。由于试题的整体分析不涉及复杂的测量理论或是算法模型，以经验判断为主，所以此类的文章作者多为一线教师。

试题难度的影响因素有多个方面，研究者对其水平的划分也有不同的标准，经过对文献的研读和整理，得到如图10所示的难度影响因素统计图。从总体来看，借鉴较多的是鲍建生教授的5因素难度模型，该模型提出影响数学试题难度的因素包括探究、背景、运算、推理、知识含量[5]。张怡等人在此基础上添加了是否含参、思维方向，使综合难度系数模型更加适应数学标准化试题的比较研究[25]。薛欢等人对武小鹏团队的综合难度模型进行调整，增加条件含量、阅读量（字符）两个因素，以凸显高考试题的命题变化[26]。李保臻等人认为高考数学解答题一般涉及到几个子问题，子问题之间是否有关联会影响试卷的综合难度，故而在武小鹏高考试题综合难度模型的基础上增加“梯度”因素[27]。吕世虎教授等人构建用试卷题型及其顺序、试卷题量与考试时间、试题难度分布、试卷阅读量、试卷新颖性、学生实际水平等6个要素刻画的数学试卷综合难度指标体系[21]。宋霜霜等人基于综合难度模型，以2015年至2020年大庆市中考数学试题为例进行研究，发现随着新课程改革的深入，背景类试题增多成为发展趋势，并根据这一变化规律为学生备考提出建议[28]。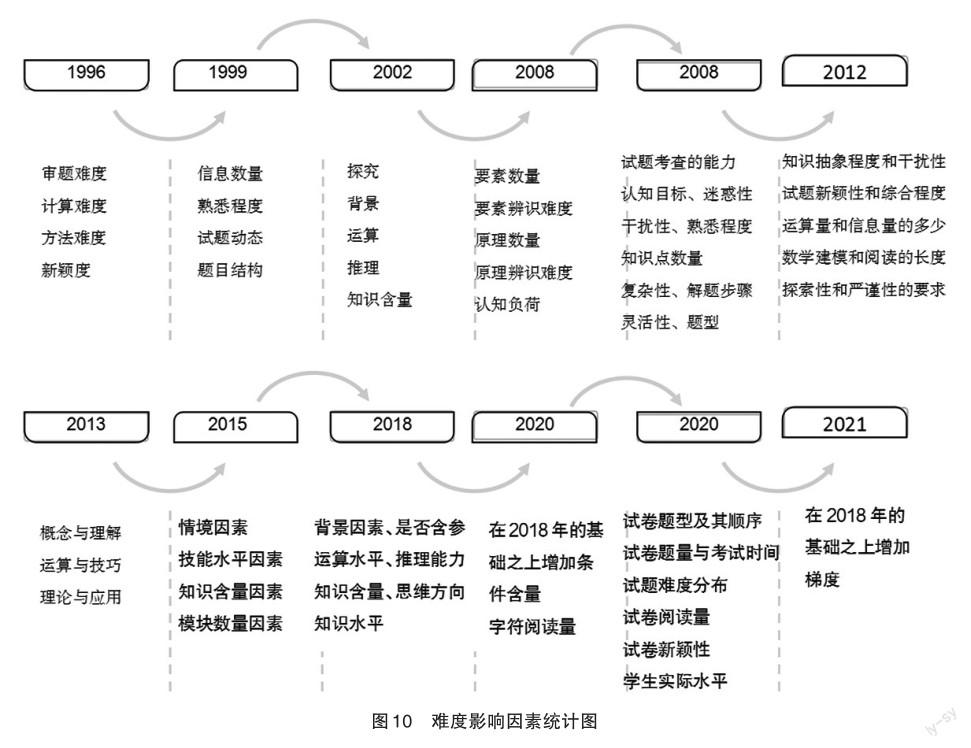

还有研究者从试题难度角度出发建立数学试题库。李捷等人研究了网络考试系统设计中利用遗传算法进行智能组卷的问题。针对试卷的难度指标，采用模糊数学方法和项目反应理论对试题库中每一小题进行综合评价试题难度的数学建模[29]。

文献综述的相关研究主要从试题难度的影响因素探讨，或是试题难度评估方法的发展方面进行综述。鲁庆云、宋乃庆2009年对我国数学试题难度影响因素进行研究综述，提出已有研究存在的问题，如提出的影响因素多基于思辨分析，缺乏实际数据支持，以及各因素对难度的贡献率有待商榷等[30]。罗玛等人对试题难度的影响因素和试题难度评估方法进行综述，发现难度评估方法正在向综合化、科学化发展[31]。

综合以上分析可以发现，目前国内关于数学试题难度的研究内容较为丰富，但是无论哪种研究都要回归研究的本质。之所以研究数学试题难度，其出发点是服务于教学和考试，而教学和考试又是培养和选拔人才的不同方式，归根结底，数学试题难度研究的最终落脚点要放在培养学生的能力和素养之上，这样的研究才是真正有意义的。

（六）难度评估方法分析

试题难度分为相对难度和绝对难度，对于相对难度的分析大多以经典测量理论和项目反应理论为理论基础，基于学生的实测成绩进行分析，而对于绝对难度的预估方法则多种多样，进一步整理文献得到如图11所示的难度评估方法统计图。周华辅利用影响试题难度因素的累积点换算得到试题的绝对难度[32]。毛竞飞运用命题教师主观评估、多元线性回归分析和BP神经网络建模三种预测方法，对高考命题过程中试题的难度进行预测，并对三种方法的预测性能进行比较，得出BP神经网络预测模型对试题难度的预侧准确度相对更高，误差相对更小[33]。王晓华利用AHP方法和模糊数学原理对命题专家的经验进行科学化总结和提炼，通过定性分析和定量分析相结合的方法对试题难度进行综合评判[2]。曾建国应用SOLO分类理论，从知识点考查的视角来评价高考数学试题[12]。王煜等人不仅给出了事前综合难度评定框架，还拟合出预测事后难度的回归方程，明确了事前、事后难度的关系[20]。佟威等人提出了分别基于卷积神经网络和循环神经网络的数学试题难度预测模型，以及二者的混合模型，以实现高效、准确的试题难度评估[34]。

如图11所示，研究者对数学难度模型的构建方法不断改进，其目的是使难度模型更加全面客观、科学合理。例如AHP虽然集合了众多专家的意见，但是主观性较强；多元线性回归虽然较为客观，但是假定影响因素与难度间呈线性关系，这是有待商榷的；BP神经网络算法很好地解决了非线性关系，但是这种算法的预测能力和训练能力有时会出现矛盾，即出现所谓的“过拟合”现象，导致预测能力下降。基于卷积神经网络和循环神经网络的数学试题难度预测模型，以及二者的混合模型，均直接对试题文本进行理解和语义表征，可保留试题描述的局部语义和语序信息，并且解决了不同考试中学生群体具有不可比性的问题，使得评价模型具有更好的性能[31]。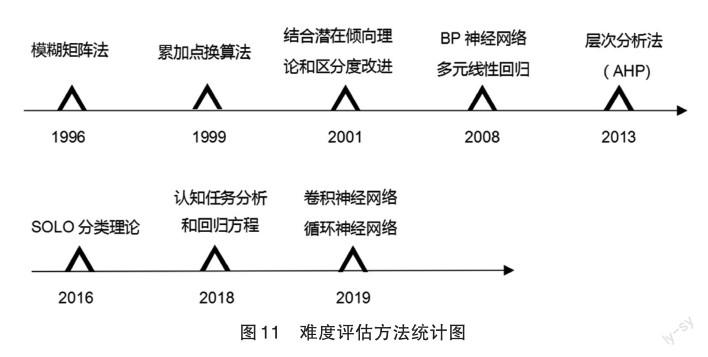

四、结论与展望

（一）研究结论

1.从研究趋势来看，国内对于数学试题难度的研究从2008年开始整体呈现递增的趋势，在2022年达到研究高潮，究其原因，与国家出台的教育政策紧密相关；研究对象以高考数学试题为主，义务教育阶段和高等教育阶段的数学试题难度研究较少。

2.從发表期刊和作者单位来看，国内发表关于数学试题难度研究的期刊较分散，载文量较少，发表于核心期刊的文献较少，相关研究的质量有待进一步提高。对于数学试题难度的研究绝大部分集中在高等院校，特别是师范类院校，各机构间的合作研究较少。从作者合著情况来看，以单人为主，其次是两人合作，多人合作的研究较少。

3.从研究热点来看，关键词集中在数学试题、高考数学、难度系数、高考数学试题、试题难度、综合难度模型、区分度、高考、综合难度。近几年研究的热点问题是综合难度系数模型、数学核心素养，采用较多的方法是比较研究。

4.从研究内容来看，关于数学试题难度的研究内容可以划分为六大类，分别是绝度难度、相对难度、二者结合、试题整体分析、影响因素、试题库研究。其中研究较多的是绝对难度，其次是试题整体分析，相对难度、二者结合与其他研究的文献数量持平，影响因素、试题库的研究较少。

5.从难度预评估方法来看，目前采用的评估方法包括经典测量理论、项目反应理论、SOLO分类理论、累积点换算法、层次分析法（AHP）、多元线性回归、BP神经网络算法、卷积神经网络算法、循环神经网络算法。

（二）展望

结合以上分析可以发现，目前国内关于数学试题难度的研究已经取得了一定成果，但在某些方面还有待进一步提高。

1.对义务教育阶段和大学阶段的数学试题难度研究有待加强。从相关文献来看，目前关于高考数学试题难度的研究较为丰富，这显然与高考的指挥棒作用密切相关，随着减负政策的落实及义务教育阶段新课标的颁布，相应学段数学试题的难度是否会发生一些变化？这还有待研究。

2.通过合著，提高研究质量。这里所说的合著包括两层含义，一是同单位间可以多人合作展开研究，二是不同单位间进行合作（高校、中小学、相关教研机构等）。通过整理文献发现，有24.19%的文献属于数学试题整体评析，即研究者只需要有一定的实践经验，就可以展开对试题内容、结构、特点等方面的评析。此类论文大部分只是凭经验给出关于试题难度的简单结论，缺乏客观数据的支撑，内容浅显，质量相对较低，参考价值较小。数学试题难度的研究若要有所突破，就必须深挖试题难度的本质，不仅要有定性的分析，更要定量与定性相结合。通过不同单位之间的协作，可以将理论、实践、大数据信息相互结合，这样才能透过现象看到本质，在相关领域获得突破。

3.研究内容还应更加丰富、多元。目前的相关研究多是从单独的试题难度出发，但是对于试题的评价远不止难度这一个指标，如区分度、信度、效度等指标，它们之间有着怎样的联系？能否通过难度有效预估区分度、信度、效度？目前对这些问题研究较少。另外，试题的评价还要符合时代的发展与要求，目前已经有研究者关注到将难度与数学核心素养结合，能够与教育政策紧密联系，这是一个很好的思路。当然也不止数学核心素养，随着高考评价体系的颁布，后期的相关研究还可以将高考评价体系作为试题难度研究的切入点。

4.预估算法应更加多样化、综合化。目前研究中用到的算法模型多是单个应用，但是每个算法其实都有其利弊，一种算法可能难以实现较好的预估效果，能否将不同算法的优势进行结合，使评价模型更为科学、合理？这还有待研究者继续探讨。

参考文献：

[1]国务院办公厅.关于新时代推进普通高中育人方式改革的指导意见[EB/OL].（2019–09–02）[2019–10–11].https：//zhuanlan. zhihu.com/p/80842215.

[2]王晓华.基于AHP的数学试题难度模糊综合评判[J].教育科学，2013，29（05）：38-43.

[3]郑程月.我国考试招生政策演进研究（1977—2017）[D].天津：天津师范大学，2018.

[4]王火生.高考制度改革的道與术——新中国高校招生考试制度改革历程的回顾与思考[J].教育学术月刊，2018，（02）：22-33.DOI：10.16477/j.cnki.issn1674-2311.2018.02.003.

[5]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002，31（09）：48-52.

[6]王建磐，鲍建生.高中数学教材中例题的综合难度的国际比较[J].全球教育展望，2014，43（08）：101-110.

[7]武小鹏，张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报，2018，27（03）：19-24+29.

[8]刘清，胡典顺，张莘钿.核心素养视角下的高考试题难度探析——以2019年高考数学全国卷（理科）为例[J].数学通报，2020，59（12）：34-40.

[9]王秋海.如何测量数学试题的难度[J].数学通报，1993，（07）：

26-27.

[10]林雪明.试题难度系数确定数学模型的建立与实现[J].杭州应用工程技术学院学报，2001，（01）：47-51.

[11]李二霞，邵志芳.试题难度多项指标的认知任务分析[J].心理科学，2009，32（06）：1342-1344+1317.DOI：10.16719/j.cnki.1671-6981.2009.06.058.

[12]曾建国.基于SOLO分类理论的高考数学试题评价研究——知识点考查的视角[J].赣南师范大学学报，2016，37（06）：130-134. DOI：10.13698/j.cnki.cn36-1346/c.2016.06.031.

[13]张碧霞，李琪，苏淑华，等.素养导向的数学试卷综合难度比较研究——以2018年高考全国卷Ⅰ、Ⅱ卷为例[J].科教导刊（上旬刊），2019，（19）：60-61.DOI：10.16400/j.cnki.kjdks.2019.07.027.

[14]张玉环，周侠.综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷[J].数学教育学报，2020，29（03）：43-50.

[15]韩金璇，杨泽恒，王彭德.中美高考数学试卷比较研究[J].数学教育学报，2022，31（02）：13-20+76.

[16]昌国良.新课程改革背景下高考数学题的教学导向[J].湖南师范大学教育科学学报，2007，（06）：29-30.

[17]李瑛.试测在高考命题试题难度调控中的实践研究[J].中国考试，2013，（03）：23 - 30. DOI：10.19360 / j. cnki. 11 -3303 / g4.2013.03.004.

[18]张天德，张召生，岳峰等.牢记立德树人教育使命助力数学教育和人才培养——2021年高考数学试卷分析与2022年高考新动向展望[J].中学数学杂志，2022，No.389（03）：26-32.

[19]周华辅.关于会考数学试题难度预估的实践与探讨[J].数学通报，1999，（02）：34-36+33.

[20]王煜，黄骁.全国高考数学试题事前综合难度分析研究[J].青海师范大学学报（自然科学版），2018，34（01）：1-5.DOI：10.16229/j. cnki.issn1001-7542.2018.01.001.

[21]吕世虎，于丽芳，王尚志.数学试卷综合难度的内涵及其指标体系建构[J].数学教育学报，2020，29（04）：1-6.

[22]宋慧媛，徐行健，孟繁军.基于题目关联知识的试题难度预测研究[J].内蒙古师范大学学报（自然科学汉文版），2022，51（03）：305-311.

[23]黎郭凯.2017年美国SAT试题数学部分与全国高考理科乙卷试题的比较分析[J].中学数学杂志，2018，（05）：28-30.

[24]李志敏.全国新课标卷与广东卷数学试题对比研究报告[J].中学数学研究（华南师范大学版），2016，（03）：25-30.

[25]张怡，武小鹏，彭乃霞.综合难度系数模型在2016年高考数学试题评价中的应用[J].教育测量与评价，2016，（12）：47-53.DOI：10.16518/j.cnki.emae.2016.12.009.

[26]薛欢，杜剑南，路江江.2016—2020年高考数学（理科）全国卷“统计与概率”试题探析——基于综合难度模型[J].教育测量与评价，2020，（12）：30-40.DOI：10.16518/j.cnki.emae.2020.12.005.

[27]李保臻，石烨.中国大陆与台湾地区高考数学试题难度比较研究——以2016—2018年大陆全国卷Ⅰ与台湾指考试题为例[J].数学教育学报，2020，29（01）：58-64.

[28]宋霜霜，陈建强.基于综合难度模型的中考数学试题背景分析——以2015—2020年大庆市中考数学试题为例[J].中学教学参考，2022，No.474（06）：34-36.

[29]李捷，吴玉田.智能组卷中的试题难度评价建模[J].肇庆学院学报，2012，33（05）：10-13.

[30]鲁庆云.我国高考数学试题难度影响因素的实证研究[D].重庆：西南大学，2009.

[31]罗玛，王祖浩.教育考试中试题难度的测评研究——影响因素、评估方法及启示[J].教育测量与评价，2016，（09）：52-57+64.DOI：10.16518/j.cnki.emae.2016.09.010.

[32]周华辅.关于会考数学试题难度预估的实践与探讨[J].数学通报，1999，（02）：34-36+33.

[33]毛競飞.高考命题中试题难度预测方法探索[J].教育科学，2008，24（06）：22-26.

[34]佟威，汪飞，刘淇，等.数据驱动的数学试题难度预测[J].计算机研究与发展，2019，56（05）：1007-1019.

Literature Review on the Difficulty of Mathematics Questions in China

Yang Congcong Yan Fang

School of Mathematics，Yunnan Normal University，Kunming，Yunnan，650500

Abstract：With the help of VOSviewer software，this paper sorts out and summarizes the domestic literature on the difficulty of mathematics questions. 130 pieces of journal literature are collected and screened from the CNKI database，and analyzed from six dimensions：journal source，age distribution，author status，keyword distribution，research content and evaluation method. It is found that the research is on the rise in general，but the journals are scattered，the number of published papers is small，and there are few core journal literature. In recent years，the method of comparative research has been used to study hot issues such as comprehensive difficulty coefficient model and mathematical core literacy. In view of this，some suggestions are put forward for the future research direction，such as strengthening the research on the difficulty of mathematics questions in compulsory education and higher education，improving the quality of the research through co-authorship，and making the research content and prediction method more diversified.

Key words：Difficulty of Mathematics Questions，Comprehensive Difficulty，Content Analysis Method

（责任编辑：吴茳）