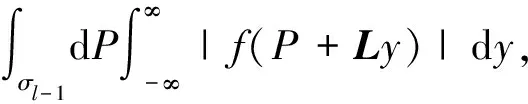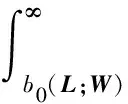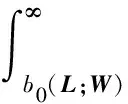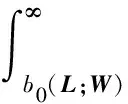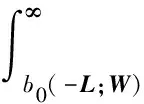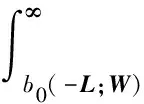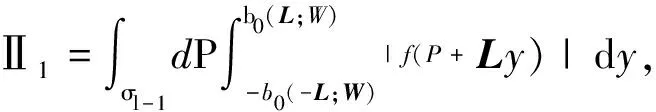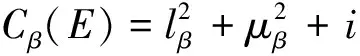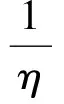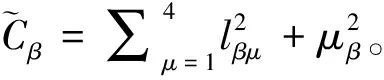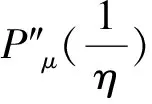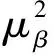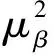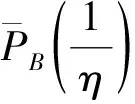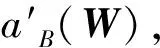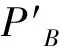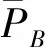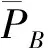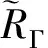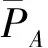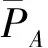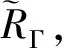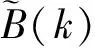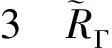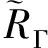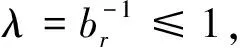BPHZ重整化的收敛与温伯格渐进定理
要宏佳,郝 昆,杨战营,杨文力,石康杰
(1.西北大学 现代物理研究所,陕西 西安 710127;2.西北大学 物理学院, 陕西 西安 710127)
粒子之间的相互作用可以用费曼图[1-3]表示。这些图的外线代表入射粒子和出射粒子,内线代表费曼传播子,费曼图Γ给定后,可以计算它的值SΓ。当费曼图没有回路时,可以直接计算粒子之间的散射振幅,有回路时必须对回路对应的动量积分。这种积分通常是发散的,这就需要在拉格朗日密度中添加抵消项来抵消这种发散。扣除抵消项(A)后得到
RΓ=SΓ-A,
(1)
RΓ在动量空间的积分就是收敛的[1,4-9]。
这种抵消发散的方法可以作如下解释,原始的物理量是发散的不可测量的,我们测量到的结果是各种粒子相互作用之后的结果,也就是那些发散量由于相互作用抵消的结果,这些量包括相互作用常数。这些量是有限的,这样做就等于给物理量重新进行标度,所以叫做重整化[3,10-11](renormalization)。
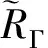
(2)

1 温伯格渐近定理及An类函数
下面介绍温伯格渐近定理。
首先定义动量空间Rn中的An类函数,实函数f(P)称为属于An。如果对每个子空间S⊂Rn有对应的“指数”α(S)和“对数指数”β(S),而且对任何m≤n个独立矢量(L1,L2,…,Lm)和Rn中的有界区域W(W是n维),存在一系列实数b1,b2,…,bm>1和M>0(它们依赖于L1,L2,…,Lm与W,但与η1,η2,…,ηm无关)使
|f(P)|=|f(L1η1…ηm+L2η2…ηm+…+
Lmηm+C)|≤
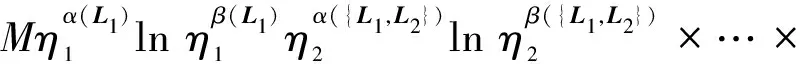
(3)
当C∈W且η1≥b1,η2≥b2,…,ηm≥bm时成立。
因此:
M=M(L1,L2,…,Lm;W);
(4)
bl=bl(L1,L2,…,Lm;W)>1。
(5)
为了方便,我们要求当任何几个坐标矢Li反号时,M和bl不变:
M=M(±L1,±L2,…,±Lm;W);
(6)
bl=bl(±L1,±L2,…,±Lm;W)。
(7)
令P=L1η1η2…ηm+L2η2…ηm+…+Lmηm+C,我们称满足条件
C∈W,|ηi|≥bi(L1,L2,…,Lm;W)
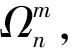
要强调的是,当C在W内变化时,FW是不变的。现在考虑f(P)的积分
(8)

(9)


由Fubini定理可知,这两者相等。为了方便,可以选一些子空间E,满足
Rn=I+E。
(10)
I和E相互独立,并且把P局限在E内。
温伯格导出如下定理。
定理1
如果①函数f(P)∈An其渐近指数为α(S)、β(S),其中,S是任何Rn的非空的子空间。并且如果②f(P)在任何Rn的有界区域σ绝对可积,
(11)
且如果③DI<0,
其中
(12)
则有以下结果:
1)fI(P)存在;
2)fI(P)∈An-k,其αI(S)对任何S⊂E由下式给出,
(13)
式中:S′⊂I表示S′是I的子空间,包括S′=I;dimS′表示S′的维数;Λ(I)S′=S表示S′沿I向E的投影是S;max表示取所有满足Λ(I)S′=S的S′,对这样的S′取极大值。实际上,根据Heine-Borel定理,在下一节证明只有有限个S′需要考虑,所以这里的max是对有限个量取最大值。
式(13)的右边一般不是空间S的函数,因为式(13)中α(S′)+dimS′不是一个确定的数。本文令α({S})=-dimS-1,
β({S})=β≥0。
(14)
β与S无关,就可以保证式(13)成立。
式(8)是一个多重积分,只要把每一个单重积分研究清楚就可以了,因为它们都是-∞到+∞的积分,各重积分被积函数的结构相同。下一节研究单重积分,它是渐近定理的关键或实质部分。
2 渐近定理证明的关键部分
考虑I={L}以及

(15)
式中:f∈An。按式(3)、(6)、(7)、(14),当P∈W,
|y|≥b0(L;W),有
|f(P+Ly)|≤M(L;W)|y|α(L)ln|y|β(L)。
(16)
由于非空的I={L}的子空间只有I(={L})自己,式(12)给出DI=α(L)+1。根据式(14),
α(L)=-2<-1。
(17)
由此,式(15)中|y|≥b0的两段积分绝对收敛。另一方面,|y|≤b0的区间是有界的。根据式(11),f在这段的积分也绝对收敛。因此对任何P,fL(P)存在,渐近定理1的第1)部分成立。令P点在E上,证明了对E上的任何点P,fL(P)存在。
下面证明定理1的第2)部分。
任选矢量序列L1,L2,…,Lm∈E,它们之间以及它们和L之间互相独立;选定Rn中的有界区域W。我们的任务是证明若f∈An,并满足式(11)、(14),则fL(P)∈An-1。换句话说就是可以找到M(L1,L2,…,Lm;W)和bl(L1,L2,…,Lm;W),当ηl≥bl,C∈W,
就有
(18)
式中
P=L1η1…ηm+L2η2…ηm+…+Lmηm+C。
(19)
我们还须证明式(13)。
为了用f∈An的性质求式(15)的渐近覆盖,首先把y写成
y=ξ0η1η2…ηm。
(20)
令|ξ0|=η0,y=±η0η1…ηm,得到
P+Ly=L1η1…ηm+L2η2…ηm+…+Lmηm+C±Lη0η1…ηm=±Lη0η1…ηm+L1η1…ηm+…+Lmηm+C。
(21)
这正是在坐标系{±L,L1,…,Lm;W}下,P+Ly的η参数化。对比式(3),由于f∈An,有:
bl=bl(±L,L1,…,Lm;W)>1;
(22)
M=M(±L,L1,…,Lm;W)。
(23)
由式(6)、(7)和式(22)、(23)右边对于+L和-L相等,当C∈W,ηl≥bl,l=0,1,…,m,有:
|f(P+Ly)|≤
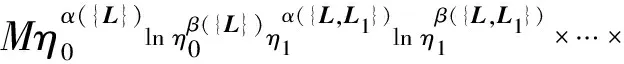
(24)
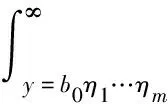
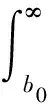

(25)
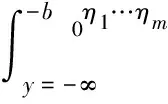
(26)
在这一段
ξ0≤-b0η1…ηm,η0≥b0η1…ηm。
(27)
因此有
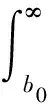

(28)
我们计算式(27)、(28),由式(14)、(24)根据各η相关空间的维数得
(29)
其中
(30)
当Li中有任意一些Lj反号变为-Lj时,由式(7)可得,bl和M不变,因为α和β的宗量是这些矢量形成的空间,不会因为某几个Lj反号而改变空间,因而α和β的宗量也不变,所以FW不变,而且N=N(α{L},β{L})也不变。
在y=-∞→∞中间有一段
y∈[-b0,b0]η1η2…ηm,
(31)
对应ξ0∈[-b0,b0]不符合η0=|ξ0|≥b0条件,须另作处理。
我们用中点为u,半径为λ的小开区间(u-λ,u+λ)覆盖闭区间[-b0,b0]的u点,这总是可能的。
令
Δξ1∈(u-λ,u+λ),
(32)
由式(31)可得
y=(u+Δξ1)η1…ηm;
(33)
令
(34)
有
y=uη1η2…ηm+ξ1η2η3…ηm;
(35)
再令
(36)
得
(37)
由式(19)的P给出
Lη0η2…ηm+L2η2…ηm+…+Lmηm+C。
(38)
这正是在坐标系{L1+uL,±L,L2,…,Lm;W}下P+Ly的η参数表达式。由于f∈An,有:
bl(u)≡bl(L1+uL,±L,L2,…,Lm;W)>1;
(39)
M(u)≡M(L1+uL,±L,L2,…,Lm;W)。
(40)
由式(6)、(7)可知,式(39)、(40)的右边与±号无关。根据式(38)中各个η相关的空间维数和式(14)得到如下结果。
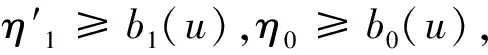
(41)
有
(42)
令
(43)
这样,闭区间[-b0,b0]上每一点u都被小开区间(u-λ(u),u+λ(u))覆盖。由Heine Borel定理可知,其中一定存在有限个小开区间(ui1-λ(ui1),ui1+λ(ui1))写成(ui1-λi1,ui1+λi1),i1=1,2,…,S,交迭在一起也可以覆盖整个闭区间[-b0,b0]。
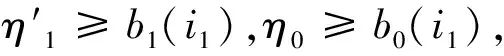
ηl≥bl(i1)
(44)
时,有
(45)

(46)
I+i1≤

(47)

(48)
得到
(49)
由于式(45)中FW(i1)对ξ1的依赖关系只与其绝对值有关,我们有I-i1 (50) (51) Δξ2η2=ξ2, (52) 有 y=ui1η1…ηm+uη2…ηm+ξ2η3…ηm (53) 和 P+Ly=L1η1…ηm+L2η2…ηm+…+Lmηm+C+L(ui1η1…ηm+uη2…ηm+ξ2η3…ηm)= (L1+ui1L)η1…ηm+(L2+uL)η2…ηm+Lξ2η3…ηm+L3η3…ηm+…+Lmηm+C。 (54) (55) 和 (56) 这正是在坐标系{L1+ui1L,L2+uL,±L,L3,…,Lm;W}下P+Ly的η展开式。由于f(P+Ly)∈An,就有 bl(i1u)≡bl(L1+ui1L,L2+uL,±L,L3,…,Lm;W)>1,l=1,2,0,3,…,m (57) M(i1u)≡M(L1+ui1L,L2+uL,±L,L3,…,Lm;W)。 (58) 根据式(6)和(7)可得,二者对±L的值相同。根据式(56)中各个η涉及的空间维数和式(14), ηl≥bl(i1u), (59) 有 |f(P+Ly)|≤ (60) 对于小区间(ui1i2-λi1i2,ui1i2+λi1i2),改写M和bl的符号M(i1u)→M(i1i2),bl(i1u)→bl(i1i2),改写式(60)中 FW(i1u)→FW(i1i2)。 (61) (62) 由式(53)可得 y=ui1η1…ηm+ui1i2η2…ηm+ξ2η3…ηm。 (63) 因此,当ξ2>0,有 (64) (65) 由于FW(i1i2)只与ξ2的绝对值|ξ2|有关。式(65)的右边等于 (66) 由式(62)、(64)得到: (67) N′(i1i2)= (68) 由式(64)、(66)得 J-i1i2=J+i1i2= (69) 然而|ξ2|≤b0(i1i2), 即ξ2∈[-b0(i1i2),b0(i1i2)]的区域没有渐近覆盖。我们用中心在u,半径为λ的小开区间(u-λ,u+λ)覆盖闭区间[-b0(i1i2),b0(i1i2)],在这小开区间的变量为Δξ3,ξ2=u+Δξ3,ξ2与y的关系是式(63),可得这过程可以一直进行下去。到第r步时,要处理ξr-1∈[-b0(i1…ir-1),b0(i1…,ir-1)]这段闭区间的问题。ξr-1与y的关系是 y=ui1η1…ηm+…+ui1…ir-1ηr-1…ηm+ξr-1ηr…ηm, (70) 用小开区间(u-λ,u+λ)覆盖闭区间[-b0(i1…ir-1),b0(i1…ir-1)]的u点。令小开区间内 ξr-1=u+Δξr, (71) 也就是 y=ui1η1…ηm+…+ui1…ir-1ηr-1…ηm+(u+Δξr)ηr…ηm, (72) 导出 P+Ly=L1η1…ηm+…+Lmηm+C+ L(ui1η1…ηm+…+ui1…ir-1ηr-1…ηm+(u+Δξr)ηr…ηm)=(L1+ui1L)η1…ηm+…+(Lr-1+ui1…ir-1L)ηr-1…ηm+(Lr+(u+Δξr)L)ηr…ηm+Lr+1ηr+1…ηm+Lmηm+C。 (73) 令Δξrηr=ξr, (74) 得到 P+Ly=(L1+ui1L)η1…ηm+…+(Lr-1+ui1…ir-1L)ηr-1…ηm+(Lr+uL)ηr…ηm+Lξrηr+1…ηm+Lr+1ηr+1…ηm+…+Lmηm+C。 (75) 根据式(74),令 |ξr|=η0, (76) ηm±Lη0ηr+1…ηm+Lr+1ηr+1…ηm+…+Lmηm+C。 (77) 根据式(14)和式(77)中各个η相关空间的维数,有 (78) 命题1由于闭区间[-b0(i1…ir),b0(i1…ir)]的中点为0,所以开区间集合(-ui1…ir-λi1…ir,-ui1…ir+λi1…ir),ir=1,2,…,Sr也能覆盖[-b0(i1…ir-1),b0(i1…ir-1)]在这些小区间中的一个,我们标志: bl(i1…ir-1u)|u=ui1…ir≡bl(i1…ir); (79) M(i1…ir-1u)|u=ui1…ir≡M(i1…ir); (80) FW(i1…ir-1u)|u=ui1…ir≡FW(i1,…ir)。 (81) y=ui1η1…ηm+…+ui1…ir-1ηr-1…ηm+ ui1…irηr…ηm+ξrηr+1…ηm。 (82) 给出I±i1…ir: |f(P+Ly)|dy≤ (83) |f(P+Ly)|dy≤ (84) 由于命题1对所有的r都适用(r=0,1,…,m),我们有如下命题。 命题2当Lj中有一些反向,Lj→-Lj令伴随的ui1…ij→-ui1…ij,Lj+ui1…ij→-(Lj+ui1…ijL),这时由式(6)和(7)可得,bl(i1…ir)不变,M(i1…ir)不变,又由于式(13)可得,α、β也不变,最终使渐近覆盖函数FW(i1…ir)不变,因而J±i1…ir不变。 将式(74)、(76)代入式(78)、(81)得 |f(P+Ly)|≤FW(i1…ir)= (ηr/|ξr|)-r-1×ln(ηr/|ξr|)β× (85) 由式(82)、(83)得 (86) I±i1…ir (87) (88) N′(i1…im)= N(i1…im),ξ=ξm (89) 得到 (90) 我们有如下命题。 命题3由命题2取r=m有,当Lj中有一些反向,J±i1…im不变,b0(i1…im)不变。 现在我们还留下ξm∈[-b0(i1…im),b0(i1…im)],y=ui1η1…ηm+…+ui1…imηm+ξm这一段须处理。对这一段有 P+Ly=L1η1…ηm+…+Lmηm+C+ L(ui1η1…ηm+…+ui1…imηm+ξm)= (L1+ui1L)η1…ηm+…+ (Lm+ui1…imL)ηm+Lξm+C。 (91) 找一个W′,使当C∈W时,Lξm+C∈W′。符合条件的最小的W′是W⊗L[-b0(i1…im),b0(i1…im)]。它的构成是把W中的每一点扩张为以该点为中点的线段L[-b0(i1…im),b0(i1…im)]。这样,当ξm∈[-b0(i1…im),b0(i1…im)],Lξm+C一定∈W′。由命题3有当Lj中有一些反向为-Lj时,也有b0(i1…im)不变。 令C′=Lzm+C∈W′,有 P+Ly=(L1+ui1L)η1…ηm+…+ (Lm+ui1…imL)ηm+C′。 (92) (93) 得到 I0i1…im= (94) 如果Lj中有一些反向Lj→-Lj,伴随的ui1…ij也同时反号ui1…ij→-ui1…ij,则Lj+ui1…ijL→-(Lj+ui1…ijL),由于W′=W⊗L[-b0(i1…im),b0(i1…im)],由命题3可得,b0(i1…im)不变,所以W′不变,坐标系变为 {±(L1+ui1L),±(L2+ui1i2L),…,±(Lm+ui1…imL);W′}。 命题4当Lj中的某一些反号,且式(6)和(7)成立时,所有J±,J±i1…ir,J0i1…im都可以做到不变。所以式(6)和(7)可以由Rn递推到Rn-1。 |fL(P)|,已经知道的结果是,当 ηl≥max{bl},l=1,2,…,m, (95) (96) 所以有 (97) (98) 我们计算了J±,J±i1…ir,J0i1…im,由它们给出了在Rn-1=E上An-1函数fL(P)的渐近覆盖。令P=L1η1…ηm+…+Lmηm+C,有 (99) (100) (101) N2=1(取式(14)时,由附录A给出); 2b0(L1+ui1L1,…,Lm+ui1…imL;W); (102) W′=W⊗[-b0(i1…im),b0(i1…im)]L; (103) bl(L1+ui1L,…,Lr+ui1…irL,Lr+1,…, W′)}; (104) αi=-i-1,βi=2β+1。 (105) 式(14)成立。式(104)中右边的e是为了使lnη≥1。 另一点要说明的是在对各个J中沿L方向积分时,矢量C=Cn-1,W=Wn-1都不变。对于J0i1…im,C∈W⊂W′不变,因为J(P)的P不变,对J0i1…im,ξ沿L方向从-b0(i1…im)积到b0(i1…im),中点是矢量C的端点,保持在W′内积分时,Ly沿L方向的投影总是在P点不动。 我们有如下定理。 定理2当fn∈An,而且对于任何坐标系有式(14)时,可以由温伯格程序给出Rn-1任何坐标系的 (106) 这里还有一个重要细节须说明,在式(83)中当积分J±i1…ir时,ηr必须大于b0(i1…ir)br(i1…ir),否则这项就不存在。而对于其余ηr′≠r,则只要求ηr′≥br′(i1…ir),为解决此问题,温伯格引入新参量C(i1…ir)。本文改为全部要求ηr≥br(i1…ir),理由是渐近覆盖FW的值可以任意扩大,只要是有限值,就不影响理论框架。从式(99)来看,我们这样处理,就是当b0(i1…ir)br(i1…ir)≥ηr≥br(i1…ir)时,多加了一项本来不存在的有限项,这时Mn-1本来没有式(100)~(102)联合给出的那么大,我们的处理方式只是使它变大了而已,好处是使式(104)简单了。其实我们在很多计算比如由式(86)给出式(87)时,就曾经一再扩大积分的值(见附录A)。在这些处理中,我们只是把“=0”扩大为“>0”,把“小”的值扩大为“大”的值。不违背渐近覆盖式(99)是“有限的”这个原则,因此也是允许的。 下面我们的问题是要从Rn的An函数fn积到Rn-k的An-k函数fn-k(P)我们还需要什么。我们只需要在Rn-k+1的对应An-k+1函数fn-k+1在有界线段上绝对可积,这个条件又如何保证呢?下面的推导表明这只要对应的fn-k+2在二维平面的有界区上绝对可积。最终,我们发现当fn∈An对1维至n维平面的有界区域绝对可积,而且α({S})=-dimS-1,βS≥0与S无关,fn就在整个k空间绝对可积。其中,积分的每一步都需要这两条性质递推下去。第2节的式(104)、(105)给出α和β的递推性质,第3节我们推导在有界区域绝对可积条件式(11)的递推性质。 命题5如果fl∈Al在Rl的任何1~l维平面区域σl绝对可积,而且αl({S})=-dimS-1,则其积分函数fL(P)在E=Rl-1上的任何1~l-1维平面上的有界区域σl-1绝对可积。 注意:σl是1~l维平面上的有界区,是边缘光滑,在勒贝格积分意义下的可测点集。我们只用到各维的平行多边形, σl=Lmkm⊗…⊗Lm-ikm-i, i=0→l,kS≡(aS,bS)。 (107) 式中:kS是线段。由式(83)、(84)可得,fL(P)的覆盖函数FW的α、β指数满足式(14)。下面证明fL(P)在任何E=Rl-1上的任何1~l-1维边缘光滑的σl-1绝对可积。 (108) (109) (110) (111) (112) (113) 当α<-1时收敛。 (114) 当α(-L)<-1时收敛。 因为W⊃σl-1,所以对于任何P∈σl-1,参量M、b0都与P无关。α和β也只与L、-L有关,因而与P(相当于式(3)中的C)无关。 Ⅱ1+Ⅱ2+Ⅱ3, (115) 其中 (116) 有界,Ⅱ3也类似。 命题6如果Al函数在Rl的任何有界区σl的积分绝对收敛,则由温伯格程序得到的Rl-1的Al-1函数在Rl-1的任何有界区σl-1的积分也绝对收敛。 B(k)=ΠβCβ(E), (117) (118) 有 (119) 式中: (120) 我们定义 (121) (122) dσ是σ的面积元。k空间的任何线性函数f可以表为一个矢量a与k空间的矢量P的内积a·P。对于k空间的超平面T, P=L1k1+L2k2+…+Lmkm+C= L1η1η2…ηm+L2η2…ηm+…+ Lmηm+C。 (123) 式中:C∈W,W是Rn的有界区,有 f=f1η1η2…ηm+f2η2…ηm+…+fmηm+f0, (124) f0=a·C,fi=a·Li,i=1,2,…,m。 (125) 1)当f1,…,fm中有非零值的时候,排在最前面的非零项fkηk…ηm在η充分大时变为主要项, (126) 2)当所有fi(i=1,2,…,m)都为0时, f=f0=a·C (127) 是C的线性式。 1)当对于β,有至少一个μ,有式(126)中f≠0,且对所有μ,fi=0,i=1,2,…,k-1。由于lβμ是k的线性项[15],根据式(126), (128) (129) ji(β)=0,i=1,2,…,k-1, ji(β)=2,i=k,k+1, …,m。 (130) 2)当对于β,对所有的μ,有fk=0,k=1,2,…,m,这时 (131) 式中:aβ是C和q以及μβ的大于0的二次式。 j1(β)=…=jm(β)=0 (132) (133) (134) 则有 (135) (136) |di(C)|≤di(W)。 (137) bl(L1,L2,…,Lm,W)≥e (138) 使当 |ηl|≥bl (139) 有: (140) (141) 我们有 (142) 根据文献[15],A(k)是kq的多项式,而k可以按式(123)~(127)展开,这样A(k)就可以展开为η的多项式, A=QA(η), (143) 取各项中ηl的最高幂次加以比较,可以找到所有项的η的最高幂次sl,然后把QA(η)写成 (144) (145) 当我们令 |ηl|≥bl(L1,L2,…,Lm;W)≥e, (146) (147) |A|≤|η1|s1…|ηm|smP(A)。 (148) 由式(143)和式(148)得如下命题。 命题8 (149) 由命题7和8有如下命题。 M=M(±L1,±L2,…,±Lm;W); bl=bl(±L1,±L2,…,±Lm;W)。 令ki…km都不为0, ki≠0,i=1, …,m, (150) 等价地有 ηi≠0,i=1, …,m。 (151) Tl平面是在式(150)条件下取kl+1,…,km为固定值形成的平面(或等价地在式(151)前提下将ηl+1…ηm固定形成的平面)。 令k的多项式(已合并同类项)为 (152) Q在T的幂次为 (153) Q在Tl的幂次为 (154) 我们将 k1=η1…ηm,k2=η2…ηm,…,km=ηm 代入式(154)得 (155) Q对ηm的幂次为 (156) Q对ηl的幂次为 (157) 对比式(153)和(155),式(154)和(157),我们发现 degkQ(k)|T=degηmQ(k(η)), (158) degkQ(k)|Tl=degηlQ(k(η)), (159) 这是同一个Q(k(η))! (160) (161) 我们有 (162) sl-jl=αl<-l。 (163) αl=-l-1,βl=0。 (164) 我们有如下定理。 证明令Rn=L1y1⊗L2y2…⊗Lnyn,yi=-∞→∞。然后顺次沿L1…Ln方向积分,每次都可保证式(14)、(6)、(7)和有界平面区绝对可积条件式(11)直至R1的A1函数。由式(14)和式(11)可知,在Ln方向也绝对可积。 附录A (165) 式中: (166) (167) (168)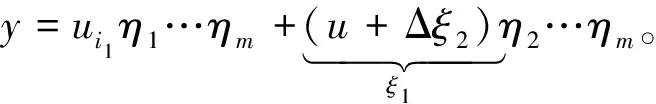
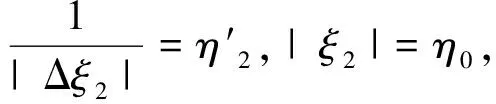

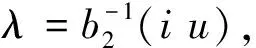
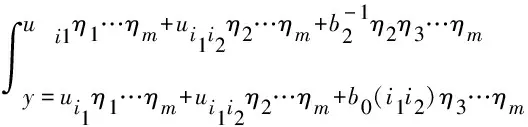
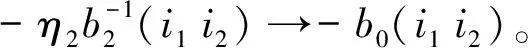
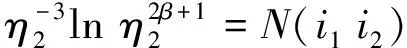

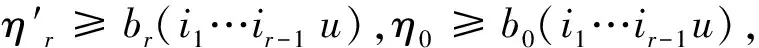

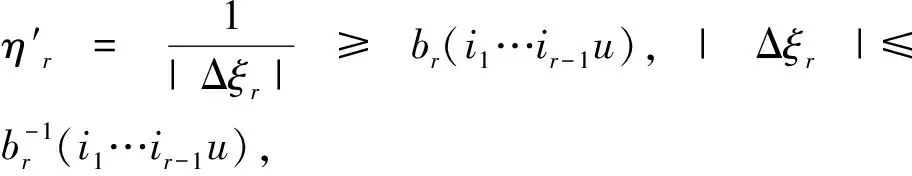
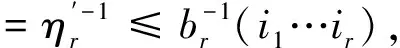
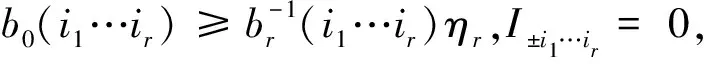
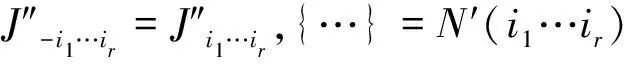
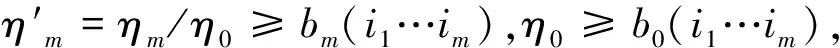
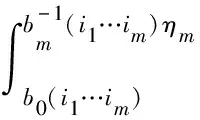
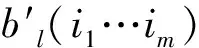
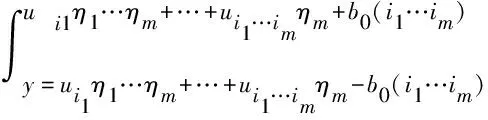

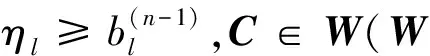
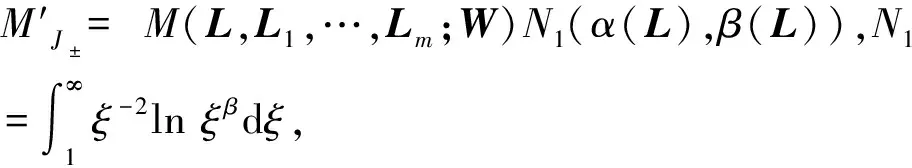
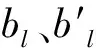

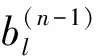
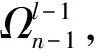

3 f在有界区绝对可积的分析