利用高阶累积量相关性的地震波传感器阵列目标检测方法

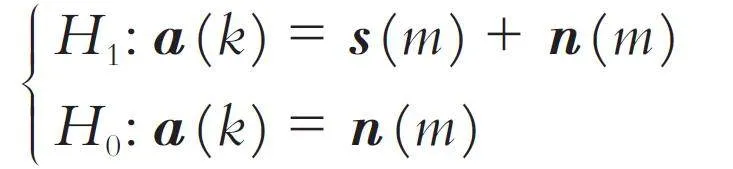
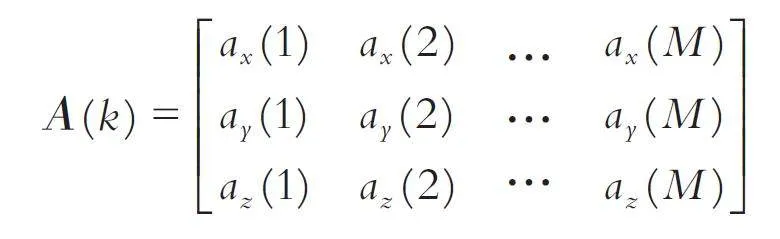
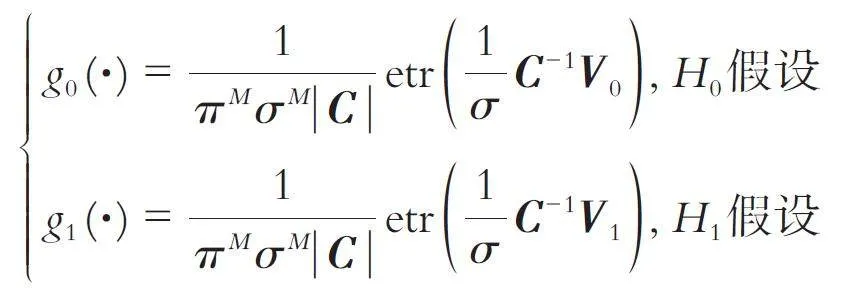
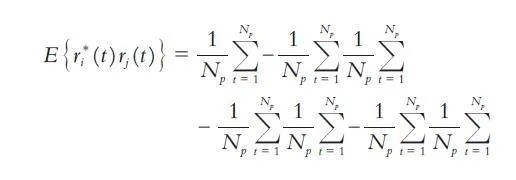
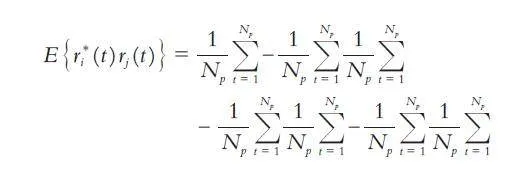
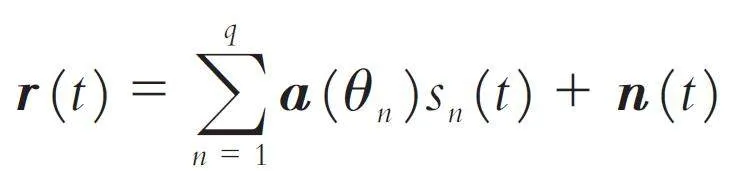
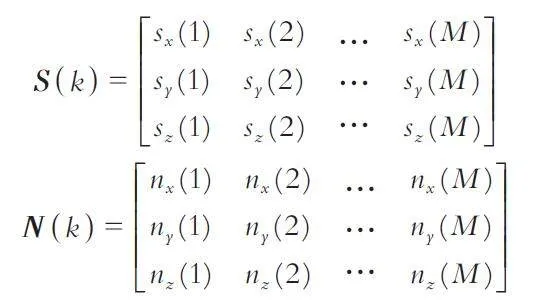
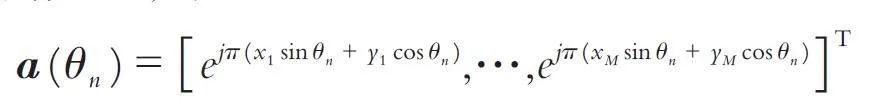
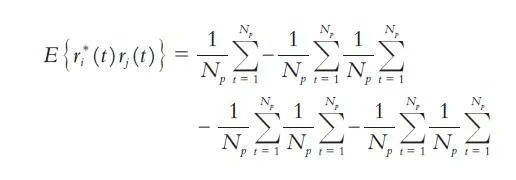
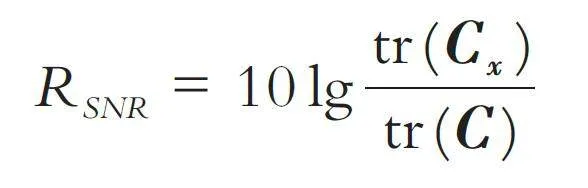
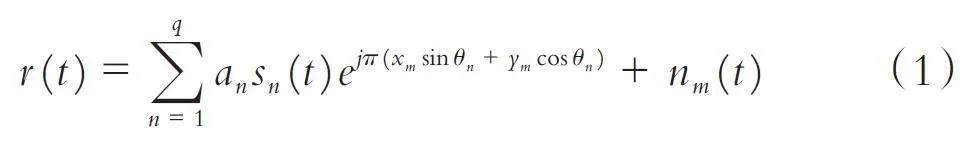
摘 要：针对传统决策级判决检测方法虚警率高、信息浪费的问题，提出一种远场环境下可有效消除噪声影响的基于高阶累积量矩阵相关性目标检测方法：通过在传感器节点端设定一个发送数据的触发门限，预先对参与融合检测的传感器节点个数进行约束，融合中心在收到节点发送的数据后，计算信号的四阶累积量构建累积量矩阵，并构建相关性统计量作为融合检测的判决统计量；利用临近节点信号累积量矩阵列向量之间的相关性，结合判决统计量得到在恒虚警概率下的检测门限，判断目标是否存在，实现对目标的融合检测. 仿真发现其在不同噪声环境下能有效检测出目标，且检测性能优于现有检测方法.

关键词：高阶累积量；相关性；融合检测；传感器阵列

中图分类号：TN911.7

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.07

利用多传感器进行融合检测按照融合级别的不同分为信号级融合检测和决策级融合检测[1]. 信号级融合检测方法在分布式的传感器节点完成数据采集后，不进行数据处理或只作简单处理，将采集信息传输到融合中心后进行全局数据处理并优化决策.决策级融合检测是由本地传感器节点先对目标进行检测，获得检测结果后将决策结果等少量信息发送到融合中心，只利用多节点的检测结果进行综合检测[2]. 传统决策级判决检测优势在于最大化减少传感器之间的数据通信量，适用于对通信开销要求严格的环境，如水下无线声通信网络；缺点是未考虑单个节点的检测可能会受噪声干扰严重存在虚警，且忽略了在对相同目标进行检测时传感器节点之间采集数据的相关性，造成信息浪费[3-4].

针对水下无线地震波传感器阵列特点，本文提出一种基于高阶累积量矩阵相关性的目标检测方法. 传统阵列信号处理技术一般仅使用信号的二阶统计特征值，在高斯条件下，信号的二阶统计特性确定已知，且信号可由二阶特征值准确描述. 但在实际应用环境中，远场信号源会产生非高斯信号，这时信号的特性就不能由二阶统计量进行准确描述，需要研究信号的高阶累积量[5]（higher order cumu⁃lants）.考虑到部分节点距离目标较远或处在信号较弱位置，接收信号中目标成分很弱，若每次融合检测均接收所有节点数据，反而会降低总的检测概率[6].因此，预先对参与融合检测的传感器节点个数进行约束. 在传感器节点端，给节点设定一个发送数据的触发门限，针对水下地震波传感器阵列特点和节点工作特性，选择预设触发门限. 融合中心在收到传感器节点发送的数据后，计算信号的四阶累积量，构建累积量矩阵. 若目标存在，则临近节点接收信号的累积量之间具有相关性，即累积量矩阵列向量之间具有相关特性，利用累积量矩阵的不同列向量计算传感器接收信号之间的相关性，构建相关性统计量作为融合检测的判决统计量. 根据节点接收的信号特点计算检测概率和虚警率，结合判决统计量得到在恒虚警概率下的检测门限，实现对目标的融合检测.

1 高阶累积量信号处理模型

1.1 信号高阶累积量

高阶累积量是利用信号的高阶统计特性，能够完全抑制任何高斯噪声. 比较常用的高阶累积量包括三阶累积量和四阶累积量，其中在满足Laplace、线性或高斯对称分布的随机过程中，信号的三阶累计量值为零，另外多数情况下信号三阶累积量值很小而四阶累积量值较大，利于估计信号特性. 同时，大量文献[7-8]已经证明高阶累积量具有更精细的描述信号能力，可以用来解决一些更复杂的信号处理问题. 高阶累积量的运算特性主要包括：

对随机变量{ xi }ni= 1 和常量{ ai }ni= 1，有

cum （a1 x1，a2 x2，…，an xn ） （ Πi = 1nai） "cum （x1，x2，…，xn ）

对随机变量{ xi }ni= 1 和y1，有

cum （x1 + y1，x2，…，xn ）= cum （x1，x2，…，xn ） + cum （y1，x2，…，xn ）

对相互独立的随机变量{ xi }ni= 1 和{ yi }ni= 1，有

cum （x1 + y1，x2 + y2，…，xn + yn ）= cum （x1，x2，…，xn ） + cum （y1，y2，…，yn ）

信号高阶累积量具有抑制任意协方差高斯噪声的能力. 即对于随机变量{ xi }ni= 1 和独立高斯随机变量{ zi }ni= 1，有

cum （x1 + z1，x2 + z2，…，xn + zn ）= cum （x1，x2，…，xn ）

如果存在随机变量子集{ xi }ni= 1 与集合其他部分相独立，则

cum （x1，x2，…，xn ） = 0

以上运算中随机变量的排序不会影响运算结果. 对于四阶累积量，其定义为

cum （xi，xj，xk，xl ）= E { xi，xj，xk，xl } - E { xi xj } E { xk xl }-E { xi xk } E { xj xl } - E { xi xl } E { xj xk }

1.2 信号处理模型

假设不规则阵列由M 个阵元构成，阵元相对位置随机. 有q 个球面波窄带信号入射到阵列上，入射信号满足零均值高斯分布，中心频率为w0，入射角度分别为{ θ1，θ2，…，θq }. 则第m 个传感器节点接收到的信号可表示为

其中：sn （t ） 为第n 个来波的入射信号，a n 为传感器节点对第n 个来波的响应系数，（xm，ym ）为第m 个阵元的二维坐标位置，nm （t ） 为在第m 个阵元上的加性高斯噪声，假设其方差为σ2 且与信号sn （t ） 独立，不同节点接收噪声之间亦独立. 若不同节点之间具有全向单位增益，即an ≡ 1，则式（1）可用矢量表示为

其中： r （t ），n （t ） 为M × 1 维向量r （t ） [ r1 （t ），…，rM （t ） ]T、n （t ） [ n1 （t ），…，nM （t ） ]T，a （θn ）为阵列在入射角度θn 上的导向矢量，即

进一步简化阵列接收信号模型，有

r （t ） = A（θ ）S （t ） + n （t ）

式中： S （t ） 为q × 1 维的信号矢量S （t ） = [ s1 （t ），…，sq （t ） ]T，A（t ） 为M × q 阶阵列A（θ ） = [ a （θ1 ），…，a（ θq ） ]T. 此时接收信号r （t ）的四阶累积量为

cum（ ri，rj，rk，rl ）= E { ri，rj，rk，r }l - E { ri rj } E { rk rl }-E { ri rk } E { rj rl }- E { ri rl } E { rj rk }

其中1 ≤ i，j，k，l ≤ M.

很多文献对高阶累积量的计算也有研究，本文针对色噪声条件下的信号处理问题，通过利用高阶累积量矩阵来代替协方差矩阵，对阵列信号进行运算，其形式为

2 传感器节点检测状态控制

在线性传感器阵列中，传感器节点沿直线方向布放. 当目标出现时，信号强度随节点到目标间距离的增加而减小，距离很远处的节点接收到信号中目标成分很弱；在近距离范围内，由于障碍物遮挡等因素，也会导致部分节点接收不到明显目标信号.考虑到这类节点的数据对最终目标检测贡献不大，此时应对参与阵列协同检测的节点个数进行控制，提高协同检测的效率.

地震波传感器采集的是信号的三轴震动信号，具有矢量输出的特性. 当目标存在时，其多通道之间采集的信号具有明显的相关特性；当目标不存在时，其采集的为噪声信号，此时各通道之间的噪声不相关. 利用这一特点，在传感器节点端构建矢量信号的协方差矩阵，求解矩阵的特征值，利用信号相关性不同的条件下协方差阵的特征值特点构建节点状态控制量，结合设定的数据发送门限值对节点的检测状态进行控制.

首先构建节点状态控制量Γ. 设定目标信号为s （m），m = 1，2…，M 为节点采集的信号点数，噪声信号为n （m），服从N （0，σ2m ）的高斯分布. 此时，节点的状态控制可表示为二元假设检验问题：

地震波传感器接收到三轴加速度信号时，首先求取信号的协方差矩阵，进行特征值分解，获得信号的最大特征值λmax 和最小特征值λmin. 接收的信号包含目标和不包含目标时其协方差矩阵的最大特征值与最小特征值之比不同，利用此特点构建Γ.

对三通道的地震波传感器，由于其相互垂直的特性，各通道之间接收的噪声信号一般不相关；当存在随机入侵的目标时，目标信号在各通道之间的具有相关性. 假设传感器三个通道对信号采样，每个通道采样点数为M，则采集信号可表示为：

其中ax （k）、a y （k）、az （k） 分别为传感器x、y、z 轴在第k次采样的输出.

传感器三轴之间接收的噪声与目标信号之间是不相关的，此时采集信号的协方差矩阵可表示为RA = RS + σ2nI，其中I 为单位矩阵，S （k）、N （k） 分别是目标信号向量、噪声向量，其表达式为：

在H0 条件下，协方差阵只包含噪声信号，此时分解的最大特征值λmax 和最小特征值λmin 均为噪声信息；在H1 条件下，协方差阵中包含了目标信号和噪声信号，此时分解的最大特征值λmax 为目标信号信息，最小特征值λmin 为噪声信息. 利用协方差阵的最大最小特征值之比可以构建与目标是否存在有关的节点状态控制量Γ：

Γ = λmax／λmin

如需对节点状态进行控制，还需要设定传感器节点的数据发送触发门限q. 门限值利用数据进行计算时，通过求取无目标时多个传感器节点测量结果特征值之比的均值，可以得到较优的门限值，但在实际中很难预先获得多个节点的特征值，且计算复杂度高. 因此，可以通过对数据抽样利用经验分布计算触发门限q 的经验值. 首先，对采集的数据进行抽样，利用抽样数据来估计目标协方差矩阵：

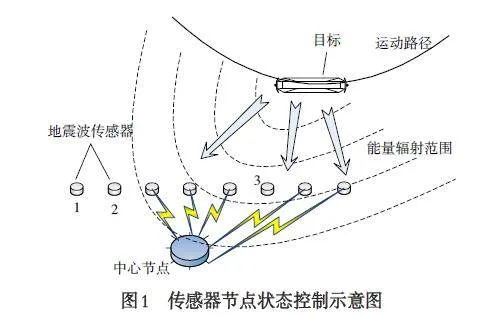
式中的Δ为控制参数，其值的设定根据节点控制的松紧程度以及环境噪声强度决定，取值范围为（0，1）. 在t 时刻，地震波传感器节点获取目标监测值并计算状态控制量Γt，当Γt ≥ q 时，则传感器节点识别为存在目标，向中心节点发送采集数据并进入下一个监测周期Δt；若传感器节点在t + Δt 时刻获得的状态控制量Γt + Δt 仍然满足Γt + Δt ≥ q，则识别为目标仍然在监测范围内，继续发送采集数据；持续重复此过程，直到传感器节点获得的状态控制量Γt + NΔt满足Γt + NΔt lt; q，这时节点判断为监测区域内不存在目标，停止数据发送. 传感器节点的检测状态控制如图1 所示.

从图1 中可以看到，目标的能量只在一定的辐射范围内具有有效强度，当地震波传感器节点距离目标较远时将不能接收到目标信号，如节点1、节点2；同时在目标有效辐射范围内，由于海底不平坦或遮挡物的影响也会导致传感器接收不到目标信号，如节点3. 此时，通过节点状态控制，可以有效控制参与全局检测的传感器节点个数，减少无效数据的传输与干扰.

3 高阶累积量相关性目标检测算法

地震波传感器阵列中心节点在一个检测周期内收到传感器节点发送的数据后，对多路数据进行全局处理，求解传感器阵列的四阶累积量矩阵，通过求解累积量矩阵的相关性，构建检测统计量. 当目标存在时，参与检测的传感器节点采集信号来源于同一个信号源，此时信号之间应具有明显的相关性；当目标不存在时，通过检测状态控制只有少量传感器节点将数据发送到中心节点参与目标检测，此时传感器节点采集的主要为噪声信号，信号之间不具有明显的相关性. 在此方法中，首先假设累积量矩阵C和相关性参数σ 为已知的，据此在广义似然比检测（GLRT）准则下求解目标x 的极大似然估计x̂，并利用这些参数构建目标检测器；得到x̂后再利用采集数据估计累积量矩阵C 和相关性参数σ，来对目标进行检测.

3.1 传感器阵列数据量测模型

本文使用的地震波传感器具有矢量特性，其三个轴向的输出之间具有相关性，假设传感器输出为ax、a y、az，则构建传感器输出矢量：

H0 假设为不存在目标，H1 假设为存在目标，通过对假设的检验来给出目标是否存在的最终判决.

3.2 基于相关性的判决统计量

首先假设累积量矩阵C 和相关性参数σ已知，根据GLRT 判决准则估计目标x，求解x 的最大似然估计（MLE）值x̂；获得x̂后，利用多通道采集的数据来估计C 和σ 的MLE 值Ĉ和σ̂；最后，利用获得的参数估计值来构造判决统计量Λ[9]. 利用以上构造的量测模型，则目标检测的二元假设问题可用概率密度函数表述为：

式中： |C |为矩阵C的行列式，etr （·）为矩阵（·）迹的幂，AH 为A 的Hermite 矩阵，且V0 = AAH、V1 =（ A -Bx ）（ A - Bx ）H.

利用前述假设，则目标检测的判决统计量可表示为：

5 检测方法性能仿真

通过仿真实验验证目标检测方法的检测性能.实验中假设目标服从零均值的高斯分布，传感器节点个数为M，地震波传感器由三个通道进行数据采集，即N = 3，对单个目标进行检测. 在对水下水中目标进行检测时，信号信噪比SNR 的定义为：

5.1 基于相关性检测方法性能仿真

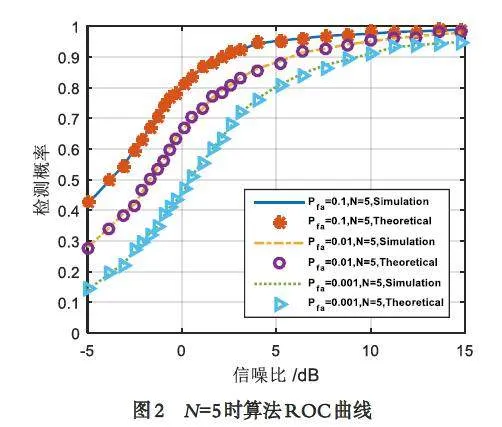
将检测算法的理论检测值与仿真结果进行比较. 理论计算值由检测概率计算公式计算得到，其中虚警概率为恒定值，先计算得到检测门限，带入方程计算检测概率值. 仿真实验采用蒙特卡洛数值仿真方法，将多次仿真结果取均值得到仿真结果. 仿真环境设定为：节点控制参数设定为0.5，相关性参数设定为0.8，信噪比变化范围为-5 ～ 15 dB，经1 000 次仿真实验，分别研究在传感器节点数N 为5和10，虚警率Pfa 为0.1、0.01 和0.001 时算法的检测性能. 首先，研究在恒虚警条件下，节点数为5 时目标检测概率随信噪比变化情况，结果如图2 所示.

图2 中横轴为信噪比SNR，纵轴为检测概率，散点表示检测算法在不同虚警率下的理论检测值，连接线表示检测算法1 000 次仿真计算结果的均值.可以看到，在不同信噪比和虚警率条件下，理论检测值与仿真结果均有很高的吻合度，显示了理论计算的正确性. 在其它参数相同时，固定信噪比下算法检测概率随虚警率的增加而增加.

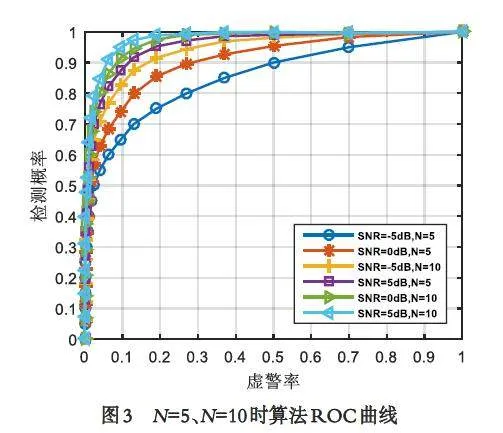
分别固定信噪比SNR 为-5 dB、0 dB、5 dB，节点个数N 为5、10，其他仿真条件与以上相同，得到算法ROC 曲线如图3 所示.

图3 显示了检测概率随虚警率变化的情况. 可以看到，在相同条件下，随着算法虚警率的增加，检测概率也得到提高：在虚警率小于0.1 时，随着虚警率的增加检测概率迅速提升；在虚警率大于0.1 后，检测概率的增加速度变缓；当虚警率大于0.5 后，检测概率变化缓慢，趋于平稳. 在节点数为5 和10 时，检测概率均随信噪比的增加而得到提升，在N = 5时提升的幅度大于N = 10，这是由于节点数增加后检测性能趋近于算法理论性能. 在SNR 为-5 dB、0dB、5 dB 时，检测概率均随节点数的增加而提高. 对比两种因素影响下的检测概率提升幅度可以发现，节点数对算法检测性能的影响更加显著，提升效果更明显. 由此可以看到，算法在较低信噪比下仍可有效检测出目标，且检测性能对节点数依赖明显，较少的节点数会明显降低目标检测性能.

5.2 不同检测方法性能比较

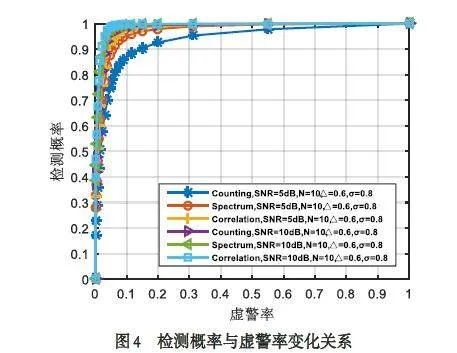
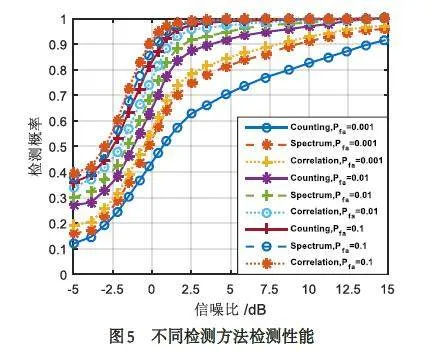
通过对比集中不同目标检测方法在相同条件下的检测性能，来验证相关性目标检测方法的优越性能. 首先，研究不同算法在固定信噪比条件下的检测性能. 仿真参数设置为：节点个数N = 10，节点控制参数设定为Δ = 0.6，相关性参数设定为σ = 0.8，固定信噪比分别为5 dB、10 dB，经1 000 次仿真实验，得到检测概率与虚警率变化关系如图4 所示.

从图4 可以看出，在SNR 为5 dB 和10 dB 条件下，Correlation 算法（本文算法）均表现出更好的检测性能. 这是由于基于相关性的检测方法一方面控制了参与阵列检测的节点数量，事实上提高了接收信号的信噪比，也就提高了采集信号的利用效率；另一方面充分利用了不同节点对同一目标检测时获取数据的相关特性，通过构建相关性检测量来对目标进行可靠检测. 对比也可以发现，在信噪比较低时Correlation 算法的这种优势更加明显. 为分析在不同信噪比下Correlation 算法的检测性能，通过固定虚警率来考察不同算法的检测性能. 在恒虚警条件下不同检测方法检测性能随信噪比变化情况如图5所示.

6 结语

本文以实现地震波传感器阵列目标可靠检测为目的，研究了阵列信号高阶累积量相关性目标检测方法. 针对远场噪声环境下传统决策级判决检测方法虚警率高、信息浪费问题，提出基于高阶累积量矩阵相关性目标检测方法，可有效消除噪声对检测结果影响. 对提出的算法性能进行仿真，仿真结果显示了相关性目标检测方法的有效性和优越性.

参考文献：

[1] 罗俊海，杨阳. 基于数据融合的目标检测方法综述[J]. 控制与决策，2020，35（1）：1-15.

[2] 闫永胜，王海燕，董海涛，等. 基于传感器网络的在线决策融合目标检测方法[J]. 系统工程与电子技术，2015，37（8）：1741-1747.

[3] LIU T， ZHANG Z， LEI Z. An approach to ship target detec⁃tion based on combined optimization model of dehazing anddetection[J]. Engineering Applications of Artificial Intelli⁃gence. 2024， 127（B）： 107332. doi： 10.1016/j. engappai.2023.107332.

[4] 安浩南，赵明，潘胜达，等. 基于伪模态转换的红外目标融合检测算法[J]. 光子学报，2020，49（8）：176-188.

[5] 许琦敏，万峻，何羚，等. 基于高阶累积量和信号平方谱特征的复合调制信号盲识别[J]. 电子学报，2022，50（2）：426-431.

[6] 高永婵，潘丽燕，李亚超，等. 空/时对称阵列雷达非高斯杂波背景下多秩距离扩展目标检测方法[J]. 雷达学报，2022，11（5）：765-777.

[7] STOICA P， NEHORAI A. MUSIC， maximum likelihood，and Cramer-Rao bound[J]. IEEE Transactions on Acoustics，Speech， and Signal Processing， 1989， 37（5）： 720-741. doi：10.1109/29.17564.

[8] STOICA P， NEHORAI A. MUSIC， maximum likelihood，and Cramer-Rao bound： further results and comparisons[J].IEEE Trans on ASSP， 1990， 38（12）： 2140-2150. doi：10.1109/29.61541.

[9] PARK H R， LI J， WANG H. Polarization-space-time do⁃main generalized likelihood ratio detection of radar targets[J].Signal Processing， 1995， 41（2）： 153-164. doi：10.1016/0165-1684（94）00097-J.

[10] McDONOUGH R N， WHALEN A D. Detection of Signalsin Noise[M]. New York， USA： Academic Press， 1995：151-200.

[11] ANDERSON T W. An Introduction to Multivariate Statisti⁃cal Analysis[M]. New York， USA： John Wiley amp; Sons， 2003.

[12] KELLY E J. Finite-sum expressions for signal detection prob⁃abilities[EB/OL]. [2023-01-30]. https：//www. mendeley.com/catalogue/4119e590-fb2a-37e7-a329-ce8a05e8afec.

【编校：王露】

基金项目：国防预研资助基金项目（51401020503）