Janus ZrBrI 光电性质的第一性原理计算

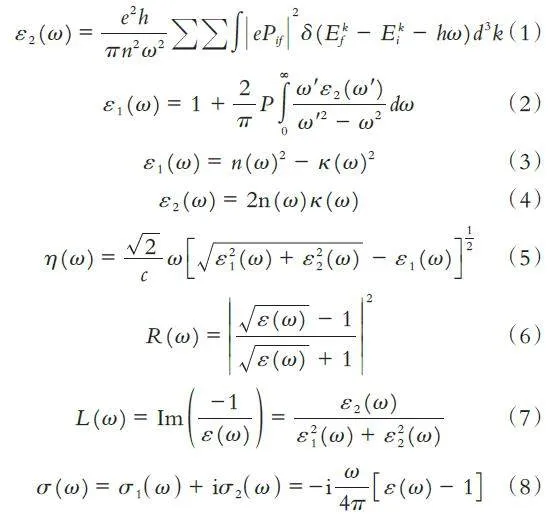
摘 要：基于密度泛函理论，采用第一性原理的平面波赝势法系统计算ZrI2和Janus ZrBrI 的几何结构、电子性质和光学性质.几何结构分析发现Janus 结构对键长及单层厚度都存在一定影响. 基于HSE06 泛函计算结果表明ZrI2和Janus ZrBrI 均为准直接带隙半导体，禁带宽度分别为0.84、1.01 eV，其价带和导带主要由Zr 的4d 态电子构成. 同时，Janus 结构能形成内建电场，进一步抑制电子空穴对的复合. 利用介电函数计算得到折射率、反射谱、吸收谱、光电导率和能量损失函数等光学参数，光学性质分析表明ZrI2和Janus ZrBrI 在可见光的吸收系数可达10-4 cm-1，Janus 结构能够实现吸收峰的蓝移.

关键词：Janus ZrBrI；第一性原理；电子结构；光学性质

中图分类号：O469

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.13

自2004 年成功剥离出石墨烯以来，二维材料成为科学家们研究的热点[1-4]. 其中，二维半导体材料由于具有原子级厚度及独特的能带结构，在光电器件应用领域展现出独特的优势[5]，得到科学界的关注，被广泛应用于微电子器件领域，尤其可以作为光电探测器的基础材料. 同时，二维半导体材料在太阳能光催化领域也可作为析氢反应和碳捕获的催化剂[6]. 王根旺等概述了几种常见的二维半导体材料，分析了材料的结构、性质及其在纳米器件中的应用[7]. 2018 年王新江等对Bi/Sb 基硫卤化物、氧卤化物和二维过渡金属硫化物（TMDCs）的超晶格结构展开高通量计算，理论上设计并筛选出了三类具有较高光电转换效率的Bi/Si 基卤化物作为优异的光电材料候选者[8]. 这种通过理论设计出半导体光电材料来丰富半导体光电材料家族种类的方法，是一种光电材料学领域的新发展思路，有巨大的应用价值. 但许多二维半导体材料却由于其存在的缺点，如：石墨烯的零带隙特性[9]、MoS2 的低载流子迁移率[10]等，在实际应用中有局限性. 幸运的是，科学家们寻找到了一批化学剂量简单、化学稳定性强、实验可行性好、集光能力强的新型二维半导体材料，如二维ZrI2[11].

ZrI2、ZrBr2这类物质属于过渡金属二卤化物，研究人员对这类物质进行了研究. 2021 年Huang 等人利用第一性原理计算，理论上证明了单层二卤化锆材料ZrX2 （X = Cl，Br 和I）体现出优异的光电性能，在光电材料领域有潜在的应用价值[11]；单层ZrX2能通过简单的机械剥离从体相获得，且具有良好的动力学、热力学和力学稳定性，具备实验合成可行性.在实验上，Corbett 等人在1982 年合成了一种弱范德华力叠加的层状化合物β-ZrI2[12]，推动了二维锆基卤化物的研究热潮. Jiang 也在2011 年对四种简单的TMDC 材料MX2 （M=Zr 和Hf，X=S 和Se）进行结构和电子性质的研究[13]. ZrI2这种过渡金属二卤化物，以其准二维层状结构为特征，具有丰富的化学和物理性质. 但以第一性原理为研究手段，对ZrI2的结构和电子性质的研究仍缺乏全面的认识[14]，在其Janus结构的研究上，也暂未见报道. Janus 材料由于它的双面不对称特征，有着极大的研究价值，尤其在光学和电子领域具有一定的应用前景，许多科学家对其进行了广泛的研究[15-17]. 如2019 年，Zhang 等人用第一性原理计算方法研究了方形相MX2和Janus MXY（M = Mo，W；X，Y = S，Se，Te）过渡金属二卤族化合物单分子膜，证明Janus 1S-MXY 系统本质上具有自旋劈裂，其中1S-WSTe 单层在3% 的压缩应变下的自旋劈裂最大[18]. 2021 年Chaney 等人也利用第一性原理和机器学习方法综合研究锂在Janus Mo/WXY（X，Y = S，Se，Te）上的吸附和扩散，探索二维Janus 过渡金属二卤族化合物（TMDs）在锂离子电池电极上的应用[19].

本文通过打破ZrI2的镜面对称结构将一层碘原子替换为与其性质相似的溴原子，构建Janus ZrBrI，并通过第一性原理计算Janus ZrBrI 的电子结构（能带结构、电子态密度）和光学性质（介电函数、复折射率、光电导率、能量损失函数、吸收谱和反射谱），旨在拓展锆基卤化物的设计思路，为锆基卤化物在光电材料领域的应用提供理论依据.。

1 计算模型及计算方法

基于投影缀加波（PAW）方法，利用密度泛函理论（DFT）为基础的维也纳从头计算模拟包（VASP，Vienna Abinitio Simulation Package）实现几何优化、电子结构和光学性质的计算[20-22]，采用广义梯度近似（GGA）和PAW 进行几何优化[22-23]. 为了描述电子交换和关联能，使用Perdew-Burke-Ernzernof（PBE）和Heyd-Scuseria-Emzerhof（HSE06）[24]泛函，由于PBE 计算能带存在带隙低估问题，所以使用HSE06 来获得更加精确的电子结构并与PBE 计算结果比较. 在第一布里渊区以Γ为中心的对称点，其网格采样密度为0.02 × 2π/Å. 整个计算过程中，平面波截止能设置为500 eV，自洽过程能量和应力收敛阈值设置为10-6eV 和0.01 eV/Å. 垂直于表面，添加了15 Å 的真空，以避免相邻两层图像间的耦合效应. 由于Janus ZrBrI 具有非对称结构，计算过程中添加了偶极矫正[25].

2 计算结果与讨论

2.1 几何模型与平面平均静电势

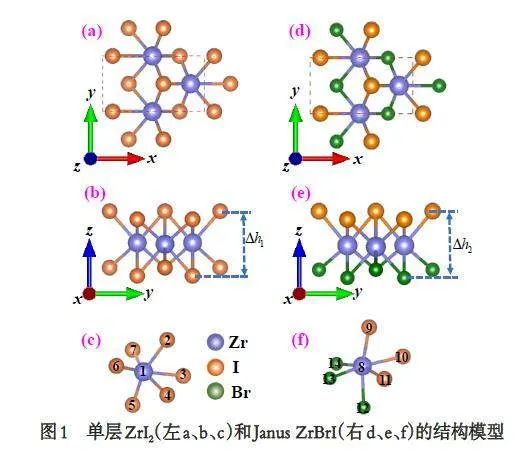
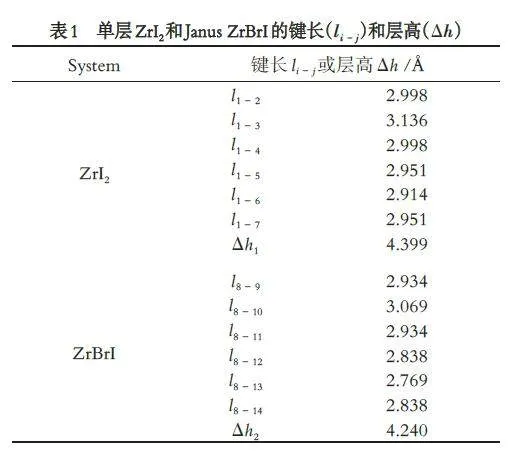
单层ZrI2的结构模型如图1 所示. 单层ZrI2结构从具有Pmn21 （No.31）空间群的体相β-ZrI2获得[11]，图1a、图1b 表明一个晶胞由2 个Zr 原子4 个I 原子构成. 在ZrI2结构基元中，一个Zr 原子与6 个I 原子相连，具有典型的1T’-MX2 结构[11]. 在ZrI2 单分子层中，用Br 原子替换I 原子的两个原子层中的一个子层形成了Zr 原子夹在I 原子与Br 原子层间的三明治Janus ZrBrI 结构（图1d、图1e）.Janus ZrBrI 在空间群晶格保持不变的情况下，一个晶胞由2 个Zr 原子、2个I 原子、2 个Br 原子组成，一个Zr 原子与3 个I 原子、3 个Br 原子成键，键角和键长发生变化（图1c、图1f，表1）.单层ZrI2 中Zr-I 键长为2.914 ～ 3.136 Å，表现出ZrI6八面体的Jahn-Teller 变形. 1-2 键与1-4键键长相等，1-5 键和1-7 键键长相等. Janus ZrBrI键长为2.769 ～ 3.069 Å，具有类似于ZrI2畸变结构的Jahn-Teller 变形. Janus ZrBrI 键长等量关系不变：8-9 键与8-11 键键长相等，8-12 键与8-14 键键长相等. Janus ZrBrI 结构相对ZrI2 的所有键键长一一对应变短，尤其是替换为Zr-Br 键的部分，这与I 原子与Br 原子电负性差异有关. 对比I 原子，Br 原子电负性更大，Zr-Br 键比原来的Zr-I 键键长更短，单层层高Δh 由4.399 Å 减小为4.240 Å，二维材料厚度变薄.

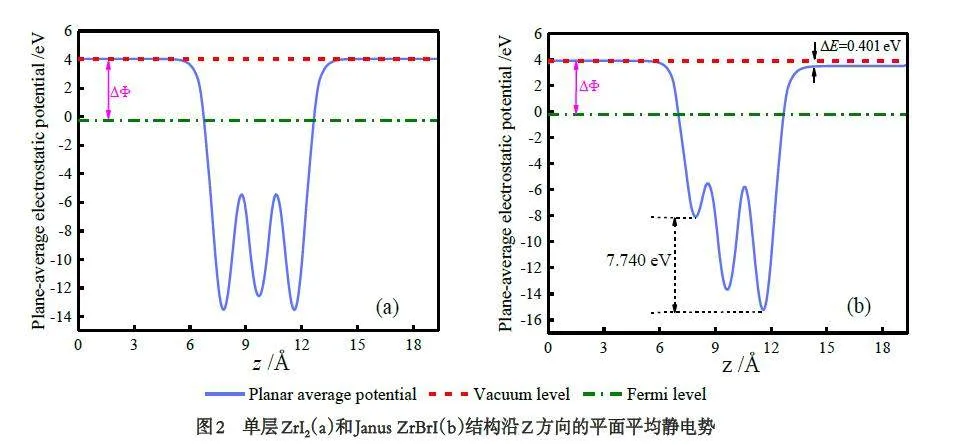
图2a、图2b 表示两种结构沿z 方向的平面平均静电势. 图2a 中真空能级为4.050 eV，费米能级为-0.265 eV，功函数ΔΦ为4.315 eV. 图2a 左右平台高度一致，平面平均静电势曲线轮廓完全对称，左右两侧不存在静电势差，主要是由于两侧都是I 原子，电负性相同. 图2b 中真空能级为3.901 eV，费米能级为-0.257 eV，功函数ΔΦ为4.158 eV. 图2b 左右平台高度不一致，高度差值ΔE 为0.401 eV，平面平均静电势曲线轮廓不对称，存在静电势差. Br-Zr 原子侧静电势低于I-Zr 原子处，电势差为7.740 eV，因为Br 比I 电负性更强[26]，更多电子被转移至Br 原子，Br原子收集电子形成负电中心，I 原子则形成正电中心，内部产生极化，形成内建电场. 内建电场的存在可以在不需要额外的外部电源提供能量的情况下，实现材料内部光电子能量的转换，这为自供电光电材料的应用提供了可实现的基础.

2.2 电子结构

为了研究Br 原子替换I 原子形成Janus 结构的电子特征，对ZrI2 和Janus ZrBrI 的能带结构（BS）和态密度（DOS）进行了计算. 如图3a 所示，本征单层显示出准直接带隙特征. 由PBE 计算得到本征单层ZrI2的价带最大值（VBM）为-0.210 eV，导带最小值（CBM）为0.217 eV，带隙值为0.427 eV；由HSE06 计算出本征单层ZrI2 VBM 为-0.423 eV，CBM 为0.416 eV，带隙值为0.839 eV. 对于Janus ZrBrI，同样表现出准直接带隙特征，由PBE 计算得到VBM 为-0.208 eV，CBM 为0.285 eV，带隙值为0.493 eV；由HSE06 计算得到VBM 为-0.327 eV，CBM 为0.681eV，带隙值为1.008 eV. 由此可以看出，Br 原子替换I原子形成Janus 结构有增加带隙值的效应. 从DOS（图3c、图3d）可以看出，Br 原子替换I 原子形成Janus结构对价带和导带的轨道贡献没有明显影响，Janus结构形成前后深层次的态密度主要是由I-p 轨道所形成，费米能级附近的态密度主要是由Zr-d 和I-p杂化轨道所形成.

2.3 光学性质

光学性质可以通过复介电常数描述固体宏观光学响应函数. 对于复介电常数ε（ ω） = ε1 （ ω） +iε2 （ ω）（ε1 （ ω） 和ε2 （ ω） 分别是复介电常数的实部和虚部[27-28]），通常首先得到材料的复介电常数的虚部，借助相关的转化关系式推知复介电常数的实部以及物质其余的光学性质（吸收系数、反射系数、能量损失函数、光电导率、消光系数等）[29]，相关公式如下：

式中：e 为电场的极化方向，Ef 为最终态的结合能，Ei为初始结合能，k 为布里渊区内高对称性的一些特殊点，ω 为角频率（2πν），ω′为角频率（2πν′），Pif 为动量跃迁矩阵元，n （ ω） 为折射率，κ （ ω） 为消光系数，η（ ω）为吸收系数，R （ ω）为反射系数，L （ ω）为能量损失函数，σ （ ω）为光电导率.

2.3.1 复介电常数

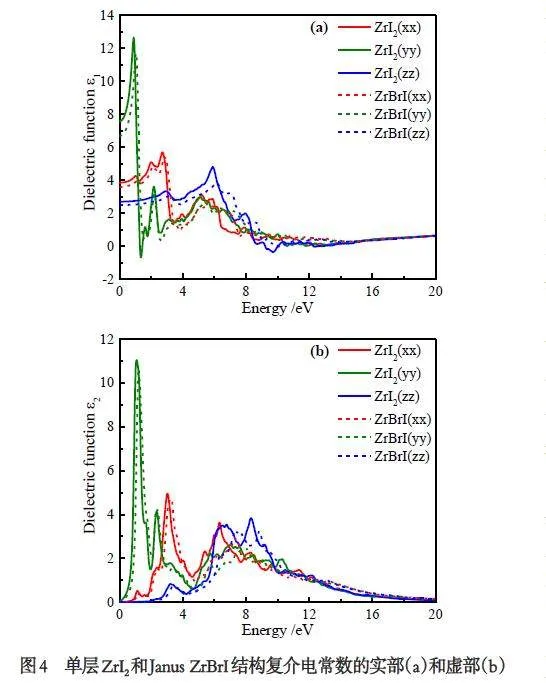
复介电常数虚部可由公式（1）计算出后，再由公式（2）推知复介电常数实部，进而得到复介电常数实部和虚部的图像（如图4）.图4 是复介电常数实部和虚部沿x、y、z 方向的函数图像，xx、yy、zz 表示光偏振沿x、y、z 方向的情况，光偏振沿三个方向具有各向异性[30]，表现为复介电常数在不同的方向上表现出不同的数值且具有较大的差异，但是随着光子能量的增大，差异变得越来越小，x、y、z 方向的值最终相等并趋于一个稳定值. 从整体趋势来看，ZrI2和Ja⁃nus ZrBrI 介电常数实部的值随着光子能量的增大而下降. ZrI2 在x、y、z 方向上的ε1 峰值分别为5.701、12.653、4.809，对应光子能量为2.711、0.894、5.899eV，y 方向的ε1 峰值远远大于x、z 方向的峰值. 图4b可以看出随着光子能量的增加，ZrI2和Janus ZrBrI 介电常数虚部的值整体呈下降趋势. ZrI2介电常数虚部在x、y、z 方向上的最大峰值分别为4.950、11.045、3.844，对于光子能量分别为3.009 eV、1.073 eV、8.313 eV，Janus ZrBrI 的最大峰值大小与分布情况与ZrI2基本相同. 整体上看，构建Janus ZrBrI 使复介电常数的实部和虚部都发生了一定程度的蓝移，说明Janus ZrBrI 对于高能量光谱具有较高的敏感性.

2.3.2 光学性质

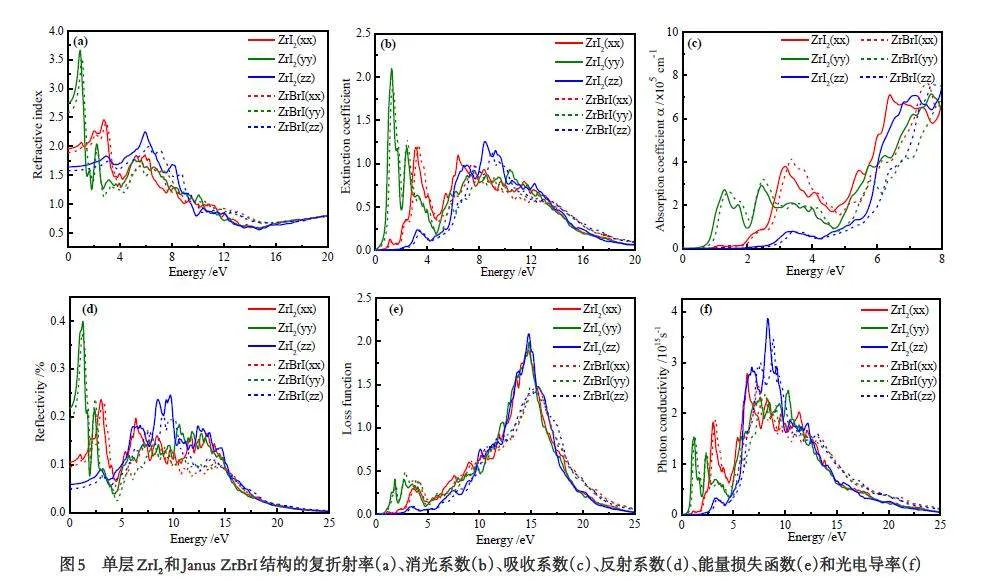
固体宏观光学响应函数通常可以由复折射率来描述，同样可以利用公式（3）（4）由介电函数的实部与虚部推导出，得到的复折射率图像如图5a 所示.ZrI2沿x、y、z 方向的静态折射率分别为1.968、2.758、1.637，构建Janus ZrBrI 结构后，静态折射率略微变小. ZrI2 和Janus ZrBrI 的折射率峰值主要分布在0.912 ～ 6.995 eV 范围内，最大的峰值为y 方向在～0.9 eV 光子能量处，大小为～3.7. 相对ZrI2，Janus Zr⁃BrI 折射率图像蓝移.

图5b 是ZrI2 和Janus ZrBrI 的消光系数图像.ZrI2和Janus ZrBrI 消光系数的主要峰值出现在光子能量为1.076 ～ 3.406 eV 和6.389 ～ 11.591 eV 范围内，在11.591 eV 以后，ZrI2和Janus ZrBrI 消光系数逐渐降低并趋近于0. 同时，ZrI2 和Janus ZrBrI 消光系数与相对介电函数虚部成正比. Janus ZrBrI 对比ZrI2，在1.076 ～ 3.406 eV 光子能量范围内，消光系数图像蓝移.

物质的光吸收系数指光在物体中进行传播时材料对光的吸收能力[31]. 借助复介电常数可由公式（5）推导出ZrI2 和Janus ZrBrI 的光吸收系数如图5c 所示. 图5c 表示光偏振沿x、y、z 方向时物质的吸收系数在一定光子能量范围内的分布情况. 由图5c 可知，ZrI2和Janus ZrBrI 光吸收能力覆盖大部太阳光谱（从红外光到紫外光），实现宽谱线范围内吸收太阳光. 在可见光（1.63 ～ 3.18 eV）区域[25]，ZrI2 和JanusZrBrI 在x 和y 方向上表现出明显的吸收峰，最高峰值达3.723×105 cm-1，是ZrI2 在光子能量为3.158 eV处x 方向上的吸收系数. 已知在太阳辐射能中，可见光占据太阳总辐射的50%[32]，上述分析表明该材料具有对太阳光的高效率吸收性能. 在紫外光区域（光子能量大于3.18 eV），ZrI2 和Janus ZrBrI 在三个方向上的吸收系数先是随着光子能量的升高而降低，在4.626 eV 光子能量附近抵达波谷后陡然上升分别到达最高峰，最大峰值为7.643×105 cm-1，是Ja⁃nus ZrBrI 在光子能量为7.558 eV 处x 方向上的吸收系数. ZrI2 和Janus ZrBrI 的三个方向在紫外光区域具有高吸收峰，表明物质对紫外光的响应很强，可应用于紫外吸收剂，以及与之相关的光电器件[26]. 对比本征ZrI2，在构建Janus ZrBrI 结构后，Janus ZrBrI 在可见光及红外光区域光吸收系数略微增大，且图像蓝移，说明物质的光吸收能力变强，可作为太阳能电池，光催化领域的候选材料[31]. 蓝移现象的原因可能是Janus ZrBrI 层高减小，量子尺寸效应增强导致能隙变宽，从而导致光吸收带移向短波方向.

反射系数指的是物体反射的能量占总能量的百分比. 反射系数可借助复介电常数而由公式（6）推导出. 由图5d 可以看出ZrI2和Janus ZrBrI 整体反射系数值偏低，最大值不超过0.4，较低的反射系数意味着较少的入射光被反射，该现象为它们成为良好的吸收层材料提供了有利条件[33]. ZrI2和Janus ZrBrI反射主要发生在光子能量为0.866 ～ 3.369 eV 的低能区. 在光子能量为3.369 ～ 4.668 eV 的紫外光区域，ZrI2和Janus ZrBrI 的反射系数在4.087 eV 附近达到最小值为0.024. 在光子能量大于15 eV 后，ZrI2和Janus ZrBrI 反射系数值逐渐降低为0，这对光吸收和折射特性的研究有利[34]. 构建Janus ZrBrI 结构后，可见光区域和红外光区域反射图像有蓝移现象产生，在光子能量4.668 ～ 14.905 eV 的高能区，反射系数降低，材料对于光的利用率提高.

能量损失函数是描述电子通过均匀电介质时，表征电子损失的物理量，其数值代表等离子体的震荡关联特征[29]. 从介电函数可以得到电子的能量损失函数，它描述了电子通过均匀的介电质时能量的损失情况. 由图5e 可知在能量达到～15 eV 时能量损失最大，光子能量达到25eV 时趋于零. 构建JanusZrBrI 结构后，能量损失图像发生蓝移现象，在高能区的能量损失降低，ZrI2三个方向的能量损失约为2.0，而ZrBrI 在15.4 eV 时三个方向均达到顶峰，能量损失约为1.4.

光电导是指在固体吸收光子后，其自由载流子数目增加而出现的电导率的增量. 光子能量必须大于半导体的禁带宽度才能产生光电导效应. 光电导效应在光电导型辐射探测器件中是很重要的指标，光电导效应也是是半导体各种光电子应用的物理基础. 图5f 可以看出ZrI2的光电导率主要峰值出现在6.7 ～ 12.2 eV 的能量范围内，构建Janus ZrBrI 结构后，光电导率图像发生蓝移现象.

3 结语

基于密度泛函理论，采用第一性原理的平面波赝势法系统地实现了对ZrI2和Janus ZrBrI 的几何优化、电子结构和光学性质的计算. 计算结果表明：Ja⁃nus ZrBrI 对比ZrI2，单层层高变小，键长变短. JanusZrBrI 和ZrI2均为准直接带隙半导体，价带和导带主要由Zr-4d 态构成. 用Br 原子替换I 原子形成Janus结构有增加带隙值的效应. 不仅如此，Janus 结构还能形成内建电场，进一步抑制电子空穴对的复合.光学性质的分析表明，ZrI2和JanusZrBrI 的介电常数虚部显示出较多的峰值，具备优异的光吸收能力.在可见光区域，ZrI2和Janus ZrBrI 的折射率和吸收系数具有较为明显的峰值，低能区吸收系数峰值最高达3.723×105 cm-1. 在紫外光区域，ZrI2和Janus ZrBrI均具有高吸收峰，表明物质对紫外光存在较强的光响应. ZrI2和Janus ZrBrI 整体反射系数值偏低，最大值不超过0.4. 对比本征ZrI2，构建Janus ZrBrI 结构后，物质的Janus 结构可以实现了复介电函数、复折射率、吸收谱、反射谱、光电导率和能量损失函数峰值的蓝移，可实现对本征ZrI2光学性质的微调.

参考文献：

[1] 杨卫. 应变工程与表面钝化调控二维材料性能的第一性原理研究[D]. 合肥： 中国科学技术大学， 2022.

[2] 袁苗嘉. 新型二维材料电子结构及磁学性质的研究[D]. 济南： 山东建筑大学， 2022.

[3] 蔡超群. 二维材料增强微纳光纤环谐振器光场调控技术研究[D]. 南京： 南京邮电大学， 2022.

[4] 王长天. 几种二维材料结构及其物性的第一性原理计算研究[D]. 北京： 中国科学院大学（中国科学院物理研究所），2022.

[5] 黄彦民， 袁明鉴， 李玉良. 二维半导体材料与器件——从传统二维光电材料到石墨炔[J]. 无机化学学报， 2017， 33（11）：1914-1936.

[6] 刘昱良. 二维材料电子结构调控及光解水产氢的理论研究[D]. 长春： 吉林大学， 2022.

[7] 王根旺， 侯超剑， 龙昊天， 等. 二维半导体材料纳米电子器件和光电器件[J]. 物理化学学报， 2019， 35（12）： 1319-1340.

[8] 王新江. 新型半导体光电材料的理论筛选与优化设计[D].长春： 吉林大学， 2018.

[9] SUZUKI H， OGURA N， KANEKO T， et al. Highly Stable Persistent Photoconductivity with Suspended Graphene Na⁃noribbons[J]. Scientific Reports， 2018， 8（1）： 11819. doi：10.1038/s41598-018-30278-z.

[10] CHEN C， WANG M， WU J， et al. Electronic structures and unusually robust bandgap in an ultrahigh-mobility layered ox⁃ide semiconductor， Bi2O2Se[J]. Science Advances， 2018， 4（9）：eaat8355. doi： 10.1126/sciadv.aat8355.

[11] HUANG X， ZHUO Z， YAN L， et al. Single-layer zirco⁃nium dihalides ZrX2 （X = Cl， Br， and I） with abnormal ferro⁃elastic behavior and strong anisotropic light absorption ability[J]. Journal of Physical Chemistry Letters， 2021， 12（32）： 7726-

7732. doi： 10.1021/acs.jpclett.1c01958.[12] CORBETT J D， GUTHRIE D H. A second infinite-chain form of zirconium diiodide （β） and its coherent intergrowth with α-zirconium diiodide[J]. Inorganic Chemistry， 1982， 21（5）： 1747-1751. doi： 10.1021/ic00135a009.

[13] JIANG H. Structural and electronic properties of ZrX2 and HfX2（X = S and Se） from first principles calculations[J]. Journal of Chemical Physics， 2011， 134（20）： 204705. doi： 10.1063/1.3594205.

[14] 岳子豪， 张会. 新型SiAsP 二维Janus 材料电子结构和光吸收性质的第一性原理研究[J]. 功能材料，2022， 53（9）： 9141-9146.

[15] 范英才， 马西奎， 王君茹， 等. 二维Ⅲ族硫化物Janus 多层结构的高效光解水特性：内建电场和空位缺陷效应（英文）[J].科学通报， 2020， 65（1）： 27-34.

[16] 王盼， 宗易昕， 文宏玉， 等. 二维Janus 原子晶体的电子性质[J]. 物理学报， 2021， 70（2）： 110-126.

[17] HE Q W， WU Y， YANG C H， et al. Switch effect on con⁃trolled water splitting by biaxial strain regulating the promis⁃ing two-dimensional Janus X2PAs （X= Si， Ge and Sn） photo⁃catalyst[J]. Nanoscale， 2023， 15（24）： 10458-10464.. doi：10.1039/d3nr01760e.

[18] ZHANG Y， YE H， YU Z ， et al. First-principles study of square phase MX2 and Janus MXY（ M =Mo， W; X ， Y =S，Se， Te） transition metal dichalcogenide monolayers under bi⁃axial strain[J]. Physica E： Low-dimensional Systems and Nanostructures， 2019（110）： 134-139. doi： 10.1016/j. physe.2019.02.009.

[19] CHANEY G， IBRAHIM A， ERSAN F， et al. Comprehen⁃sive study of lithium adsorption and diffusion on Janus Mo/WXY （X， Y = S， Se， Te） using first-principles and machine learning approaches[J]. ACS Applied Materials amp; Interfaces，2021， 13（30）： 36388-36406. doi： 10.1021/acsami.1c05508.

[20] KRESSE G， FURTHMÜLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave ba⁃sis set[J]. Physical Review B， Condensed Matter， 1996， 54（16）： 11169−11186. doi： 10.1103/physrevb.54.11169.

[21] KRESSE G. Ab initio molecular dynamics for liquid metals[J]. Journal of Non-Crystalline Solids， 1995（192-193）： 222-229. doi： 10.1016/0022-3093（95）00355-x.

[22] BLÖCHL P E. Projected augmented-wave method[J]. Physi⁃cal Review B， 1994， 50（24）： 17953. doi： 10.1103/PhysRevB.50.17953.

[23] PERDEW J P， BURKE K， ERNZERHOF M. Generalized Gradient Approximation Made Simple[J]. Physical Review Letters， 1996， 77（18）： 3865. doi： 10.1103/PhysRevLett.77.3865.

[24] HEYD J， SCUSERIA G E， ERNZERHOF M. Hybrid func⁃tionals based on a screened Coulomb potential[J]. Journal of Chemical Physics， 2003， 118（21）： 8207–8215 . doi： 10.1063/1.1564060.

[25] JU L， BIE M， TANG X， et al. Janus WSSe monolayer： an ex⁃cellent photocatalyst for overall water splitting[J]. ACS Ap⁃plied Materials amp; Interfaces， 2020， 12（26）： 29335–29343. doi：10.1021/acsami.0c06149.

[26] 廖雨洁. InTe 及其Janus 结构光电性质的第一性原理研究[D]. 湘潭： 湘潭大学， 2020.

[27] 樊洁平， 刘惠民， 田强. 光吸收介质的吸收系数与介电函数虚部的关系[J]. 大学物理， 2009， 28（3）： 24-25.

[28] 张加宏， 谢丽君， 陈虎， 等. 掺杂与应力对ZrO2薄膜电子结构和光学性质的影响[J]. 四川大学学报（ 自然科学版），2019， 56（6）： 1145-1150.

[29] 苏玉长， 肖立华， 伏云昌， 等. LaB6电子结构及光学性质的第一性原理计算[J]. 中国科学（物理学 力学 天文学），2011， 41（1）： 58-65.

[30] 郁玲玲. 基于第一性原理方法的一维两面神MoSSe/WSSe超晶格纳米带性能调控的研究[D]. 上海： 上海师范大学，2020.

[31] 孙志远， 唐梅， 张欣欣， 等. Li 掺杂单层Janus MoSSe 电子结构和光学性质的第一性原理研究[J]. 广西师范大学学报（自然科学版）， 2021， 39（6）： 130-139.

[32] AHMAD I， SHAHID I， ALI A， et al. Electronic， mechanical，optical and photocatalytic properties of two-dimensional Ja⁃nus XGaInY （X， Y ;= S， Se and Te） monolayers[J]. RSC Ad⁃vances， 2021， 11（28）： 17230-17239. doi：10.1039/d1ra02324a.

[33] 李苗苗， 王天兴， 夏存军， 等. Cu2ZnSnS4/Cu2ZnSnSe4 电子结构与光学特性的第一性原理计算[J]. 中国有色金属学报，2012， 22（5）： 1413-1420.

[34] 范梦慧， 岑伟富， 蔡勋明， 等. 3C-SiC 表面电子结构及光学性质的第一性原理计算[J]. 人工晶体学报， 2018， 47（7）：1346-1352.

【编校：许洁】

基金项目：四川省科技计划项目（2022NSFSC1817）；宜宾学院计算物理四川省高等学校重点实验室开放基金项目（YBUJSWL-ZD-2021-04）