脂肪肝和血脂异常二元响应混合效应模型及其应用

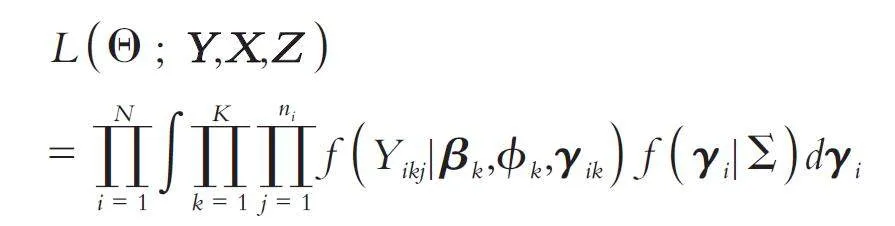
摘 要：为了探究脂肪肝、血脂异常与各常规体检项目间的关系，实现对脂肪肝和血脂异常的发病风险评估，基于2 972 例体检者9 091 人次血常规体检结果建立以脂肪肝血脂异常为响应变量的二元响应广义线性混合模型，并进行疾病风险预测以及预测效果评价. 结果表明：脂肪肝血脂异常的共同影响因素有性别、年龄、糖尿病、体质指数、谷丙转氨酶和高密度脂蛋白，脂肪肝和血脂异常两个响应之间的混合效应之间呈现一定的正相关性. 在模型预测方面，模型中脂肪肝的ROC 曲线下面积SAUC 为0.855（95%CI：0.831～0.881），血脂异常的ROC 曲线下面积SAUC 为0.814（95%CI：0.794～0.850），五则交叉验证结果显示脂肪肝血脂异常的SAUC 分别为0.850（95%CI：0.845～0.868）、0.807（95%CI：0.793～0.819），表明模型能够充分反映响应变量之间的相关性，具有较好的预测能力，适用于医学上多疾病的联合分析.

关键词：体检数据；脂肪肝；血脂异常；常规体检项目；多元广义线性混合效应模型

中图分类号：Ｏ212.1; R195

DOI： 10.19504/j.cnki.issn1671-5365.2024.06.16

随着人民群众生活水平的提高，健康意识不断增强，人们对健康体检与管理的需求呈上升态势[1-2]. 定期体检是一个必要的健康管理环节，通过定期进行体检了解自身的健康状况，对检查出的身体健康问题做出正确的干预，以预防或者控制疾病[3-4]. 人们饮食结构的改变使脂肪肝、血脂异常患者人数逐年增加[5]， 但脂肪肝的可逆性以及血脂异常状态可改变，使得正确干预下有效减少肝硬化或肝癌以及心血管疾病的发生成为可能[6-8]. 对疾病的相关性分析多集中在一个响应变量的相关性分析，如通过建立逻辑回归模型分析某一个疾病与其他指标的相关关系，实际上单个疾病响应变量并不能全面描述个体情况，因此，为了更加全面地刻画变量之间的相关关系，需要研究多元响应的回归建模问题. 医院采用信息化技术积累了大量的医疗数据[9-11]，对这些数据所蕴含的意义尚需进一步分析挖掘. 在体检过程中，通常会对同一个体进行多次检查，包括对血压、心率、血液、体重等多个指标的测量，以监测个体健康状况的变化，因此体检数据是一种纵向数据（统计学中指在不同时间点对同一组个体或观察单元进行的重复测量或观察所得到的数据）.本文拟通过对重复测量的体检数据建立二元广义线性混合效应模型，以解释脂肪肝和血脂异常的患病率及影响因素，为脂肪肝血脂异常的防治提供参考.

1 数据来源

数据源自2006—2014 年间在某医院健康体检中心定期体检的2 972 例体检者9091 人次体检数据，共纳入19 项体检指标作为研究变量. 连续变量有：体质指数即体重身高2（kg/m2）、白细胞、血红蛋白、血小板、总胆红素、总蛋白、白蛋白、白球比、谷丙转氨酶、尿素氮、肌酐、高密度脂蛋白和低密度脂蛋白；分类变量有：性别（女性赋值1，男性赋值0）、年龄层（年龄lt;60 赋值1，年龄≧60 赋值0）、脂肪肝（依据腹部彩超检查结果判定体检者是否患有脂肪肝，是赋值1，否赋值0）、高血压[12]（收缩压≧140 mmHg或舒张压≧90 mmHg 赋值1，其余情况赋值0）、血脂异常[13]（高胆固醇血症（总胆固醇≧6.2 mmol/L）或高甘油三酯血症（甘油三酯≧2.3 mmol/L）的情况赋值1，其余情况赋值为0）、糖尿病[14]（空腹血糖≧7.0mmol/L 或餐后血糖≧11.1 mmol/L 赋值1，其余情况赋值0）.

2 模型理论

多元广义线性混合模型如下： 定义Yikj （i =1，2，…，N ; k = 1，2，…，K ; j = 1，2，…，ni ）是第i 个体的第k 个响应变量在时间点tij 处的观测，Yikj 可以是连续的也可以是离散的，是具有分散参数ϕk 的指数分布族，于是有：

g （E （Y ） ikj |Xikj，Zikj，γik ） = X Tikj βk + Z Tikj γik

其中： XXikj 是固定效应的p 维协变量，βk 是相关的p ×1 维参数向量，Z Tikj 是随机效应的q 维协变量，γik 是相关的q × 1 维参数向量，g 是一个单调连接函数，它取决于结果的类型（如二元结果连接函数是logit 函数）.随机效应γi = （γTi1，γTi2，…，γTiK ） T ～N （0，Σ），在此Σ不仅考虑了每个结果重复测量的相关性，还考虑了多个结果之间的关联. 值得注意的是，给定γik，随机变量Yik1，Yik2，…，Yikni 对于i 个体是独立的. 给定参数向量Θ = { } βTk，Σ，ϕkKk = 1，其似然函数为：

多变量的联合建模使用多变量广义线性混合模型进行，主要有两个优势：（1）连续和离散型的结果都可以联合同时分析，（2）多个响应结果之间的相关性可以纳入该模型. 模型参数通过贝叶斯方法进行估计，利用R 软件中的“MCMCglmm”软件包得到参数的估计和推断[15]，在“MCMCglmm”R 包的默认选项下，β 参数的先验分布为正态分布，协方差矩阵Σ 服从逆Wishart 分布，而弥散参数ϕ 为gamma 分布，这是无信息的. 另外，在参数估计过程中使用MCMC 算法，进行3 000 次burn-in 和1 000 次后续迭代（细化为1∶10），从联合后验分布中获得样本（使用“MCMCglmm”函数），将样本均值作为参数的估计.

3 结果

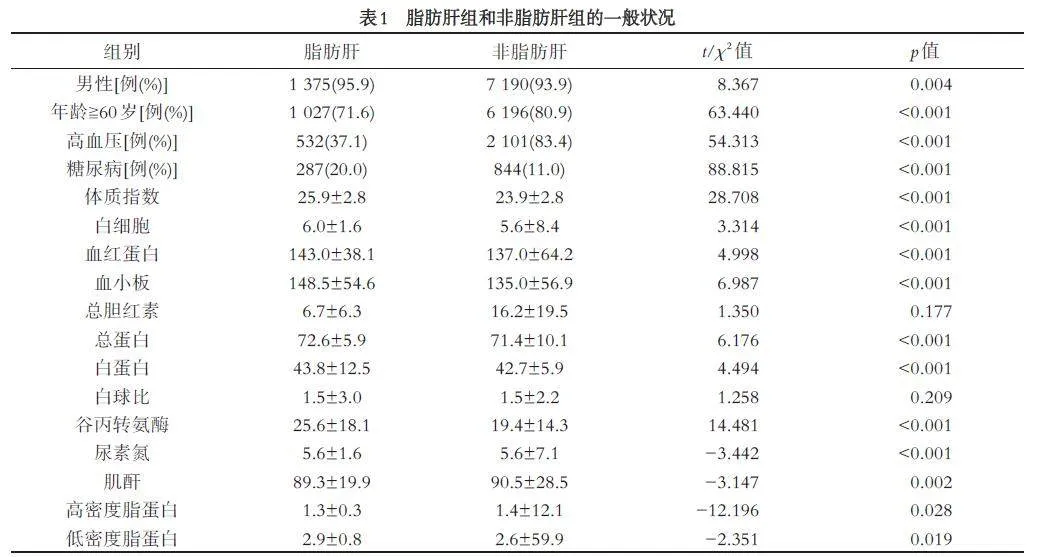
3.1 脂肪肝组与非脂肪肝组的一般状况

本研究中脂肪肝的检出率为15.77%（1434/9091），各年龄段人群中脂肪肝检出率分别为非老年组21.79%（407/1868）和老年组14.22%（1027/7223），随着年龄的增加，脂肪肝的检出率下降（χ2 = 63.44，p lt; 0.001）.脂肪肝组的男性比例、糖尿病比例、体质指数、白细胞、血红蛋白、血小板、总蛋白、白蛋白、谷丙转氨酶和低密度脂蛋白高于非脂肪肝组，脂肪肝组的老年比例、高血压比例、肌酐和高密度脂蛋白低于非脂肪肝组（见表1）.上述结果表明男性、糖尿病、体质指数过高等均是引发脂肪肝疾病的因素，并且较高的谷丙转氨酶和较低的高密度脂蛋白也会诱发脂肪肝.

3.2 脂肪肝血脂异常与常规体检项目相关关系

为了更加准确地分析脂肪肝血脂异常与体检项目相关性，以及脂肪肝和血脂异常之间的相关关系，利用联合建模方法对脂肪肝和血脂异常进行综合分析，建立联合模型：

log it （Pr （Y ）） ikj = 1| γik = X Tikj βk + γik，（i = 1，…，2972 ; k = 1，2 ; j = 1，…，9）

这里的响应变量脂肪肝和血脂异常均是二分类的，于是选择的连接函数为log it 函数. 考虑的协变量有性别、年龄分组、血脂异常、糖尿病、体质指数、血小板、总胆红素、白蛋白、谷丙转氨酶、肌酐、高密度脂蛋白和低密度脂蛋白，考虑的随机效应的协变量为个体变量（仅考虑随机截距不考虑随机斜率），其中，个体之间是通过体检者唯一id 标识变量进行识别匹配的.

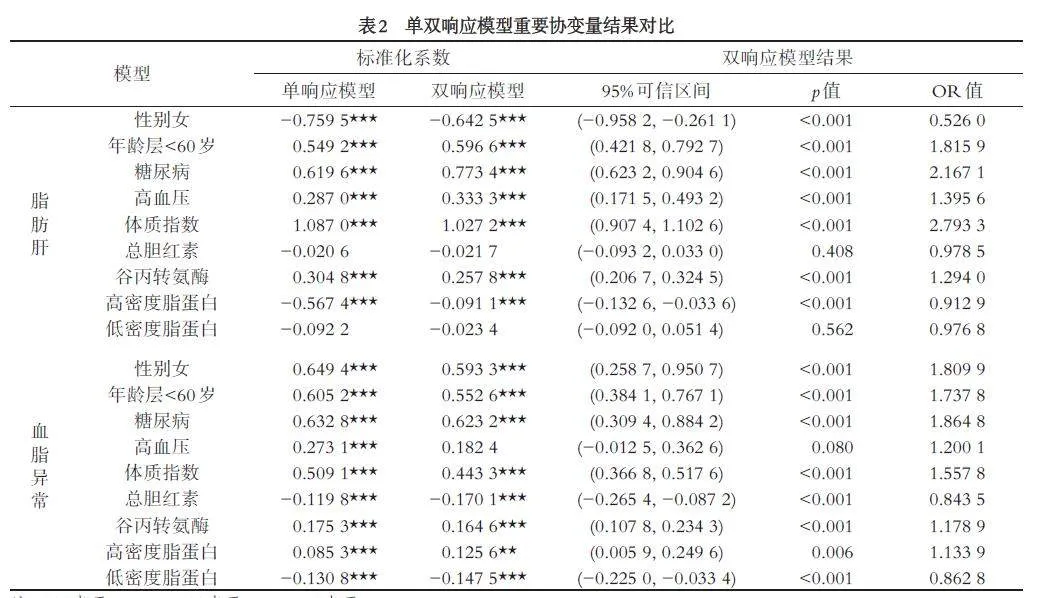
表2 展示了模型中重要协变量估计结果. 对于双响应模型脂肪肝和血脂异常而言，性别女的系数估计值分别为-0.6425、0.5933（p 值均lt;0.001），对应的OR 值分别为0.5260、1.8099，这说明性别间脂肪肝和血脂异常患病风险均具有显著性差异，男性更容易患脂肪肝，女性更容易患血脂异常，且女性患脂肪肝的风险仅为男性的50%，患血脂异常的风险却比男性高81%. 体质指数的系数估计值分别为1.0272、0.4433，对应的p 值均lt;0.001，说明随着体质指数的增大，脂肪肝和血脂异常患病风险均会显著增加. 总胆红素的系数估计值为-0.0217、-0.1701（对应的p 值分别为0.408、lt;0.001），说明总胆红素是脂肪肝的影响因素，而与血脂异常无关. 高密度脂蛋白的系数估计值为-0.0911、0.1256（p 值均lt;0.05），对应的OR 值分别为0.9129、1.1339，说明高密度脂蛋白是脂肪肝和血脂异常的共同影响因素，但是，较高的高密度脂蛋白是脂肪肝的保护因素，却是血脂异常的危险因素. 从其他变量的系数估计结果可以看出，对于脂肪肝患病风险而言，在其他影响因素相同的情况下，糖尿病、高血压患者的患病风险更大，脂肪肝患病风险与谷丙转氨酶的浓度呈正相关，与高密度脂蛋白呈负相关；对于血脂异常患病风险，显著的影响因素是年龄≦60 岁、糖尿病、谷丙转氨酶过高和低密度脂蛋白浓度过低等.

此外，表2 给出了对应的脂肪肝和血脂异常单双响应模型的重要协变量系数估计及其显著性. 就系数显著性而言，单双响应模型基本一致，因此无论是以脂肪肝和血脂异常作为响应变量的双响应模型还是分别以脂肪肝血脂异常为响应变量建立的单响应模型，对于脂肪肝血脂异常与常规体检项目的相关性认定是基本一致的.

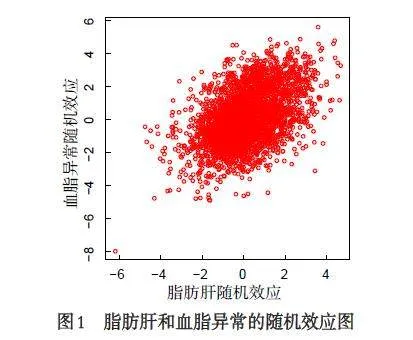
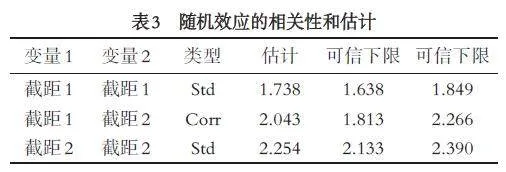
通过检验随机效应的显著性以及不同响应过程之间随机效应的相关性，以验证脂肪肝患病风险和血脂异常患病风险之间的相关性. 表3 展示了混合效应模型中随机效应的方差估计和相关系数估计，可以看出脂肪肝的随机效应和血脂异常的随机效应都是显著不为0（可信区间不包含0），而且脂肪肝的截距项随机效应和血脂异常的截距项随机效应具有显著的线性相关性（经计算相关系数为0.52）.图1是随机效应的估计散点图，从中也得出相同的结论，即脂肪肝和血脂异常之间存在一定的相关性，这个结论与一些文献报道的随着脂肪肝患病风险的增加、血脂异常发生率明显增高一致.

通过与对应的单响应模型对比分析发现，单双响应模型对于脂肪肝血脂异常危险因素的认定是基本一致的，但双响应模型通过利用随机效应的联合分布揭示了脂肪肝与血脂异常之间存在的正相关性（脂肪肝和血脂异常双响应模型计算出响应变量的随机效应之间的相关系数为0.52）.

3.3 模型的预测能力评价

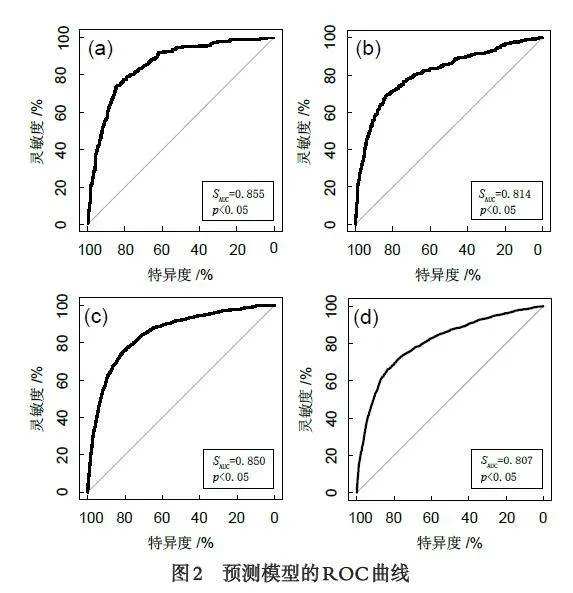
通过双响应模型分析可得脂肪肝与血脂异常的患病风险呈正相关，此结论符合实际意义. 为了进一步验证模型的适用性，对模型的预测能力进行深入分析. 预测模型的ROC 曲线如图2 所示，其中（a）、（b）为预测模型的脂肪肝和血脂异常ROC 曲线，脂肪肝预测模型ROC 曲线下面积SAUC 为0.855（95%CI：0.831～0.881）；血脂异常预测模型ROC 曲线下面积SAUC 为0.814（95%CI：0.794～0.850）.对模型进行五折交叉验证后的脂肪肝、血脂异常ROC曲线见图2 中（c）、（d），其脂肪肝、血脂异常预测模型ROC 曲线下面积SAUC 分别为0.850（95%CI：0.845～0.868）和0.807（95%CI：0.793～0.819）.预测模型与五折交叉验证得到的SAUC 差别不大，说明模型稳定性较好.

4 讨论

生物医学研究中产生的大量纵向数据，兼顾了横断面数据特性和时序性，同一变量的不同时间点之间存在相互关系，不同变量之间也存在某种关联，众多的变量和指标能够更加全面综合地反映个体特征，可为医学诊断、疗效评估等提供大量信息，医学分析价值极高[16]. 如何将这些信息和数据隐藏的规律剖析清楚，为医学研究提供有效帮助，是统计学致力于发展的核心问题. 实际应用中，根据数据特性和模型特点选择合适的统计方法，是得到可靠结果和充分利用数据信息的核心要件，是促进医学研究的有力保障. 本文采用广义线性混合效应模型对多元纵向数据进行单独建模和联合建模，探讨了联合建模的优势. 结果发现：年龄lt;60 岁、糖尿病、体质指数过高以及谷丙转氨酶过高会同时影响脂肪肝和血脂异常的患病率；高血压、血小板、白蛋白、尿素氮和肌酐只影响脂肪肝的患病率而与血脂异常无关；白细胞、血红蛋白、总胆红素、总蛋白、白球比和低密度脂蛋白只影响血脂异常的患病率而与脂肪肝无关.因此，定期进行体检，了解自身健康情况，能够及时发现问题并加以控制从而减少脂肪肝、血脂异常疾病的发生. 此外，二元广义线性混合效应模型通过利用随机效应之间的相关性来刻画不同的响应变量之间的相关关系，揭示了脂肪肝和血脂异常患病风险的正相关性，符合实际意义，具有参考价值. 在医学数据中，通常一个响应无法反映疾病全部情况，而多元响应模型通过随机效应之间的协方差矩阵来反映响应之间的关系，丰富了医学数据分析方法，为医学数据研究提供了新的思路，一定程度上可以推动医疗事业的发展.

参考文献：

[1] 张静波， 李强， 刘峰， 等. 健康管理服务模式的发展趋势[J].山东大学学报（医学版）， 2019， 57（8）： 69-76.

[2] 关宁， 段续微. 大数据环境下我国健康体检模式的发展与探究[J]. 中华健康管理学杂志， 2022， 16（9）： 644-646.

[3] 冷芬， 欧阳平， 张广清， 等. 新冠肺炎疫情对居民健康体检意愿的影响因素分析[J]. 护理学报， 2021， 28（12）： 49-52.

[4] 程树桃. 定期体检的必要性分析[J]. 中国保健营养， 2017，27（8）： 383.

[5] 苏海. 关于我国血脂异常患病率的几个问题[J]. 中华血脂异常杂志， 2018， 26（11）： 1001-1003.

[6] PARASCHIV A. Epidemiological evolution of chronic hepa⁃titis， liver cirrhosis and liver cancer in the Republic of Mol⁃dova[EB/OL]. （2021-04-01） [2023-03-25]. https：//api. se⁃manticscholar.org/CorpusID：233615444.

[7] ZHANG X， COKER O O， CHU E S， et al. Dietary choles⁃terol drives fatty liver-associated liver cancer by modulating gut microbiota and metabolites[J]. Cut， 2021（70）： 761-774.doi：10.1136/GUTJNL-2019-319664.

[8] 陈伟伟， 高润霖， 刘力生， 等.《 中国心血管病报告2016》概要[J]. 中国循环杂志， 2017， 32（6）： 521-530.

[9] 王美珊， 姚兰， 高福祥， 等. 面向医疗集值数据的差分隐私保护技术研究[J]. 计算机科学， 2022， 49（4）： 362-368.

[10] 于国庆， 沈飞. 数据挖掘技术在医疗大数据分析中的应用——评《医疗大数据分析与数据挖掘处理研究》[J]. 中国科技论文， 2022（7）： 847-847.

[11] HUANG W， HUANG D， DING Y， et al. Clinical applica⁃tion of intelligent technologies and integration in medical laboratories[J]. iLABMED， 2023， 1（1）： 82-91. Doi： 10.1002/ila2.9.

[12] GONZÁLEZ-VILLALPANDO C， Stern M P， Haffner S M，et al. Prevalence of hypertension in a Mexican population ac⁃cording to the sixth report of the Joint National Committee on Prevention， Detection， Evaluation and Treatment of High Blood Pressure[J]. European Journal of Cardiovascular Risk，1999， 6（3）：177-181. doi：10.1177/204748739900600309.

[13] 中国成人血脂异常防治指南修订联合委员会. 中国成人血脂异常防治指南（2016 年修订版）[J]. 中国循环杂志， 2016，31（10）： 937-950.

[14] 李静， 张毅强， 金萨茹拉， 苏敬. 糖尿病诊断标准再商榷[J].基层医学论坛，2018，22（8）：1110-1111.

[15] HADFIELD J D. MCMCglmm： Markov chain Monte Carlo methods for generalised linear mixed models[EB/OL]. （2010-02-10）[2023-03-25]. https：//citeseerx.ist.psu.edu/viewdoc/download？doi=10.1.1.160.5098amp;rep=rep1amp;type=pdf.

[16] DEBROUWER E， BECKER T， MOREAU Y， et al. Longi⁃tudinal machine learning modeling of MS patient trajectories improves predictions of disability progression[J]. Computer Methods and Programs in Biomedicine， 2021（208）： 106180.doi：10.1016/j.cmpb.2021.106180.

[17] 余昊， 赵超群， 杨建萍. 基于密度比模型的pAUC 半参数估计方法及其应用[J/OL]. 浙江理工大学学报（ 自然科学版）， 2023. https：//kns. cnki. net/kcms/detail//33.1338.TS.20230228.1656.014.html.

【编校：许洁】

基金项目：国家自然科学基金项目（U1830133）；中央高校基本科研业务经费项目（SWJTU，2682021ZTPY078）