深水清淤机械臂阀控液压油缸的加速干扰自适应滑模控制方法

樊帆，郑皓，史浩东，彭赛锋

（长沙矿冶研究院有限责任公司 深海矿产资源开发利用技术国家重点实验室，湖南 长沙 410012）

为解决江河湖库深水水域淤积问题［1-4］，长沙矿冶研究院借鉴深海采矿中的稀软底质作业技术［5］，开发一种适用于江河湖泊的集深水低扰动清淤、淤浆垂直提升为一体的水下环保清淤设备达诺1号［6］。达诺1 号搭载的清淤机械臂的阀控液压油缸系统在进行清淤作业时主要面临水下干扰大、手动控制精度低、阀控液压缸非线性特性导致的定位困难等问题［7］。

在阀控液压油缸这一领域，许多学者进行了控制策略以及控制率的研究。国外的Viet 等［8］设计低抖振滑模控制算法用于飞机起落架的可变阻尼器调节，并基于Simscape 平台进行实验测试验证该算法的改进效果。Feng等［9］针对液压机械臂的控制问题基于传统遗传算法设计其改进策略以寻找最优化的比例积分微分（proportional-integraliderivative，PID）控制器参数，试验验证该方法能有效提高液压机械臂的响应速度和控制精度。Kim 等［10］提出了一种结合滑模控制与时延控制的控制方法，该方法应用于陆地液压机械臂时的跟踪误差小于20 mm。国内的张义龙等［11］针对采煤机液压系统提出了前馈-反馈PID 复合控制方法，提高了液压系统的响应速度。秦永峰等［12］针对液粘调速离合器液压系统的低压工况需求的问题设计其泵阀的联合压力滑模控制策略，并通过仿真实验验证滑模控制策略相对于PID控制策略的强鲁棒性特点。徐国胜等［13］针对挖掘机的液压工作装置建立伺服液压系统的数学模型，设计基于高增益观测器的滑模控制方法以提高设备的控制稳定性和状态感知能力。才秦东等［14］就机械臂液压伺服系统存在的非线性特性和参数不确定性提出了一种自适应模糊滑模控制方法，仿真表明该方法使系统跟踪误差减小，响应速度加快。

本文针对达诺1 号清淤车清淤机械臂的阀控液压机构在水下清淤作业时面临的大扰动环境提出了一种加速干扰自适应的分层滑模控制方法，并使用李雅普诺夫（Lyapunov）稳定性理论［15］验证了该控制方法的稳定性。最后基于Simscape 多物理域仿真平台对该控制方法进行了大未知扰动下的位置跟踪试验，并与其他控制方法进行比对验证了该方法的有效性。

1 阀控非对称液压缸理论模型研究

如图1 所示为针对深水复杂环境的清淤车达诺1号，其工作装置由3个液压油缸驱动的连杆机构及一个由液压马达驱动的旋转绞吸头组成，通过各机构的协同高精配合以完成预期路径的清淤工作。

图1 达诺1号清淤车Fig.1 Dredging crawler of DreRo-I

如图2 所示为达诺1 号工作装置的液压连杆机构的连接关系，各机械结构之间为铰接关系，3 个共液压源的液压油缸分别驱动机械臂的底座、支臂与摆臂做围绕各自关节中心的旋转运动，因此液压油缸控制的准确程度、响应速度以及抗扰动能力直接决定了该工作装置于深水复杂环境清淤能力的好坏。

图2 工作装置液压连杆机构Fig.2 Hydraulic linkage of working device

清淤车上搭载的阀控非对称液压系统组成如图3 所示，由液压泵产生的液压动力源经由比例电磁阀控制阀口开度与方向后，作用到非对称液压缸的腔体内，驱动负载执行相应动作。其中，控制电压由控制器的放大电路产生，带动比例电磁阀阀芯产生位移后，电磁阀允许油源压力进入。液压缸的推杆上装有磁制位移传感器，可以将液压推杆的位移信号稳定精准地传回。

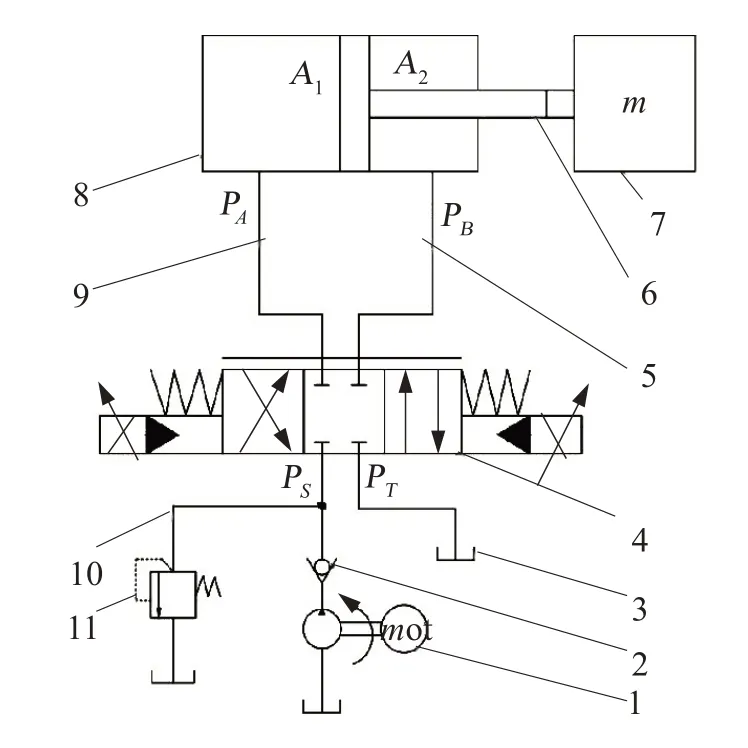
图3 阀控非对称油缸模型Fig.3 Valve controlled asymmetric cylinder model

1.1 比例电磁阀阀芯动态特性

参考相关文献［16-17］的设计方法，比例电磁阀的电控阀芯运动可以考虑为一阶惯性系统，则阀芯的动态特性为：

式中：T为伺服阀芯的时间常数；Kv为阀芯增益；u为控制电压；xv为阀芯位移。

1.2 阀控非对称油缸流量特性

在阀控非对称液压缸系统中，由于缸体面积不等，因此需要对缸体的正向及负向运动的流量特性分别研究。根据流体力学，当xv＞0 时流入液压缸左右腔的流量为：

式中：Q1为左腔流量；Q2为右腔流量；cd为伺服阀阀口流量系数；w为阀节流口面积梯度。

当xv＜0时，流入液压缸左右腔的流量为：

式中：ps为阀进口压力；pA为油缸左腔压力；pB为油缸右腔压力。

定义负载压力pL为：

省去中间推导步骤，可得负载流量QL为：

根据《液压控制系统》［18］，负载流量QL可线性化为：

式中：Kq为流量增益；Kc为流量压力系数。

根据液压缸腔体体积不变原理，最终整理可得阀控非对称油缸的流量连续性方程为：

式中：x为油缸位移；Vt为缸内有效容积；βe为液体弹性模量；Ct为泄露系数。

1.3 动力机构平衡方程

液压油缸的推杆在工作中主要受油缸的黏性阻力、负载惯性力及多因素下的干扰力等，因此将动力学平衡方程建立为：

式中：m为负载质量；B为运动阻尼；K为刚度系数，F为外干扰力。

1.4 阀控非对称油缸运动微分方程

由式（7）建立负载压力pL与阀芯位移xv的传递函数为：

一般情况下，油缸参数满足以下关系：

从频域角度分析可知负载压力pL对阀芯位移xv响应的截止频率高，具体情况为低频保真响应，高频响应截止，且液压缸的运动过程中阀芯位移xv的变化普遍为低频变化且受到一阶惯性系统的对高频信号的滤波作用，因此考虑进一步将式（7）简化为：

联立式（1）、（7）、（8）可整理得系统的动态运动微分方程为：

进一步将式（12）整理为状态方程的形式：

2 电磁阀控液压缸干扰自适应分层滑模控制器设计

下面由式（13）使用反步法进行液压缸的干扰自适应滑模控制器设计，并通过Lyapunov 稳定性理论，进行控制器的自适应补偿项设计和控制器的稳定性验证。控制流程如图4所示。

图4 控制器控制流程Fig.4 Controller control flow

2.1 虚拟力控制量设计

定义油缸位移的控制误差和滑模函数s为：

对s求导得：

取Lyapunov函数：

对V1求导：

定义虚拟力控制量α为：

因此可将α设计为：

将式（19）代入式（17）得：

干扰力误差的存在将是导致系统失稳的主要因素，接下来对干扰项进行自适应设计。

2.2 加速RBF神经网络干扰项自适应设计

经Park 等［19］通过数学证明，径向基函数神经网络（radial basis function neural network，RBF）具有万能逼近特性，因此本文采用RBF 神经网络对未知干扰项Fd进行逼近，并改进逼近方法，设计加速逼近率改善神经网络的逼近速度。

建立用于估算干扰项Fd的RBF 神经网络算法为：

式中：x为网络输入；j为网络隐含层节点序号；为网络的高斯基函数；W*T为网络的理想权值矩阵；ε为网络的逼近误差且满足关系|ε|≤εmax。

本文取神经网络的输入层为[x1x2]T，则自适应干扰估计值为：

定义干扰的观测误差为：

取Lyapunov函数：

对V2求导：

当设计参数满足η＞|ε|max时：

据Lyapunov 稳定性理论，系统渐近稳定，但干扰估计的收敛速度不可控。

为加快干扰的估计速度，增强控制器对低频变化干扰的适应能力，接下来对干扰观测矩阵的自适应律进行改进。

理想情况下，υ与滑模函数s的关系需要满足如下条件：

上述描述中，δ为0.01左右的极小正常数。

以上述期望性能作为设计依据，最终可将观测速度υ设计为：

当设计参数υmax取20，kυ取100 时，该函数的特性曲线如图5所示。

图5 υ特性曲线Fig.5 Characteristic curve of v

由图5 知，设计的收敛速度项υ具有特性：滑模量s接近0 时干扰观测矩阵停止更新，当滑模量s增加（或减小）超过一定阈值后，激活干扰观测矩阵的更新，同时干扰观测矩阵的收敛速度限制为有限值。该项既保证了干扰观测项对稳态误差的快速逼近特性，同时也避免了当滑模量s在0值左右时干扰观测项的无效抖振。

式中λv＞0,ηv＞0。

取Lyapunov函数：

对V3求导：

2.3 基于负载压力观测器的模型修正

在前面研究基础上，将基于名义逆模型的负载压力观测器设计为：

使用该负载压力的观测值可得修正后的流量增益系数为：

由式（13）得修正后的a3值为：

由式（18）阀芯位移的虚拟控制量为：

2.4 控制器电压设计

本节目标为通过设计合适的控制电压，实现阀芯位移xv对阀芯位移虚拟控制量xvd的准确快速跟踪，实现对液压油缸的分层控制，由式（13），电压与阀芯的关系为：

定义阀芯的跟踪误差为：

设计控制器电压为：

3 基于Simscape平台的多物理域控制仿真

本节将使用Simscape 平台［20］搭建电磁阀控液压系统的单缸模型，并使用该模型进行大未知干扰下的连续阶跃信号跟踪与低频正弦信号的跟踪控制试验。Simscape 是基于Matlab 软件的多物理域系统的建模仿真平台，组件之间使用物理连接，包括机械、电气、液压和其他物理域。可以使用它提供的各物理域基础模块来组装各种物理模型，并将其用于开发控制系统和测试系统级性能。

清淤机械臂工作装置使用的油缸模型如图6所示。

图6 油缸模型Fig.6 Cylinder model

根据达诺1 号深水清淤车清淤工作装置的实际作业工况，给出系统的主要标称参数如表1所示。

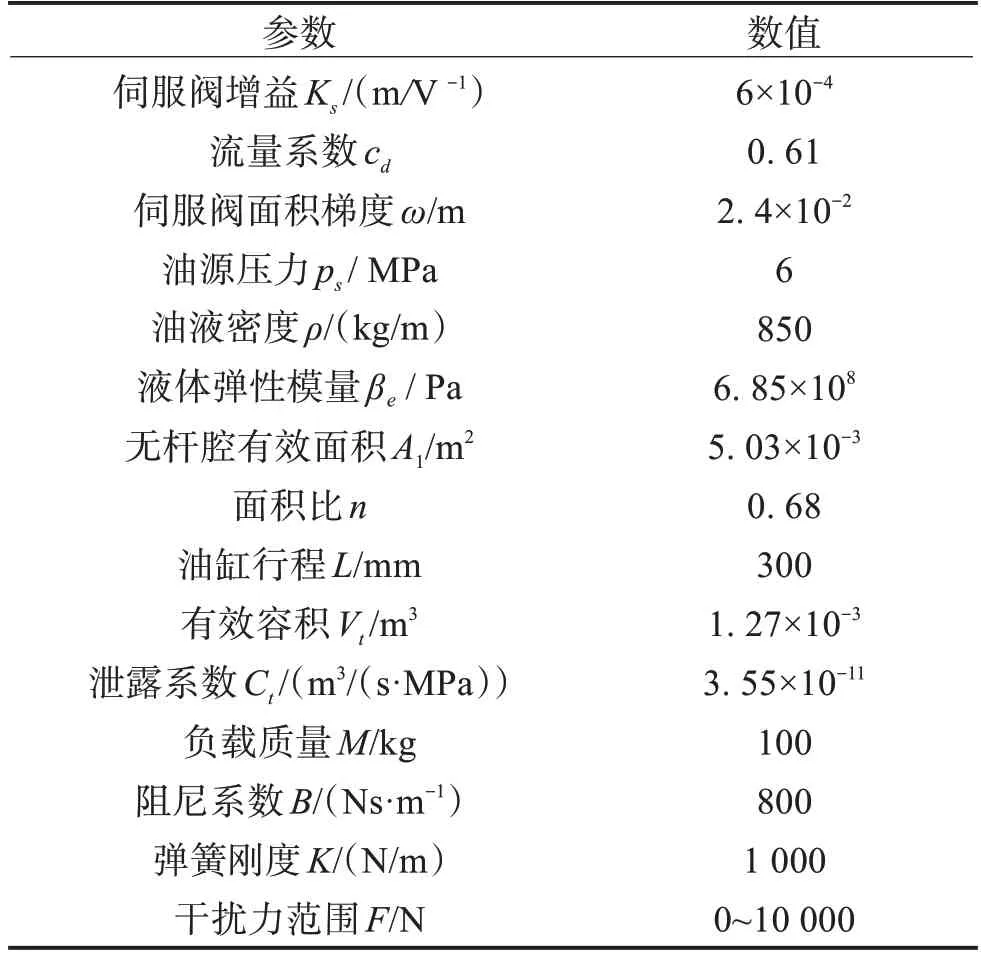
表1 清淤车液压工作机构主要参数标称值Table 1 Nominal values of main parameters of hydraulic working mechanism of dredger

参与仿真的模块主要包括油缸位移信号模块、液压油缸Multibody模块、阀控液压系统模块、液压泵模块以及滑模控制器模块等。控制的期望路径由油缸位移信号模块产生，信号输入滑模控制器后控制器输出合适的电压驱动比例电磁阀调整阀开度，进而带动液压油缸做出运动，仿真回路中各模块均为物理连接，仿真中反馈信号由Simscape内置的传感器采集。各模型在Simscape上的连接关系如图7所示。

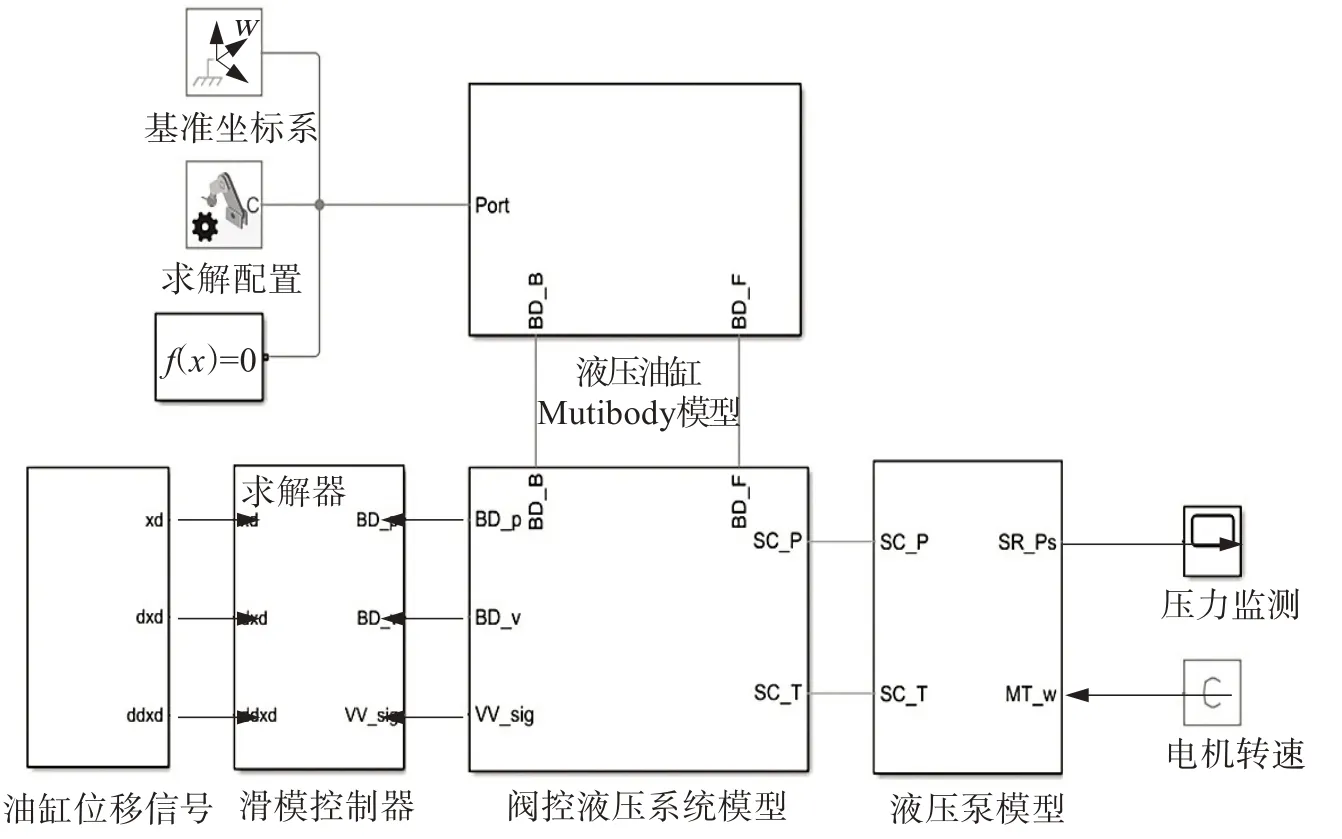
图7 多物理域油缸控制仿真模型Fig.7 Simulation model of multi-physical domain cylinder control

为验证本文提出算法的改进效果，将分别选用加速干扰自适应滑模控制器、干扰自适应滑模控制器以及经过优化调参后PID控制器分别进行液压油缸的位置信号跟踪控制仿真试验，同时为检验设计的控制器对大干扰力的适应能力，仿真中将在控制油缸运动的第4 s对油缸推杆施加6 000 N的阶跃力学信号，通过观察控制下油缸的位移响应来评价不同控制器的自适应能力。

在0.2 m 的阶跃信号下，10 s内不同控制器下的油缸对阶跃信号的响应情况如图8所示。

图8 油缸阶跃信号跟踪情况Fig.8 Tracking of step signal of oil cylinder

为进一步验证不同控制器对动态位移信号的跟踪能力，设置目标位移跟踪曲线为幅值0.14 m，周期15.71 s 的正弦位移信号，一个周期时间内不同控制器作用下的油缸响应情况如图9所示。

图9 油缸正弦信号跟踪情况Fig.8 Tracking of sinusoidal signal of oil cylinder

由图8 和图9 知，在对阶跃信号的追踪中，本文设计的加速干扰自适应滑模控制方法相比于传统PID 控制器具有响应速度快，稳定速度快，几乎无超调量的特点；相比于普通干扰自适应滑模控制方法具有稳态误差更小，调整速度更快的特点，且由图8（c）与图9（c）知，加速干扰自适应滑模控制方法对干扰的变化更加敏感，且对干扰值得估算速度更快，有利于增强系统的抗干扰能力。

4 结论

1）本文针对达诺1 号搭载的深水清淤臂阀控非对称液压油缸电磁阀控位置系统存在的高阶非线性特性以及液压油缸工作时面对未知大扰动的问题，提出了一种加速干扰自适应滑模控制方法并使用Lyapunov稳定性理论验证了其稳定性。

2）该方法能对液压油缸的负载变化进行快速有效地估算，并将估算结果用于控制器的前馈补偿和液压系统流量特性的数据修正，增强了控制器的干扰抵抗能力和控制效率。

3）基于Simscape 平台的机电液多物理域联合仿真结果表明，提出的加速干扰自适应滑模控制方法能够实现对预期油缸位移的准确快速追踪，且相比于普通干扰自适应滑模控制方法和PID 控制方法，加速干扰自适应滑模控制方法的稳态误差更低，且受到未知大干扰力的影响程度更小，重新调整回正的用时更短。