基于齐次系统理论的多船有限时间饱和包容控制

马俊达，谭冲，范佳佳

（1.哈尔滨理工大学 自动化学院，黑龙江 哈尔滨 150001；2.黑龙江省复杂智能系统与集成重点实验室，黑龙江 哈尔滨 150001）

近些年来，多船编队控制已经成为海洋工程领域的热点研究方向。相比于传统单船作业，由多船相互协作构成的编队系统具有生存能力强、运行成本低、作业半径大等优点［1］。在实际工程领域，船舶编队协同作业存在着应用场景多变、集结时间有限以及控制输入受限等实际问题。因此，在考虑水面船的实际物理约束情况下,如何进一步扩展编队的应用场景,实现多船有限时间内的快速集结是横亘在船控专家面前的首要难题。

在应用扩展方面,早期多船编队理论研究主要围绕队形生成［2］、无领导者法［3］以及领导者-跟随者法等方面开展，近几年逐步聚焦于以多领导者为编队特点的包容控制［4-6］。以往编队控制方法存在2种设计思路：一种是以领导者-跟随者法为代表，基于非线性控制理论，将编队控制问题转化为闭环系统的镇定问题；另一种则以队形生成和无领导者为代表，以图论为数学理论基础，强调编队生成过程中的状态一致性，近期相关研究更突出第2 类。有别于领导者-跟随者法队形由单一领导者确定，包容控制需多个领导者。在实际工程应用中，搭配高性能传感器的船舶可以探测更大范围水域信息，可作为船舶编队系统中的领航船，其他船舶仅需与这些领航船通信，利用多个领航船和邻船的状态信息设计分布式控制律实现跟随船收敛于领航船张成的区域内，最终跟随船可随领航船进行远洋探测作业。Peng［4］针对船舶易受到风浪流外部扰动的问题，利用基于预估器的神经网络动态面控制算法，分别设计了基于状态反馈和基于输出反馈2 种鲁棒包容控制律；Gu［5］结合扩展观测器、线性跟踪微分器和辅助变量法，面向基于参数化路径的多虚拟领航船，实现了欠驱动船舶鲁棒包容控制；Zhu［6］利用动态面控制技术,结合有限时间扰动观测器提出了一种具有抗干扰特性的包容控制策略。上述成果均以反步法为设计框架,将步骤分为运动学回路设计和动力学回路设计2 部分,并结合Lyapunov 稳定性理论实现包容控制，但控制效果高度依赖惯性矩阵和科里奥利向心力矩阵的参数取值准确性。因此，设计一种具备简化形式的多船包容控制律，降低对船模参数的依赖极具工程价值。

在时间优化方面，收敛速度也是衡量编队系统动态特性的重要技术指标。目前，多船包容控制算法大多仅实现了闭环系统的渐近稳定，较少考虑在有限时间内实现控制目标。然而实际海洋应用中,多船编队系统在有限时间内完成快速集结,不仅可提高系统动态响应速度,而且还可提升系统的抗干扰能力［7］。以齐次系统理论和有限时间稳定性理论为依托,多智能体有限时间控制已取得一定成果,但受限于船模的非线性特征,船舶有限时间编队控制成果较少。通过引入终端滑模，Li［8］将多船编队控制问题转化为有限时间镇定控制问题；Fu［9］研究了外部扰动下的多船编队控制问题，通过引入扩张观测器,实现了对系统状态和外部扰动的快速估计和补偿；李莉莉［10］利用障碍Lyapunov 函数实现对纵向速度和艏向角的约束，通过引入功率积分器保证欠驱动水面船有限时间路径协同。上述算法思路均通过定义编队控制偏差，并结合有限时间稳定性理论保证闭环系统的有限时间收敛,且不涉及齐次系统理论，其根本原因在于齐次系统理论对模型特性要求较高，不便直接应用。因此，基于齐次系统有限时间理论，针对船舶非线性模型研究多船有限时间包容控制问题是值得探究的。

在物理约束方面，饱和控制也是多船编队需要重点考虑方面，其性能的优劣直接影响着控制效果。多船编队控制中需要与其他船舶完成信息交互，往往造成初始偏差信号较大，进而超过执行器能够提供的最大力或力矩。为解决此问题，Xia［11］引入辅助动态系统，将辅助变量引入运动学和动力学回路的偏差向量，实现了对控制输入的限幅；林安辉［12］则通过在运动学回路设计中主动引入饱和函数约束编队偏差变量,从而限制了编队控制输入。近年来,以典型线性模型为研究对象的多智能体有限时间包容控制取得了一定进展。Zhao［13］针对二阶系统提出一种输出反馈的有限时间包容控制律，并基于有限时间稳定性理论证明闭环系统的稳定性；李玲玉［14］利用图论和齐次系统理论，设计一种基于扰动观测器的有限时间鲁棒包容控制律，实现了对不匹配干扰的在线补偿。上述成果针对模型相对简单,且并未考虑控制输入的有界性。

本文针对多领导者船舶编队控制问题，以三自由度非线性船舶模型为研究对象，基于齐次系统有限时间稳定性理论，充分考虑控制输入受限，提出了一种简化形式新型多船包容控制方法，创新点归纳如下：1）区别于以往多船包容控制律需获得精确惯性矩阵和科里奥利向心力矩阵参数,本文提出一种模型参数低依赖、具备简化数学形式包容控制律；2）不同于文献［11-13］基于Lyapunov 有限时间稳定性理论证明闭环系统的稳定性，本文基于齐次系统稳定性理论实现了闭环系统有限时间内的快速收敛；3）考虑了输入约束下的包容控制问题，通过引入饱和约束函数提出了基于包容位置偏差约束和速度约束的有限时间饱和控制律。

1 知识预备与问题描述

1.1 代数图论

假定n+m艘船间的通信可用图G=(V,E,A)表示，其中V={v1,v2,…,vn+m}表示节点的集合；E⊆V×V表示边的集合；A=[aij]∈ R(n+m)×(n+m)表示该图的邻接矩阵。有向边(vi,vj) ∈E表示vj可从vi获取信息。定义Ni={vj∈V|(vi,vj)∈E}为节点vi的邻居矩阵。当vj∈Ni时，aij=1，否则aij=0。对于所有节点，令aii=0。若对于∀i，有aij=aji，则图为无向拓扑图，且其邻接矩阵为对称阵；反之，图为有向拓扑图。图G的Laplacian阵L={lij}定义为：

定义1［15］对于∀j(i=1,2,…,n+m)有aij=0，则船i称为领导者；若存在j有aij=1，则称船i称为跟随者。

定义2［16］设集合X={x1,x2,…,xn}是实向量空间Rn的子集，集合X的凸包定义为：

1.2 有限时间稳定性理论与判据

定义3［17］考虑以下系统：

式中f:U→Rn为定义域U到R的向量函数。若对于任意ε＞0 有(r1,r2,…,rn) ∈Rn,ri＞0,使得函数f(x)满足：

式中：i=1,2,…,n,k≥-max {ri,i=1,2,…,n},则称函数f(x)关于(r1,r2,…,rn) 具有齐次度k。若f(x)是齐次函数，则称系统式(1)是齐次的。

引理1［17］考虑以下系统：

同时x=0 是系统式（3）的全局渐近稳定点，则x=0是系统式（3）的全局有限时间稳定点。

引理2［17］考虑如下系统：

若存在一个连续正定函数V(x) :U→ R 且c＞0,α∈(0,1),在U0⊂U的邻域上满足：

则V(x) 在有限时间内容收敛于0，且收敛时间满足T0＜V1-α(x(0))/c(1-α)。

引理3［18］考虑系统=f(t,x)，其中对于函数f(t,x) 满足f(t,0)≡0，并且系统存在唯一解。V(t,x) 和W(t,x) 在定义域上的连续函数并且满足如下条件：

1）V(t,x) 为正定非增函数；

3）|W(t,x)|有界；

1.3 船舶运动数学模型

忽略船舶横摇、升沉以及艏摇，则第i艘船三自由度非线性数学模型为［19］：

式中：ηi=[xi,yi,ψi]T为船i在大地坐标系下的位置向量；υi=[ui,vi,ri]T为船i在体坐标系下的速度向量；R(ψi) 为上述2 坐标系之间的转换矩阵；M、iCi(υi)、Di(υi)分别为船i的惯性矩阵、科里奥利向心力矩阵和阻尼矩阵；τi为船i的实际控制输入。为便于设计，令pi=ηi，qi=R(ψi)υi结合式(7)和式(8)得如下数学形式：

显然，上述数学模型满足如下性质：

1.4 控制问题描述

考虑多船编队中跟随船个数为n，分别标记为1,2,…,n；领导船数量为m，标记为m+1 至m+n。假设领导船为静止领导者，即动态特性满足：

式中：i=n+1,n+2,…,n+m；pi为领导船i的位置信息。假设所有跟随船至少有一艘邻居船,而虚拟领航船均没有邻居船。此时,多船编队通信拓扑结构满足如下假设：

假设1［20］假设由跟随船式（9）和式（10）构成的编队通信拓扑是无向连通的,任何一艘跟随船都有一艘虚拟领导船通过有向路径指向它,而领航船无需获取其他船的状态信息。

进一步，由n艘跟随船和m艘虚拟领导船构成的编队系统Laplacian阵L定义为：

式中：L1∈Rn×n为 跟随船间的Laplacian 阵；L2∈Rn×m为跟随船与领航船之间的Laplacian阵。

由定义2 和引理2 知，当位置向量XF趋近于Xd时，跟随船收敛于领航船张成凸包Co{pi,i=n+1,n+2,…,n+m},即实现了包容控制。

控制目标：考虑假设1，针对船舶模型式（9）和式(10)，利用其自身状态信息、邻船信息以及部分领航船信息设计具有输入饱和特性的有限时间包容控制律，使得跟随船在有限时间T0内收敛于领导船张成的区域内，即满足：

2 控制器设计与稳定性分析

基于包容偏差向量EX，结合代数图论、齐次系统理论以及饱和函数特性，n艘跟随船的有限时间包容控制律设计为：

式中：控制增益K1,K2＞0；0 ＜α1＜ 1；α2=2α1/ (α1+1)；sigα(x)=|x|αsgn(x)，sgn(x) 为 符号函数；SD1(x)=[sD1(x1),sD1(x2),…,sD1(x3n)]T为饱和函数向量；假设函数sD1:x→sD1(x)为连续奇函数，且满足：

1）|SD1(x) |≤D，D＞0；

2）x·SD1(x)＞0，x≠0，x∈ R；

3）在x=0 附近，有sD1(x)=cx+o(x),o(x) 表示x的高阶无穷小，且c＞0。

与之类似，SD2(x) 为饱和函数向量，同样满足上述3个条件。

定理1 对于具有模型式（9）和式（10）的n艘跟随船以及模型式（11）的m艘虚拟领导船组成的编队系统，若满足假设1，则跟随船在控制律式（13）作用下能够在有限时间内收敛于领航船张成的区域内，即满足控制目标式（12）。

证明 证明过程分4步：

1）将控制律式（13）代入式（9）得：

令Lyapunov函数为：

对式（16）两边同时求导得：

将式(14)代入式(19)可得：

将式(22)代入式(14)、(15)得：

式中：SD1(y)=CD1y+o(y)；SD2(y)=CD2y+o(y);CD1，CD2＞0；o(y)为y的高阶无穷小量。进一步整理式（24）可得：

结合式(23)和(25)可得：

其中：

针对如下系统：

进一步，将式(27)进行整理，并证明该是齐次且渐近稳定的：

令r1=1,r2=α1/α2,k0=(α1-1)/2,则有：

由上述分析知,系统式（28）关于(b1,b2,…,bn,bn+1,…,b2n)具有齐次度k0=(α1-1)/ 2 ＜0,其中b1=b2…=bn=1,bn+1=…=b2n=α1/α2。

3) 针对系统式(27)，构造Lyapunov函数为：

结合式(27)，对式(29)两边同时求导得：

由LaSelle 不变集理论可知,闭环系统式(27)在eX=0,VF=0全局渐近稳定。

4) 分析闭环系统式(26)非齐次项：

同时有：

综合式(31)和(32)可知：

根据引理1，综合步骤1)～步骤4)可知闭环系统式(26)在有限时间稳定，即eX=0,VF=0 是系统的全局有限时间收敛点。进一步，结合式(22)可知存在有限时间T0，使得当t→T0有XF+与VF=0，即实现控制目标式(12)。证毕。

注意 1）从编队控制律数学形式看，以往多船编队控制算法分完全模型依赖［2,6-12］和部分模型依赖［3-5］2 类。完全模型依赖需要获得包括Mi,Ci(υi),Di(υi)在内的准确船体准确模型参数，这对系统辨识精度提出了挑战；部分模型依赖往往利用神经网络技术在线估计模型参数和外界干扰，但需要计算量较大，且往往也需获取Mi或Ci(υi)精确值。本文提出控制律式(13)无需惯性矩阵Mi和Ci(υi)，在简化控制律数学形式的同时，实现了有限时间收敛。

2）文献［7-10］均利用Lyapunov 有限时间稳定理论开展多船有限时间编队控制研究，并未涉及齐次系统理论。由于齐次系统有限时间理论对研究对象的模型数学形式要求较高，一般非线性模型不能直接使用。针对此问题，本文先将系统化为积分形式式(9)和式(10)，然后将动力学部分拆解为齐次项和非齐次项f1(eX,VF)+f2(eX,VF)，进而满足了引理1 的系统形式要求，最终基于齐次系统理论证明了闭环系统在有限时间内收敛。

3）在编队形成初期，偏差向量‖EX‖和‖VF‖数值往往较大，会超过船舶执行器的物理上限。因此，本文通过引入饱和函数约束其变化范围，更具工程价值。

3 多船包容控制仿真验证

为验证控制律式(13)效果，本文以Cybership2为跟随船验证模型。此时，控制参数K1=30,K2=40,α1=1/ 2,α2=2/ 3,D=1，约束函数sD(x) 为：

式中：常数D＞0,显然|sD(x) |≤D。下面从2 种拓扑形式探讨编队控制效果。

3.1 对称拓扑结构下的多船包容控制

考虑编队系统由4 艘跟随船和4 艘虚拟领航船组成，其通信拓扑结构如图1所示。

图1 编队通信拓扑Fig.1 Communication topology

节点1～4 表示无向连通的跟随船1～4，节点5～8表示向跟随船单向传送的领航船5～8。假设通信拓扑中边的权重均为1，则系统Laplacian矩阵为：

显然由L2数学形式可知该通信拓扑结构为对称形式。

假设4艘跟随船的初始状态分别为：

4艘领航船的位置信息分别为：

图2～5为对称通信拓扑结构下的多船编队系统的控制效果。图2为4艘跟随船的运行轨迹,从中可看出跟随船收敛于4 艘虚拟船张成的矩形区域内；跟随船的位置偏差变量‖eXi‖=‖pi-pdi‖随时间变化曲线如图3。从图3中可看出,偏差信号在15 s内均收敛于0附近,即实现了有限时间内收敛的目标；图4 展示跟随船速度随时间变化曲线，即在15 s 内实现了速度收敛于0；跟随船在3个方向的控制输入随时间变化曲线如图5 所示。综上,包容控制律能够使得跟踪偏差在有限时间内收敛于0,即实现了控制目标式(12)。

图2 船舶运行轨迹Fig.2 Ship trajectory

图3 跟随船的跟踪偏差变化曲线Fig.3 Position tracking errors for each follower

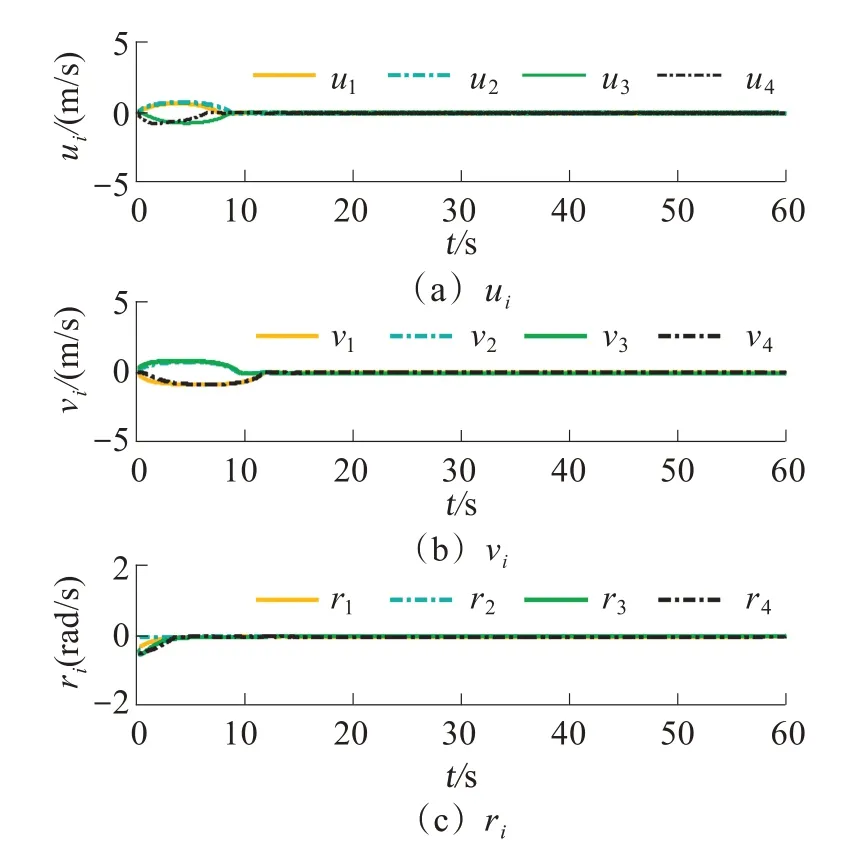
图4 跟随船的速度变化曲线Fig.4 Velocities for each follower

3.2 非对称拓扑下与其他方法比较

考虑编队系统由3 艘跟随船和3 艘虚拟领航船组成，取通信拓扑结构为非对称形式，具体结构如图6所示。

图6 编队通信拓扑Fig.6 Communication topology

其中节点1～3表示无向连通的跟随船1～3,节点4～6 表示虚拟领航船。假设通信拓扑中边的权重均为1,则系统Laplacian矩阵为：

本节将与文献［4］所设计的基于反步技术的多船包容法进行比较，其控制律为：

假设3艘跟随船的初始状态分别为：

3艘领航船的位置信息分别为：

在非对称通信拓扑结构下2 种控制算法的仿真曲线如图7～11 所示。图7、图8 分别为基于反步法和齐次法的船舶运动轨迹，可以看出2 种方法均可使跟随船收敛于领导船张成的三角区域内。图9以跟随船2 为例展示了2 种方法下的位置偏差变量‖eX2‖ 随时间变化曲线。从图9 中可看出齐次法相较于传统反步法具有更快的收敛速度，在10 s 内即可收敛于零。跟随船2的各个轴向速度随时间变化曲线如图10所示。2种方法的控制律随时间变化曲线如图11所示。从图11中可以看出，反步法在系统运行初期会产生较大控制幅值，甚至可能超过船舶执行器物理上限。本文所提出的基于齐次理论的包容控制算法通过引入约束函数，避免了初始跟踪偏差过大问题造成控制输入过大的问题。

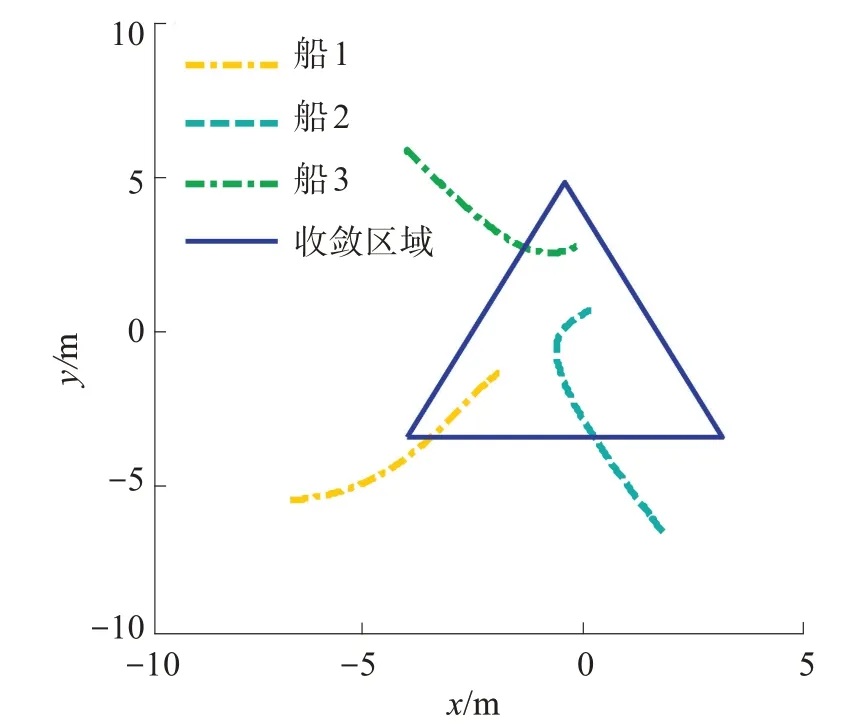
图7 基于反步法的船舶运行轨迹Fig.7 Ship trajectory based on backstepping method

图8 基于齐次理论控制法的船舶运行轨迹Fig.8 Ship trajectory based on homogeneous system the‐ory control method

图9 跟随船2的跟踪偏差变化曲线Fig.9 Position tracking errors for follower 2

图10 跟随船2的速度变化曲线Fig.10 Velocities for follower 2

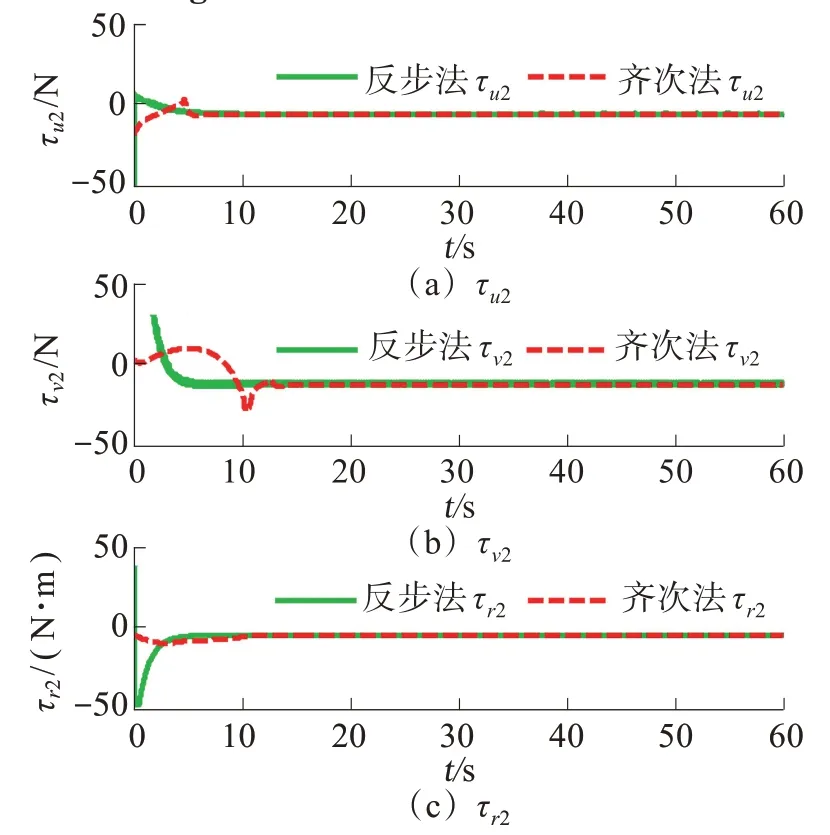
图11 跟随船2的控制律变化曲线Fig.11 Control inputs for follower 2

4 结论

针对多领导者船舶编队控制问题,本文提出了基于齐次系统有限时间稳定性理论的饱和包容控制方法，可得如下结论：

1）所提算法以齐次系统理论为基础，将系统化为由特定齐次项和非齐次项组成的数学形式，可简化控制律表达式，保证多船编队的快速收敛。

2）为规避初始跟踪偏差过大引发控制输入超幅的问题，本文利用饱和函数特性，结合图论相关知识，提出具有限幅特征的多船编队控制律。

3）未来将进一步研讨基于齐次系统理论的船舶输出反馈包容控制方法，并将结论延伸至其它多船编队控制形式。