内孤立波对海洋工程结构物作用的时空演变研究

刘倩，曾丽娟，崔健，欧阳佚卓，高俊亮，张瑞瑞

（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212100）

南海是我国的四大海域之一，是中国海域中面积最大、水深最深的海域。中国南海不仅面积位居榜首，而且石油、天然气资源的蕴藏量，也位居四大海域之首，被称作第2 个波斯湾［1-2］。但是中国南海的油气钻井作业环境也最为恶劣，不仅每年3～9 月受强烈的台风的袭扰，而且还拥有“独特”的海况——南海“内波”［3］。由于复杂的海洋环境和剧烈变化的海底地形，使南海尤其是南海北部内孤立波活跃，一直是内孤立波研究的热点海区［4-5］。南海北部海域的内孤立波振幅大、流速大，发生频率高，分布范围广，伴随着强烈剪切流，大幅度内孤立波会对海洋平台结构和钻井作业造成严重危害。近几年，由于内孤立波引起的海上作业安全事故时有发生，因此南海海域油气资源勘探开发过程中必须考虑内孤立波对海洋工程结构物的影响。

由于内孤立波在传播过程中携带的巨大能量对海洋工程结构物带来巨大的破坏，目前关于内孤立波对海洋结构物的载荷越来越受到人们的重视［6-9］。Cai 等［10］首次将Morison 的经验方法引入内波中，通过模态分解和回归分析等方法来估算内孤立波对小直径桩柱的作用力和作用力矩。叶春生等［11］在缺乏实测资料的情况下，采用Morison 公式计算了潮频及高频内波对直立桩柱的作用力。宋志军等［12］结合科特韦格-德弗里斯方程（korteweg-devries，KdV）理论和Morison 公式，计算了内孤立波对Spar 平台的作用力，结果表明内孤立波对海洋平台的稳定产生严重影响，并提出在平台的设计中要根据实际海况将内孤立波的影响考虑进去。Xie 等［13］采用连续分层非线性模型模拟内孤立波的产生，结合Morison方程计算了内孤立波和潮汐流共同作用下小直径桩柱的受力，结果表明无论内孤立波与潮汐流方向是否相同，考虑内孤立波后桩柱的受力都将远大于仅考虑潮汐流作用时的受力。LYU［14］基于二维非线性数值模型计算了内孤立波产生的速度场，并分析了背景水流对圆柱所受的力和力矩的影响。Zan 等［15］通过三维数值模拟计算了内孤立波诱导的流场大小，直接计算出假设的小直径桩柱的作用力大小，但是他们的研究缺乏实测数据的验证。目前世界范围内在海洋工程设施的设计标准和相关的平台设计软件中很少考虑内波的巨大作用力，并且大多数学者在研究内孤立波对桩柱作用力时大多只考虑了总体作用力，缺少对内孤立波荷载沿水深变化规律的探索。

本文利用南海北部陆坡区实测的高质量海流数据和温盐数据，应用 Matlab 软件，研究内孤立波对小直径桩柱的作用力的时空演变。作用力的计算分为2步，首先求内孤立波引起的速度场和加速度场，然后用Morison 方程和相应的经验系数计算作用力的大小。

1 潜标观测数据介绍

本文中的数据资料来源于2014年8月1日-2014年9月26日于南海北部东沙群岛附近的测站（如图1所示）采集的潜标数据资料，该测站位于（20.835°N，117.56°E）、848 m 水深处。潜标数据主要包括研究海域的流场数据、温度数据和盐度数据。

图1 南海北部测站位置Fig.1 Location of stations in the north of the South China Sea

图2 内孤立波对桩柱的作用力示意Fig.2 Schematic diagram of internal solitary wave acting on pile

为了获取海流数据，在该站位投放的潜标上设有2个声学多普勒流速剖面仪（acoustic Doppler cur‐rent profilers，ADCP）记录：一台观测姿态向上的WHS75K ADCP 系泊在500 m 深附近（有效数据从78～478 m）；另一台观测姿态向下的WHS75K ADCP系泊在520 m 深的附近（有效数据从553～825 m），2个ADCP 的时间间隔均为2 min，深度间隔均为16 m。

温盐数据通过布置在110、130、140、150、160、170、210、230、250、270、290、320、370、420、470、550、600、650、750、830 m 深处的温盐仪测量，有效数据位于110～830 m 水深，深度间隔沿着水深方向变大，水面附近处温度变化较大，深度间隔较小，海底附近温度变化不大，深度间隔较大。温盐仪的时间分辨率为15 s和10 s。

该测站获得海流数据覆盖了80%以上的水深，温度和盐度数据覆盖了90%以上的水深，数据质量高，提供了较完整的垂直剖面数据。

2 内波的模态分解和Morison方程

2.1 内波的模态分解

实际海洋中观测到的内波可以看成各个模态内波的线性叠加。这种模态分解仅依赖于浮力频率的垂直剖面N(z)，因而很容易通过所观测的密度剖面得到。基于线性内波的运动方程，内波引起的垂直位移可以由下列本征值方程以及边界条件确定：

式中：n=1,2,…为模态数；cn为本征速度。而内波斜压模态对于水平速度的垂直结构Π(z) 为：

在实际计算中，能够利用数值方法求解微分方程式(2)，从而得到内波各个模态的归一化振幅以及水平速度的垂直结构。

模态对应的斜压速度u′(z,t)为：

2.2 Morison方程

当结构物的直径D与入射波长L满足D/L＜0.15时，可以忽略结构物对波浪场的影响［9］。而内孤立波的波长通常能达到几百米乃至上千米，对于一般的结构物都能满足Morison 公式的适用条件，可以用Morison 公式计算内孤立波的作用力［12］，任意水深位置处作用于结构上的流体力主要由拖曳力fD和惯性力fI2个部分组成：

式中：拖曳力是由波浪水质点运动的水平速度引起的对结构物的作用力，其大小与水平速度的平方成正比；惯性力是由波浪水质点运动的加速度引起的对结构物的作用力，与水质点的加速度成正比，表达式为：

式中：u和分别为任意水深处流体质点运动的水平流速和加速度；CD为阻力系数；CM为惯性系数；D为桩柱的直径；ρ为流体的密度。

内孤立波对桩柱的作用力合力为：

3 实测内孤立波演变特征

从图3 可以看出，观测海区的密度和浮力频率在上层200 m 左右变化较大，200 m 以下，海水的密度和层结变化较小。

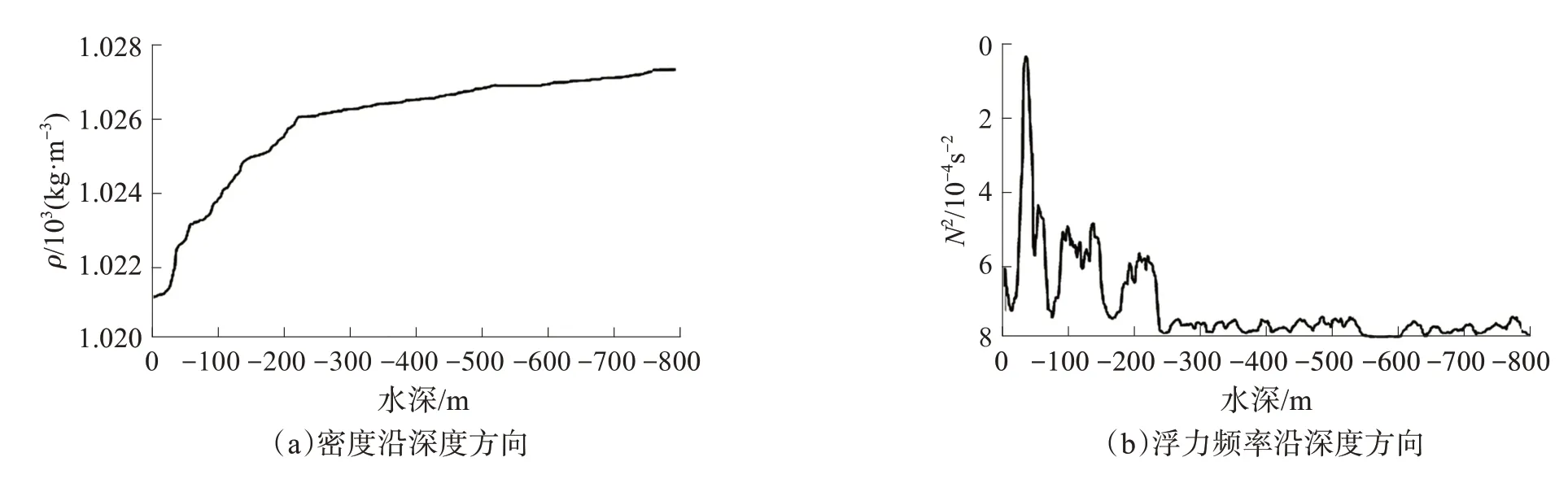
图3 密度、浮力频率沿深度方向的变化Fig.3 Variation of density and buoyancy frequency along the depth direction

图4 2014年8月11日观测到的内孤立波Fig.4 Internal solitary wave observed on August 11th,2014

内孤立波在传播过程中会引起等温度面的上下起伏，通过对实测数据的分析和处理，本文选取2014 年8 月11 日记录到的振幅最大的内孤立波作为研究对象，在该时间段内内孤立波的原始流速和等温线的时间-深度剖面图如图 4所示。

内孤立波经过时，水平流速存在最大值，最大水平流速可达1 m/s；垂向流速的方向会发生改变，并且取得最大值，最大值大约为0.2 m/s，相比于水平流速，垂向流速的量值明显较小，这与内孤立波的传播方向相对应。

8 月11 日7∶40-9∶20 时间段内内孤立波的原始流速和等温线的时间-深度剖面图，如图 5所示。

从图5 可以看到，该内孤立波以单个内孤立波的形式出现，内孤立波的传播周期T等于40 min，内孤立波达到时位于120 m水深附近处20℃等温线的上下起伏大约80 m，可以得到内孤立波的振幅A大约为80 m，远远大于表面波的振幅。

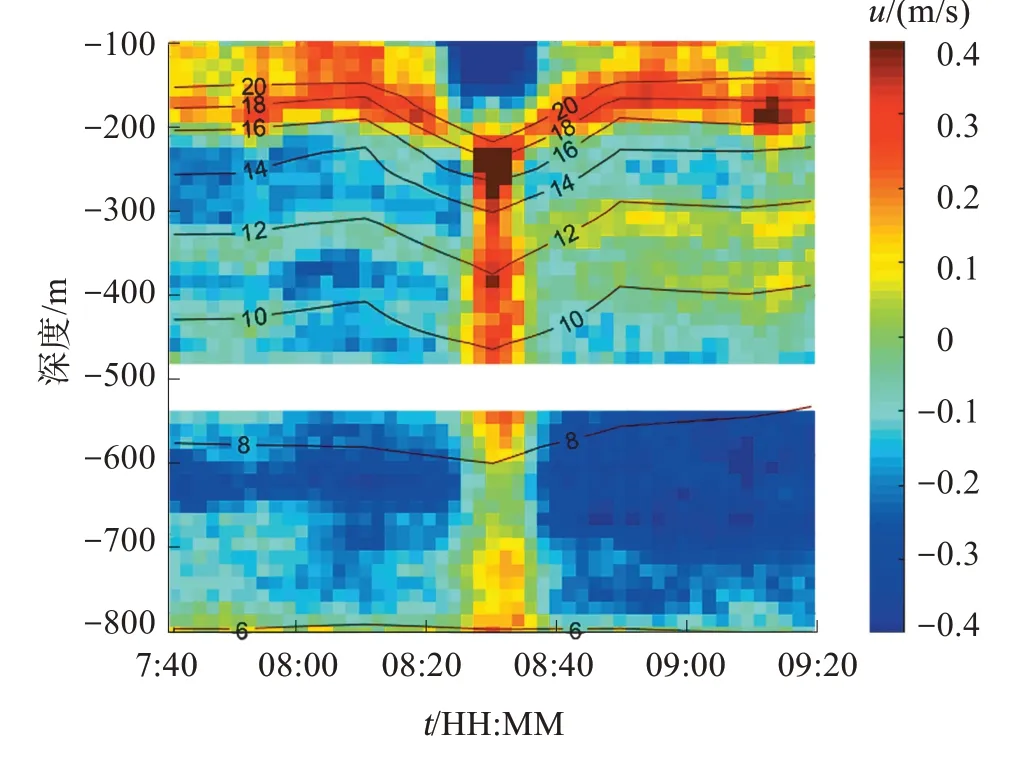
图5 2014年8月11日08：30观测到的内孤立波Fig.5 Internal solitary wave observed at 08:30 on August11,2014

4 结构物作用力时空演变特征

4.1 内孤立波模态分解

实际海洋中观测到的内波可以看成各个模态内波的线性叠加。考虑到该测站的实测海流数据的空间分辨率为16 m，有效数据位于78～478 m、553～825 m 水深，流速数据在垂直方向存在一定的缺少值，流速数据的空间分辨率相对较低。为了提高作用力计算的准确性，本文将观测到的内波视为多个模态内波线性叠加的结果，对实测海流数据进行内波动力模态分解，进一步推导出分辨率较高的流速数据。图 6给出了模态分解得到的归一化振幅W的垂直分布。图6 中，黑色实线代表第1 模态内波，虚色线代表第2模态内波，点线代表第3模态内波。通过前3 个模态的归一化振幅W，本文进一步计算了前3 个模态对应的流速（式(1)～(3)）。图7 是通过内波动力模态分解获得的东西方向水平流速对应的前3 个模态的时间-深度剖面，从图7 中可以很明显看出，第1模态流速方向在深度方向发生一次转向，上层向西传播，下层向东传播。此外，观测海区内波主要以前2个模态占主导，第1模态和第2模态东西方向的速度远远大于第3个模态东西方向速度。表明观测海区内波主要以前2 个模态占主导。因此，下文关于内孤立波对桩柱作用力计算中，主要关注前2个模态的作用力。

图6 前3个模态的归一化振幅W的垂直分布Fig.6 Vertical distribution of normalized amplitude W of the first three modes

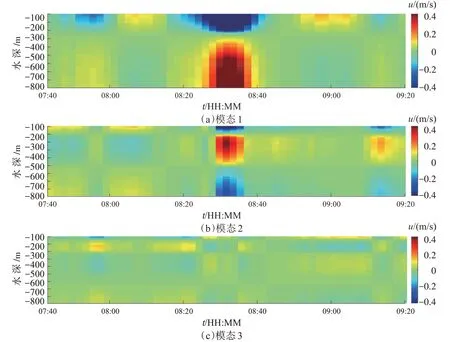
图7 3个模态东西方向流速垂向分布Fig.7 Vertical distribution diagram of east-west velocity of three modes

4.2 内孤立波对桩柱的总作用力计算

开发海洋资源常常需要将包括海洋平台等结构设备安置在海洋环境当中，当有海洋内波来袭时，内波与海洋结构之间的相互作用对结构物造成的影响是研究人员所关心的。考虑到海洋工程设备大多是由圆柱形构件组成的，本文对内孤立波与水平圆柱形桩柱的相互作用的问题进行了研究。

内孤立波经过时，会使周围的流场发生变化，内孤立波诱发的流场流速大，对结构物产生巨大的破坏作用［18］。在计算内孤立波对海洋结构物作用时，考虑到南海北部复杂背景环境的影响，ADCP 得到的实测流速可能会受到潮汐等背景流场的影响，本文将内孤立波到达前半小时和到达后半小时的流场看作背景流场，内孤立波所引起的波致流速等于实测流速减去背景流场的速度平均值。

对于小直径桩柱受力分析时，可以用Morison公式计算内孤立波的作用力，详见式(7)，其中CD和CM为经验系数，这2 个系数的取值与雷诺数、KC 数和表面的粗糙程度等因素有关［18］，需要由实验获得。依据前人在南海北部研究内波对海洋工程影响研究结果，本文选取CD和CM分别为0.6 和1.8［8,13］。取海水密度，桩柱直径D=5 m，得到的结果如图8。

图8 8月11日对应时间段各个模态作用力计算结果Fig.8 Calculation results of each modal force in the corre‐sponding time period on August 11

从图8计算结果中可以看到：

1）桩柱所受的总作用力都以第1 模态为主导，第2模态的作用力很小，相比较于第1模态基本可以忽略；

2）从时间上看，波谷达到时，对桩柱的作用力会达到最大值，并且作用力的大小呈现出先增大后减小的变化趋势。

4.3 内孤立波对桩柱作用力的垂向分布

为了进一步研究桩柱所受的作用力，对内孤立波的到达时，桩柱作用力沿水深方向的分布情况进行了研究。计算结果如图 9、10所示。

从图 9中可以得出，内孤立波波谷到达时，沿着水深方向作用力方向会发生变化，上层的总作用力为负值，在水平流速转向层附近会出现作用力方向的转变，下层的总作用力为正值，在作用力零点桩柱截面的作用力矩最大。从图 10 可以看出，第1 模态内孤立波对圆柱型桩柱的作用力大于第2模态内孤立波对圆柱型桩柱的作用力。此外，和图9 中总的作用力变化趋势相似，图10中，第1模态内孤立波对桩柱作用力在深度方向存在变化，上层的总作用力为负值，在水平流速转向层附近会出现作用力方向的转变，下层的作用力为正值。

图9 内孤立波波谷到达时桩柱作用力沿水深变化Fig.9 Variation of pile force along water depth when the inner solitary wave valley arrives

图10 各个模态的桩柱作用力垂向分布Fig.10 Vertical distribution diagram of pile force of each mode

4.4 作用力分量计算结果

本文对桩柱所受的2 个作用力分量，即拖曳力和惯性力分别进行了计算，计算结果如图11。从图11 中可以很明显看出，拖曳力项远远大于惯性力项。在内孤立波的传播过程中，计算得到的惯性力没有明显的变化趋势，但是惯性力对总作用力的贡献很小，相比于拖曳力，惯性力很小，对总作用力极值的影响也很小，基本可以忽略不计。

图11 8月11日对应时间段内作用力分量计算结果Fig.11 Calculation results of force components in the cor‐responding time period on August 11

为了进一步对比观测海区内孤立波对桩柱作用力中惯性力和拖曳力的演变，本文将采用简单的2层模型，以水平流速转向层为分界将海水分为上下2 层，计算内孤立波波谷到达时上、下层的惯性力、拖曳力和总作用力计算结果如表1所示。

表1 内孤立波对桩柱的上、下层拖曳力和惯性力的最大值Table 1 Maximum value of the drag force and inertia force of the upper and lower layers of the pile caused by the internal solitary wave

可以得到上、下2 层流体的拖曳力方向相反，惯性力的方向也是相反的，而在同一层流体中，拖曳力和惯性力的方向也是相反的。

5 结论

1）南海北部观测站位观测期间，内孤立波以前2 个模态占主导，内孤立波振幅可达80 m，内孤立波经过时，水平流速存在最大值，最大水平流速可达1 m/s。

2）桩柱所受的总作用力以第1 模态为主导；波谷达到时，对桩柱的作用力会达到最大值，并且作用力的大小都呈现出为先增大后减小的变化趋势。

3）上、下两层流体的拖曳力方向相反，惯性力的方向也相反，而在同一层流体中，拖曳力和惯性力的方向也相反。

4）在内孤立波经过时，Morison 方程计算得到的惯性力没有明显的变化趋势，惯性力相比于拖曳力，惯性力量值小，对总作用力的影响也很小，从工程的角度考虑，惯性力对总的作用力的影响基本可以忽略不计。