考虑扣件系统非线性力学行为的车辆与轨道动力分析模型

马登科，时瑾，王英杰

(北京交通大学 土木建筑工程学院，北京，100044)

铁路扣件是轨道上用以联结钢轨和轨下基础结构的关键部件[1]。扣件系统力学行为直接影响轮轨动力相互作用，扣件失效可能危及行车安全[2]。国内外学者在车辆与轨道动力学研究中往往将扣件系统简化为线性弹簧-阻尼单元[3-9]，但实际扣件系统主要由扣压件(扣件弹条)和支承件(轨下胶垫)组成，线性弹簧-阻尼模型难以模拟弹条松动或断裂造成扣压力损失情况，因此，非常必要开展扣件系统非线性力学行为的研究。

近年来，很多学者针对扣件系统非线性力学行为开展过相关研究，例如：OREGUI 等[10]建立不同类型的扣件模型，研究了扣件系统建模方式对单节轨枕轨道垂向动力学的影响；高亮等[11]分析扣件系统在不同受力阶段的垂向非线性刚度行为，提出了改进的抗拉刚度双线性模型和不受拉弹簧模型，表征扣压力失效的扣件，并分析了不同扣件失效类型对车辆-轨道系统动力响应特性的影响；王开云等[12]考虑扣件系统扣压件的预压力，建立了扣件垂向动力分析模型，分析了扣件垂向振动特性；袁玄成等[13]进一步建立了能够考虑钢轨扣件弹条扣压力和轨下胶垫初始压缩量的垂向动力学模型，分析了弹条扣压力衰减和扣压力失效对轮轨动力学响应的影响。上述研究建立了更为精细的扣件模型，但在反映扣件弹条和轨下胶垫在不同受力阶段的分段力学特征以及弹条与钢轨(绝缘块)间接触状态的时变特征方面存在不足，在模拟弹条力学特性及其失效方面与实际情况仍有一定的差异。

基于此，本文作者以高速铁路常用的W1型弹条扣件系统为例，建立精细的扣件系统有限元模型，揭示钢轨垂向运动时扣件弹条扣压状态和轨下胶垫支承状态的非线性力学特征；并进一步提出考虑扣件系统垂向非线性力学行为的车辆与轨道动力分析模型，开展扣件失效对轮轨系统动力学行为的影响研究，为扣件系统的损伤识别和养护维修提供一定的理论参考。

1 理论模型

1.1 扣件系统精细化有限元模型

基于有限元理论建立考虑弹条非线性接触关系的扣件系统精细化模型，如图1所示，具体建模过程和计算参数可参考文献[14-15]。需要注意的是，轨下橡胶垫板和铁垫板下弹性垫板作为扣件系统的弹性支承结构，在本文中统一表达为轨下胶垫。

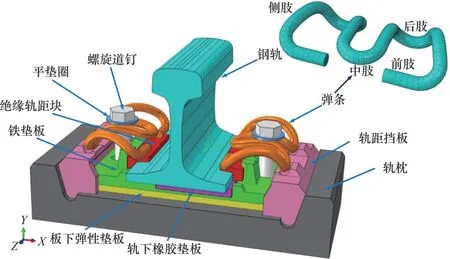
图1 扣件系统精细化有限元模型Fig. 1 Refined finite element model of fastening system

钢轨垂向运动时扣件系统力学行为是非线性变化的，如图2 所示，以向上运动为正方向(下同)。扣件弹条在紧固力矩作用下发生弹性变形(初始弹程Zrc0i)，对钢轨施加向下的扣压力；轨下胶垫则在扣压力作用下发生压缩变形(初始压缩量Zrp0i)，对钢轨产生向上的支反力，初始状态下二者保持平衡(钢轨相对于轨下结构的位移ΔZi=0)，此时扣件系统处于标准安装状态[16]，弹条中肢恰好与绝缘轨距块接触(本文近似考虑为与钢轨直接接触)。

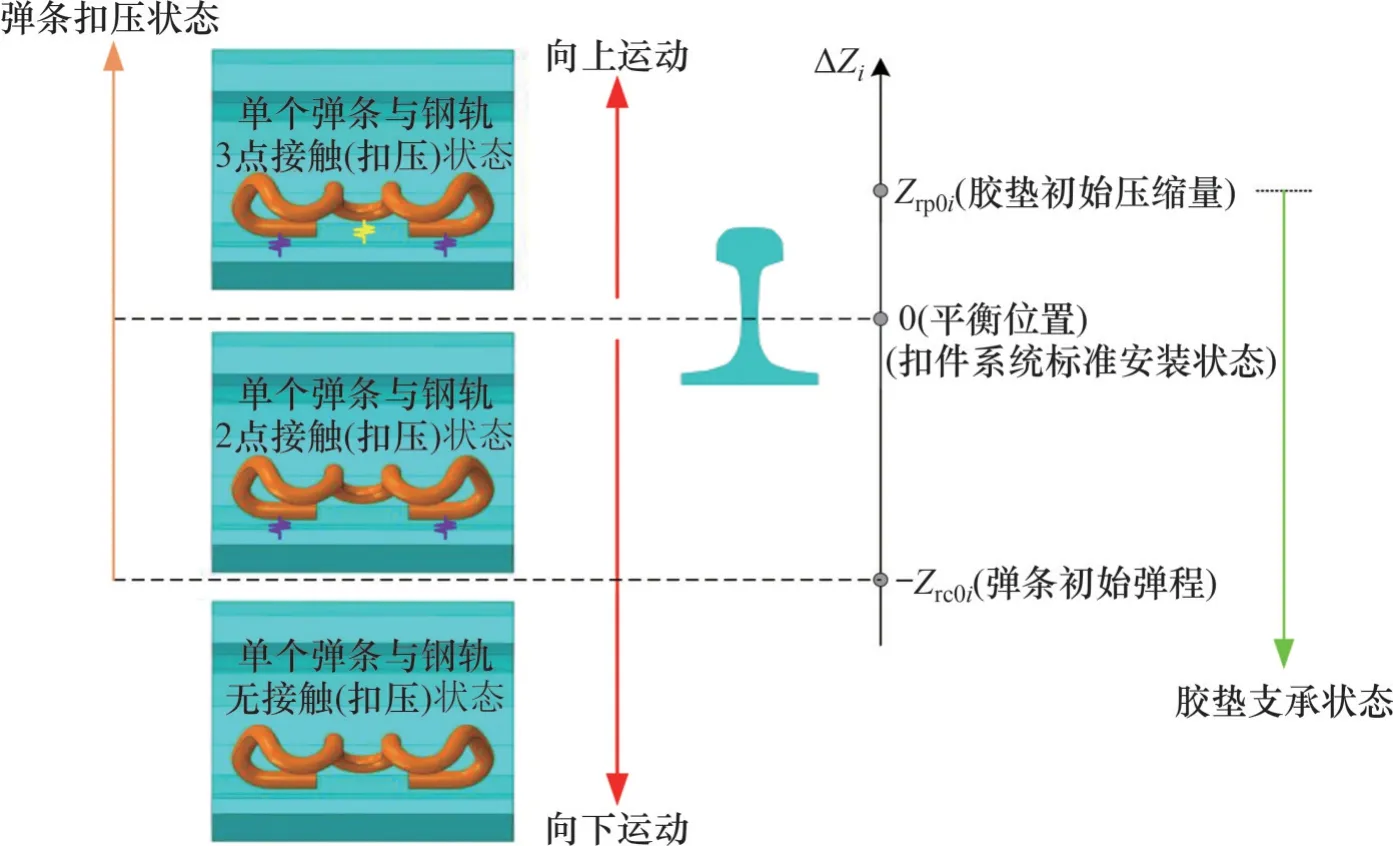
图2 钢轨垂向运动区间扣件系统非线性力学行为示意图Fig. 2 Diagram of nonlinear mechanical behavior of rail fastening system in vertical movement interval

当ΔZi≥0时，即钢轨相对于轨下结构向上运动时，弹条与钢轨处于“3 点接触”状态(即2 侧前肢+中肢)；

当-Zrc0i＜ΔZi＜0 时，弹条与钢轨处于“2 点接触”状态(即中肢无接触)；

当ΔZi≤-Zrc0i时，钢轨相对于轨下结构向下运动的位移大于等于弹条初始弹程，即弹条被彻底放松，对钢轨失去扣压作用，此时钢轨只受到轨下胶垫提供的支反力。

当ΔZi＜Zrp0i时，轨下胶垫发生压缩变形，对钢轨施加向上的支反力；

当ΔZi≥Zrp0i时，钢轨与轨下胶垫分离，轨下胶垫的变形恢复，其与钢轨之间失去相互作用力，此时钢轨只受到弹条施加的扣压力。

单个弹条的扣压力-弹程关系如图3 所示。由图3可知：弹条扣压力随弹程增大而近似呈双线性特征，分别对应“2 点接触”状态和“3 点接触”状态，临界点为标准安装状态，此时单个弹条的扣压力为9.477 kN，满足W1型弹条设计扣压力大于9.0 kN 的要求[16]。从“2 点接触”状态到“3 点接触”状态，单个弹条扣压刚度由0.675 kN/mm增大为5.110 kN/mm，即弹条单侧前肢的扣压刚度为0.337 5 kN/mm，中肢的扣压刚度为4.435 kN/mm。

图3 弹条扣压力-弹程曲线Fig. 3 Curve of clamping force-deflection

1.2 车辆与轨道动力分析模型

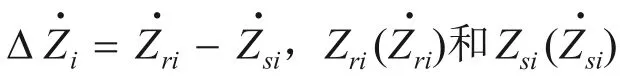
图4 改进的扣件系统精细模型Fig. 4 Improved refined model of fastening system

根据上述分析可知，随钢轨运动状态的改变，扣件弹条与钢轨之间的接触关系发生明显的变化，弹条对钢轨施加的扣压力也随之呈现分段特性，第i个扣件处的(两侧)弹条对钢轨施加的扣压力Fc-i为

式中：等式右边第一项表示第i个扣件处的弹条初始扣压力，对应的“4”表示两侧弹条共“4”个前肢；等式右边第二项和第四项分别表示钢轨运动引起两侧弹条“4”个前肢扣压力、阻尼力的改变量；等式右边第三项和第五项分别表示两侧弹条“2”个中肢扣压力、阻尼力的改变量。对应钢轨不同的运动状态，a0、a1(b1)、a2(b2)分别取值为0或者-1(弹条对钢轨施加向下的作用力)。

类似的，第i个扣件处的轨下胶垫对钢轨施加的支反力Fs-i为

式中：等式右边第一项表示第i个扣件处的胶垫初始压缩量引起的弹性支反力；等式右边第二项和第三项分别表示钢轨运动引起的胶垫弹性支反力、阻尼力的改变量。对应钢轨不同的运动状态，c0、c1(d1)分别取值为0 或1(-1)(轨下胶垫对钢轨施加向上的作用力)。值得注意的是，本文重点关注扣件弹条的力学特性及其失效对轮轨系统振动的影响，暂不考虑轨下胶垫的频(温)变特性。因此，本文动力模型计算时将轨下胶垫的垂向刚度和阻尼视为恒定值kr和cr。

综上，第i个扣件系统对钢轨施加的垂向作用力Fri即为该扣件位置两侧弹条扣压力和胶垫支反力的合力。结合图4所示的钢轨不同运动受力阶段扣件弹条、轨下胶垫的分段力学特征，且由于W1型弹条主要由60Si2Mn弹簧钢轧制而成[1]，其结构阻尼远比轨下胶垫的小，为简化建模，具体计算时可忽略弹条的阻尼(cti、cmi)。引入符号函数sign(x)，则Fri可进一步表达为

结合上述改进的扣件系统精细模型的具体表达关系，本文基于有限元理论[18]建立轨道系统垂向动力学模型。由于扣件弹条的振动是由钢轨引起的，且弹条的振动敏感频率相对较高，因此，在高频范围内获得准确的钢轨动态响应非常重要。众所周知，Timoshenko 梁模型在高频范围更加接近实际，因此，本研究钢轨采用Timoshenko 梁单元模拟；轨下胶垫采用离散弹性点支承进行模拟；轨道板参考高速铁路CRTS III 型板式无砟轨道[19]，将其简化为有阻尼弹性地基上的两端自由梁；同时，充分考虑高速铁路CRH3 车辆的车体、转向架、轮对、空气弹簧等物理结构特点[19]，运用多刚体动力学原理建立车辆系统垂向动力学模型；并采用Hertz 非线性弹性接触理论[20]计算轮轨间的垂向作用力，具体数值求解应用Newmark 法。本文建立的考虑扣件系统非线性力学行为的车辆与轨道动力分析模型如图5所示。

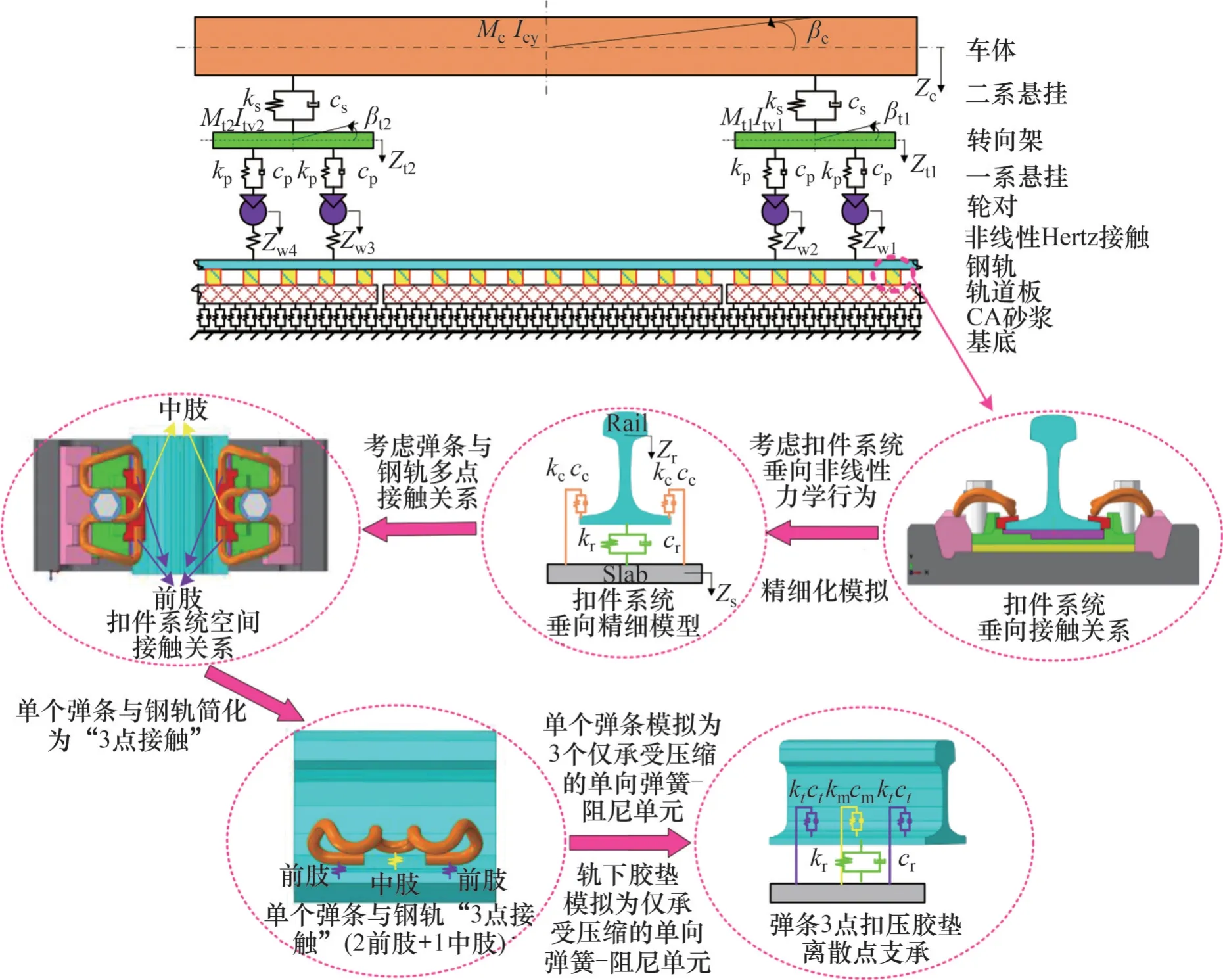
图5 考虑扣件系统非线性力学行为的车辆与轨道动力分析模型Fig. 5 Vehicle and track dynamic analysis model considering nonlinear mechanical behavior of fastening system

2 模型验证

2.1 本文模型的实测验证

为验证本文模型的可靠性，实测得到某高速铁路线路车辆300 km/h 运行经过时的钢轨垂向位移和垂向加速度响应。由于实测车辆为16节编组，为考虑多节编组的影响，同时提高计算效率，本文动力学模型计算时车辆考虑为2节编组，并输入测点附近的实测轨道高低不平顺，如图6所示。动力学计算参数参考文献[19]。

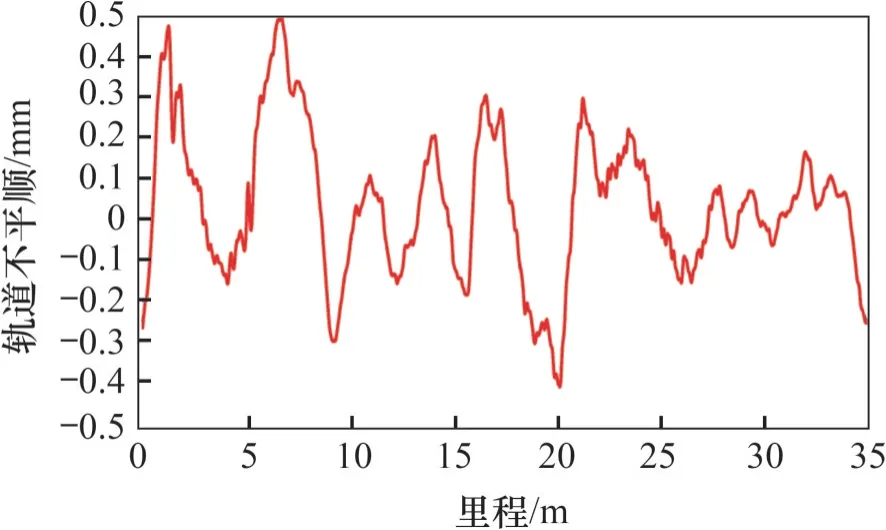
图6 实测高低不平顺Fig. 6 Measured track irregularity

现场实测与数值计算得到的钢轨动力响应(时程)结果如图7所示。由图7可知：实测和计算得到的钢轨垂向位移和垂向加速度较为吻合，验证了本文提出的车辆与轨道动力分析模型的计算可靠性。其中，取每辆车4个车轴经过时钢轨位移峰值的平均值，则计算结果与实测结果的最大相对误差为1.49%；取列车每个转向架经过时钢轨加速度峰值的平均值，则计算结果与实测结果的相对误差为1.26%，具体情况如表1所示。

表1 现场实测与数值计算的钢轨动力响应(峰值)对比Table 1 Comparison of dynamic response (peak value) between field measurement and numerical calculation

2.2 本文模型与传统模型对比

进一步以钢轨垂向位移和钢轨垂向加速度频谱作为对比指标，且不考虑轨道几何不平顺的影响，分析本文模型和传统车轨模型在钢轨振动响应和扣件系统相互作用力方面的差异性，结果如图8 所示。由图8 可以看到：2 种模型计算得到的钢轨垂向位移波形基本一致，但是在车轮靠近或者离开的时段，本文模型计算得到的钢轨位移振动幅值要比传统模型的大(如图8(a)中A 区域)，这是由于本文模型中弹条的扣压刚度远小于扣件系统的节点刚度，钢轨相对于轨下结构向上运动时受到的约束较小；而2种模型在钢轨垂向加速度频谱方面存在显著差异，特别是在100 Hz 以上区域，本文模型计算得到的频率100 Hz 以上的钢轨加速度响应较传统模型明显增大，与实际情况[13]更为接近，这表明本文模型在预测钢轨高频振动特性时更具备优越性。

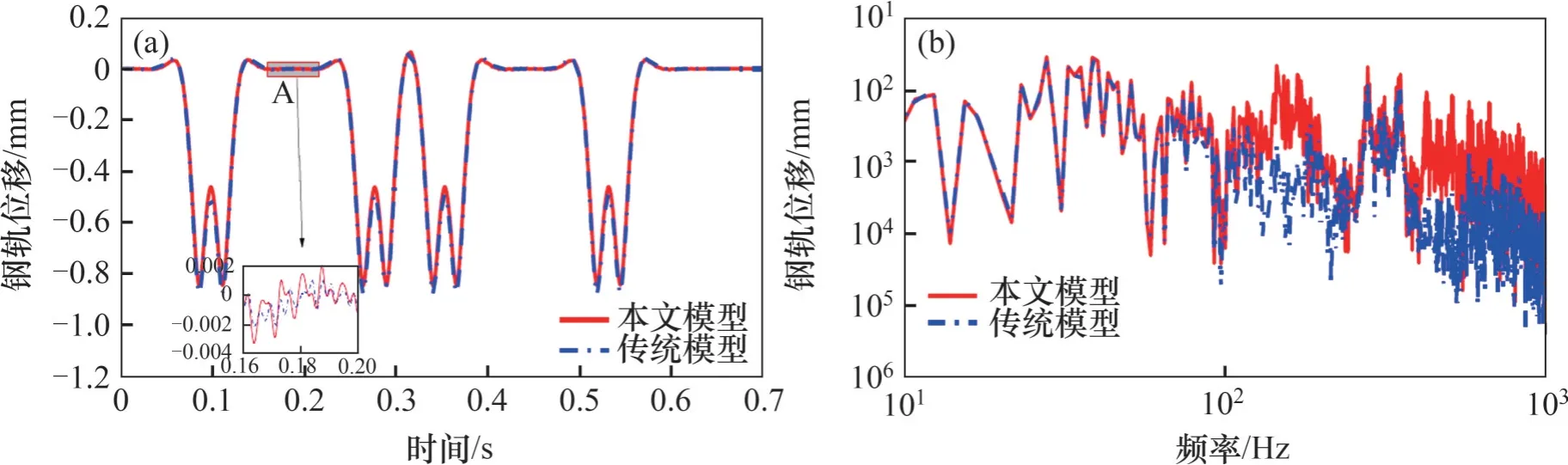
图8 本文模型与传统模型的钢轨动力响应对比Fig. 8 Comparison of rail dynamic response between proposed model and traditional model

图9所示为本文模型与传统模型计算得到的扣件系统对钢轨的垂向作用力对比。其中，本文模型考虑钢轨不同运动受力阶段扣件弹条的扣压力、轨下胶垫的支承力以及弹条与钢轨间的接触状态。因此，扣件系统对钢轨的垂向作用力可以细分为胶垫支反力和弹条扣压力；而传统模型由于将扣件简化为线性弹簧-阻尼单元，未细分扣件弹条和轨下胶垫的作用，扣件系统对钢轨的垂向作用力即等于胶垫支反力(无法计算弹条的扣压力)，负值表示钢轨受到弹簧-阻尼单元对其所施加向下的拉力作用(力的方向向上)。由图9 可以看到：2 种模型计算得到的扣件系统对钢轨垂向作用力的合力基本一致。但对于胶垫支反力，由于传统模型没有考虑弹条扣压力导致的胶垫预压缩量，因此传统模型的胶垫支反力初始值为0 kN；而本文模型考虑了弹条初始扣压力和胶垫的预压缩量，因此本文模型的胶垫支反力初始值为18.954 kN，对应的弹条扣压力为-18.954 kN；且由于轨下胶垫只承受钢轨的压缩作用，所以运动过程中胶垫对钢轨的支反力应该为大于等于0 kN。但是从图9中的局部放大图(C区域)可以看到，传统模型的胶垫支反力存在小于0 的情况，这是由于传统模型中的弹簧-阻尼单元没有细分胶垫和弹条的作用。

图9 扣件系统对钢轨的垂向作用力对比Fig. 9 Comparison of vertical force of fastening system on rail

3 工况研究

基于本文建立的动力学模型，进一步研究扣件弹条损伤失效对轮轨系统垂向动力学响应的影响。按弹条的失效形式和失效数量将研究工况设置为单个弹条失效(工况1)、1 对弹条螺栓松弛(工况2，扣压力衰减50%)、1对弹条失效(工况3)、连续3 对弹条失效(工况4)、连续5 对弹条失效(工况5)、连续7对弹条失效(工况6)、连续9对弹条失效(工况7)，同时为对比轨下胶垫失效与弹条失效的影响，增加设置1组胶垫和扣件弹条均失效的工况(工况8，类似于传统模型去掉弹簧单元)，如图10所示。计算失效区域和邻近失效区域(根据行车方向分为前、后邻近区域)的轮轨系统动学响应。其中，行车速度为350 km/h，且均不考虑轨道不平顺的影响。

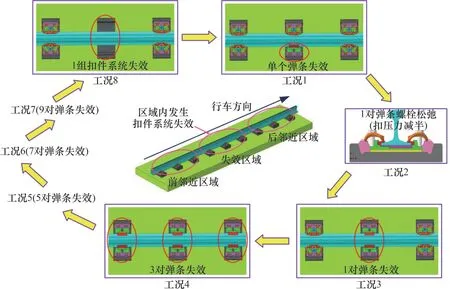
图10 扣件失效研究工况示意图Fig. 10 Schematic diagram of study conditions of fastening system failure

弹条失效区域轮轨动力学指标峰值计算结果如表2 所示。由表2 可以看到：相较于正常状态，失效区域内轮轨动力学指标均有一定程度的增加；工况8的动力学响应明显比其他工况的大，说明胶垫失效的影响显著大于弹条失效的影响。对比工况1～工况7 发现：工况4 和工况5 的动力响应较大，说明并不是弹条连续失效的数量越多，轮轨动力学指标就越大；工况2与正常状态的动力响应较为接近，说明1对弹条螺栓松弛对本文研究的动力学指标的影响可以忽略；工况1和工况2的胶垫支反力相较于正常状态小约9 kN，这是由于单个弹条失效和1对弹条螺栓松弛均造成失效位置处弹条的初始扣压力减半，即胶垫的初始支反力也减半；工况3～工况7的胶垫支反力相较于正常状态小约18 kN，这是由于弹条失效造成初始扣压力为0 kN，即胶垫无初始支反力；而工况8由于胶垫失效，因此失效位置处无胶垫支反力。

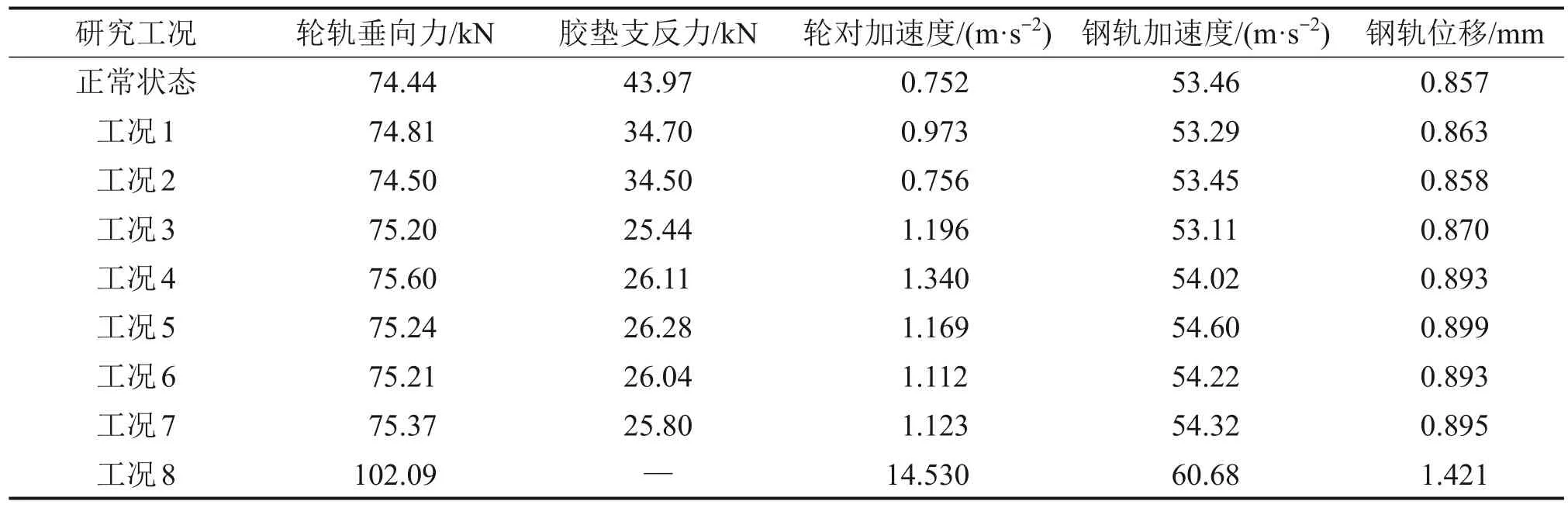
表2 弹条失效区域轮轨动力学指标峰值对比Table 2 Comparison of peak value of wheel-rail dynamics index in failure area of fastening clip

为进一步探究弹条失效对不同区域位置轮轨动力学指标的影响，以正常状态下的钢轨垂向位移峰值(向下)和上拱峰值作为基准，分别得到前邻近区域、失效区域和后邻近区域的动力响应变化量(相较于正常状态时的增大比例)，分别如图11所示。由图11 可以看到：对于钢轨垂向位移峰值，工况1～工况7失效区域和失效后侧邻近区域的响应较为接近，显著大于失效前侧邻近区域，且弹条连续失效5 对时的响应达到最大值，分别增加4.90%(失效位置)和4.65%(失效后侧)。对于钢轨上拱峰值，工况1～工况7 在失效区域处的响应均较大，且随着弹条连续失效数量增加而增大，工况7对应的增加量为10.30%。对于胶垫失效的情况，对比工况3 和工况8，可以看到胶垫失效时不同区域内轮轨动力学指标相较于弹条失效时显著增大，钢轨垂向位移峰值在失效后侧邻近区域达到最大值，即增加80.10%(对应弹条失效时为1.96%)；钢轨上拱峰值在失效区域达到最大值，即增加41.19%(对应弹条失效时为6.94%)。由此说明，传统模型利用刚度属性折减或去掉弹簧单元来实现扣件弹条失效的模拟，会放大失效区域附近的轮轨系统动力响应；且针对扣件失效的情况，包括弹条失效和胶垫失效，实际现场运营维护时不仅要关注失效区域内的轨道结构状态，对于后邻近区域也要及时加强关注。

4 结论

1) 本文模型全面考虑了钢轨不同运动受力阶段扣件弹条扣压力、轨下胶垫支承力的分段特征以及弹条与钢轨间接触状态的时变特征，能够更加准确地反映弹条和轨下胶垫的受力特性及其失效对轮轨系统振动的影响。

2) 随钢轨运动状态的改变，扣件弹条与钢轨之间的接触关系发生明显的变化，弹条扣压力随弹程的增大近似呈双线性特征，即单个弹条扣压刚度在“2点接触”状态时为0.675 kN/mm，在“3点接触”状态时为5.11 kN/mm。

3) 本文模型计算得到的频率100 Hz 以上的钢轨加速度响应较传统模型明显增大，与实际情况更为接近，即本文模型在预测钢轨高频振动特性时更具备优越性。

4) 相较于正常状态，扣件失效区域内轮轨动力学指标均有一定程度的增加；1对弹条螺栓松弛对轮轨系统振动的影响可以忽略，但其对应的弹条初始扣压力和胶垫初始支反力会减小；而胶垫失效的影响显著大于弹条失效的影响。

5) 对于钢轨垂向位移峰值，失效区域和失效后侧邻近区域的响应较为接近，显著大于失效前侧邻近区域，且弹条连续失效5对时的响应达到最大值，分别增加4.90%(失效位置)和4.65%(失效后侧)；对于钢轨上拱峰值，失效区域处的响应较大，且随着弹条连续失效数量增加而增大，最大增加量为10.30%。