基于边界约束刚度参数优化的轨道扣件弹条防断裂设计方法

邓士豪,王安斌,鞠龙华,杨 辉

(上海工程技术大学城市轨道交通学院,上海 201620)

引言

扣件弹条作为扣件系统的重要零部件，在运营过程中弹条损坏十分常见。弹条一旦发生失效，会使轮轨之间的相互作用更加剧烈，轨道稳定性及安全性下降，缩短轨道线路零部件的使用寿命，严重时引起列车脱轨，造成严重的安全事故[1-3]。针对扣件弹条断裂损伤问题，国内外学者从不同的角度采用不同的方法进行了研究。朱胜阳等[4]研究了弹条在安装过程中的受力及列车动荷载作用下的振动特性，并对比现场实测结果，发现钢轨波磨明显加剧弹条的振动，从而加速弹条疲劳损伤。赵才友等[5]对扣件弹条动力特性进行现场测试，用3种不同的方法对弹条的工作模态进行参数识别，提出改变螺栓扭矩从而改变弹条的工作模态，避免与轮轨系统激励共振。孟雷[6]从扣件扣压力性能方面对扣件系统服役性能进行了研究，提出应该健全扣压力检验标准，保证扣件技术性能。王开云等[7]利用轨道不平顺模型，分析扣件系统垂向振动特性，提出扣压件及垫层的弹性变形均受预扣压力及轮轨动态作用力的影响，扣压件及垫层作用在钢轨上的力均含有预扣压力及轮轨力的成分。文献[8-9]对弹条的断口宏、微观形貌、金相组织、硬度等进行分析，从弹条材料角度出发，认为弹条断裂是因组织缺陷造成的。高晓刚等[10]基于现场试验，通过弹条伤损区间钢轨动态位移的测试及钢轨波磨的检测和分析，认为扣件失效会加剧轮轨间相互作用。肖宏等[11]从时频角度分析验证e型扣件弹条断裂的本质原因，提出调整车辆运行速度来减少在扣件的损坏数量。陈明明等[12]基于扣件系统有限元模型进行安装状态受力特性分析，对弹条材料、工艺参数、表面处理等进行优化改进。综上所述，过去的研究主要集中于扣件系统的动力学特性、弹条受力变形以及材料组织缺陷等方面分析弹条断裂。

目前对于弹条在安装状态下、不同使用环境条件下模态辨识及理论分析缺乏深入的系统研究。基于此，以潘得路FC快速弹条为研究对象，对弹条在服役状态下的模态特征包括模态频率、模态振型等开展理论分析及试验研究，研究不同约束条件下的模态频率的变化规律，为弹条设计优化及安装条件提供理论依据，并指导线路的运营维护保养等。

1 弹条扣件系统分析模型

1.1 模态分析理论

弹条在列车高速通过轨道时，由于轮轨的滚动及冲击、轨道线路不平顺或钢轨波磨的激励作用，当弹条服役状态下模态频率与主要激励频率一致时，将引发共振响应，轮轨动态激励和轨道系统的振动特性决定了弹条对于各种动力荷载的响应大小和频率特征[13]。为从频域角度研究弹条断裂机理，选取模态分析作为弹条振动特性的研究方法，建立扣件弹条的运动方程为

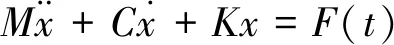
(1)

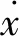
根据式(1)得到扣件系统的振动方程。在对弹条振动的频率和振型进行求解时，可以不用考虑阻尼的作用及影响，即可得到无阻尼强迫振动方程

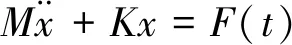
(2)

结构振动为简谐振动，即可假设位移为圆频率正弦函数

x=xsin(wt)

(3)

将式(3)代入式(2)得到相应的特征方程为

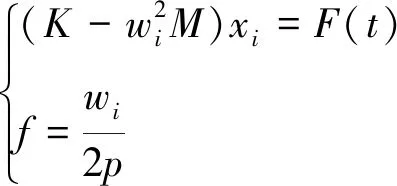
(4)

式中，ωi为弹条第i阶的模态固有频率，且i=1，2，3，…，n。f为自振频率，特征向量(xi)为固有频率ωi对应的特征向量，也是自振频率f对应的振型。

1.2 FC快速弹条模型建立

潘得路FC快速弹条扣件系统原型如图1所示，该扣件系统包含尼龙弹条帽、FC弹条、铁垫板、轨距挡块、橡胶垫板、垫圈和锚固螺栓8个零部件。为了便于后续对弹条进行理论和试验分析，将FC弹条各部位名称在图1中标出。

图1 FC快速弹条扣件系统

由图1可以看出，FC快速弹条形状复杂，体积小。弹条装配在铁垫板内，扣压在钢轨上，产生两个接触对：弹条与铁垫板接触对和尼龙弹条帽与钢轨接触对，边界条件和受力情况复杂[14]。采用整体扣件系统模型分析，计算时间长，收敛困难。因此，采用简化FC弹条模型进行分析。

为了比较真实地模拟弹条服役状态，对于FC快速弹条模型，约束弹条两后跟的垂向自由度，对于其横向和径向自由度，采用非线性接触理论处理弹条边界条件[15-17]，在弹条前扣压端底部、弹条两侧外趾上部和弹条两后跟下部单一网格节点上，设置多个方向的等效弹簧单元来模拟弹条与钢轨、弹条与铁垫板之间的接触关系，总体设置见图2、图3。其中弹簧单元设置为对地接触，可承受双向力即拉力和压力。通过设置不同的弹簧刚度，来模拟弹条与铁垫板接触对、弹条与钢轨接触对之间不同的摩擦阻力和工作状态。

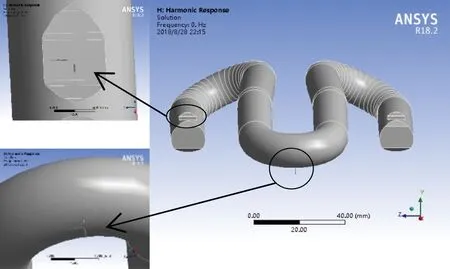
图2 弹条扣压端下部和左外趾上部弹簧单元

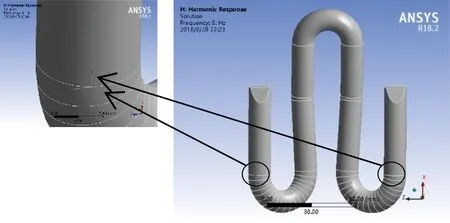
图3 弹条左、右两后跟下部弹簧单元

相比以往对弹条接触部位施加刚性约束，采用弹簧约束模拟零部件间相互的复杂受力状况，更接近实际工况。经过多次试算优化，最终确定弹条模型共划分29 639个六面体单元和104 645个节点。弹条有限元模型如图4所示。

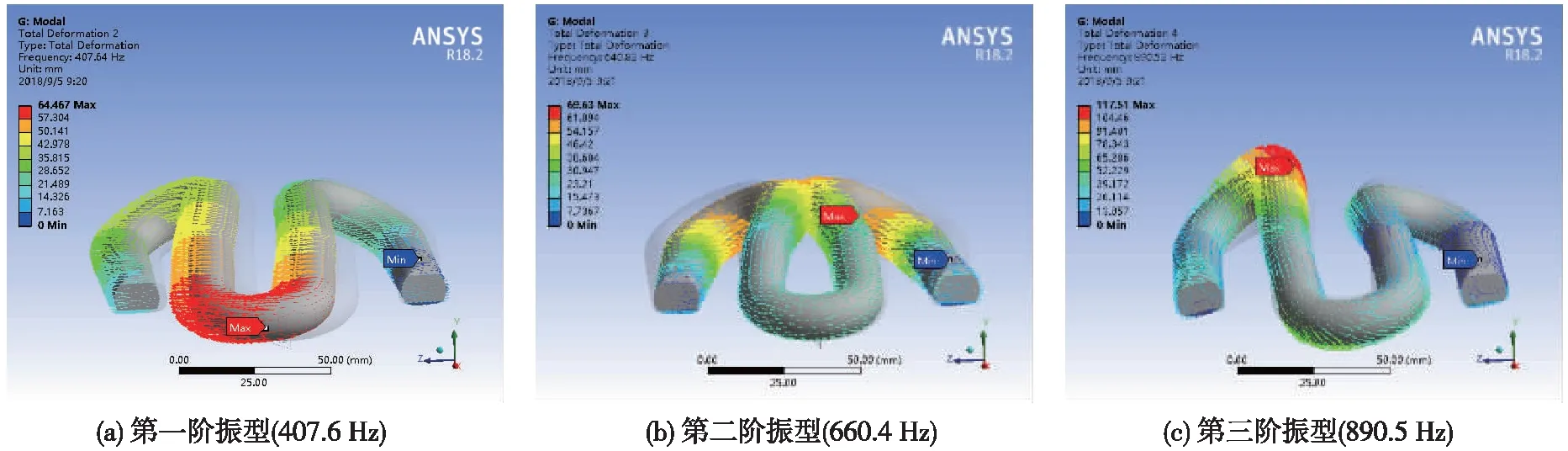
图5 FC快速弹条前三阶模态振型

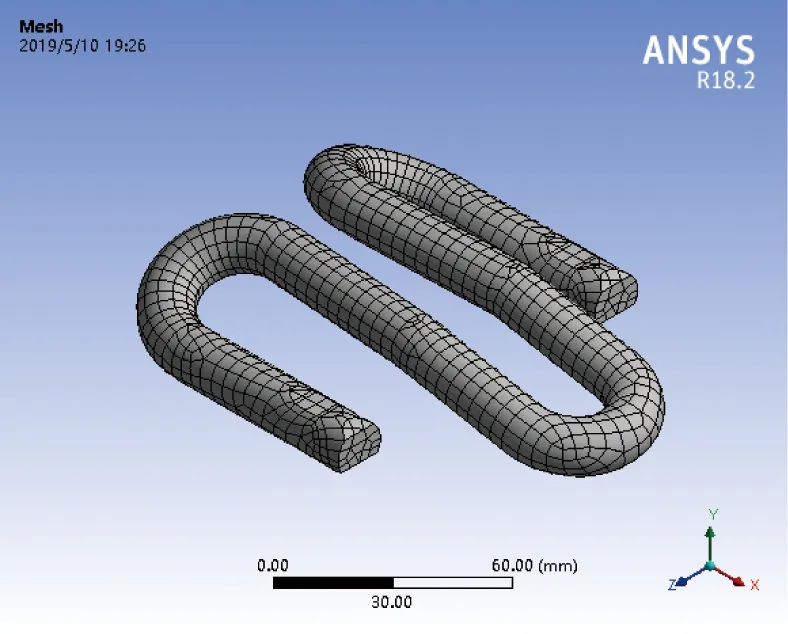
图4 FC快速弹条有限元模型

根据弹条材料的实际参数，确定所建立模型中的材料属性，如表1所示。弹条材料的应力-应变关系采用弹塑性模型。

表1 弹条材料参数

2 弹条服役状态模态验证与分析

为研究弹条在服役状态下的敏感频率以及振型变化情况，对其进行模态分析，参数和边界条件见第1节，以模拟弹条实际工作条件。以钢轨、道床、隧道壁主要参振频段为参考，以及钢轨波磨对弹条断裂的影响所涉及的波磨激振频率[18]，只考虑FC快速弹条在1 000 Hz范围内的模态频率，有限元分析结果如图5所示。

为验证FC弹条简化模型的正确性，便于进行下一步研究，将有限元仿真结果与弹条模态实测结果进行对比。

弹条模态测试采用多点激励，多点响应(MIMO)的方法，试验测试内容为弹条振动加速度[19]。弹条测点和加速度传感器布置示意如图6所示，数字表示敲击点，总共10个敲击点，左、右各布置1个加速度传感器，传感器测量弹条振动加速度。加速度传感器粘贴在弹条上，与弹条质量相比较，传感器对系统的附加质量对弹条动力特性影响很小，故可以忽略不计。因此，对传感器的选择主要考虑其量程、灵敏度、安装方便与否，采用了PCB-352C33型号压电加速度传感器，试验时设置采样频率为5 000 Hz，根据采样定理，分析有效频率范围为2 500 Hz，满足弹条分析考虑频率范围1 000 Hz要求。

图6 FC快速弹条测点和加速度传感器布置

力锤激励FC快速弹条激励点，对振动信号的采样进行加窗处理，并采用特征系统实现算法ERA模态分析法。在重点关注的1 000 Hz频率范围内，弹条的前三阶固有频率分别是400，660 Hz和901 Hz。对比结果如表2所示。

由表2可以看出，简化后FC弹条仿真结果与试验测试结果相差较小，误差在5%以内，验证了本文所建立的FC弹条简化模型的有效性，从而也验证了采用弹簧的单元来模拟边界约束刚度的合理性，为后续对快速弹条进行深入的研究奠定了基础，保证分析的准确性。

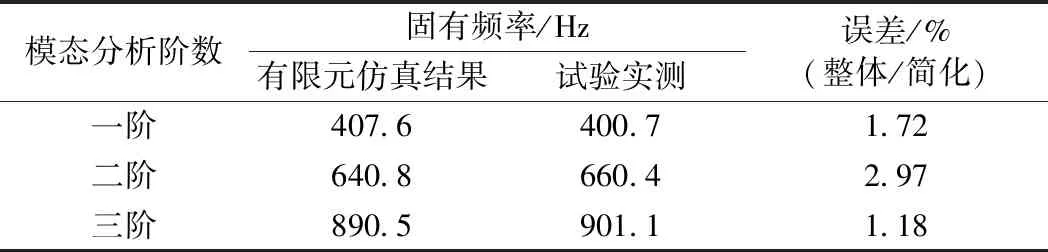
表2 本文有限元结果与实测结果对比

图5中，实体有箭头指示部分代表弹条变化振型，无颜色虚化部分代表弹条原始状态。由弹条前三阶模态振型可以看出，这些振型会造成弹条后拱受力复杂，具体振型描述见表3。

表3 弹条工作状态下前三阶固有频率及相应振型描述

由模态分析结果可以看出，弹条折断的本质原因是受到外界一定频率的激扰而引发共振。在该频率作用下，弹条各部位的应力幅值出现峰值，共振造成弹条振动幅度增大，特别是后拱拉压应力、扭转力增大(结合模态振型)，需要重点关注。在长期列车荷载作用下，弹条疲劳受损折断[20]。

3 不同约束刚度对弹条模态频率的影响

3.1 工况参数设置

在第1.2节中，对于弹条边界条件设置了不同方向，不同部位共计9个弹簧单元来模拟弹条与铁垫板、弹条与钢轨之间的接触关系，并通过设置不同的弹簧刚度值K，来模拟接触对之间的不同的摩擦阻力和工作状态。

为了定量分析9个弹簧单元不同的刚度值K对于弹条前三阶模态频率的影响，以第2节中取得的K值为中心，左右按相同梯度，各取3组数据:K1、K2、K3、K中心、K5、K6、K7，其中K中心表示该值为第2节中的刚度值，对不同的K值进行计算，共计63个工况。

3.2 模态分析结果与分析

3.2.1 弹条扣压端约束刚度对模态频率的影响分析

在弹条扣压端共设置了3个弹簧单元，分别是X、Y、Z三个方向(图2)。

对于X方向，取KX1=5 000 N/mm～KX7=17 000 N/mm，梯度为2 000 N/mm。并以此类推，分别对于Y方向，取KY1=150 N/mm～KY7=450 N/mm，梯度为50 N/mm；对于Z方向，取KZ1=300 N/mm～KZ7=600 N/mm，梯度为50 N/mm。

对单一方向取不同参数仿真计算时，均保持其余部位弹簧单元刚度值K保持不变。将以上3个方向的参数仿真计算结果汇总，如图7所示。

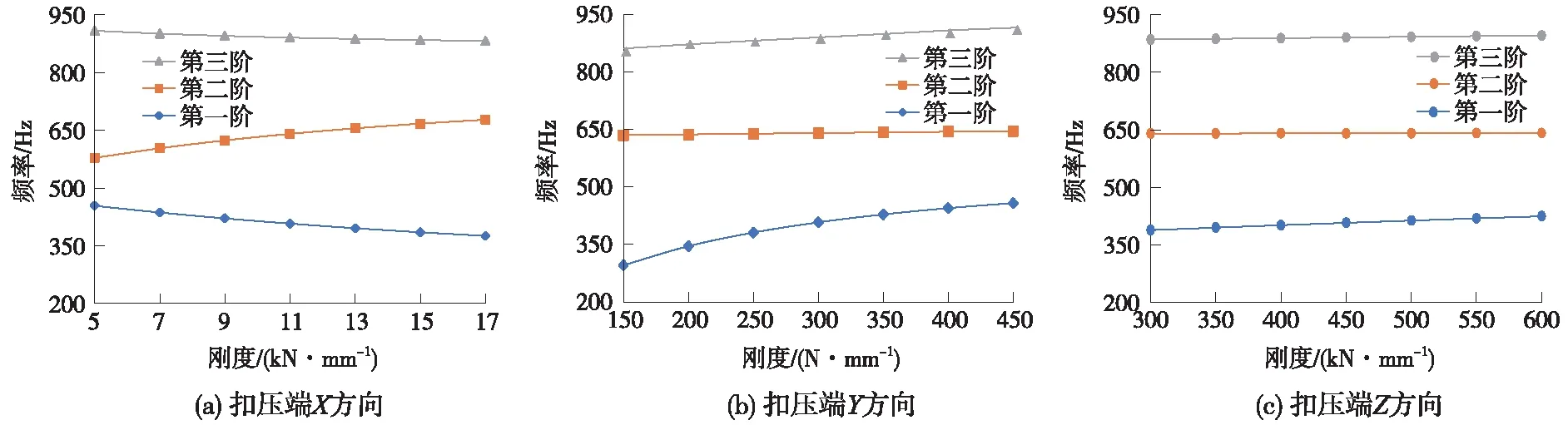
图7 弹条扣压端不同约束刚度下的模态频率计算结果

3.2.2 弹条两肢约束刚度对模态频率的影响分析

考虑到弹条成左右对称的结构特性，故只对弹条的一侧进行不同数值下的弹簧刚度的工况计算。在弹条左右趾上部各设置2个弹簧单元，两处均是X、Z两个方向，如图2、图3所示。

对弹条左外趾上部弹簧单元X方向，取KX上1=10 kN/mm～KX上7=40 kN/mm，梯度为5 kN/mm；对于Z方向，取值KZ上1=400 N/mm～KZ上7=1 600 N/mm，梯度为200 N/mm。将以上两个方向的参数仿真计算的结果汇总，如图8所示。

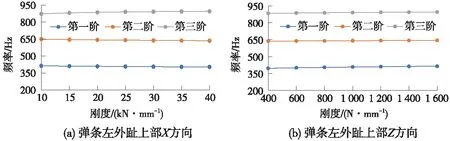
图8 弹条左外趾上部不同约束刚度下的模态频率计算结果

对弹条左后跟下部弹簧单元X方向，取值KX下1～KX下5=30 kN/mm梯度为5 kN/mm； 对于Z方向，取值KZ下1=400 N/mm～KZ下7=1 600 N/mm，梯度为200 N/mm。将以上两个方向的参数仿真计算的结果汇总，如图9所示。

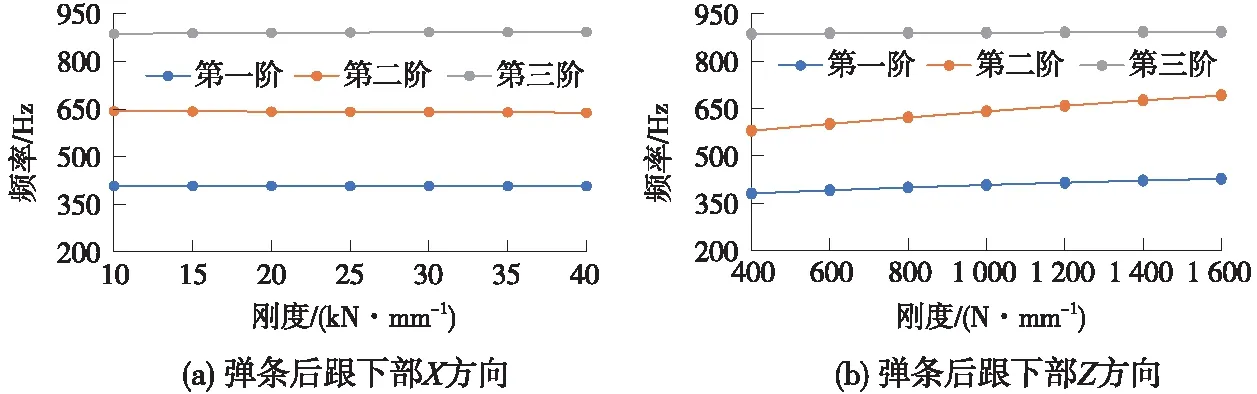
图9 弹条后跟下部不同约束刚度下的模态频率计算结果

将以上分析结果进行汇总，得出弹条不同部位不同方向约束刚度对弹条前三阶模态频率的灵敏度系数(Δf/Δk)，如表4所示，其中正值代表正相关关系，负值代表负相关关系。

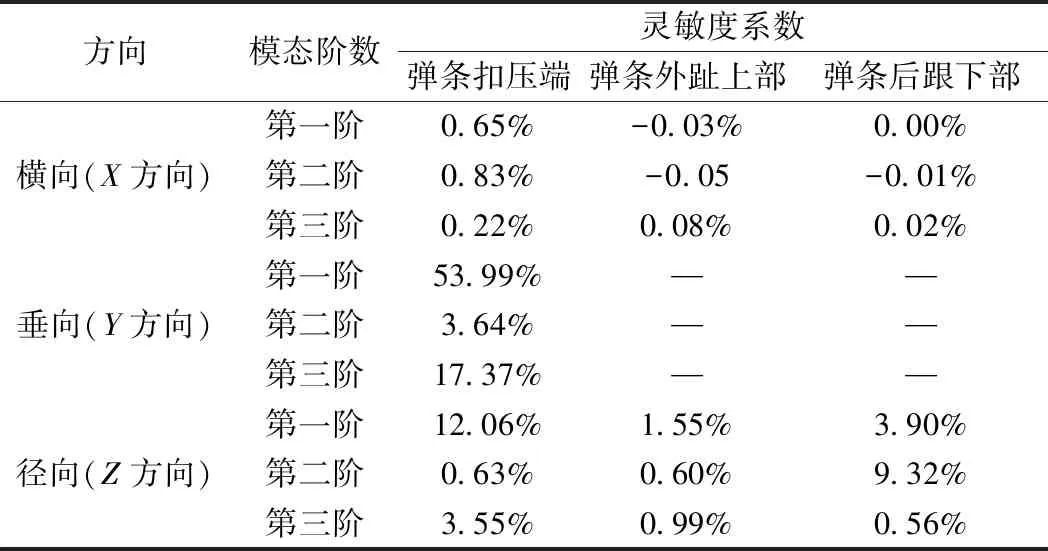
表4 弹条不同部位约束刚度对模态频率灵敏度

从图7～图9的约束刚度取值可以发现，弹条扣压端约束刚度要小于弹条外趾约束刚度。从图1可以看出，弹条扣压在钢轨上，扣压端套有尼龙弹条帽，而弹条左、右两外趾则被铁垫板紧固。因此，弹条扣压端与钢轨间的摩擦系数要小于弹条左、右两外趾与铁垫板间的摩擦系数，故弹条扣压端约束刚度小于弹条外趾约束刚度，符合实际情况。

由表4可以看出，弹条扣压端约束刚度以及弹条后跟下部对弹条前三阶模态频率有较大的影响，而弹条两外趾约束刚度则对其影响相对较小。进一步观察可以发现，弹条扣压端Y方向(即垂向)约束刚度对弹条第一、第三阶模态频率有显著影响，两者呈现正相关关系；弹条后跟下部的Z方向(即径向)约束刚度的上升，则会引起弹条第二阶模态频率的显著增加。

根据文献[20]的研究成果，钢轨波磨对弹条振动有很大影响，不同线路上钢轨波磨的波长和幅值有所不同，同一线路不同地段的也存在差异。弹条折断的主要外因是服役状态下模态频率与波磨激振频率一致引发共振[21]。因此在安装过程中，需要根据实际的线路条件，选择合适的安装位置以及合适的扣压力，通过改变弹条服役状态，调整其模态频率，避免与列车高速通过时的激振力激励弹条的频率一致，从而避免共振，防止弹条断裂。

3.3 不同约束刚度下弹条谐响应分析

列车运行过程中，钢轨承受来自于车轮的垂向和横向荷载作用，为了进一步分析弹条的振动幅值特性，按钢轨垂向荷载、钢轨横向荷载两种工况对弹条进行研究，从频率响应角度分析弹条易断裂区域的应力。

在弹条频响分析中简谐作用力为1 kN，选取2处区域作为简谐荷载作用点，作用点1在弹条扣压端下部，模拟钢轨垂向荷载；作用点2在弹条扣压端前部，模拟钢轨横向荷载，如图10所示。根据第2节模态分析得出的弹条模态振型，重点关注弹条断裂位置(即后跟靠近两端内侧位置，以下简称后跟内侧)，设置2个响应点，如图11所示。

根据第3.2节，弹条各部位在不同约束刚度下对模态频率的影响分析结果，重点研究弹条前部扣压端Y方向(即垂向)以及后跟下部Z方向(即径向)约束刚度与弹条频响的关系。

对弹条分别施加1 kN垂向、横向简谐荷载，弹条前部扣压端不同垂向刚度下的弹条频响曲线如图12所示；弹条后跟下部不同径向刚度下的弹条频响曲线如图13所示。

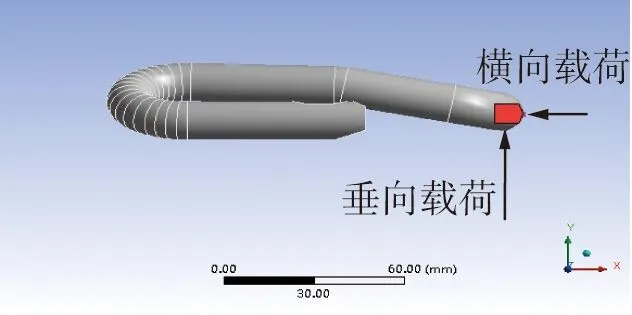
图10 垂、横向荷载作用点

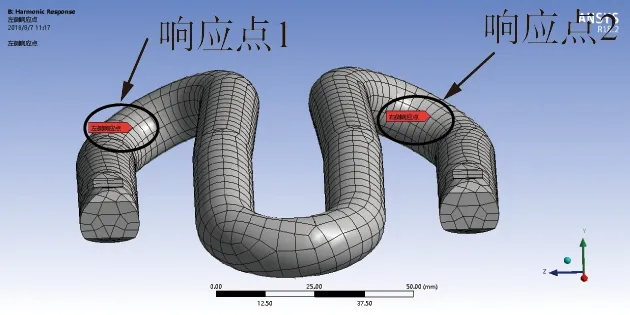
图11 左侧、右侧响应点

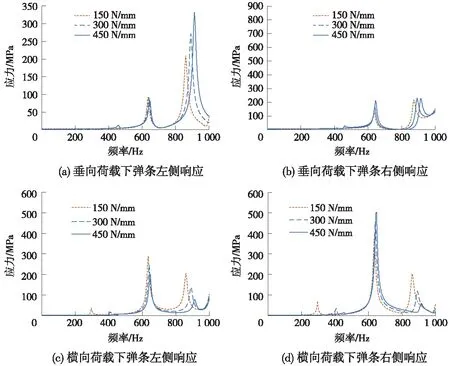
图12 不同垂向刚度下弹条频响曲线

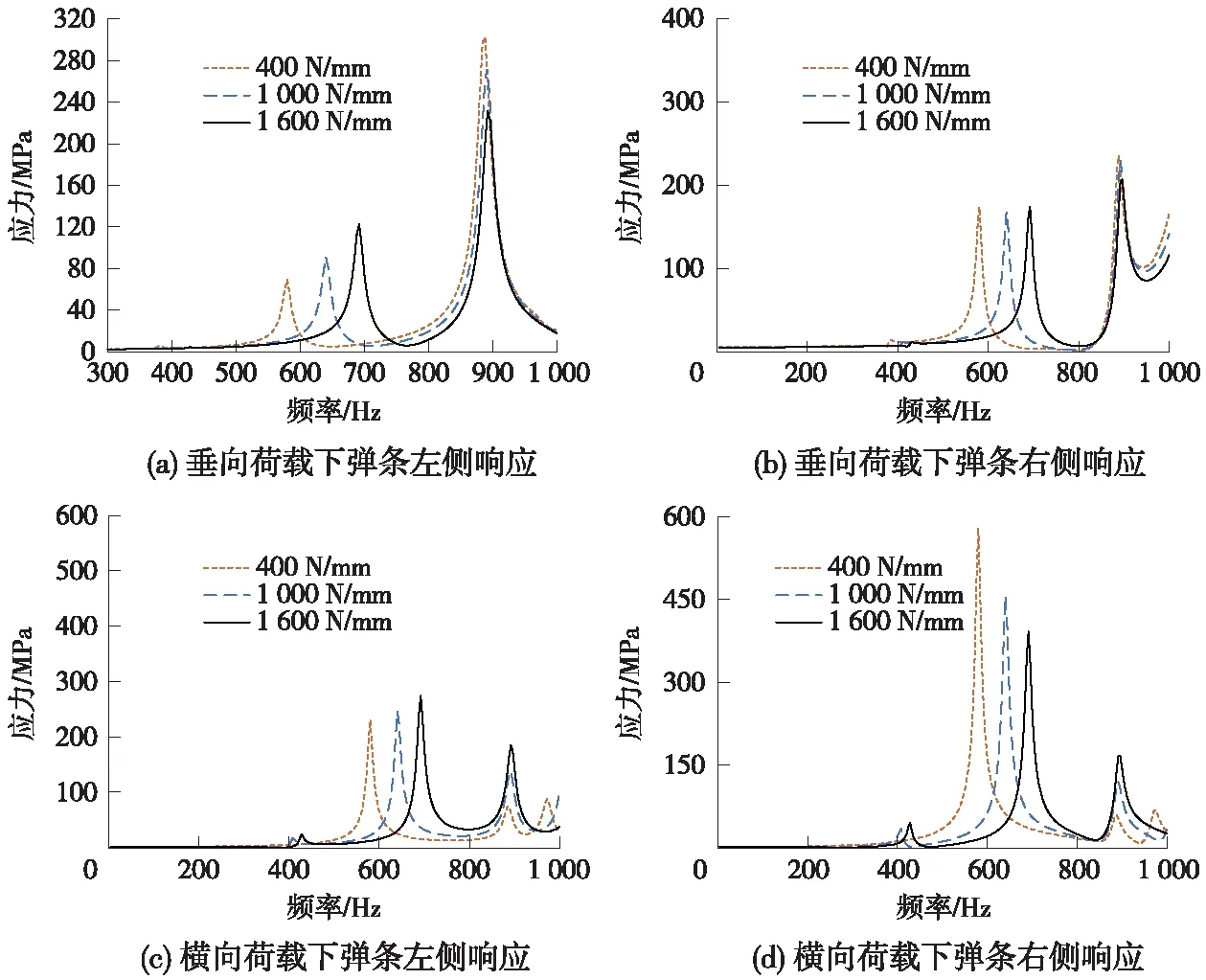
图13 不同径向刚度下弹条频响曲线

结合图12、图13可以看出，在垂向、横向谐振荷载作用下，弹条的左侧、右侧响应点均出现了1个在400 Hz左右的微弱峰值，以及2个明显的峰值，且幅值较大，分别在660 Hz左右和900 Hz左右，说明在钢轨载荷激励作用下，弹条的后两阶模态频率响应较大。结合模态分析结果，得出共振峰所在频率与第2节弹条模态分析所得到的前三阶固有频率保持一致。值得注意的是，弹条第一阶共振频率的幅值远小于第二、第三阶共振频率幅值，由此说明第二、第三阶模态频率为危险频率，防断裂设计时应重点考虑。结合模态振型可以看出，在弹条服役状态下，这两阶频率会使得弹条后跟会受到较大的拉压应力和弯曲应力等复杂应力，在长期循环荷载作用下，会造成折断病害。

4 结论

为了避免扣件弹条在服役过程中因共振发生断裂，通过实验室试验并建立FC快速弹条有限元模型，分析不同边界条件下弹条模态频率的变化，并基于数值结果，得出以下结论。

(1)通过在弹条前扣压端底部、弹条两端外趾上部和弹条两端后跟下部设置多个方向弹簧单元来模拟弹条与铁垫板、弹条与钢轨之间的接触关系，建立与试验结果相一致的有限元模型，以代替分析整套扣件系统实体模型，提高计算效率，同时保证计算收敛和准确性。

(2)通过对FC快速弹条的不同部位施加不同的约束刚度进行模态分析发现，弹条前部扣压端的垂向约束刚度对弹条前三阶模态频率有显著影响。其中，弹条第一阶(400 Hz)、第三阶(900 Hz)模态频率与弹条前部扣压端垂向刚度(150～450 N/mm)呈明显的正相关关系；弹条后跟下部的径向约束刚度(400～1 600 N/mm)对弹条第二阶频率(660 Hz)有正相关作用。

(3)以模态分析结果为依据，对FC快速弹条进行谐响应分析发现，在不同约束刚度边界条件下，弹条服役状态的共振频率有较大差异，弹条的共振峰的幅值变化也有明显的区别。弹条第一阶共振频率的幅值远小于第二、第三阶共振频率幅值，由此说明第二、第三阶模态频率为危险频率，防断裂设计时应重点考虑。

(4)结合试验结果和有限元仿真结果可知，如果在弹条设计和安装中结合其相应的模态频率、振型。根据实际线路约束条件，对弹条予以针对性设计，可避免与列车激振频率一致引发共振。由于扣件弹条的工作模态与其边界条件是紧密相关的，因此，对于不同的轨道结构形式，如有砟轨道和无砟轨道，以及不同的铺设基础，如桥梁、路基或隧道内，其配套的弹条扣件的安装状态等需考虑的技术参数尚需进一步测试研究。