高速铁路环境振动黏弹性边界数值模型及验证
张志俊
(贵州理工学院土木工程学院,贵阳 550003)
为确保线路平顺性、减小线路工后不均匀沉降,我国高铁线路多采用“以桥代路”的方式修建。高速列车在桥上运行时的振动能量通过桥墩传递到周围自由场及临近建筑物中,由此产生二次振动和噪声,对铁路沿线的环境产生诸多不利影响,激起国内外学者的研究兴趣[1]。
桥上列车运行引起的地面振动受到诸多因素影响,例如:车辆、轨道和桥梁的动力特性;轮轨非线性接触;轮轨不平顺;线桥相互作用关系;基础动力阻抗;土体耗能特性等[2]。振动波由桥梁基础传递至自由场,其本质上是波在以土体为介质的半无限域中的散射问题[3]。采用有限元等数值方法[4]求解该问题时,需引入虚拟的人工边界从半无限介质中截取出有限尺寸的计算域,以消除模型边界处波的反射与透射。人工边界一般可分为全局人工边界和局部人工边界[5]。局部人工边界由于其所具有的时空解耦特性和计算耗时少等特性,在有限元方法中得到广泛应用。黏弹性人工边界属局部人工边界,其能够模拟人工边界外半无限介质弹性恢复性能,避免了黏性边界带来的低频漂移问题,具有良好的频率稳定性[6]。
在车致环境振动的数值模拟研究方面,陈建国、夏禾等[7]建立了车-桥和墩-土两个子系统模型,分析了诸多因素的影响规律,并采用回归方法提出了相应预测公式。曹艳梅等[8]采用半解析/有限元模型对高速列车通过连续梁桥引起的环境振动进行了预测。朱志辉等[9]建立了考虑土-结构相互作用的车-桥-墩-桩-土耦合振动系统整体三维有限元分析模型,对京沪高铁沿线软土地基的振动响应进行研究。Connolly等[10]采用有限元-无限元相结合的数值模型模拟地基土,研究了高速铁路路基段的车致环境振动问题。李小珍等[11]采用数值方法研究了弹性支座对车致环境振动问题的减振特性。冉汶民等[12]通过求解频域动态轮轨力,将其施加于站房结构有限元模型进行求解。高广运等[13]采用有限元法对高铁桩网符合路基环境振动的影响因素进行分析。卢华喜等[14]建立了列车作用下路基-凸起地形的二维有限元计算模型,研究凸起地形对铁路环境振动的影响。
本文将黏弹性人工边界应用于自由场中波传播衰减过程的数值模拟。由于问题的复杂性,涉及影响因素较多,需首先采用车-线-桥耦合振动理论[15-16],以轨道不平顺为激励,考虑轮轨相互作用,通过数值积分求解车-线-桥系统动力响应;再以此为激励,通过大型通用有限元软件ANSYS建立墩-桩-土黏弹性边界有限元模型,模拟波在自由场的传播衰减过程。最后,通过现场试验测试结果,对数值分析结果进行验证,从而判断该方法的适宜性。
1 数值模型
1.1 数值模拟过程解析
列车过桥引起的环境振动问题涉及车辆、轨道、桥梁、基础及其周围场地等诸多系统,具体求解过程见图1。模型分为两个子系统,车-线-桥耦合振动子系统及墩-桩-土子系统,两个子系统由桥梁支座反力进行联系。由车-线-桥耦合振动子系统求解出桥梁支座反力,将其施加到墩-桩-土子系统的桥墩顶部作为激励,求解其引起的桥墩周围自由场振动响应。

图1 车致环境振动分析过程
1.2 车-线-桥子系统耦合振动理论
车-线-桥耦合振动分析模型是由车辆、轨道、桥梁模型按一定轮、轨运动关系和线、桥相互作用关系进行联系的系统。运用车辆动力学、轨道动力学和桥梁动力学理论,将车辆、轨道和桥梁看作一个耦合动力体系,分别建立车辆、轨道和桥梁运动方程,以轮/轨关系、线/桥关系为纽带,运用数值仿真方法求解车-线-桥系统动力响应。其车辆子系统、轨道子系统、桥梁子系统3部分的运动方程分别为

(1)

(2)

(3)

以上动力学方程相关理论推导、数值仿真及试验验证等详见文献[15,17],此处不再赘述。
1.3 墩-桩-土子系统数值模型
1.3.1 黏弹性人工边界
本文引入时域黏弹性人工边界从半无限介质土体中截取出有限尺寸的近场计算域。具体地,在边界上添加切向和法向弹簧-阻尼单元进行模拟[18]。如图2所示,图中坐标X、Y沿人工边界的切向,Z为法向,图中黏弹性人工边界节点上物理元件的参数为

(4)
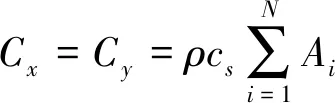
(5)

(6)

(7)


图2 三维黏弹性人工边界示意[18]
该人工边界的精度,可通过与Lamb问题理论解析解[19]对比得出。考察Lamb表面激振问题:针对匀质、各向同性半空间,其自由表面施加F的集中垂向荷载作用(图3)。模型水平方向尺寸为0.5 m,垂向尺寸为1 m,实体单元尺寸均为0.1 m。材料的剪切模量取16,密度取1,泊松比为0.25。荷载表达式为

(8)

(9)
式中,T为加荷时间;H(τ)为Heaviside阶梯函数。
如图3所示,截取Lamb问题的1/4模型进行对比分析,荷载施加于O点,输出A点的位移响应,紧邻O点的两个立面为轴对称面,施加轴对称边界,模型底面及另两个立面均为人工边界。将固定人工边界、黏弹性人工边界及解析解的结果进行对比,如图4所示。从图4可以看出,相对于固定边界,黏弹性人工边界结果更接近于解析解,幅值及波形与解析解吻合度更好。

图3 Lamb问题有限元模型

图4 不同边界数值分析与解析解结果对比
1.3.2 墩-桩-土有限元模型
建立墩-桩-土三维有限元模型,如图5所示。
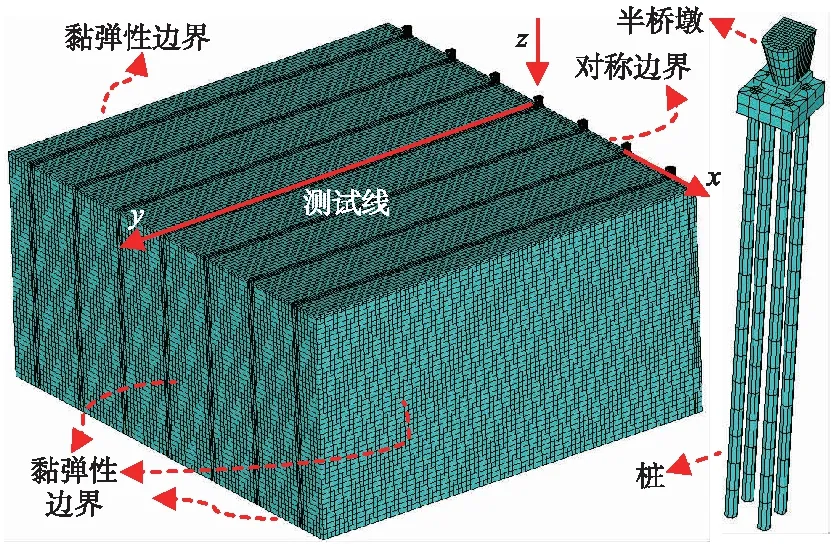
图5 墩-桩-土3D有限元模型
如图5所示,由于z方向激励引起沿y方向分布的响应关于x轴轴对称分布,为减少模型单元数,节约计算时间,引入轴对称边界,则仅建立一半模型(模型中仅包含一半桥墩、一半桩基及一半场地土),另一半模型用轴对称边界代替,墩顶支座反力激励仅施加一半。模型底部及另三个立面均采用前文所述三维时域黏弹性人工边界进行处理,土体参数如表1所示,与文献[20]中试验场地的土层参数一致。有限元模型长245 m、宽225 m、深112 m,桥墩范围(即振源处)单元尺寸为0.5 m,单元最大尺寸为2.5 m,基本满足有限元分析对单元的尺寸要求[21]。该模型共包含524 216个3D实体单元,43 146个弹簧-阻尼单元和35个两节点的3D梁单元。

表1 模型土体参数
2 数值分析及验证
2.1 模型参数
本次计算所用模型参数均来源于津秦客专一跨度32 m桥梁段环境振动现场测试工况,详见文献[20]。测试车辆为CRH380A型高速列车,8节车辆编组,轴重约140 kN。轨道不平顺采用德国低干扰谱。桥梁全长32.6 m,计算跨径31.5 m,设计活载ZK标准活载,设计车速350 km/h,线间距5 m,梁体典型截面如图6所示。桥墩墩高3 m,桩基采用钻孔灌注桩,桩长37 m,桥墩及基础尺寸如图7所示。桥上采用CRTS-Ⅱ型板式无砟轨道,二期恒载140 kN/m。

图6 箱梁横截面(单位:cm)

图7 桥墩与基础示意(单位:cm)
2.2 数值分析结果验证
以车速为350 km/h工况下的数值分析结果与实测结果进行对比。
图8给出了车速350 km/h时,根据车-线-桥耦合振动理论,通过数值积分求得的桥梁支座反力时程。列车为8节车辆编组,可清晰从支反力时程曲线中分辨出首尾处半节车辆的影响及中间显著的7节车辆引起的支反力峰值。

图8 支座反力时程(V=350 km/h)
将图8所示支座反力的一半施加于图5所示模型的桥墩墩顶,通过有限元软件求解出支座反力激励引起的自由场动力响应。为了与文献[20]中现场测试结果进行对比,数值分析响应输出的位置与文献[20]现场测点一致,如图9所示。

图9 响应输出位置(单位:m)[20]
图10给出了测点1处的加速度时程数值分析与文献[20]中现场试验结果的对比曲线。由图10可以看出,计算结果与试验结果时程曲线波形和幅值吻合度均较好。
图11给出了车速为350 km/h时,测点1和测点5两测点处数值分析与现场测试结果[20]的加速度1/3倍频程谱对比曲线。
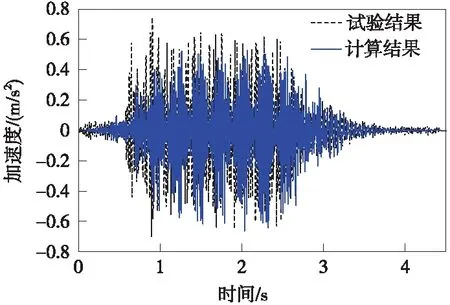
图10 测点1处的加速度时程(V=350 km/h)

图11 加速度1/3倍频程谱对比(V=350 km/h)
由图11可以看出,地面两个测点的振动峰值频率均为50 Hz,测点1在80 Hz频率处响应存在第二峰值,测点5处的响应则在高于峰值频率的频段迅速衰减,导致在80 Hz频率点的第二峰值频段不再显著。从两个测点的数值分析与5次实测结果的对比可知,在20 Hz以下频段,数值计算结果比测试结果稍大;在优势频段(31.5~65 Hz),数值分析结果与测试结果吻合较好;在较高频段(63~100 Hz),测点1处的数值分析结果比测试结果稍大,而测点5处的数值分析结果比测试结果稍小,可以看出数值分析结果在高频段的振动响应随距离衰减的速度比实测结果更快。
图12给出车速350 km/h时,各测点数值分析结果与5次实测结果的总振级对比。由图12可以看出,无论是数值分析还是现场测试结果,总振级随与桥梁距离增加而逐渐增大,可以看出振动波在自由场传播过程中不断衰减。5次测试结果与数值分析结果在每个测点处的具体数值均存在一定差值,但可看出其差值较小,且振动衰减的趋势基本趋于一致。

图12 各测点总振级对比
3 结语
建立合理有效、简单易行且具有足够精度的数值分析模型对于复杂的列车运行引起自由场振动问题具有重要意义。将此问题所涉及的多因素复杂系统分为车-线-桥子系统和墩-桩-土子系统,两个子系统之间通过支座反力进行联系。对于波在半无限介质土体传播过程中涉及的人工边界问题,采用了三维时域黏弹性人工边界。通过求解Lamb问题的数值算例与理论解析解对比可知,黏弹性人工边界更接近于解析解,计算精度较高。将该边界条件用于车致环境振动问题进行研究时,由于系统更为复杂,影响因素也更多,采用现场试验结果与数值分析结果进行对比。数值建模时,为减小模型单元数,提高计算效率,合理引入对称边界,建立半模型。
针对响应结果,从时域和频域内分别进行对比。从时域分析结果看,试验及数值模拟的时程曲线波形和幅值吻合均较好。从1/3倍频程谱对比可以看出,试验及数值模拟的响应峰值均为50 Hz左右,优势频段为31.5~65 Hz。由各测点的总振级随距离增加的衰减趋势可以看出,响应随与振源距离的增加而衰减。经数值分析与试验结果对比,各次试验结果并非完全一致,数值分析结果与试验结果之间也存在一定差值,但差值均较小,吻合度较好。

