WJ-8型小阻力扣件轨下橡胶垫板滑出动力学研究

李　晶

(青海交通职业技术学院,西宁　810003)



WJ-8型小阻力扣件轨下橡胶垫板滑出动力学研究

李晶

(青海交通职业技术学院,西宁810003)

摘要：基于轨下胶垫滑出后扣件支撑刚度减小和轮轨系统动力学基本原理,建立车辆-轨道-桥梁垂向耦合动力学模型,计算分析轨下胶垫滑出对车辆与轨道结构的动力学性能的影响,得出以下结论：(1)随着轨下胶垫滑出量的增加,车辆与轨道结构的振动加速度、钢轨与道床板的垂向位移、最大轮轨力、减载率均有增大趋势；最小轮轨力有减小趋势；且随着轨下胶垫滑出量的增加,车辆以及轨道结构的动力学指标的变化趋势逐渐增大。(2)基于车辆以及轨道结构的动力学指标,轨下胶垫滑出量不宜大于120 mm。

关键词：WJ-8型小阻力扣件；轨下胶垫滑出；轮轨系统动力学原理；动力学指标

WJ-8型小阻力扣件广泛应用于我国大跨度桥上无砟轨道无缝线路，其在减小梁轨相互作用的同时，也出现了梁端轨下胶垫滑出、轨下胶垫拉坏等问题。在温度变化、列车荷载循环作用下，大跨桥梁端梁轨相对位移过大，轨下胶垫在钢轨的往复运动中，逐渐滑出。恶劣环境下的轨底锈蚀造成轨下胶垫与钢轨摩擦阻力增大，也会使轨下胶垫滑出[1-4]。

轨下胶垫滑出，梁轨相互作用减小，梁端梁轨相对位移增大，将导致轨下胶垫进一步滑出。轨下胶垫滑出，轨下支撑刚度减小，将会影响轨道结构的稳定性以及行车的安全性。张凌之[5]通过试验测试了WJ-8型小阻力扣件的纵向阻力，郭成满[1]通过试验测试了轨下胶垫滑出对扣件纵向阻力的影响，将针对大跨桥上轨下胶垫滑出后，扣件的垂向刚度减小，并基于轮轨系统动力学原理，通过Ansys/lsdyna建模计算，对轨道结构以及行车安全性的影响进行动力学研究。

1计算模型与参数

1.1　力学模型

如图1所示，建立车辆-轨道-桥梁垂向耦合动力学模型，模型中将车体、转向架和轮对均考虑为刚体，忽略其弹性变形，只考虑各刚体沿垂向的振动，并且考虑两股钢轨上的垂向不平顺相近。因而，车体、构架各有浮沉、点头2个自由度，假设振动过程中车轮不脱离轨面运行，车轮的位移与轨面垂向不平顺相等，则车轮没有振动自由度，整个车辆系统一共6个自由度，即采用全车平面模型。桥跨的布置如图2所示，桥跨总长度约546 m；轨道结构采用叠合梁模型，钢轨采用离散弹性点支承基础上Euler梁模拟，支承点间隔为扣件间距，即0.65 m，扣件考虑为弹簧-阻尼单元；道床板采用单元板，用梁单元模拟；桥梁采用梁单元模拟，其中支座分为固定支座与活动支座；道床板与底座间的支撑考虑为弹簧-阻尼单元；梁端处梁轨相对位移较大，计算时考虑梁端5组扣件轨下胶垫滑出。

图1　车辆-轨道-桥梁垂向耦合振动全车平面模型

图2　桥跨布置(单位：m)

1.2　计算理论分析

假设轨面不平顺的时程函数为ηr(t)，则4个车轮下的轨面不平顺激励分别为ηri(t)，(i=1、2、3、4)，利用哈尔顿原理[6-12]建立振动方程。

系统的总动能

式中mc、Jcξ——单侧车体的参振质量和点头转动惯量；

mb、Jbξ——单侧转向架构架的参振质量和点头转动惯量；

zc、ξc——车体的沉浮和点头振动位移；

zbi、ξbi——前后构架的沉浮和点头振动位移。

系统的总势能

式中k1、k2——一系、二系悬挂的垂向刚度；

l1——转向架上前后两轮对一系悬挂点的纵向中心距之一半；

l2——车辆的二系悬挂点的纵向中心距之一半。

系统的总虚功

式中c1、c2——一系、二系悬挂的阻尼。

1.3　主要参数及评价指标

车辆采用CRH2型车，钢轨采用CHN60钢轨，轨道结构采用桥上单元双块式无砟轨道结构，扣件采用WJ-8型小阻力扣件，其主要参数如表1所示。

表1　计算主要参数

轨下胶垫滑出后，扣件的动刚度减小。轨下胶垫刚度计算经验公式[13]如下

kc=∂EA/H

式中∂——外形系数相关函数；

E——胶垫弹模；

A——胶垫支撑面积；

H——胶垫厚度。

轨下胶垫滑出后，胶垫支撑面积减小。由公式计算可知，动刚度取值与胶垫滑出量的关系如表2所示。

表2　WJ-8型小阻力扣件的动刚度取值

长波不平顺是影响行车舒适性的主要原因，为研究轨下胶垫滑出对行车的影响[2]，选用长波不平顺作为轨道激励。图3表示采用自编程序生成的德国低干扰谱高低不平顺样本。

由于轨下胶垫滑出主要影响车辆和轨道系统的垂向振动，因此主要考虑轮轨系统垂向动力特性的评价指标。根据相关资料文献，轮重动态减载率安全值取为0.6；车体垂向振动加速度的舒适性标准取为0.13g；最大轮轨垂向力允许值为170 kN；钢轨下沉量合理范围为1.5～2.0 mm[9]。

图3　德国低干扰谱高低不平顺样本

2计算结果与分析

列车速度取为350 km/h，考虑梁端5组轨下胶垫滑出，不同轨下胶垫滑出量时，车辆轨道系统动力学指标极值计算结果如图4～图7所示。

图4　轨下胶垫滑出量对车辆动力学性能的影响

图5　轨下胶垫滑出量对钢轨动力学性能的影响

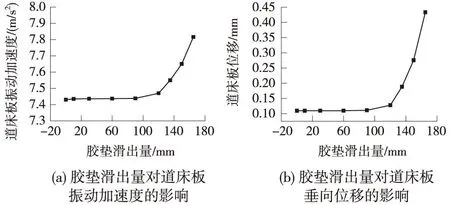
图6　轨下胶垫滑出量对道床板动力学性能的影响

图7　轨下胶垫滑出量对橡胶垫板应力的影响

2.1　轨下胶垫滑出对车体影响

轨下胶垫滑出后，轨下支撑刚度变小，当车辆行至轨下胶垫滑出区域，车体的加速度、轮轨力以及减载率均会发生变化，从而影响行车的舒适性以及安全性，图4表示轨下胶垫滑出量对车体动力学性能的影响。

由图4可知，当轨下胶垫滑出量较小时，胶垫滑出量对车体的加速度、轮轨力以及减载率影响均较小，主要原因是周边扣件对钢轨起到一定的协调支撑作用。但当胶垫滑出量达到90 mm时，其车体的加速度出现增大的趋势，并且随着胶垫滑出量的增加，其增大趋势逐渐增大，车体加速度的最大值为0.74 m/s2，小于其允许值0.13g。当轨下胶垫滑出量达120 mm时，最大轮轨力开始增大，增大趋势随着胶垫滑出量的增加而增大，当胶垫滑出量达165 mm时，其增幅达12.8%，仍小于其允许值170 kN；当轨下胶垫滑出量达120 mm时，最小轮轨力开始减小，减小趋势随着胶垫滑出量的增加而增大，当胶垫滑出量达165 mm时，减幅达64.5%。当轨下胶垫滑出量达120 mm时，减载率开始增大，增大趋势随着胶垫滑出量的增加而增大，当轨下胶垫滑出量为150 mm时，减载率为0.64，大于其允许值0.6，故胶垫滑出量须小于150 mm。

2.2　轨下胶垫滑出对钢轨的影响

轨下胶垫滑出，胶垫对钢轨的支撑作用较小，当车辆行至胶垫滑出区域时，钢轨的振动加速度、垂向位移均会发生变化，图5表示轨下胶垫滑出对钢轨的动力学性能的影响。

由图5(a)可知，随着轨下胶垫滑出量的增加，钢轨振动加速度也随之增大，且增大趋势随着胶垫滑出量的增加而增大，即胶垫滑出量越大，其对钢轨振动加速度的影响越大。由图5(b)可知，随着轨下胶垫滑出量的增加，钢轨垂向位移也随之增加，且增大趋势随着胶垫滑出量的增加而增大；当胶垫滑出量为120 mm时，钢轨的垂向位移达1.98 mm，接近钢轨垂向位移的允许值的最大值2 mm，故胶垫滑出量不宜大于120 mm，当轨下胶垫滑出量为165 mm时，钢轨的垂向位移达5.35 mm，远超钢轨垂向位移的允许值的最大值2 mm。钢轨的振动加速度增大，将加速钢轨表面不平顺的形成，甚至加速钢轨的磨耗，进一步影响行车舒适性和钢轨寿命；钢轨垂向位移增大，除影响车体的平稳运行和钢轨本身的受力外，还将影响下部结构正常运行。

2.3　轨下胶垫滑出对道床板的影响

轨下胶垫滑出，其支撑刚度减小，将影响轨道结构的传力过程，进而影响双块式无砟轨道道床板的受力特性。当车辆行至胶垫滑出区域时，道床板的振动加速度、垂向位移均会发生变化，图6表示轨下胶垫滑出对道床板的动力学性能的影响。

由图6(a)可知，当轨下胶垫滑出量较小时，胶垫滑出对道床板振动加速度影响较小，原因是轨下胶垫滑出量较小时，其影响没能从扣件传至道床板结构，但当轨下胶垫滑出量达90 mm时，道床板振动加速度开始增大，且增大趋势随着胶垫滑出量的增加而增大。由图6(b)可知，当轨下胶垫滑出量较小时，胶垫滑出对道床板垂向位移影响较小，但是当轨下胶垫滑出量达90 mm时，道床板的垂向位移开始增大，且增大趋势随着胶垫滑出量的增加而增大，当轨下胶垫滑出量为165 mm时，较之正常情况下其增幅达303%。综上可知，轨下胶垫滑出量较大时，轨下胶垫滑出对道床板的动力学性能影响较大，故实际运营过程中，应对梁端扣件进行实时监控，谨防扣件的轨下胶垫滑出量过大。

2.4　轨下胶垫滑出对扣件的影响

轨下胶垫滑出后，橡胶垫板的支撑面积减小，将会影响橡胶垫板自身的受力特性。当车辆行至胶垫滑出区域时，橡胶垫板的应力会发生变化，图7表示轨下胶垫滑出对道床板的动力学性能的影响。

由图7可知，轨下胶垫滑出量较小时，胶垫滑出对橡胶垫板应力的影响较小，当胶垫滑出量达90 mm时，橡胶垫板应力开始增大，且增大趋势随着胶垫滑出量的增加而增大，当胶垫滑出量达165 mm时，橡胶垫板应力为14.74 MPa，较之正常情况下增幅达300%。橡胶垫板的压应力过大，将影响橡胶垫板的性能，长此以往橡胶垫板容易被压坏，从而影响扣件系统的正常使用。

3结论与建议

针对轨下胶垫滑出，扣件支撑刚度减小，基于轮轨系统动力学原理，建立车辆-轨道-桥梁垂向耦合动力学模型，得出以下结论。

(1)随着轨下胶垫滑出量的增加，车辆与轨道结构的振动加速度、钢轨与道床板的垂向位移、最大轮轨力、减载率均有增大趋势；最小轮轨力有减小趋势；随着轨下胶垫滑出量的增加，车辆以及轨道结构的动力学指标的变化趋势逐渐增大。

(2)基于车辆以及轨道结构的动力学指标，轨下胶垫滑出量不宜大于120 mm。

(3)运营过程中，应对梁端扣件系统进行实时监控，谨防轨下胶垫滑出量过大，并对胶垫滑出的扣件及时进行维修。

参考文献：

[1]郭成满，杨荣山.WJ-8型小阻力扣件轨下胶垫滑出纵向阻力试验研究[J].铁道科学与工程学报，2015(4):4-8.

[2]张重王，刘学毅.不平顺谱对列车轨道系统动力性能影响的对比分析[J].铁道标准设计，2015，59(7)：15-20.

[3]苏立平，魏娟.基础刚度突变对双块式无砟轨道振动的影响[J].兰州工业学院学报，2014，21(5):46-49.

[4]李莉，王书卫.钢轨扣件减振橡胶动态刚度特性分析[J].同济大学学报，2013(2):21-25.

[5]张陵之.小阻力扣件纵向阻力特性研究[D].成都：西南交通大学，2014.

[6]蔡小培，高亮.采用新型钢轨焊缝保护装置后钢轨焊缝处的轮轨动力学特性[J].中国铁道科学，2012，33(3):49-54.

[7]翟婉明，涂贵军，高建敏.地铁线路钢轨焊接区轮轨动力学问题[J].振动、测试与诊断，2012，32(5):702-708.

[8]杨荣山，刘克飞，任娟娟，等.砂浆伤损对轮轨系统动力特性的影响研究[J].铁道学报，2014，36(7):79-84.

[9]刘学毅，王平.车辆-轨道-路基系统动力学[M].成都：西南交通大学出版社，2010.

[10]刘克飞.框架型板式轨道水泥乳化沥青砂浆伤损及维修标准研究[D].成都：西南交通大学，2013.

[11]刘克飞，刘学毅.橡胶浮置板轨道垂向动力特性分析[J].铁道建筑，2012(8)：113-115.

[12]李成辉.振动理论[M].成都：西南交通大学出版社，2014.

[13]王其昌.无砟轨道钢轨扣件[M].成都：西南交通大学出版社，2006.

Dynamic Research on the Sliding of Rubber Pads of WJ-8 Small Resistance FastenersLI Jing

(Qinghai Vocational and Technical College, Xi’ning 810003, China)

Abstract：Based on the decreasing of supporting stiffness on account of the sliding of pads and the basic principle of the wheel-rail system dynamics, the vehicle-track-bridge vertical coupling dynamic model is established to calculate and analyze the dynamic performance of the vehicle and the track structure subject to the sliding of pads. The results show that: (1)with the increasing of the sliding of the pads, the vibration acceleration of the vehicle and the track structure, the vertical displacement of the rail and road slab, the maximum wheel-rail force, reduction rate of wheel load are all increasing; and the minimum wheel-rail force decreases; and with the increasing of the sliding of the pads, the change of dynamics indicators of the vehicle and the track structure tends to increase; (2)based on dynamic parameters of the vehicle and the track structure, the sliding of the pads should not be more than 120 mm.

Key words：WJ-8 small resistance fasteners; Sliding of pad; Dynamic principle of wheel-rail system; Dynamic parameters

中图分类号：U213.5+3

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.02.011

文章编号：1004-2954(2016)02-0053-04

作者简介：李晶(1983—)，女，讲师，E-mail:2952547471@qq.com。

收稿日期：2015-06-24； 修回日期：2015-07-05