基于虚功原理的轨下支承失效动力响应研究

杨宏印, 吴楠昊, 曹鸿猷, 张 威, 刘章军

(1. 武汉工程大学 土木工程与建筑学院,湖北 武汉 430073;2.桥梁结构健康与安全国家重点实验室, 湖北 武汉 430034; 3. 武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)

0 引 言

列车高速通过桥梁时产生的振动会激发轨道振动,轨道通过轨道垫层将振动传递给桥梁(路基),同时由于车辆激励引发桥梁(路基)和轨道的振动亦会反作用于车辆系统,进而影响列车走行的稳定性和安全性。这种相互作用就是列车与轨道和桥梁(路基)之间的耦合振动问题。道床板在长期列车荷载和温度荷载下容易发生混凝土破碎、在自然条件下逐渐风化和粉化。道床板脱空或者扣件支承失效会造成轨下丧失支承接触面,导致轨枕发生松动的现象。车-轨-桥耦合作用会在轨下支承失效区产生异于正常区的动力特性。轨下支承刚度沿轨道纵向的改变会增大空吊区附近的轨道支承力。激增的轮轨接触力将对桥梁和轨道产生突变的加速度,进一步造成道床脱空、轨道几何不平顺的局部永久变形、钢轨扣件的支承失效和桥梁局部的损伤破坏。因此,列车通过轨下支承失效区域将会恶化线路和桥梁的运营状态。若不能及时维修破损的线路,轨下支承受损段将威胁列车的平稳运行和影响乘客的舒适性,甚至严重破坏段会引发列车脱轨等重大安全事故。

目前,轨下支承失效对系统的动力响应分析主要包括试验和数值仿真2种方式。S.L.GRASSIE[1]利用试验数据,计算轨道支承的刚度和阻尼参数,基于数值仿真来研究轨枕空吊对轨道产生的动力影响,结果表明,轨枕空吊会显著增大动态接触力,加速轨道的恶化速度;J.A.ZAKERI[2]研究了轨道在完全支承、部分支承和空吊下的位移和轮轨接触力,表明3个连续的轨枕空吊对轨道位移有显著影响;DAI Jian[3]研究了轨枕的空吊数量、空吊形式和不同的行车速度对轨道接触力峰值位置的影响,指出最大轮轨接触力取决于行车速度和在不同间隔的轨枕空吊缺陷之间完全支承的轨枕数量;SHI Jin[4]以朔黄重载铁路线为研究对象,建立了一个包含轮轨摩擦的三维动力有限元模型,研究指出,随着轨枕空吊数量的增加,轨枕和轨枕扣件等轨道系统成分和与轨枕空吊相邻的路基部分可能会出现提早破坏而失去承载能力;ZHU Jianjun[5]提出了一种基于中心有限差分法的数值模拟方法,并采用该方法计算轮轨接触模型,仿真结果表明,轮轨间的冲击载荷取决于无支承的轨枕数量、车辆速度和道枕与道床之间的间隙大小;ZHU Jianyue[6]进行1∶5 比例的轮轨模型试验,研究指出,轨道加速度的频响函数在跨中出现峰值,并在轨枕上方出现陡倾,道砟是铁路轨道的重要阻尼源,低频时道枕的振动幅值最大,当轨枕完全空吊时,其振动几乎是无阻尼的;张大伟等[7]基于非线性作用力建立重载铁路轨枕空吊的动力响应模型,分析了不同轨枕空吊状态和列车运行速度对轮轨垂向作用力的影响,得出轮轨垂向力随空吊数量的增加与列车运行速度的提高而显著增大的结论;邹春华等[8]基于1∶1室内有砟轨道试验,以路基不均匀沉降作为非线性边界条件,建立连续弹性点支承模型,提出了路基不均匀沉降引起的轨枕空吊计算方法;张健等[9]利用显式积分法求解非线性动力的车辆-轨道耦合方程,探讨了轨枕不同悬空状态时轨枕中间截面的弯矩变化规律。

首先,笔者基于虚功原理推导了包含轨下支承失效的列车-轨道-桥梁耦合方程。轨道与桥梁之间的耦合采用单层离散点支承的弹簧阻尼,以各轨枕位置作为离散支承点,将轨道与轨枕视为一体。车辆模型在轮对沉浮自由度上采用Hertz弹性接触与轨道耦合。然后,利用现有文献的参数与解析解比较分析,评价文中计算模型的准确性。最后,对计算模型进行参数化研究,把轨下支承正常与不同病害程度的轨下支承失效作为工况条件,分析轨道和桥梁的动力响应特性及轮轨接触力的变化规律。多数文献将轨道下方结构均视为路基部分,建立车辆-轨道耦合的计算模型。鉴于此,将轨道和桥梁一起建模,分析轨下支承失效对桥梁和轨道结构动力响应的文献相对较少。笔者所建立的列车-轨道-桥梁耦合的动力学模型更能充分反映轨下支承失效对轨道和桥梁结构的变化规律,以期为轨道和桥梁系统的运营、养护提供参考依据。

1 基于虚功原理的车-轨-桥动力耦合方程

首先,基于虚功原理建立了不含轨下支承失效的列车-轨道-桥梁耦合的动力方程。轮轨之间和桥轨之间的相互作用力体现了3个子方程之间的动力耦合关系,实现子方程耦合。其次,假设轨道和桥梁丧失相互作用力来模拟轨下支承失效,即去除轨下支承失效区域的桥轨耦合项。轨下支承失效的车-轨-桥耦合动力学计算模型如图1。

图1 轨下支承失效的车辆-轨道-桥梁耦合模型示意Fig. 1 Schematic diagram of vehicle-track-bridge coupling model with under-rail support failure

笔者建立的车-轨-桥耦合动力学模型基于以下5个假定:①轨道和桥梁均为弹性体、均质体和各向同性体,采用平面Euler-Bernoulli梁来模拟;②轮轨接触面积是一个小的椭圆区域,采用线性化的Hertz接触理论模拟轮轨几何关系[10];③车辆模型采用四轴二系悬挂,每个车辆共有10个自由度,即车体和每个转向架考虑沉浮和点头自由度,每个轮对考虑沉浮自由度;④轮对、转向架和车体沿桥跨方向做匀速运动,不考虑每辆列车之间的纵向连接和纵向振动的影响;⑤轨道采用离散的弹簧阻尼支承连续梁模型,左右二股钢轨视为一体。

考虑轮轨接触不存在拉力,避免将轮轨接触和轮轨脱离2种工况分开建模。基于假定②将轮轨Hertz接触的线性弹性刚度系数统一表示为akvr,接触系数a应满足式(1):

(1)

式中:yj为在t时刻第j个轮对处的几何相容性条件。yj如式(2):

yj=Sj,t-Lr-R

(2)

式中:Sj,t为在t时刻第j个轮对的沉浮;Lr为轨道在接触点x和当t时刻的竖向位移;R为第j个轮对在接触点x的轨道竖向几何不平顺。

基于虚功原理推导的轨道单元动力方程可表达为:

(3)

基于虚功原理推导的桥梁单元动力方程可表达为:

(4)

车辆动力方程的表达参考文献[12]。轮对的沉浮自由度通过Hertz接触弹簧与轨道单元的竖向自由度进行耦合连接。因此,只需修正轮对的沉浮自由度及其轮轨耦合项:

(5)

(6)

由“对号入座”法组装单元矩阵,便可列出列车-轨道-桥梁耦合系统的竖向振动方程,其单元子矩阵的形式如式(7):

(7)

当轨下基础支承刚度和阻尼沿轨道纵向不均匀变化时,只需对模型中各支点刚度和阻尼元件逐一赋值,即可输入各种弹性动力不平顺[13]。在轨枕支承失效的位置,去除轨枕下部的弹簧-阻尼单元,即可令该支点处krb=crb=0。

式(7)中,轨道和桥梁单元及其耦合项的矩阵均是非时变的,而车辆和轨道单元及其耦合项的矩阵均是时变的。在每个时间积分步里,判断轮轨接触或轮轨脱离,将非时变矩阵和时变矩阵叠加便可得到系统的动力方程。再利用Newmark方法直接积分求解时程曲线。在MATLAB软件编写了相应的计算程序。

2 簧上质量过简支梁桥的解析解验证

选取文献[14]算例进行分析,如图2。簧上质量块从梁左端向右运动,模型参数如下:弹性模量Eb=2.87 GPa;截面惯性矩Ib=2.90 m4;跨径s=25 m;单位长质量mb=2 303 kg/m;质量块质量mv=5 757 kg,悬挂刚度k1=1 595 kN/m,移动速度v=27.78 m/s。桥的振动频率为ωb=30.02 rad/s,簧载质量的频率ωv=16.66 rad/s。 车辆简化为车身的沉浮自由度即l/4 弹簧质量模型,忽略悬挂和桥梁阻尼的影响。

图2 簧上质量过简支梁桥模型Fig. 2 Model of a moving sprung mass through a simply supported beam bridge

质量块和桥梁耦合的动力方程由Biggs导出[15]。对于桥梁的动力响应,Biggs推导的解析解只考虑桥梁的一阶模态,如式(9):

(8)

式中:

(9)

将Biggs解析解、移动荷载解析解[16-17]与文中解进行对比,得到桥梁跨中的竖向位移、速度和加速度的动力响应如图3～图5。由图3～图5可知,移动荷载解析解与Biggs解析解、文中解的计算结果出现偏差。因为考虑车桥耦合作用与移动荷载相比,前者致桥振动的能量更大。而文中算法计算的桥梁跨中竖向位移响应与Biggs推导的一阶模态解非常吻合。在简支梁跨中的垂直速度响应和垂直加速度响应中,文中解与Biggs解有较高的吻合程度,但两者仍存在微小的相位差。同时文中解在加速度响应中出现了高频振荡。这可以理解为由于Biggs解析解忽略了车辆振动产生的能量对桥梁高阶模态的激励,而高阶模态对桥梁的速度响应和加速度响应存在影响。因此,桥梁动力响应的精确计算结果不可忽略高阶模态。笔者基于虚功原理推导的车-轨-桥耦合有限元法能考虑在耦合作用下输入桥梁的能量所激发的高阶模态。

图3 桥梁跨中位移时程曲线Fig. 3 Time-history curve of mid-span displacement of bridge

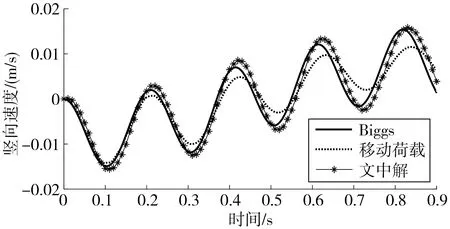
图4 桥梁跨中速度时程曲线Fig. 4 Time-history curve of mid-span velocity of bridge

图5 桥梁跨中加速度时程曲线Fig. 5 Time-history curve of mid-span acceleration of bridge

3 轨下基础结构缺陷对轨道和桥梁的动力响应分析

参照我国高速铁路某双线简支箱梁桥图纸,桥梁结构参数如下:跨径s=32 m;弹性模量Eb=34.5 GPa;惯性矩Ib=11.1 m4;单位长度质量mb=43 630 kg/m;采用Rayleigh阻尼,阻尼比ζ=0.02[18];Hertz接触刚度为5×108N/m;桥梁一阶频率为4.6 Hz;理论共振车速为108 m/s,考虑v=100 m/s接近共振车速;过渡段路基取12 m;钢轨单元长度可取为2倍轨枕间距,故钢轨单元长度取1.2 m[19]。列车编组考虑5辆车匀速通过轨道。其中车辆和轨道的结构参数取值参考文献[20]。

轨下基础结构缺陷的位置及观测点示意如图6。笔者分别选取了桥梁段和路基段的2个连续轨下支承失效与轨下支承结构完整的工况,对毗邻轨下基础结构缺陷区的过渡段中点(观测点O)和桥梁跨中(观测点Q)进行动力响应时程仿真分析。由于轨下基础结构缺陷本质上是动力型不平顺,轮对或钢轨的几何不平顺相对于动力型不平顺所造成的振幅可以忽略。因此,笔者只考虑轨下基础结构缺陷,而不考虑几何不平顺对动力的影响。

图6轨下基础结构缺陷的位置及观测点示意 Fig. 6 Schematic diagram of the defect location and observation point of the infrastructure under the rail

观测点Q的桥梁位移时程曲线如图7,观测点Q的桥梁加速度时程曲线如图8。由图7、图8可知,当列车通过桥梁段时,1个轨下支承失效与轨下正常支承相比,桥梁跨中的位移响应并未产生明显的偏差,两条曲线几乎重合。但是,轨下基础结构缺陷会对桥梁跨中的加速度产生高频振荡。1个轨下支承失效时,桥梁跨中的最大加速度为0.622 1 m/s2,相比于轨道正常支承状态下的最大加速度0.425 2 m/s2,增大到约1.46倍。这是因为轨下基础结构缺陷处轨道与桥梁失去了耦合作用,导致轨下基础结构缺陷区域附近的桥轨耦合作用力突增,使桥梁跨中的加速度明显增大。

图7 观测点Q的桥梁位移时程曲线Fig. 7 Bridge displacement time-history curve at observation point Q

图8 观测点Q的桥梁加速度时程曲线Fig. 8 Bridge acceleration time-history curve at observation point Q

观测点Q的轮轨竖向接触力如图9。由图9可知,轮轨相互作用力是时变的,开始时刻轮轨相互作用力变化剧烈的原因在于车辆突然施加荷载给轨道。当车辆平稳运行,轮轨竖向接触力在轨道支承完好时呈现周期性变化,作用力的峰值达到140.5 kN。而列车经过轨下基础结构缺陷处时,由于轨道丧失支承力,产生余弦型不均匀沉降,引起轮轨间的局部高频振动。车体突变的加速度产生非周期性变化的惯性力,轮轨相对位移的突变导致非周期性变化的Hertz 接触弹性力。此时,轮轨竖向接触力的峰值达到179.2 kN,较轨下正常支承时增大了27.54%。

图9 观测点Q的轮轨竖向接触力Fig. 9 Wheel-rail vertical contact force at observation point Q

随着轨下支承失效的数量增加,轨下结构的缺陷变得越来越严重。观测点Q在不同数量轨下支承失效下桥梁加速度与轮轨竖向接触力如图10。由图10可知:在相同速度下,当发生1～2个轨下支承失效时,桥梁跨中加速度分别为0.622 1、0.960 4 m/s2,较轨道良好支承时的0.425 2 m/s2,分别增大了46.31%、125.87%;轮轨竖向接触力峰值分别为140.5、179.2 kN,较静轮重134.63 kN,分别增大了4.36%、33.11%。轨下支承失效2个时,桥梁最大加速度和轮轨竖向接触力峰值均显著增加。这说明轨下基础结构缺陷造成的动力性不平顺会导致缺陷区的轮轨接触点基本失去了轨道垫层的缓冲作用,增大了临近缺陷区的动力响应。当列车荷载反复作用于轨下基础结构缺陷区,加剧对此范围附近桥梁构件的疲劳损伤程度,严重时可能危害桥梁的运营安全。

图10 观测点Q在不同数量轨下支承失效下桥梁加速度与轮轨竖向接触力Fig. 10 Bridge acceleration and wheel-rail vertical force under different numbers of under-rail bearing failures at observation point Q

过渡段的轨道结构直接由路基支承,选择过渡段路基中点处的1个轨下支承失效与轨下正常支承进行对比分析。列车运行速度同为100 m/s,轨道时程分析选取毗邻缺陷处的观测点O。观测点O的轨道位移对比如图11,观测点O的轨道加速度对比如图12。由图11、图12可知:当轨下支承完好时,轨道的最大竖向位移为0.417 mm,最大竖向加速度为15.43 m/s2;当发生1个轨下支承失效时,轨道的最大竖向位移为0.665 mm,最大竖向加速度为26.28 m/s2,分别是轨道无病害时的1.594倍和1.703倍。这说明高速列车致轨道振动时,轨道下部结构对轨道承受的冲击起到明显的减缓作用。当列车通过轨下支承失效区域,轮轨作用力由毗邻轨下基础结构缺陷区的正常支承区段分担,而使观测点O处的轨道位移和加速度振幅显著增大。

图11 观测点O的轨道位移对比Fig. 11 Orbital displacement comparison diagram of observation point O

图12 观测点O的轨道加速度对比Fig. 12 Orbital acceleration comparison diagram of observation point O

为进一步说明行车速度的差异和轨下基础结构缺陷的病害程度对轨道的冲击作用。观测点O的轨道位移响应随列车行车速度和轨下支承失效数量的变化规律如图13,观测点O的轨道加速度响应随列车速度和轨下支承失效数量的变化规律如图14。由图13、图14可知,轨下基础结构缺陷的病害程度越严重,即轨下支承失效的数量越多,轨道的位移和加速度随行车速度的增加而急剧增大。当发生2个轨下支承失效,且行车速度为20 m/s时,轨道的最大位移为1.388 mm、最大加速度达到2.073 m/s2;行车速度为80 m/s时,轨道的最大位移为1.605 mm,增大了约15.6%;行车速度为100 m/s时,最大加速度达到68.7 m/s2,增大了约32倍。这表明行车速度与轨下支承失效数量相比,行车速度对轨道加速度的影响更加剧烈,而轨下支承失效数量对轨道位移的影响更明显。因此,列车应低速通过轨下基础结构缺陷区域。轨道线路的日常管养应及时发现并修缮受损区,避免轨下结构缺陷的区域进一步向临近的正常区域扩展,造成轨道在剧烈的振动下出现损伤破坏。

图13 观测点O的轨道位移响应随列车行车速度和轨下支承失效数量的变化规律Fig. 13 Variation law of the track displacement response at observation point O changing with the train speed and the number of under-rail support failures

图14 观测点O的轨道加速度响应随列车行车速度和轨下支承失效数量的变化规律Fig. 14 Variation law of the track acceleration response at observation point O changing with the train speed and the number of under-rail support failures

4 结 论

基于虚功原理分别建立了桥梁单元和轨道单元的动力耦合方程,并对车辆动力方程中的沉浮自由度及轮轨耦合项加以修正,将各子方程按“对号入座”法组装车-轨-桥耦合矩阵。当轨下支承缺陷时,通过去除桥轨离散连接的弹簧-阻尼耦合项,进而修正原始组装的车-轨-桥系统矩阵。利用该模型探讨了轨下支承失效的条件下轮轨竖向接触力、桥梁和轨道的动力响应变化规律。结果表明:

1)基于虚功原理建立的车-轨-桥耦合有限元计算模型与解析解相比吻合度较高。轨下支承失效区域通过去除桥轨连接的弹簧-阻尼耦合矩阵项来修正原始矩阵的方式是合理可行的。

2)轨下基础支承缺陷对桥梁的位移响应影响较小,但会加剧桥梁的加速度响应。

3)车辆平稳运行时,轮轨竖向接触力在轨道下方被道床良好支承时呈现周期性变化,而列车经过轨下结构缺陷区域时,轮轨作用力会发生突变。

4)当出现1个轨下支承失效时,轨道竖向位移和加速度动力响应变化较小。当病害发展到2个轨下支承失效时,轨道竖向位移和加速度动力响应变化显著增大。同时,列车行车速度的提高对轨道动力响应的变化非常剧烈,速度效应十分明显。因此,铁路部门应及时发现并修复轨下基础支承缺陷的病害,提醒列车司机低速通过病害区域。