重载铁路轨下弹性垫板外形对轨枕承轨槽磨损影响研究
李敏一,戴佳程,陈 嵘,刘鉴兴,肖杰灵,王 平
(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031;2.西南交通大学土木工程学院,成都 610031)
引言
随着我国重载铁路的蓬勃发展,轴重和运量均在不断加大,对轨道结构的服役性能和使用寿命提出了重大挑战[1-2]。我国的重载运输铁路均不同程度的面临挖潜增能的压力,提高运能.增加轴重势必要求基础设施能承受更大的作用力.具有更好的工作性能和更长的服役寿命。重载列车的大轴重.大运量对线路结构破坏较大,轨道几何状态难以保持,道床板结程度严重,受限于时空因素及维护条件制约,道床清筛维护困难,轨道结构的弹性很大程度上需要依靠轨下垫板来提供[3]。但在大轴重轮载的反复作用下,轨下弹性垫板与轨枕承轨槽发生磨损,部分轨枕切槽病害严重[4],进一步恶化了轨道结构服役状态,如图1所示。

图1 轨枕承轨槽磨损
针对材料磨损问题,李文丽[5]利用ADAMS仿真软件基于Archard磨损模型对运动副不同接触点的磨损量进行计算,表明复杂的磨损过程可通过仿真试验预测其可靠性;宫昱滨[6]通过对能耗法进行修正并结合非线性有限元软件Abaqus的自适应网格技术,对圆柱—平面微动磨损装置进行了仿真分析,预测磨损斑宽度;赵亚元[7].李良[8].胡海明等[9]基于Archard磨损模型对各工况下轮胎橡胶与地面磨损仿真,准确获得了胎面磨损特点,表明对于橡胶这种不可压缩材料磨损具有仿真可行性。
轨枕承轨槽磨损一旦产生,会加速与之接触的橡胶垫板的磨损,橡胶垫板磨损反之进一步加剧轨枕承轨槽磨损[10]。磨损过程是不断劣化发展的过程,既是一种微观现象,也是一个宏观过程。材料的磨损与许多微观因素有关,如接触表面的局部摩擦系数.局部温度.局部相对滑移速度等[11]。大多数结构摩擦表面在整个使用过程中都会经历长时间的高应力.非线性磨损过程。轨下弹性垫板与轨枕承轨槽是重载铁路大轴重.大运量条件下的典型轨道结构摩擦副。通过探索高效.可靠的数值计算方法,预测不同外形方案的轨下弹性垫板与轨枕承轨槽的微动磨损行为,分析磨损量及磨损状态分布规律,为部件优化设计和重载铁路轨道结构强化提供理论参考。
1 垫板/承轨槽磨损模型
1.1 Archard磨损本构模型
20世纪50年代,摩擦学界著名学者J.F.Archard的研究成果提出Archard磨损法。Archard模型中需要明确摩擦接触表面的接触条件,包括接触压力.相对滑移距离等,还需要确定接触对的磨损系数等摩擦学参数[12]。当接触面间的摩擦系数不是定值时,Archard模型很难对磨损进行较为合理的定量计算[13],但正压力在试验中容易获得,该模型提出后便被广泛应用到磨损试验研究中。基于Archard磨损模型来预测界面的磨损是近年来被广泛应用的仿真分析手段。磨损过程中,材料磨损体积V被认为正比于接触面法向荷载[14]。模型的数学表达式如下
(1)
式中,V为材料磨损体积,S为相对滑移距离,K为无量纲的磨损常数,H为接触对中较软材料的布氏硬度,FN为接触面法向荷载。
由于仿真计算存在局限性,模型作出以下假设:
(1)预测的磨损状态遵循塑性磨损机理,忽略摩擦表面生热;
(2)忽略磨屑的作用;
(3)摩擦系数和磨损系数无变化。
1.2 有限元仿真模型
1.2.1 几何尺寸更新实现
有限元磨损仿真的难点在于轨下垫板与轨枕的接触表面轮廓随着磨损的进行发生改变,这会导致接触区域接触应力发生改变[15],从而引起磨损量的实时变化。使用FORTRAN语言编写适用于有限元模型和网格划分的子程序UMESHMOTION[16]。子程序自定义网格调整量,调取各个ALE(自适应网格)节点的接触压力和相对滑移距离,按照Archard磨损模型计算磨损量后,更新节点坐标[17-18]。利用求解器提供的自适应网格技术[19-20]调整网格以表征微动磨损。其计算包括2个内容:通过Sweeping技术创建新网格;Advection使计算变量转移新网格。
垫板/承轨槽磨损模型具体步骤如下:
(1)建立有限元磨损模型,定义材料属性,荷载,边界条件,增量步等;
(2)在ABAQUS中对有限元模型进行分析计算,提取接触区域各个节点处的接触应力及相对滑移距离;
(3)每个增量步收敛后,调用UMESHMOTION子程序,先根据Archard模型计算出每个节点的磨损深度和磨损体积,然后根据指定的磨损变化方向对节点位置调整;
(4)节点更新后生成新的表面轮廓,如此循环,当满足要求后停止仿真。
1.2.2 有限元模型
轨下垫板采用3种不同外形,第1种为上下表面全带沟槽的轨下垫板,第2种为上下表面均无沟槽的轨下垫板,第3种为上表面带沟槽但下表面不带沟槽的轨下垫板,如图2所示。为节省计算时间,只取部分轨枕,轨下垫板放置于混凝土轨枕块之上,混凝土轨枕块尺寸稍大于轨下垫板。为模拟实际重载线路上轨下垫板下表面与混凝土轨枕承轨槽上表面的接触作用,使用“面—面”接触方式定义,设定为“小滑移”。对混凝土轨枕块下表面的节点全约束。对于橡胶类体积不可压缩材料使用Herrmann单元,避免体积自锁。分析轨下垫板有无开槽对轨枕磨损产生的影响,有限元模型如图3所示。

图2 3种不同外形的轨下垫板
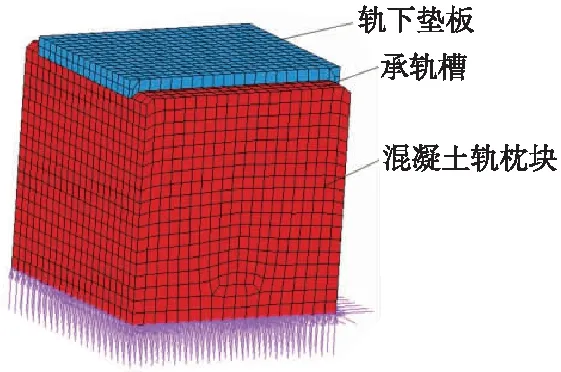
图3 轨下垫板/承轨槽磨损模型
1.2.3 有限元模型相关参数
根据相关资料,重载线上货车轴重25 t,单个轮载为125 kN,再考虑2倍的动力系数,可得动轮载为187.5 kN。根据枕上压力的公式计算可得单根枕上最大压力为Rmax=127.5 kN。该值将作为有限元模型的最不利枕上压力值用于计算中。该磨损量的计算依托于有限元仿真计算软件,在参数的选取上格外注意,最大程度上达到有效模拟材料的相关特性要求。有限元模型仿真计算时间为10 s,有限元模型计算参数见表1。

表1 有限元模型计算参数
1.2.4 计算工况
本次建模仿真是为计算轨下垫板和轨枕作用的磨损量,故工况相对简单,各工况的区别在于垫板硬度不同(为方便计算采用布氏硬度)或其杨氏模量不同,其他加载条件及约束情况完全一致,具体见表2。

表2 计算工况
2 结果分析与讨论
2.1 接触面磨损分布
选取轨下垫板杨氏模量为16 000 MPa,布氏硬度为80 HB时轨下垫板与轨枕接触面磨损量云图进行分析,如图4所示,磨损云图能够较为准确预测磨损位置。轨枕和轨下垫板潜在的最大磨损量出现在接触面的边缘区域,磨损量越靠近接触中心就越小,接触中心无磨损。
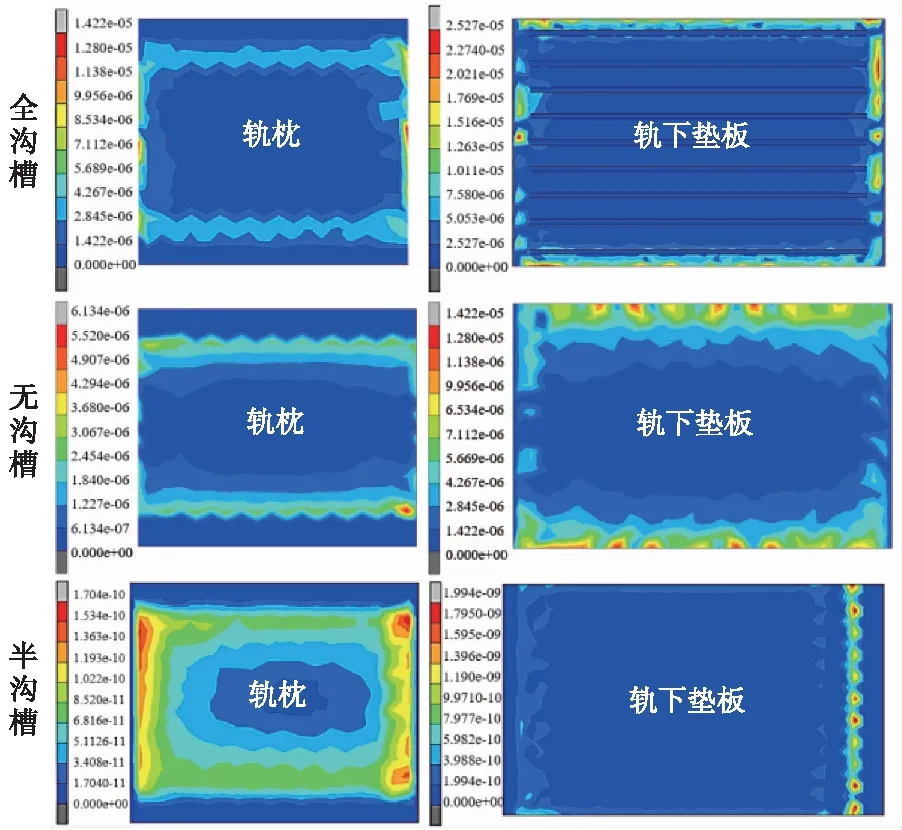
图4 3种轨下垫板与轨枕之间的磨损云图
全沟槽轨下垫板易发生应力集中,接触面磨损云图极不规则,垫板潜在的磨损出现在接触面的边缘,最大磨损量在沿轨枕长度方向的接触面两侧处,接触中心部分磨损量较小;无沟槽轨下垫板,轨枕承受荷载时应力的流线均匀变化,所以轨枕磨损云图呈梯度变化;半沟槽轨下垫板,轨枕上最大磨损深度发生在与垫板接触的四个角处,虽然轨枕磨损区域大(只有接触中心很小部分未发生磨损),但最大磨损量远小于其他2种垫板。
2.2 硬度对磨损行为的影响
只改变轨下垫板布氏硬度后,如图5所示,采用全沟槽轨下垫板时,轨枕总磨损量随硬度增加磨损量趋于稳定;采用无沟槽轨下垫板时,轨枕总磨损量随布氏硬度变化影响较大,垫板硬度为800 HB时轨枕总磨损最小;采用半沟槽轨下垫板时,轨枕总磨损随布氏硬度增加无明显变化,半沟槽轨下垫板总磨损量远小于其他2种垫板。

图5 轨枕总磨损深度对数坐标
如图6所示,改变轨下垫板布氏硬度后,无沟槽轨下垫板总磨损量随轨下垫板硬度增加,轨下垫板磨损总量先剧烈降低,在硬度为800 HB时趋于稳定,其他2种垫板的总磨损量均随着布氏硬度的增大急剧减小。此外,采用半沟槽垫板时垫板总磨损量最小。
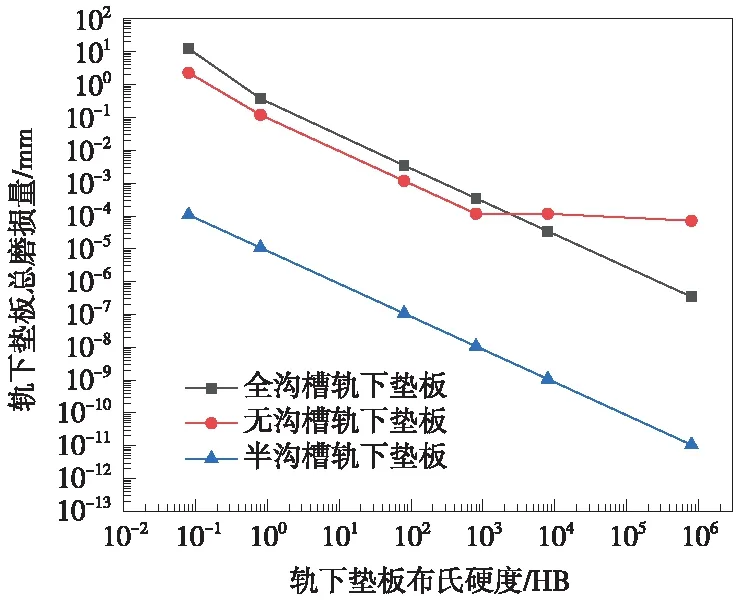
图6 轨下垫板总磨损深度对数坐标
2.3 杨氏模量对磨损量的影响
只改变轨下垫板杨氏模量时,如图7所示,采用全沟槽轨下垫板,轨枕总磨损量随杨氏模量80~8 000 MPa剧烈下降;采用无沟槽轨下垫板,轨枕总磨损量变化轻微,当垫板杨氏模量在8 000 MPa时轨枕总磨损量处于谷值;采用半沟槽轨下垫板,轨枕总磨损量随着杨氏模量增长保持无明显变化,并且半沟槽轨下垫板总磨损量远小于其他2种垫板。
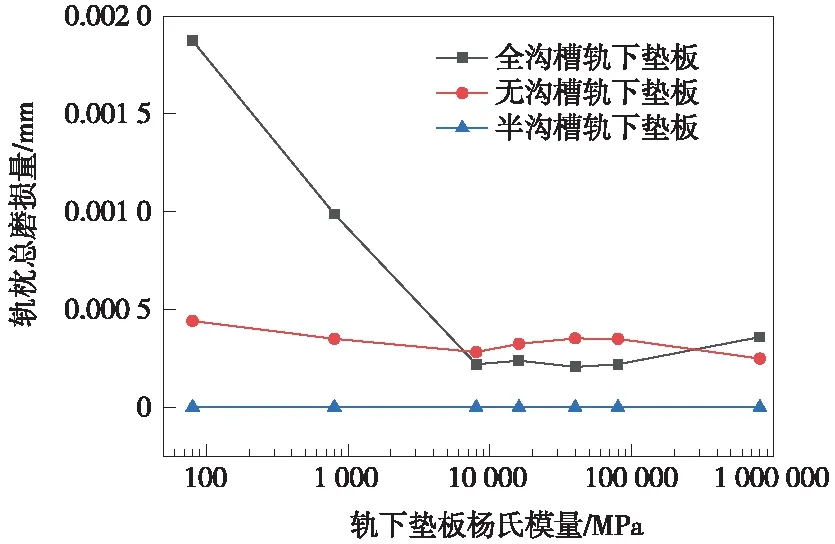
图7 轨枕总磨损深度对数坐标
如图8所示,改变轨下垫板杨氏模量后,轨下垫板总磨损量在杨氏模量为8 000 MPa时均为3种垫板总磨损量的拐点,且全沟槽轨下垫板总磨损量始终最大,半沟槽轨下垫板总磨损量始终最小。
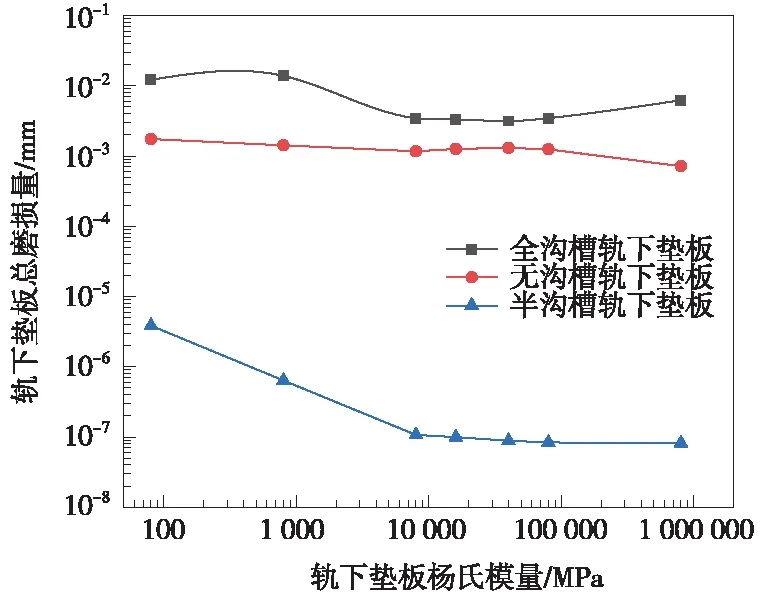
图8 轨下垫板总磨损深度对数坐标
3 结论
基于Archard磨损模型对轨下弹性垫板与轨枕承轨槽进行动态磨损仿真分析,得到结论如下。
(1)由于轨下垫板与轨枕承轨槽真实磨损试验成本高.周期长,难以实施,采用磨损仿真方法计算磨损深度和预测磨损位置,为轨下垫板设计提供了新的思路。
(2)潜在的磨损出现在轨下垫板与轨枕接触面边缘,接触面中心由于相对滑移为零导致无磨损。
(3)相较于其他2种垫板,采用半沟槽轨下垫板后,虽然受磨损区域大,但轨枕表面磨损量微小,产生的总磨损量远小于其他2种垫板产生的磨损量。采用全沟槽轨下垫板产生的总磨损量最大。
(4)综合考虑制作工艺和经济成本,轨下垫板硬度取80~800 HB区间内,轨下垫板杨氏模量取8 000 MPa附近时,轨下垫板与轨枕的磨损量均处于较理想的水平。
(5)本文涉及的磨损问题仅处于初探阶段,目前尚不清楚摩擦系数.磨损系数和忽略磨屑等带来的不确定影响,有待深入研究。

