高速铁路牵引供电系统间谐波的机理与特征研究

崔玮辰，刘明光，郑景文

(1.北京交通大学电气工程学院，北京 100044；2.中车青岛四方机车车辆股份有限公司，青岛 266000)

引言

以HXD系列重载电力机车和CRH系列高速动车组为代表的交直交电力机车具有牵引力大.运行速度高的特点，极大地促进了铁路大发展。但在实际运营中也发生了车网电气耦合产生的谐波与间谐波问题，如：2007年京哈线蓟县南牵引变电所两侧供电臂电压波动高达35～75 kV，远远超过27.5 kV的正常电压水平[1]；2010年海南东环线博鳌牵引变电所和琼海分区所均发现了严重谐波畸变情况，接触网谐波电压畸变达到24%，并呈现出一定的周期性[2]；2011年京沪高铁先导段固镇变电所向蚌埠越区供电时，牵引网存在55次附近谐波电流放大现象，该区段的牵引取流曾引起谐振过电压，导致动车组因过电压多次跳主断.1次避雷器烧损[2]；2016年上海南翔动车所同一供电区段CRH380B动车组跳主断保护，造成列车晚点[3]；2018年迁曹线曹妃甸宫殿区段接触网避雷网炸裂，机车RC支路电阻烧损[4]。

已有大量国内外学者从谐波谐振特性[5-6].谐波特性建模[7].谐振敏感度[8]和谐振抑制[9]等角度对产生频率为基波频率整数倍的谐波进行了研究，但对于范围更广的.产生频率为基波频率非整数倍的间谐波研究报道甚少。间谐波较谐波而言存在范围更广，对铁路供电质量的影响同样需要引起重视。

IEC61000-2-1标准将间谐波定义为非整数倍基波频率的电压或电流信号。间谐波作为铁路供电电能质量的重要指标，允许含量较谐波而言更为苛刻，与基波的叠加更为复杂，合成波形的周期更为不规律。同时由于间谐波的存在，还会造成电压的波动与闪变.间谐波谐振.无源滤波器过载.电压波形过零点偏移等影响[10]。因此，研究高速铁路牵引供电系统间谐波的机理与特性，对预防牵引网间谐波危害，确保电力机车的行车安全具有重要意义。

从电力系统背景间谐波.铁磁元件非线性特性.牵引网阻频特性及电力机车回路特性，分析高速铁路牵引供电系统间谐波产生的机理，并借助PSCAD仿真软件搭建高速铁路牵引供电系统的联合仿真模型，求解牵引网的特征阻抗，仿真对比电力机车在不同工况.不同位置时系统间谐波的分布情况，可为高速铁路牵引供电系统间谐波的研究提供参考。

1 牵引供电系统间谐波机理分析

1.1 电力系统背景间谐波

高速铁路牵引供电系统与电力系统相连，其牵引变电所可将电力系统的三相110.220 kV(330 kV)交流电转变为单相25 kV交流电供给牵引网。电力系统作为供电来源，本身会存在一定的间谐波，对某供电地区在不同典型负荷下进行电能质量检测，得到间谐波电流的幅值.相位.与基波电流比值的结果如表1所示，测得幅值含量大于1%的间谐波有41.59.240.254 Hz等[11]。这些电力系统中存在的间谐波一定程度上会通过牵引变压器扩散到牵引供电系统中。已被证实的间谐波来源有变频装置.波动负载.电弧类负载和感应电动机等[10]。除此之外，在牵引供电系统中还应重视诱发间谐波的各种因素。

表1 某供电地区电流间谐波分布

1.2 铁磁元件非线性特性诱发的间谐波

牵引供电系统中含有大量的电压互感器，由于电压互感器是带铁芯的电感元件，容量相对较小，振荡则会引起铁芯饱和，从而发生非线性自激振荡，进而产生一定频率的间谐波。其原理及相应的伏安特性均可等效为图1所示的电路和曲线[12]，图中电源电势E.电阻R.电容C.电感L均为等效后取值。电容伏安特性UC为斜率103C9/C的直线，铁芯电感的饱和特性使得电感伏安特性UL为曲线，UC与UL的交点为谐振点P。

若忽略回路中的电阻，当E=|UL-UC|=ΔU时，可求得3个平衡点s1.s2.s3，通过扰动法可判定s1.s3为稳定平衡点，s2为不稳定平衡点。当系统电源电势在额定电压E附近时，该回路会工作在稳定平衡点s1；当系统因振荡出现一定的暂态过电压时，将引起电压互感器铁芯饱和，电感值减小，电流值增加，工作点运动到s2点；由于s2为不稳定平衡点，电感值将继续减小，电流值继续增加，工作点运动到谐振点P；易知，P点仍不能稳定存在，最终系统将到达新的工作点s3。考虑回路电阻的阻尼作用，会使图1中直线E下降，稳定平衡点s1和s3的电流值相应减小，谐振状态的电流幅值减小，电感.电容的电压降低，会减小谐振的发生。

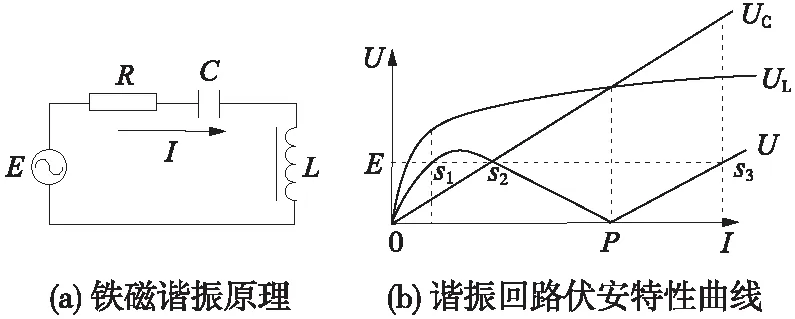
图1 铁磁谐振原理及谐振回路伏安特性曲线

在实际运行中，存在一些因素会导致电压处于偏高状态，如：为保证线路末端电压满足机车供电需求，牵引变压器供电端的电压需要抬高10%；空载线路时，末端电压会出现偏高情况；车载断路器分合闸时会产生过电压。这些偏高电压情况极有可能促使电压互感器这类铁磁元件的工作点进入非线性饱和区域，从而诱发间谐波。此外，由于回路中具体参数不同，产生的间谐波可为特定的不同频率。

1.3 牵引网阻频特性与间谐波的关系

牵引网是由电阻.电感及电容构成的复杂串并联电路，在车网耦合过程中，除了带来谐波问题，还会产生间谐波，通常等效为如图2所示的电路模型[13]。

图2 牵引网等效电路

图2中，iS为机车等效的电流源；ZS为牵引变压器等效到牵引网侧的阻抗；ZP为分区所阻抗；ZLE.ZRE分别为左.右侧牵引网阻抗；ZL.ZR和YL.YR分别为左.右侧牵引网等效阻抗与导纳，公式如下

(1)

机车端口处的牵引网等效阻抗Zi为ZLE和ZRE的并联，化简得

Zi=

(2)

牵引网发生并联谐振的条件为lm[Yi(jω0)]=0(Yi为Zi的导纳)，对应Zi的分母应为零，化简得到并联谐振频率f0为

(3)

式中，LS.Lp分别对应ZS.Zp的电感值；L.C分别对应Z.Y的电感.电容值。

由式(2).式(3)可知，牵引网的阻频特性与牵引网自身结构参数及供电臂长度有关，发生并联谐振时的频率可以是特定的谐波或间谐波。

1.4 电力机车诱发的间谐波

交直交型电力机车作为牵引供电系统移动的非线性负荷，是牵引供电系统中产生谐波与间谐波的主要来源。其通过车载变压器，将牵引网接入的25 kV单相工频交流电变成低压交流电，经四象限整流器与逆变器把低压交流电转换成频率和幅值均可调节的三相交流电，用来驱动三相异步牵引电动机，其原理等效为图3所示的模型。

图3 交直交型电力机车等效模型

1.4.1 车载直流侧—牵引网交流侧间谐波模型

单相PWM整流器作为交直交型电力机车牵引传动系统的重要组成部分，其拓扑结构和控制算法对机车的谐波.间谐波特性有决定性影响[14]。其中，CRH3型电力机车采用的是单相两电平PWM整流器，其主电路的原理如图4所示[15]。

图4 单相两电平PWM整流器原理

根据双重傅里叶变换[16]，可求得单相两电平PWM整流器的开关函数Sab的表达式

Sab=Sa-Sb=Mcos(ωmt+φm)+

cos(nωmt+mωct+nφm+mφc)

(4)

式中，M为调制波幅值；ωm为调制波的角频率；φm为调制波的初相角；ωc为载波的角频率；φc为载波的初相角；Jn为n阶贝塞尔函数。

在实际运行中，车载设备直流侧电压中会含有不同频率的纹波，以单一纹波为例，设直流电流为

idc=Idc[1+kcos(ωht+φh)]

(5)

式中，k为纹波电流幅值与直流常量Idc的比值；ωh为纹波电流的角频率；φh为纹波电流的初相角。

根据变流器开关函数理论[17]，可得牵引网电流is的推导式为

is=idcSab

(6)

直流电流包含两个部分，Idc为直流常量，kIdc×cos(ωht+φh)为波动分量。波动分量与开关函数相乘后将会在网侧电流中产生新的谐波或间谐波。根据式(5).式(6)可知，开关函数Sab包含基波分量与谐波分量，将直流电流分别与Sab的基波分量和谐波分量相乘，得到结果之和便是最终牵引网交流侧的电流。其计算公式如下。

①与Sab基波分量相乘得到式(7)

is=MIdccos(ωmt+φm)+

cos[(ωm-ωh)t+φm-φh]}

(7)

由式(7)可以看出，得到的牵引网电流中，除了基波角频率ωm外，还产生了新的角频率ωm±ωh，当ωh不是基波整数倍的角频率时，通过PWM整流器将会在牵引网交流侧产生电流间谐波。

②与Sab谐波分量相乘得到式(8)

cos{[nωm+mωc+ωh]t+nφm+mφc+φh}+

cos{[nωm+mωc-ωh]t+nφm+mφc-φh}

(8)

由式(8)可以看出，得到的牵引网电流中，除了高次谐波角频率nωm+mωc外，还产生了新的角频率nωm+mωc±ωh。同样，当ωh不是基波整数倍的角频率时，牵引网交流侧会产生电流间谐波。

实际运行中，由于牵引电机的复杂性，车载直流侧的纹波并非单一存在，经过整流器时会产生更多不同频率分布的间谐波，进而对整个牵引供电系统造成复杂的间谐波污染。

1.4.2 牵引网交流侧—车载直流侧间谐波模型

牵引网的电压.电流存在间谐波时，会在直流侧产生间谐波，同时也会对牵引网交流侧产生间谐波污染[18]。此处主要分析机车带来的间谐波影响，因此忽略背景间谐波的影响。

假设牵引网交流侧只存在基波分量和一个不同频率的间谐波，可得到如下关系

(9)

(10)

式中，kU为交流侧间谐波电压与基波电压的比值；kI为交流侧间谐波电流与基波电流Is的比值；ω为交流侧电压的角频率；ωh为交流侧间谐波电压的角频率；φ为交流侧电压和电流的夹角；φh为交流侧间谐波电压和间谐波电流的夹角。

牵引变流器输入功率Pin可表示为

Pin=usis=2UsIscosωtcos(ωt-φ)+

2kIUsIscosωtcos(ωht-φh)+

2kUUsIscosωhtcos(ωt-φ)+

2kUkIUsIscosωhtcos(ωht-φh)

(11)

由于牵引网间谐波含量的幅值相对于基波较小，因此可以忽略间谐波电压kUUs和间谐波电流kIIs的相互作用，则牵引变流器的输入功率可以简化为

Pin≈UsIscosφ+UsIscos(2ωt-φ)+

kIUsIscos[(ω+ωh)t-φh]+

kIUsIscos[(ω-ωh)t+φh]+

kUUsIscos[(ω+ωh)t-φ]+

kUUsIscos[(ω-ωh)t-φ]

(12)

由式(12)可以看出，牵引变流器的输入功率由稳态分量和动态分量2部分组成，其中直流分量UsIscosφ为稳态分量，其余各项间谐波分量为动态分量。

根据牵引变流器的等效数学模型可得输出功率Pout为

(13)

假设牵引变流器由理想开关器件组成，即在换相过程中不存在功率损失和能量储存，则根据能量守恒原理可得网侧瞬时输入功率和直流侧瞬时输出功率相等，则有

Pin=Pout

(14)

联立式(12)～式(14)，考虑输入输出功率对应的稳态分量和动态分量分别相等，可得

(15)

kIUsIscos[(ω+ωh)t-φh]+

kIUsIscos[(ω-ωh)t+φh]+

kUUsIscos[(ω+ωh)t-φ]+

kUUsIscos[(ω-ωh)t-φ]

(16)

(17)

由式(17)可以看出，当牵引网交流侧含有基波分量和一个不同频率的间谐波时，车载直流侧的纹波中除了产生二倍角频率的谐波外，同时还会产生角频率ω±ωh的间谐波。同理可推导，当牵引网交流侧含有谐波分量与多个不同频率的间谐波时，每个频率的间谐波都会在车载直流侧的纹波中围绕各个谐波频率正负叠加，从而产生大量的间谐波，造成间谐波污染。

1.4.3 车载直流侧与牵引网交流侧间谐波相互影响

1.4.1.1.4.2节分别分析了车载直流侧在牵引网交流侧产生的间谐波和牵引网交流侧在车载直流侧产生的间谐波，研究电力机车诱发的间谐波，必须考虑牵引网交流侧和车载直流侧之间的相互影响。

由于交流侧R和L不影响us与uab的间谐波分布，为了方便计算可将其省略。由于式(8)中is谐波附近间谐波含量较低，计算功率平衡中可以忽略。从车载直流侧出发，以直流侧单一纹波ωh为例，假设调制波的初相角φm=0，纹波电流的初相角φh=0，结合式(7).式(17)，经过n次迭代后，得到式(18)的直流侧电流间谐波表达式与式(19)的牵引网交流侧电流间谐波表达式。

(18)

cos[(2n+1)ω±ωh]t

(19)

通过上述分析发现，电力机车诱发的间谐波是车载直流侧和牵引网交流侧交替作用的结果。当车载直流侧存在纹波或者牵引网交流侧存在间谐波时，在整流器两侧的相互影响下，会交替产生更多的新频次的间谐波，从而造成整个频谱的间谐波污染。但是，无论直流侧向牵引网交流侧产生的间谐波，还是牵引网交流侧向直流侧产生的间谐波幅值均已很小，由其再次作用产生的间谐波可以忽略不计。因此不考虑间谐波的后续交替过程影响是合理的，对于牵引供电系统间谐波的分析可以主要考虑车载直流侧的初始纹波和牵引网交流侧的初始间谐波。

2 牵引供电系统联合仿真模型搭建

2.1 牵引网模型设置

牵引网是牵引供电系统的核心，其结构复杂，各导体之间存在电容耦合和互感。结合牵引网的空间分布和电气特性，考虑接触线.钢轨.正馈线和保护线之间的耦合关系，可搭建分布式参数的复线牵引网模型[19]，其主要线路参数如表2所示。

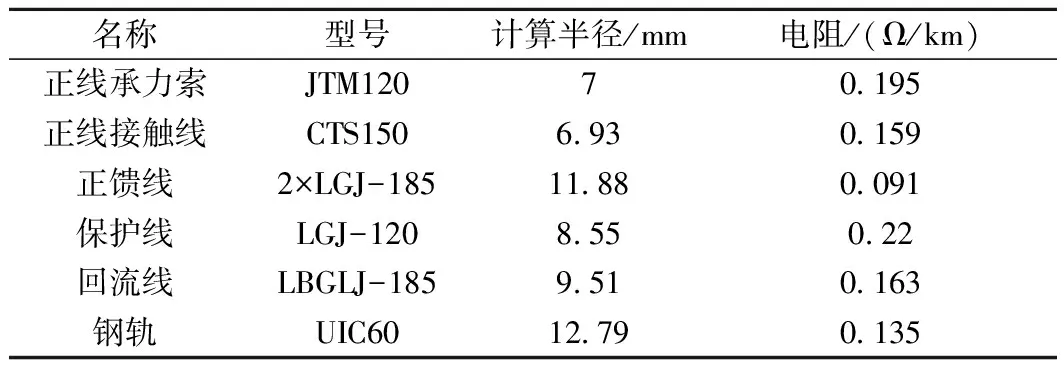
表2 牵引网线路参数

2.2 电力机车模型设置

电力机车是牵引供电系统谐波.间谐波的主要来源，其四象限变流器对机车的谐波.间谐波特性有决定性影响。以车载变压器为例，分析动车组的有功功率.无功功率.谐波特性等一般从机车的车载变压器低压侧开始。因此联合系统仿真中的机车模型可用四象限变流器代替，而机车变流器其他电气参数的变化受其自身闭环控制系统约束，可以视为用负荷代替的恒定负载。基于CRH3型电力机车的拓扑结构及工作原理，采用瞬态直流控制可搭建电力机车模型[2]，具体仿真参数如表3所示。

表3 CRH3型电力机车仿真参数

2.3 联合仿真模型

牵引变电所.牵引网和电力机车之间构成的回路是连续的，具有较强的耦合关系。结合上节仿真参数，基于PSCAD仿真软件，可建立如图5所示的高速铁路牵引供电系统联合仿真模型。

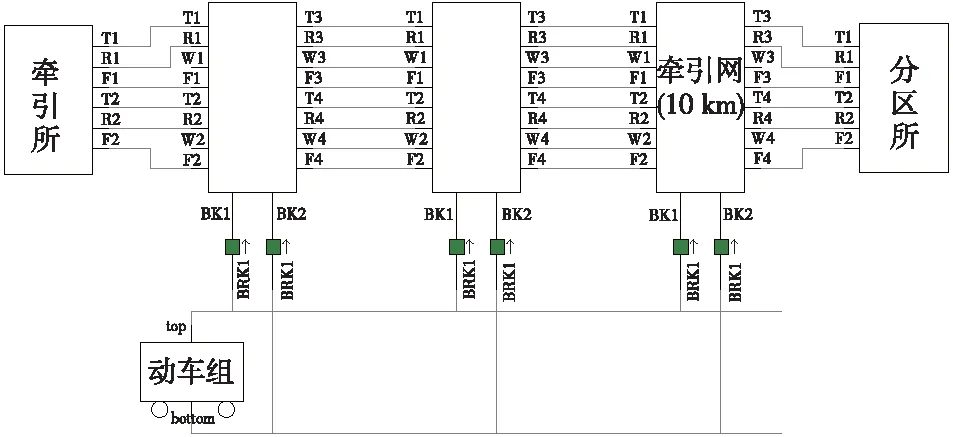
图5 高速铁路牵引供电系统联合仿真模型

由于PSCAD断路器在通断过程中不影响电感.电容元件的状态信息。在联合仿真模型中，将牵引网按每1 km一段进行离散化，通过控制每段断路器的通断，进而控制机车接入牵引网的位置，可以模拟移动运行的电力机车。

3 牵引供电系统间谐波阻抗特性

高速铁路牵引供电系统和外部电源的电气特性决定了其自身阻抗频率特性，基于间谐波电流注入法，对搭建的牵引网不同位置进行了间谐波阻抗的测量[20]，得到如图6.图7所示的间谐波幅频和相频曲线。

图6 间谐波幅频曲线

图7 间谐波相频曲线

在阻抗曲线中，990 Hz附近和2 870 Hz附近的阻抗幅值均达到极大值，阻抗相位均由+90°向-90°变化，表明在这2个频率附近会发生并联谐振。

根据现场测试中谐波统计信息，通常将牵引供电系统的谐波问题归为2类：一是谐振频率带(20～25倍基频)；二是特征频率带(45～55倍基频)。其中前者主要受系统自身阻抗参数影响，后者主要由动车组的四象限整流器的开关频率决定[2]。可将该高速铁路牵引供电系统模型的谐振频率进行如下划分：谐振频率带940～1 040 Hz，特征频率带2 770～2 970 Hz。

4 牵引供电系统间谐波传输特性

在PSCAD中，按照图5牵引供电系统联合仿真模型进行仿真，可得到典型的直流侧与交流侧电流波形。根据GB/T24337—2009《电能质量公共电网间谐波》给出的提取算法，将PSCAD生成的数据文件导入到Matlab中，并编写快速傅里叶变换(Fast Fourier Transform，FFT)频域特征提取算法程序可对电流进行间谐波频谱分析[21]。

4.1 车载直流侧间谐波含量与分析

直流侧接入电阻负载，其电压电流趋势一致，间谐波含量相同，典型的直流侧的电流波形如图8所示，可以看出，直流侧电流经过0.5 s后稳定在30 A左右，仿真结果稳定。

图8 直流侧电流波形

直流侧电流间谐波频谱如图9所示，该图表示的是各频次间谐波幅值与直流分量的比值。由于变流器的载波频率为350 Hz，其在直流侧产生的间谐波分布较少，主要分布在0～350 Hz区间，其中0 Hz附近间谐波含量较为丰富，但随着频率的增加，间谐波含量逐渐减小。表4给出了直流侧电流间谐波的分布情况，最高间谐波含量为2.87%。

图9 直流侧电流间谐波频谱

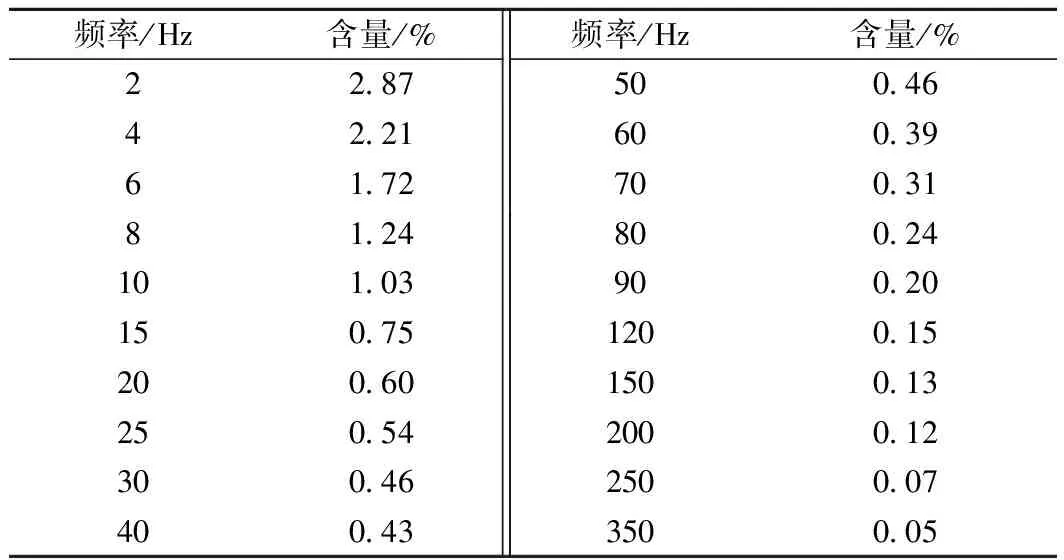
表4 直流侧电流间谐波分布

4.2 牵引网交流侧间谐波含量与分析

根据GB/T24337—2009《电能质量公共电网间谐波》规定，100 Hz以下间谐波含有率限值0.16%，100～800 Hz间谐波含有率限值0.4%，800 Hz以上的间谐波限值还在研究中。

典型的交流侧电流波形如图10所示，可以看出，交流侧电流的波形存在畸变，说明其内部含有谐波与间谐波。图11给出了交流侧全频段电流间谐波分量与基波分量的比值，可以看出交流侧电压间谐波主要存在于基频.谐振频率带和特征频率带附近，如图中虚线所示。这是由于在交流侧基频占据主导，谐振频率带与特征频率带谐波含量相对其他频率更高，因此间谐波存在的主要范围也在这3种频率附近。

图10 交流侧电流波形

图11 交流侧电流间谐波频谱

由前述分析可知，直流侧产生的间谐波会在交流侧沿基频和基频的整数倍展开，表5和表6分别给出了电力机车在不同工况.不同位置时，变流器交流侧与电源侧电流间谐波的峰值分布情况。可以发现间谐波分布特点。

表5 变流器交流侧电流间谐波峰值含量 %

表6 电源侧电流间谐波峰值含量 %

(1)同一工况下，不同位置处的间谐波含量相近。

(2)同一位置处，牵引工况较制动工况间谐波含量的峰值更高，间谐波含量更为丰富。

(3)变流器交流侧间谐波含量丰富，基频附近电流间谐波最高可达39.72%，超过规定含量0.16%，存在严重超标；谐振频率带附近电流间谐波最高可达1.84%，超过规定含量0.4%，存在超标；特征频率带附近电流间谐波最高可达0.53%，由于没有相关限值规定，有可能存在一定超标情况。

(4)电源侧间谐波含量主要集中在基频附近，其电流间谐波最高可达5.53%，超过规定含量0.16%，存在超标情况。

5 结论

(1)高速铁路牵引供电系统的间谐波来源分为4个部分：电力系统背景间谐波；铁磁元件非线性特性诱发间谐波；牵引网并联谐振诱发间谐波；电力机车诱发间谐波。

(2)在特定条件下，仿真计算显示高速铁路牵引供电系统电源侧间谐波主要集中在基频附近，其电流间谐波含量最高可达5.53%，超过国家标准规定的0.16%，存在超标情况。

(3)间谐波会造成高速铁路供电电能质量的下降，甚至引发间谐波谐振，对设备的绝缘造成影响，在设计和运行维护时，应当给予高度重视。