基于经验模态分解谱峭度重构峰值定位的电机噪声溯源方法*

冯爽 许琦 罗园庆 陈长征

（沈阳工业大学，沈阳 110870）

主题词：无刷直流电机 经验模态分解谱峭度重构 噪声溯源

1 前言

噪声溯源是对电机进行针对性降噪的前提。近年来，国内外许多学者对电机噪声的分离与识别进行了相关研究。于莫岩等[1]基于阶次分析法对永磁同步电机的电磁力激励特征和滚动轴承噪声阶次进行分析，对电机的噪声源进行识别。吴双龙等[2]对爪极电机的机械噪声、气动噪声和电磁噪声进行分析，利用阶次分析方法对电机噪声进行识别与定位。Huang等[3]基于噪声的传递路径建立激励源的振动传递模型，解释了不同负载下电机内部噪声源及主要噪声的传递规律。Cho[4]基于近场声压测量结果，根据声全息理论重建电机的粒子速度，结合冲击条件下静止电机的粒子速度和多转速电机噪声对电机进行声源定位。朱标等[5]使用声学刷技术对空调进行声全息分析，确定了对空调噪声贡献最大的位置。Cao等[6]对电机的振动和噪声信号进行测量并进行功率谱分析，探究了引起振动和噪声的原因，从而实现噪声源定位。

综合上述噪声源识别方法，在电机运行过程中测得的振动噪声信号成分驳杂：在进行传统的频谱分析时，噪声信号的频谱上会产生明显的“频率模糊”；声全息法虽然能很好地识别噪声源所在位置，但针对特定对象进行分析时，不能明确地找到产生噪声的具体原因，且依赖声全息设备；阶次分析法在电机噪声识别时对信号的信噪比要求较高，容易受到其他信号的干扰。

针对上述问题，本文提出一种基于经验模态分解谱峭度重构峰值定位（Empirical Mode Decomposition spectral Kurtosis Reconstruction Find Peaks，EMD-KRFP）的声溯源方法，按照阶次分析法的思路，首先对电磁力、转矩脉动和共振引起的噪声频率进行计算并定义为特征频率集，随后对采集到的噪声信号进行经验模态分解（Empirical Mode Decomposition，EMD），得到多个本征模态函数（Intrinsic Mode Function，IMF）分量并根据谱峭度理论对IMF进行筛选与重构，然后对重构信号进行快速傅里叶变换并使用峰值定位算法提取峰值频率，最后将提取到的峰值频率与计算得到的噪声特征频率集对照，得到噪声产生的原因。

2 经验模态分解谱峭度重构峰值定位理论

EMD-KR-FP是在经验模态分解的基础上，根据谱峭度进行信号重构，采用峰值定位进行噪声溯源的方法。

EMD算法假设任何信号都是由若干个有限的本征模态函数和无用噪声组成[7]，原信号的表达式为：

式中，ci(t)为第i个本征模态分量；n为本征模态分量数量；rn(t)为信号无用部分。

引入谱峭度理论[8]对信号进行分析。峭度是对波形的尖峰程度进行描述的无量纲参数，在噪声干扰较小的状态监测中，可利用其对奇异信号的敏感性来检测系统的异常响应。峭度K可定义为：

式中，μ、σ分别为信号x的均差与标准差；E(x-μ)为(x-μ)的期望值。

谱峭度的能量归一化累积量，即概率密度函数H的峰值度量为：

式中，S2Y(f)为2阶瞬时矩，是复包络能量的度量；S4Y(f)为4阶瞬时矩；C4Y(f)为四阶谱峭度。

根据谱峭度的关系，选择合适的峭度系数，对经验模态分解后的IMF分量进行筛选并重构，得到重构的信号的时域波形图。在此基础上对滤波后的信号进行傅里叶变换，并对其进行峰值频率定位。

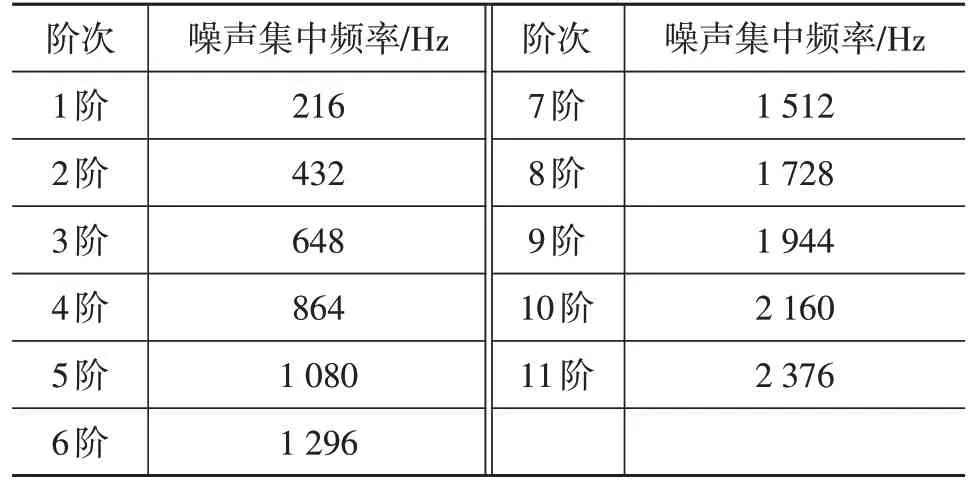
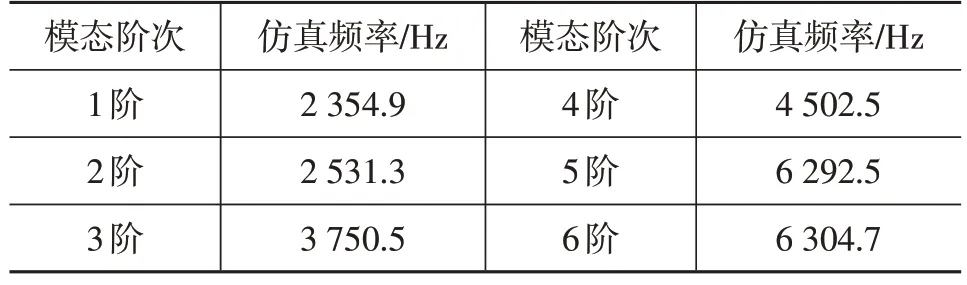
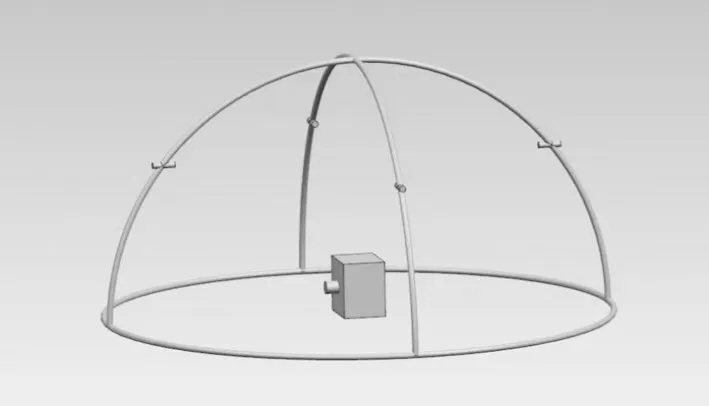
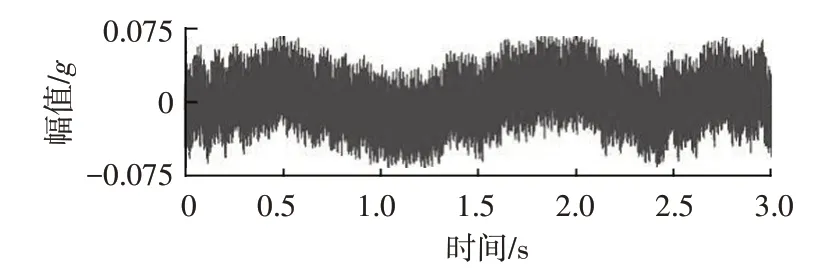
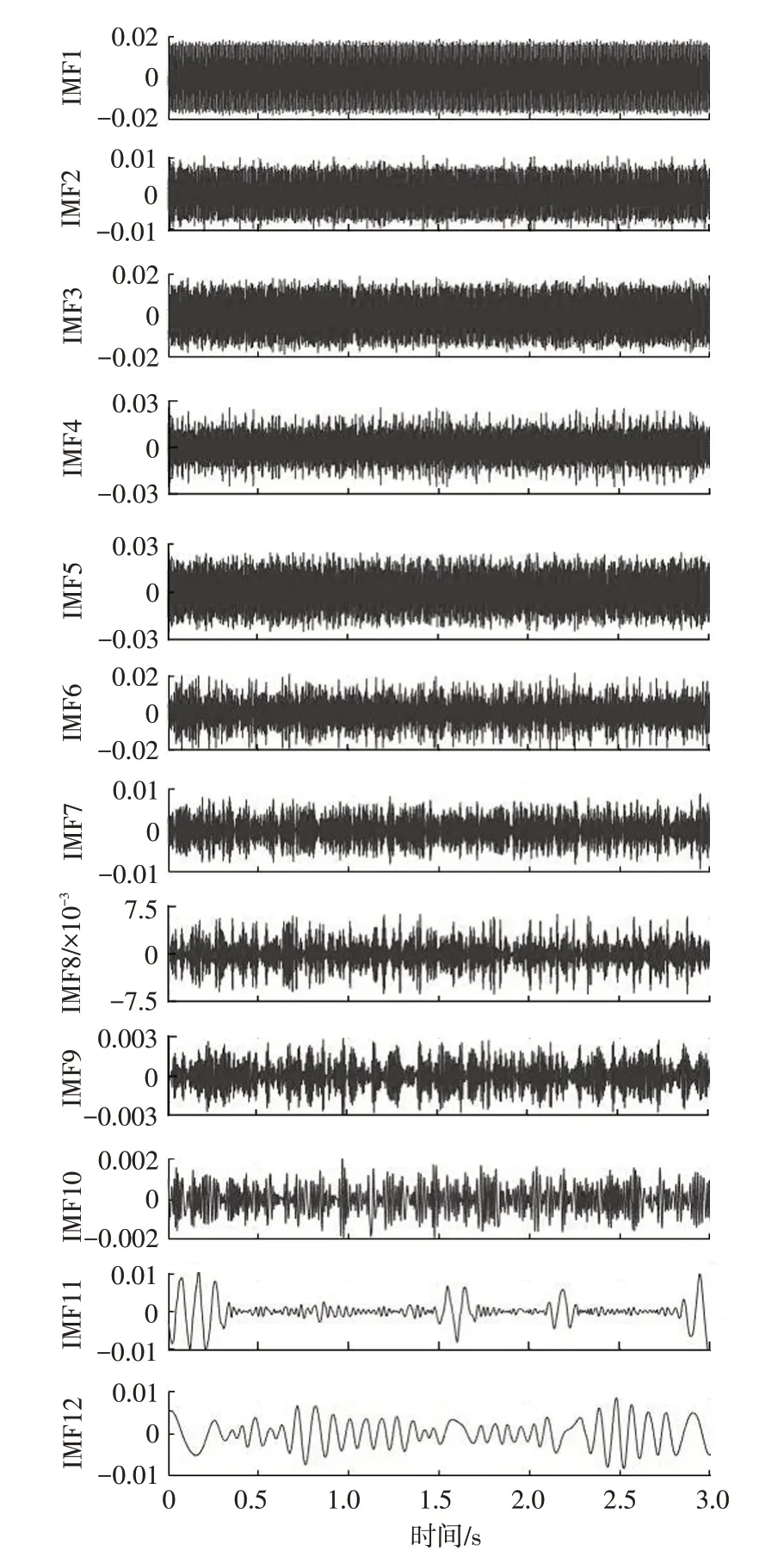
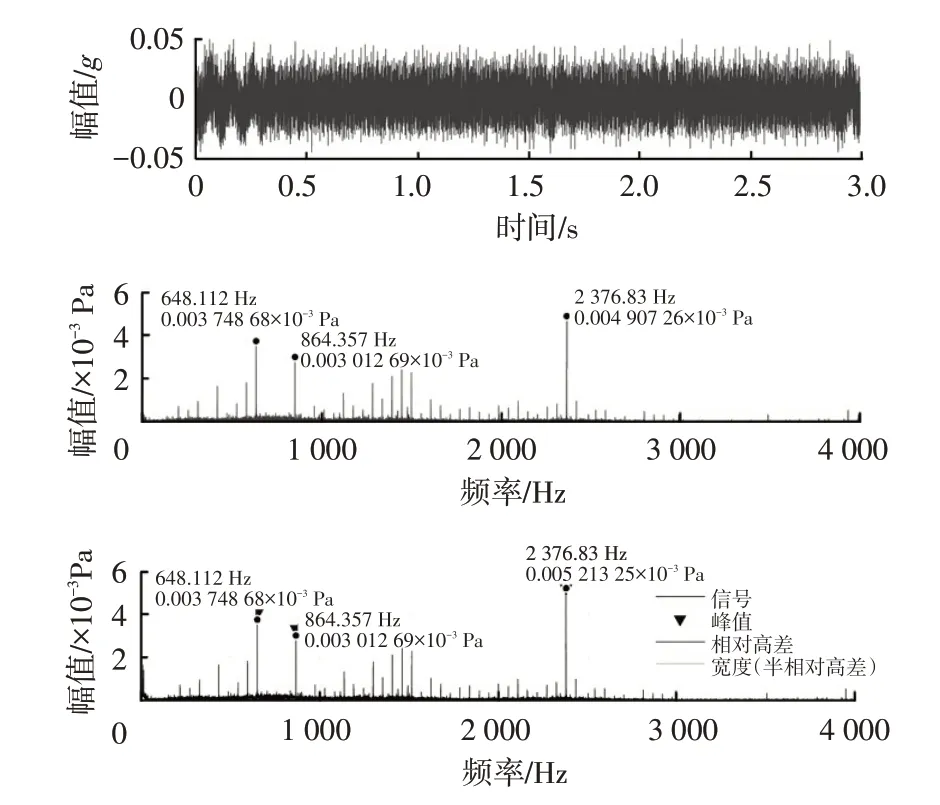
将试验测得的声音信号定义为2组列向量，分别为频率向量x(i)和幅值向量y(j)。将y(j)与其相邻2 个幅值进行对比，若y(j-1)

但在大多数情况下，若只采用y(i)与其相邻2 个幅值进行对比，在非意向区域也会取得峰值点，但峰值点的幅值对整体分析意义不大，此时需定义峰值点幅值的取值范围，尽可能提取对信号整体贡献较大的峰值点。

确定峰值点幅值取值范围后，信号频谱上仍存在曲线不光滑的问题，通常每个波峰附近都存在若干个谐波小波峰，导致提取的峰值与频率数量过多，影响后续的计算。故需对提取的每个峰值点定义峰值带宽。峰值提取流程如下：

a.从0 Hz 开始，定义第1 个带宽W(1)，在W(1)内比较提取的所有峰值点的幅值，取最大的峰值点Y(1)。

b.再将W(1)取得的最大峰值点设置为频带W(2)的中心，提取W(2)中所有峰值进行对比，得到最大峰值点Y(2)。

c.若Y(2)=Y(1)，则取得峰值点为附近带宽内最大的峰值点，定义为Z(1)并存储，同时以W(2)的末尾为下一频带W(3)的起点，继续进行迭代计算。

d.若Y(2)>Y(1)，则将Y(2)设置为频带W(3)的中心，再次进行步骤b的操作并进行判定，直至得到Y(k+1)=Y(k)。

3 电机噪声特征频率计算

3.1 径向电磁力引起噪声的特征频率计算

测试样机为4 极15 槽无刷直流电机，试验转速为3 240 r/min。

根据麦克斯韦张量方程，作用于定子齿表面的径向电磁力可表示为[9]：

式中，brs为径向气隙磁通量密度；bts为切向磁通密度；μ0为真空磁导率。

当电机槽口为开口槽时，不能忽略切向气隙磁通密度对径向力的贡献，而对于常见的半闭口槽电机，切向磁通量密度相对于径向磁通量密度小得多，因此在推导径向电磁力时，忽略切向磁通量密度的影响，则式（4）可简化为：

在旋转机械中，常采用频率阶次表示激励频率与转频基频fr间的倍数关系。本文电机转速为3 240 r/min，故取fr=54 Hz，由电机电磁噪声机理可知，理想条件下电机径向电磁力波的特征频率f为：

式中，k为径向电磁力阶次；p为电机极对数，本文采用4极15槽电机，故取p=2。

电磁力引起的噪声集中频率与径向力频率相同，故由电磁力引起的噪声集中频率如表1所示。

表1 定子表面径向电磁力引起的噪声集中频率

3.2 定子与径向电磁力共振引起的噪声特征频率计算

对电机进行模态仿真，采用自由模态的计算方式对电机的定子铁芯进行有限元仿真，由于电机的电磁力主要作用在电机定子的径向方向[10]，所以在仿真过程中着重计算径向模态振型，结果如图1示。

图1 前6阶自由模态

根据仿真结果，得到电机的各阶模态的频率，如表2所示。

表2 定子前6阶自由模态

由于电磁力与电机定子共振主要发生在定子的1 阶固有频率处，电机的第11 阶径向电磁力频率为2 376 Hz，处于定子固有频率附近，故推断电机共振频率在2 376 Hz 左右。

3.3 转矩脉动引起的噪声特征频率计算

在电机的换相过程中，电机绕组呈感性且电机的供电电源为有限容量电压源，故换相绕组上的相电流变化不会在瞬间完成。

而电机换相电流引起的转矩脉动的频率表达式为：

式中，l=1,2,3…；m为电机相数。

所以，电机的转矩脉动引起的噪声频率应主要集中在324 Hz、648 Hz、972 Hz、1 296 Hz。

4 电机噪声信号的采集

4.1 信号采集环境及设备

测试环境为半消声室，如图2 所示，信号采集所需设备和测试系统如表3所示。

图2 半消声室

表3 信号采集设备及测试系统

4.2 信号采集方法

根据GB 10069.1—2006《旋转电机噪声测定方法及限值》[11]中的测试要求，由于试验电机的轴心高度小于90 mm，所以电机噪声测试采用半球面测试，如图3 示，测试半径为400 mm，4 个测点分别位于电机前、后、左、右4个相互垂直的方向上，测点高度为250 mm，测试球面的中心为通过电机中心的垂线与地面的交点。电机转速为3 240 r/min，采样频率设置为12 800 Hz。电机实测场景如图4示，信号采集界面如图5示。

图3 噪声测试示意

图4 电机实测场景

图5 号采集界面

5 电机噪声信号处理

对试验信号进行处理的流程如下：

a.采用EMD 算法对电机的声音信号进行分解，比对得到的各IMF 与原始信号的相关系数并计算各IMF的峭度。

b.取相关系数较大，且超过峭度阈值的IMF分量进行信号重构，对重构的信号进行快速傅里叶变换，得到重构信号的频谱图。

c.使用寻峰函数提取新信号的峰值频率，与前文定义的电机噪声特征频率进行对照，得到该电机噪声产生的主要原因。

试验采集的原噪声信号时域波形如图6示。

图6 原始信号时域波形

对原噪声信号进行经验模态分解，取前12 个IMF分量，如图7示。

图7 IMF分量

由谱峭度理论，对峭度超过2.5的信号进行重构，并进行快速傅里叶变换，提取对噪声贡献最大的3个峰值频率，结果如图8示。

图8 信号处理后结果

由图8可知，对电机噪声信号进行滤波处理后噪声信号变得更为干净，峰值明显，对电机噪声贡献最大的3个峰值频率分别为648.112 Hz、864.357 Hz、2 376.83 Hz。与测试样机噪声特征频率集对照后得到结果为：引起648.112 Hz 处电机噪声的主要原因是转矩脉动；引起864.357 Hz处电机噪声的主要原因是电机径向电磁力；引起2 376.83 Hz处电机噪声的主要原因是电机的第11阶径向电磁力与电机定子共振。

6 结束语

本文采用EMD-KR-FP 算法对电机的噪声信号进行分解并根据谱峭度理论对信号进行重构，对重构信号进行快速傅里叶变换得到新信号的频谱图进行峰值频率定位，选取贡献最大的3 个峰值，与电机噪声特征频率集进行对照，从而确定引起电机噪声的主要原因。

本文提出的EMD-KR-FP 电机噪声溯源方法在阶次分析法的基础上，运用算法对电机噪声信号进行处理以及噪声源定位，经试验验证有效，相比于传统的电机噪声分析法，该方法减少了人工分析频谱的环节，降低了电机电磁噪声分析过程的工作量。