车辆与电网互动模式下电动汽车充放电控制策略研究

王涛 郑阔 刘旺磊

（河北工程大学，邯郸 056038）

主题词：车辆与电网互动 电动汽车 双向AC/DC变换器 充放电控制策略空间矢量脉冲宽度调制

1 前言

电动汽车（Electric Vehicle，EV）是一种新型动态高能量负荷，其大规模无序入网将给电网的负荷平衡带来新的挑战[1-2]。电动汽车既是能量负荷单元，也是能量存储单元，具有荷-源双重复合性，作为动态分布式能量存储单元参与车辆与电网互动（Vehicle to Grid，V2G）服务，能够平抑峰谷负荷差，快速响应电网的调峰调频命令，最优化电网运行能力[3-5]。

V2G 的关键在于双向变换器的设计。文献[6]提出了双向H 桥DC/DC 变换器，相比于普通的双向半桥DC/DC变换器，具有可在不同电压等级下工作且输出电压范围宽的优点。文献[7]提出了一种零电压转换三电平双向DC/DC 变换器，可在更高的开关频率下工作，实现更高的功率密度和效率。文献[8]提出了一种电压型双有源桥型（Dual Active Bridge，DAB）双向DC/DC 变换器拓扑结构，采用相移调制技术进行功率流控制，具有电气隔离、软开关和优越的双向潮流能力等优点，但其电压转换范围较小，且会给系统注入较大的无功功率。文献[9]提出的T 型三电平逆变器可实现能量的双向流动，但其功率开关管数量多，控制结构复杂，在应用中存在中点电位不平衡问题。

相比于单级式双向AC/DC 变换器，两级式双向AC/DC变换器拓宽了输出电压范围，可有效调节蓄电池的充放电过程，延长蓄电池的使用周期。本文以两级式双向AC/DC变换器为研究对象，针对电动汽车的荷-源双重复合性设计前馈解耦电压电流双闭环控制策略，对双闭环的PI 参数进行整定并根据伯德（Bode）图分析系统的稳定性，采用恒流充放电控制策略控制功率流的双向流动，并针对高频谐波抑制问题，设计无源阻尼型LCL滤波器。最后，在MATLAB/Simulink中搭建系统仿真模型，仿真分析所提出的控制策略的可行性与有效性。

2 V2G充电桩数学模型建立

本文采用无隔离两级式双向AC/DC 变换器，由三相电压型脉冲宽度调制（Pulse Width Modulation，PWM）变换器和双向DC/DC 变换器构成主电路拓扑结构，如图1 所示。在用电低谷期，电动汽车作为负荷接入电网，三相电压型PWM 变换器工作在整流状态从电网中吸收能量，经过双向DC/DC 变换器降压进行充电，网侧电压电流同相位；在用电高峰期，电动汽车作为临时电源接入电网反馈能量，三相电压型PWM 变换器工作在有源逆变状态，双向DC/DC 变换器工作在升压状态，网侧电压电流相位相差180°。

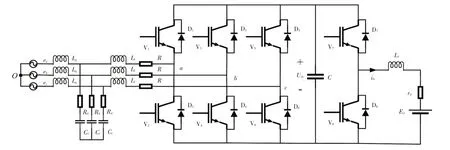
图1 V2G模式主电路拓扑结构

2.1 三相电压型PWM变换器

三相电压型PWM变换器由3个单向半桥逆变电路组成，同一桥臂的上、下2个半桥工作状态互补，能量双向流动的功能通过电流方向的改变实现，采用空间矢量脉冲宽度调制（Space Vector Pulse Width Modulation，SVPWM）技术生成功率开关管V1～V6的开关信号。

根据图1，在低频状态下将LCL 型滤波器等效为L型滤波器进行设计，应用基尔霍夫定律，建立在三相静止坐标系下的数学模型：

式中，ea、eb、ec分别为电网a、b、c相电压；ia、ib、ic分别为网侧a、b、c相电流；ua、ub、uc分别为整流器输入端与中性点O之间的a、b、c相电压；R为等效电阻；L=Lf+Lg为总电感；Lf、Lg分别为桥臂侧电感和网侧电感。

在三相静止坐标系下，交流侧电压与电流无耦合关系，但电压和电流是时刻变化的。为便于设计PI 控制器，实现无静差控制，必须经过克拉克（Clark）变换和派克（Park）变换将三相静止坐标系下的交流量转化为d-q旋转坐标系下的直流量[10]。

将式（1）经过Clark 变换转化到α-β两相静止坐标系下，变换关系式为：

式中，xα、xβ分别为相应物理量的α、β轴分量；xa、xb、xc分别为相应物理量的a、b、c相分量。

联立式（1）、式（2）可得α-β坐标系下的数学模型：

式中，iα、iβ分别为网侧电流的α、β轴分量；eα、eβ分别为网侧电压的α、β轴分量；uα、uβ分别为变换器交流侧电压的α、β轴分量。

将式（3）经过Park 变换转化到d-q旋转坐标系下，变换关系式为：

式中，xd、xq分别为相应物理量的d、q轴分量；ω为d-q轴旋转角速度；t为时间。

联立式（3）、式（4）可得d-q坐标系下数学模型：

式中，id、iq分别为网侧电流的d、q轴分量；ed、eq分别为网侧电压的d、q轴分量；ud、uq分别为变换器交流侧电压的d、q轴分量。

2.2 双向DC/DC变换器

双向DC/DC 变换器选择Buck/Boost 拓扑结构实现升压和降压2 种状态。功率开关管V7、V8不能同时导通，通过正弦脉宽调制技术产生V7、V8的驱动脉冲，改变占空比可调整输出电压。

2.2.1 蓄电池充电降压

充电时双向DC/DC变换器等效为V7和D8构成的降压斩波（Buck）电路，V7导通时，D8截止，充电电流i0按指数曲线上升，基于分时段线性电路思想[11]，由基尔霍夫定律可得：

式中，Udc为直流母线电压；i0为充电电流；Ed为蓄电池等效电动势；rd为蓄电池等效电阻；L1为直流侧电感。

根据式（6），由三要素法可解得i0，当V7截止时，i0达到电流最大值I20，则：

式中，τ=L/R为时间常数；I10为V7导通时的电流初值；ton为开关管的通态时间。

当V7处于断态时，D8导通续流时的初值为电流最大值I20，电感L1作为储能元件与蓄电池构成回路释放能量，i0呈指数曲线下降，则：

根据式（8），由三要素法可解得i0，当D8截止时，i0等于V7导通初态的电流初值I10，则：

式中，toff为开关管的断态时间。

联立式（7）、式（9）可解得：

式中，T=ton+toff为开关周期；α为占空比。

由ton/T≤1 可判断此时为降压工作状态，即充电过程。

2.2.2 蓄电池放电升压

放电时，双向DC/DC 变换器等效为V8和D7构成升压斩波（Boost）电路，基于分时段线性电路思想，与Buck电路类似的方法可解得：

由T/toff≥1 可判断此时为升压工作状态，即放电过程。

3 电动汽车充放电控制策略研究

3.1 前馈解耦控制

分析式（5）可知，d-q轴之间存在2 个耦合项，为得到独立的直流变量id和iq并进行单独控制，采用PI控制器解耦，控制框图如图2所示，则：

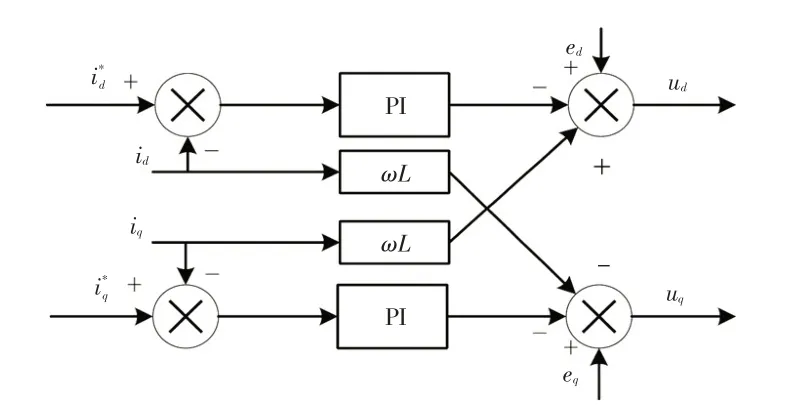
图2 前馈解耦控制框图

式中，Kip、KiI分别为电流环比例系数、积分系数；、分别为d、q轴电流指令值。

联立式（5）、式（12）可解得前馈解耦后的数学模型：

式中，s为复频率。

由式（13）可知，2 个耦合项被消除，电网电压前馈解耦的电流回路控制框图如图3所示。、分别控制系统的有功功率和无功功率，系统以单位功率因数运行，故令=0。

图3 电网电压前馈解耦的电流回路控制框图

3.2 双闭环PI控制器设计

采用电压、电流双闭环控制策略，电流内环使控制过程的动态响应速度更快，电压外环可增强控制系统的抗干扰能力。电流内环的控制指令由电压外环提供，将直流母线电压Udc与电压参考值相减，经过PI控制器得到d轴电流内环指令值，电流内环输出项与电流前馈解耦项和电压前馈补偿项叠加后输出d-q旋转坐标系下交流侧电压参考值ud与uq，经过d-q两相旋转坐标系到α-β两相静止坐标系的变换后，由SVPWM 技术得到功率开关器件V1～V6的驱动信号。

3.2.1 电流内环控制系统设计

图4所示为电流内环控制结构简化框图，其中1.5Ts合并了采样延迟环节的时间常数Ts和小惯性环节的时间常数0.5Ts。

图4 电流内环控制结构简化框图

令电流环时间常数τi=Kip/KiI=L/R，加入补偿环节后的开环传递函数为：

式中，Ts为开关周期；Kpwm为等效增益，采用SVPWM 调制时为1。

按照典型Ⅰ型系统进行参数整定，取阻尼比ξ=0.707，则：

由式（15）计算可得PI参数：

计算可得：Kip≈16.7，KiI≈226.7。

合并时间常数Ts与0.5Ts前、后的幅频与相频特性曲线如图5所示，在中低频段，2条曲线基本重合。合并前截止频率为4 310 rad/s、相角裕度为63.2°，合并后截止频率为4 090 rad/s、相角裕度为65.2°，对系统稳定性和带宽影响较小。

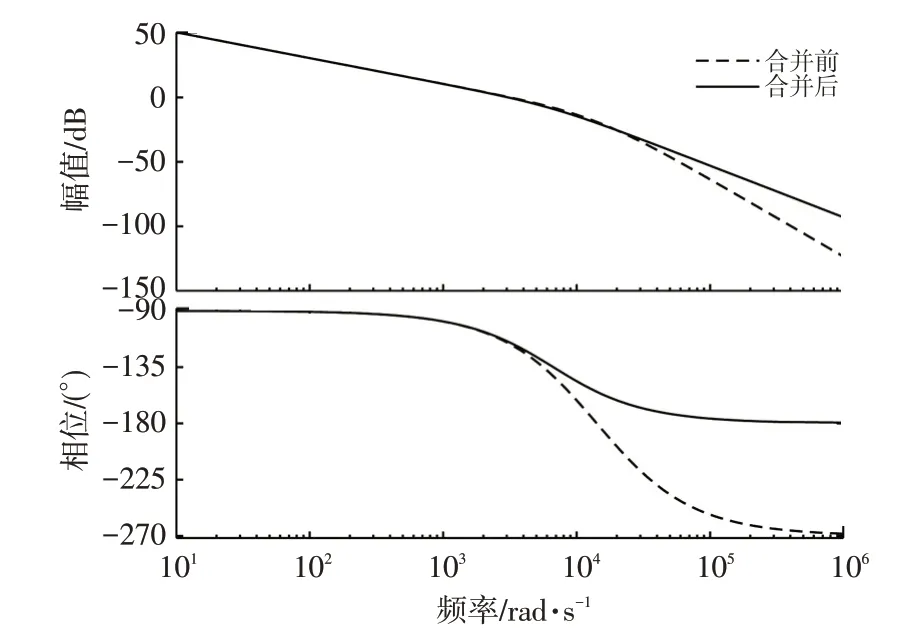
图5 电流内环Bode图

电流内环作为电压外环的传递函数，开关周期Ts很小，可忽略s2项，则电流内环闭环传递函数为：

3.2.2 电压外环控制系统设计

图6所示为电压外环控制结构简化框图，其中Tev表示合并电流闭环传递函数等效为一阶惯性环节的时间常数3Ts和采样小惯性环节的时间常数Tv，即Tev=3Ts+Tv。开关频率fsw远大于基波频率，只考虑开关函数的低频分量[12]，时间变量K=0.75mcosθ≤1，其中m≤1 为PWM 调制比，θ为初始相位角度，K受θ影响，为时变量，故用最大增益0.75代替K。

图6 电压外环控制结构简化框图

则电压外环开环传递函数为：

式中，τv为电压外环时间常数；Kvp电压环比例系数；C为直流侧电容。

电压外环按照典型Ⅱ型系统进行参数整定，取中频带宽hv=τv/Tev=5，则：

式中，hv为中频带宽。

由式（19）计算可得PI参数：

式中，KvI为电压环积分系数。

计算可得Kvp=10，KvI=5 000。

合并时间常数3Ts与Tv前、后的幅频与相频特性曲线如图7所示，在中低频段，2条曲线基本重合。合并前截止频率为1 900 rad/s、相角裕度为47.5°，合并后截止频率为1 790 rad/s、相角裕度为41.1°，系统具有较好的稳定裕度和带宽。

图7 电压外环Bode图

分析图5、图7可知，内、外环截止频率相差过小，故电压外环PI参数还需通过仿真再次整定。

3.3 双向DC/DC变换器控制策略

3.3.1 恒流充放电控制策略

恒流充放电控制框图如图8所示，双向DC/DC变换器采用恒流充放电控制策略，充放电共用同一个单电流闭环PI 控制器。计算额定充放电电流与实际电流i0的误差，经PI 控制器限幅后与三角载波比较输出功率开关管V7、V8的PWM信号。

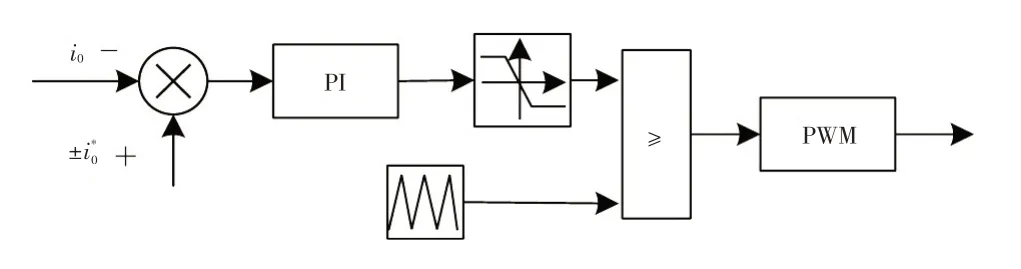
图8 恒流充放电控制框图

3.3.2 直流侧参数设计

直流侧电容可稳定整流器输出电压，缓冲交直流的能量转换，则：

式中，ΔUmax为直流侧电压波动，取直流母线电压的5%；tr为上升时间；Rdc为等效电阻；P为额定总功率。

直流侧电感需同时满足Buck 和Boost 2 种工作模式，则：

式中，ΔIr为纹波电流，取充电电流的3%；fsw=10 kHz为开关频率；Ud为蓄电池端电压。

计算得122 μ F≤C≤6 210 μ F、L1≈19 mH，取C=5 000 μ F、L1=20 mH。

4 LCL滤波器设计

电动汽车属于非线性负荷，并入电网会产生大量高次谐波，因此必须对并网电流进行滤波，使其满足并网电流谐波总畸变率（Total Harmonic Distortion，THD）≤5%的要求。LCL滤波器在高频段以-60 dB/dec衰减，电容元件支路的容抗Xc=1/ωC与频率f成反比，对高频分量呈现低阻抗作用并提供通路分流，从而可抑制高频谐波电流流入电网[13]。而电感支路的感抗XL=ωL与频率f成正比，对高频谐波分量呈现高阻抗作用，因而LCL 滤波器具有良好的高频衰减特性，故本文选择LCL滤波器进行设计，LCL滤波器如图9所示。

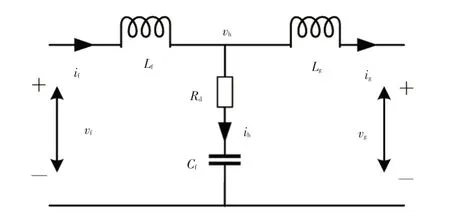
图9 LCL滤波器

4.1 LCL滤波器数学模型

由单相LCL滤波器推广到三相LCL滤波器中，根据图9 应用基尔霍夫定律推导数学模型并绘制等效框图如图10所示，则：

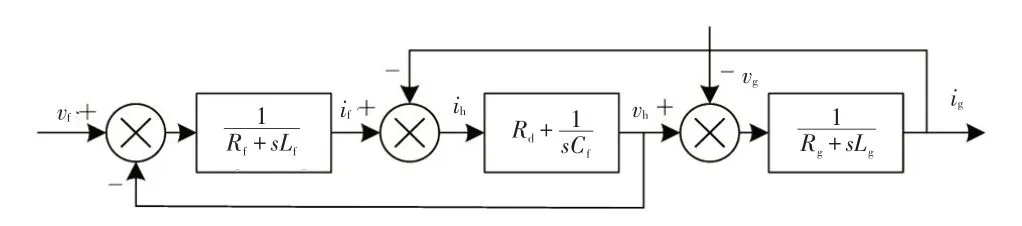
图10 LCL滤波器等效框图

式中，Rf、Rg分别为电感Lf和Lg的寄生电阻；Rd为阻尼电阻；Cf为滤波电容；ih、if、ig分别为流过Cf、Lf和Lg的电流；vf、vg、vh分别为桥臂侧、网侧和电容支路电压。

忽略寄生电阻Rf和Rg，根据图10，由梅逊公式可得桥臂侧电压vf与网侧电流ig的传递函数：

由式（24）可知，LCL 滤波器是三阶系统，具有良好的高频衰减特性，但在谐振频率处有谐振尖峰，故本文采用无源阻尼法抑制谐振尖峰。

4.2 LCL滤波器参数设计

电容越大，LCL 滤波器对高频谐波的抑制效果越好，但系统无功损耗增大，功率因数降低，则：

式中，E为网侧电压有效值。

电感增大会导致无功损耗增大，其体积和压降损耗均会增加，且动态响应变差，则：

式中，Em、Im分别为网侧电压和电流最大值。

约束Lf≥Lg，Lg=rLf，取r=0.3。并网电流纹波大小取决于Lf，则：

式中，ΔImax为电流纹波，取额定电流的20%。

LCL滤波器在谐振频率fres处电流谐波较大，因此fres需满足，基波频率fn=50 Hz，计算可得0.05 kHz＜fres=1 670 Hz＜5 kHz。采用滤波电容串联阻尼电阻Rd的无源阻尼法抑制谐振尖峰，但阻尼电阻过大会引起功率损耗[14]，则：

式中，ωres=1/fres为谐振角频率。

计算可得Cf≤16.4 μF、Lf+Lg≤9.2 mH、Lf≥3.8 mH、Rd≤3.1 Ω，取Cf=10 μF、Lf=3.8 mH、Rd=2.5 Ω。

5 系统仿真及分析

在MATLAB/Simulink 中搭建V2G 模式下电动汽车充放电的仿真模型，如图11 所示。仿真中加入锁相环模块，其作用是锁定电网相位信息，提供参考角频率。为实现单位功率因数充放电，即控制无功功率Q=0，故设定q轴电流指令值=0。

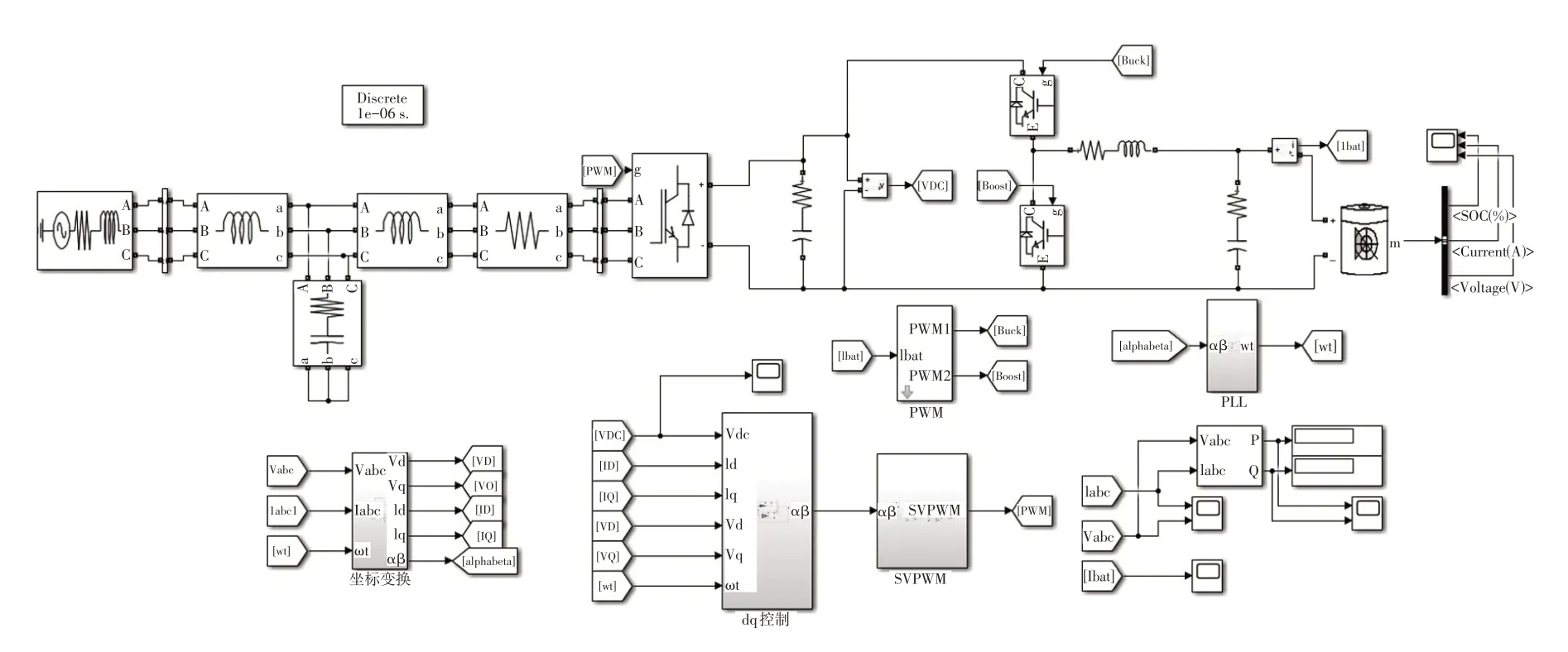
图11 V2G仿真模型原理图

网侧电压电流波形如图12所示，规定在V2G模式下充电电流方向为正，网侧电压和电流波形均为正弦波且无明显畸变，没有较大的冲击电流，充电时网侧电压、电流波形相位相同，放电时网侧电压、电流相位相差180°。

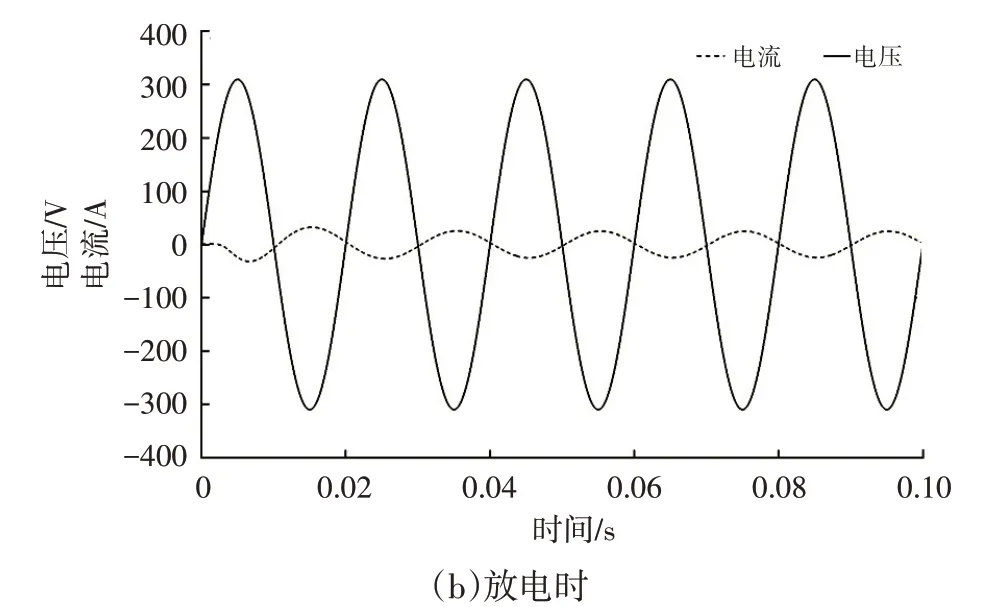
图12 网侧电压电流波形

恒流充放电时电流波形如图13 所示，由图13 可知：电动汽车充放电电流较快稳定在±30 A 左右；充电时电流波形经过约0.012 s 逐渐上升至30 A 且无超调，随后一直保持稳定；在放电初始阶段，电流波形出现波形超调现象，经过约0.018 s短暂调节后保持稳定。

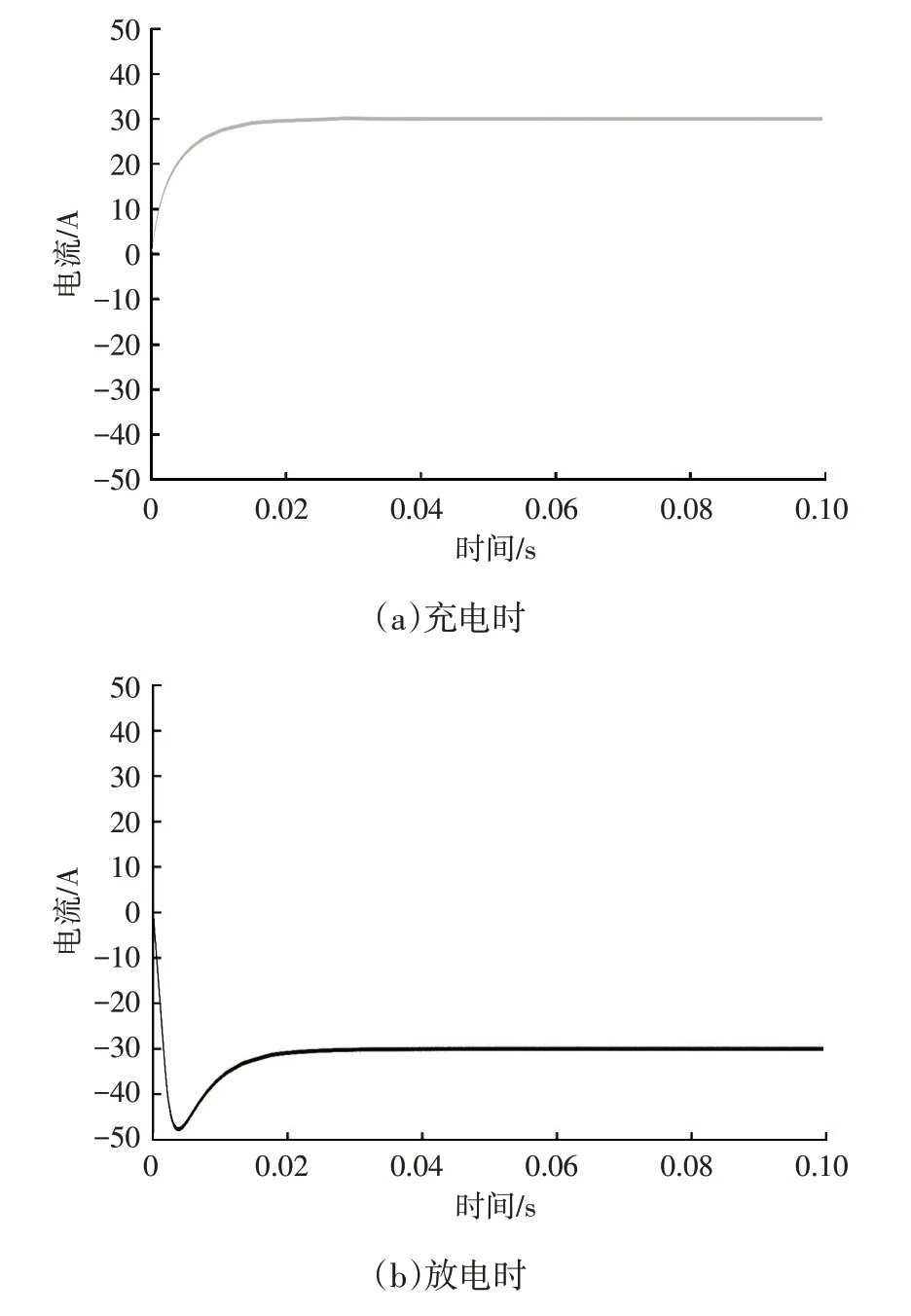
图13 恒流充放电时电流波形

充放电时直流母线电压波形如图14 所示，由图14可知：充电初始阶段直流母线电压Udc<，系统工作在整流和降压状态；放电初始阶段Udc>，系统工作在逆变和升压状态；直流侧母线电压最终稳定在700 V左右，调节时间短且超调量小。

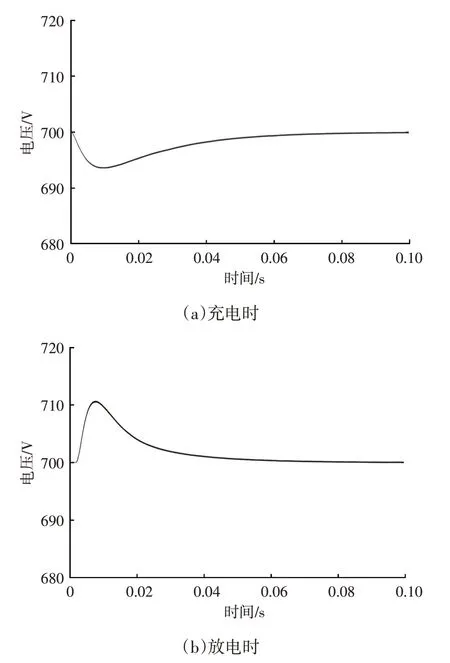
图14 充放电时直流母线电压波形

并网电流快速傅里叶变换（Fast Fourier Transform，FFT）分析结果如图15所示，并网电流THD为0.86%，小于5%，符合并网要求。

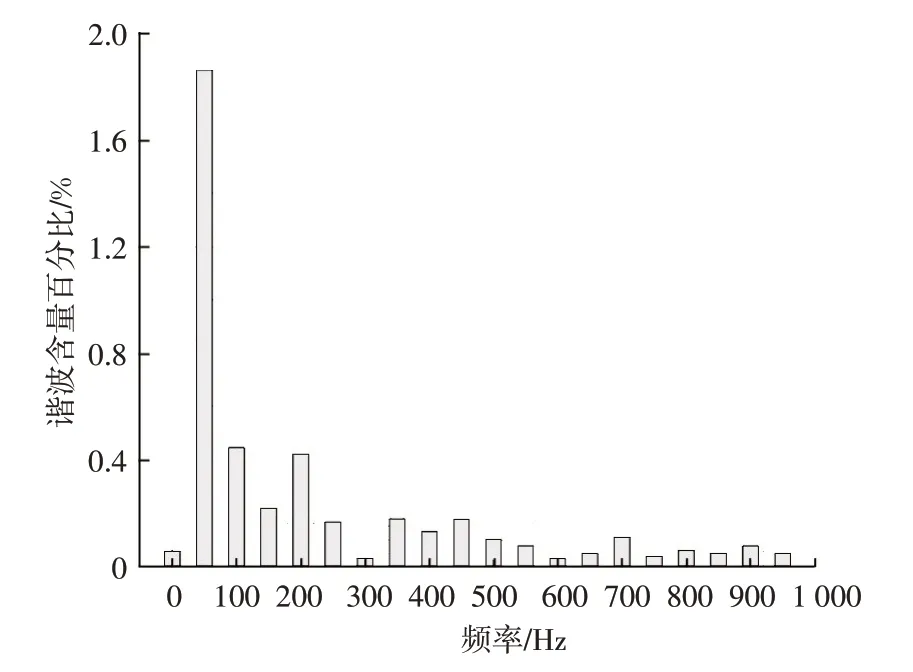
图15 并网电流THD

6 结束语

本文提出了一种用于V2G的两级式双向AC/DC 变换器，分析了其工作原理并建立数学模型，对其充放电控制策略和LCL滤波器进行设计，得到以下结论：

a.两级式双向AC/DC变换器功率器件数量少，可根据电网侧和蓄电池侧的特点独立设计控制策略，易于实现对蓄电池充放电过程的控制，延长蓄电池的使用寿命。

b.控制策略具有动态响应速度快、抗干扰性强的特点，可实现单位功率因数充放电。

c.采用SVPWM 技术，直流母线电压利用率高、谐波含量低，并网电流THD 仅为0.86%，对电网电能质量影响小。

d.LCL滤波器对高频谐波有良好的衰减特性，应用无源阻尼法可抑制其固有的谐振尖峰。

综上，本文构建的V2G 仿真模型结果验证了所提出控制策略的正确性，可实现电动汽车与电网之间能量的双向流动。